Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T19:55:26.205Z Has data issue: false hasContentIssue false
  • English
  • Français

SOLUTIONS TO DIAGONAL CONGRUENCES WITH VARIABLES RESTRICTED TO A BOX

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  03 April 2018

Todd Cochrane ,
Misty Ostergaard  and
Craig Spencer
Todd Cochrane
Affiliation:
Department of Mathematics, Kansas State University, Manhattan, KS 66506, U.S.A. email cochrane@math.ksu.edu
Misty Ostergaard
Affiliation:
Department of Mathematics, University of Southern Indiana, Evansville, IN 47712, U.S.A. email m.ostergaard@usi.edu
Craig Spencer
Affiliation:
Department of Mathematics, Kansas State University, Manhattan, KS 66506, U.S.A. email cvs@math.ksu.edu
Get access

Abstract

We prove that for any positive integers 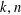$k,n$ with 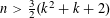$n>\frac{3}{2}(k^{2}+k+2)$, prime 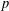$p$, and integers 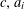$c,a_{i}$, with 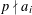$p\nmid a_{i}$, 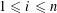$1\leqslant i\leqslant n$, there exists a solution 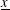$\text{}\underline{x}$ to the congruence

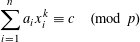$$\begin{eqnarray}\mathop{\sum }_{i=1}^{n}a_{i}x_{i}^{k}\equiv c\hspace{0.6em}({\rm mod}\hspace{0.2em}p)\end{eqnarray}$$
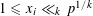with $1\leqslant {x_{i}\ll }_{k}p^{1/k}$, $1\leqslant i\leqslant n$. This upper bound is best possible. Refinements are given for smaller $n$, and for variables restricted to intervals in more general position. In particular, for any 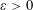$\unicode[STIX]{x1D700}>0$ we give an explicit constant $c_{\unicode[STIX]{x1D700}}$ such that if 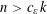$n>c_{\unicode[STIX]{x1D700}}k$, then there is a solution with 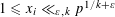$1\leqslant {x_{i}\ll }_{\unicode[STIX]{x1D700},k}p^{1/k+\unicode[STIX]{x1D700}}$.

MSC classification

Primary: 11L07: Estimates on exponential sums 11L03: Trigonometric and exponential sums, general
Type
Research Article
Information
Mathematika , Volume 64 , Issue 2 , 2018 , pp. 430 - 444
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, R. C., Small solutions of congruences. Mathematika 30 1983, 164–188.CrossRefGoogle Scholar
Baker, R. C., Diophantine Inequalities (London Mathematical Society Monographs), Clarendon Press (Oxford, 1986).Google Scholar
Bourgain, J., Demeter, C. and Guth, L., Proof of the main conjecture in Vinogradov’s mean value theorem for degrees higher than three. Ann. of Math. (2) 184(2) 2016, 633–682.Google Scholar
Cilleruelo, J., Garaev, M. Z., Ostafe, A. and Shparlinski, I. E., On the concentration of points of polynomial maps and applications. Math. Z. 272 2012, 825–837.CrossRefGoogle Scholar
Cochrane, T., Exponential Sums and the Distributions of Solutions of Congruences (Institute of Mathematics), Academia Sinica (Taipei, Taiwan, 1994), 1–84.Google Scholar
Cochrane, T., Ostergaard, M. and Spencer, C., Small solutions of diagonal congruences. Funct. Approx. Comment. Math. 56(1) 2017, 39–48.CrossRefGoogle Scholar
Cochrane, T. and Zheng, Z., Small solutions of the congruence a 1 x 1 2 + a 2 x 2 2 + a 3 x 3 2 + a 4 x 4 2 ≡ c (mod p). Acta Math. Sinica (N.S.) 14(2) 1998, 175–182.CrossRefGoogle Scholar
Dietmann, R., Small solutions of additive cubic congruences. Arch. Math. 75 2000, 195–197.CrossRefGoogle Scholar
Ramaswami, V., On the number of positive integers less than x and free of prime divisors greater than x c . Bull. Amer. Math. Soc. 55 1949, 1122–1127.CrossRefGoogle Scholar
Sárközy, A., On products and shifted products of residues modulo p. Integers 8(2) 2008, A9, 8 pp.Google Scholar
Schmidt, W. M., Small zeros of additive forms in many variables, II. Acta Math. 143(3–4) 1979, 219–232.Google Scholar
Schmidt, W. M., Bounds on exponential sums. Acta Arith. 94(3) 1984, 281–297.Google Scholar
Schmidt, W. M., Small solutions of congruences with prime modulus. In Diophantine Analysis, Proc. Number Theory Sect. Aust. Math. Soc. Conv. 1985 (London Mathematical Society Lecture Notes Series 109 ), Cambridge University Press (Cambridge, 1986), 37–66.Google Scholar
Shparlinski, I. E. and Zumalacárregui, A., On the density of zeros of diagonal forms modulo a prime. Preprint, 2017.Google Scholar
Vinogradov, I. M., New estimates for Weyl sums. Dokl. Akad. Nauk SSSR 8 1935, 195–198.Google Scholar
Wooley, T. D., New estimates for smooth Weyl sums. J. Lond. Math. Soc. 51 1995, 1–13.Google Scholar
Wooley, T. D., Vinogradov’s mean value theorem via efficient congruencing. Ann. of Math. (2) 175 2012, 1575–1627.Google Scholar
Wooley, T. D., Vinogradov’s mean value theorem via efficient congruencing, II. Duke Math. J. 162 2013, 673–730.CrossRefGoogle Scholar