Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-11T20:17:44.189Z Has data issue: false hasContentIssue false
  • English
  • Français

SET MAPPINGS WITH FREE SETS WHICH ARE ARITHMETIC PROGRESSIONS

Part of: Set theory

Published online by Cambridge University Press:  06 February 2018

Péter Komjáth
Péter Komjáth*
Affiliation:
Institute of Mathematics, Eötvös University, Budapest, Pázmány P. s. 1/C 1117, Hungary email kope@cs.elte.hu
Get access

Abstract

If 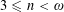$3\leqslant n<\unicode[STIX]{x1D714}$ and 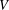$V$ is a vector space over 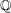$\mathbb{Q}$ with 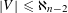$|V|\leqslant \aleph _{n-2}$, then there is a well ordering of $V$ such that every vector is the last element of only finitely many length-$n$ arithmetic progressions ($n$-APs). This implies that there is a set mapping 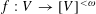$f:V\rightarrow [V]^{{<}\unicode[STIX]{x1D714}}$ with no free set which is an $n$-AP. 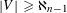If, however, $|V|\geqslant \aleph _{n-1}$, then for every set mapping 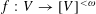$f:V\rightarrow [V]^{{<}\unicode[STIX]{x1D714}}$ there is a free set which is an $n$-AP.

MSC classification

Primary: 03E05: Other combinatorial set theory
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 71 - 76
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ceder, J., On decomposition into anticonvex sets. Rev. Roumaine Math. Pures Appl. 14 1969, 955–961.Google Scholar
Erdős, P., Problems and results in chromatic graph theory. In Proof Techniques in Graph Theory, Academic Press (New York, NY, 1969), 27–35.Google Scholar
Erdős, P. and Kakutani, S., On nondenumerable graphs. Bull. Amer. Math. Soc. 49 1943, 457–461.CrossRefGoogle Scholar
Erdős, P. and Komjáth, P., Countable decompositions of ℝ2 and ℝ3 . Discrete Comput. Geom. 5 1990, 325–331.CrossRefGoogle Scholar
Fodor, G., Proof of a conjecture of Erdős. Acta Sci. Math. (Szeged) 14 1951–1952, 219–227.Google Scholar
Hindman, N., Leader, I. and Strauss, D., Pairwise sums in colourings of the reals. Abh. Math. Semin. Univ. Hambg. 87 2017, 275–287, doi:10.1007/s12188-016-0166-x.CrossRefGoogle Scholar
Kuratowski, K., Sur une charactérisation des alephs. Fund. Math. 38 1951, 14–17.CrossRefGoogle Scholar
Sierpiński, W., Sur quelques propositions concernant la puissance du continu. Fund. Math. 38 1951, 1–13.CrossRefGoogle Scholar
Sierpiński, W., Hypothèse du Continu, 2nd edn., Chelsea Publishing Company (New York, 1956).Google Scholar