Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-06T13:09:16.977Z Has data issue: false hasContentIssue false
  • English
  • Français

MODELS OF TORSORS OVER AFFINE SPACES

Part of: Algebraic groups Arithmetic algebraic geometry

Published online by Cambridge University Press:  07 March 2019

Marco Antei  and
Jorge Esquivel Araya
Marco Antei
Affiliation:
Escuela de Matematica, Universidad de Costa Rica, Ciudad universitaria Rodrigo Facio Brenes, Costa Rica email marco.antei@ucr.ac.cr
Jorge Esquivel Araya
Affiliation:
Escuela de Matematica, Universidad de Costa Rica, Ciudad universitaria Rodrigo Facio Brenes, Costa Rica email jorge.esquivelaraya@ucr.ac.cr
Get access

Abstract

Let 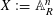$X:=\mathbb{A}_{R}^{n}$ be the $n$-dimensional affine space over a discrete valuation ring 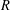$R$ with fraction field 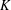$K$. We prove that any pointed torsor 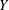$Y$ over 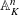$\mathbb{A}_{K}^{n}$ under the action of an affine finite-type group scheme can be extended to a torsor over 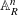$\mathbb{A}_{R}^{n}$ possibly after pulling 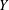$Y$ back over an automorphism of $\mathbb{A}_{K}^{n}$. The proof is effective. Other cases, including 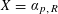$X=\unicode[STIX]{x1D6FC}_{p,R}$, are also discussed.

MSC classification

Primary: 14L30: Group actions on varieties or schemes (quotients) 14L15: Group schemes
Secondary: 11G99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 65 , Issue 3 , 2019 , pp. 530 - 541
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman, S., Schémas en groupes, espaces homogènes et espaces algébriques sur une base de dimension 1. Mém. Soc. Math. Fr. 33 1973, 5–79.Google Scholar
Antei, M., On the abelian fundamental group scheme of a family of varieties. Israel J. Math. 186 2011, 427–446.Google Scholar
Antei, M., Extension of finite solvable torsors over a curve. Manuscripta Math. 140(1) 2013, 179–194.Google Scholar
Antei, M. and Dey, A., The pseudo-fundamental group scheme. J. Algebra 523 2019, 274–284.Google Scholar
Antei, M. and Emsalem, M., Models of torsors and the fundamental group scheme. Nagoya Math. J. 230 2018, 18–34.Google Scholar
Antei, M., Emsalem, M. and Gasbarri, C., Sur l’existence du schéma en groupes fondamental. Preprint, 2015, arXiv:1504.05082v3 [math.AG].Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron Models, Springer (Berlin, Heidelberg, New York, 1980).Google Scholar
Demazure, M. and Gabriel, P., Groupes Algébriques, North-Holland (Amsterdam, 1970).Google Scholar
Grothendieck, A., Éléments de géomérie algébrique. IV. Étude locale des schémas et des morphismes de schémas. 2. Publ. Math. Inst. Hautes Études Sci. 24 1965.Google Scholar
Grothendieck, A., Revêtements étales et groupe fondamental (SGA 1), Séminaire de géométrie algébrique du Bois Marie – 1960–61 (Lecture Notes in Mathematics 224 ), Springer (Berlin, Heidelberg, New York, 1971).Google Scholar
Milne, J. S., Étale Cohomology, Princeton University Press (Princeton, NJ, 1980).Google Scholar
Milne, J. S., Arithmetic Duality Theorems (Perspectives in Mathematics 1 ), Academic Press (Boston, MA, 1986).Google Scholar
Raynaud, M., p-groupes et réduction semi-stable des courbes. In The Grothendieck Festschrift, Vol. III (Progress in Mathematics 88 ), Birkhäuser (Boston, MA, 1990), 179–197.Google Scholar
Saïdi, M., Torsors under finite and flat group schemes of rank p with Galois action. Math. Z. 245(4) 2003, 695–710.Google Scholar
Tossici, D., Effective models and extension of torsors over a d.v.r. of unequal characteristic. Int. Math. Res. Not. IMRN 2008 2008, article ID rnn111, 68 pages.Google Scholar
Waterhouse, W. C., Introduction to Affine Group Schemes (Graduate Texts in Mathematics), Springer (New York, 1979).Google Scholar
Waterhouse, W. C. and Weisfeiler, B., One-dimensional affine group schemes. J. Algebra 66 1980, 550–568.Google Scholar