Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-14T12:39:23.341Z Has data issue: false hasContentIssue false
  • English
  • Français

DISSOLVING OF CUSP FORMS: HIGHER-ORDER FERMI’S GOLDEN RULES

Part of: Discontinuous groups and automorphic forms Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press:  21 January 2013

Yiannis N. Petridis  and
Morten S. Risager
Yiannis N. Petridis
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, U.K. (email: i.petridis@ucl.ac.uk)
Morten S. Risager
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen Ø, Denmark (email: risager@math.ku.dk)
Get access

Abstract

For a hyperbolic surface, embedded eigenvalues of the Laplace operator are unstable and tend to dissolve into scattering poles i.e. become resonances. A sufficient dissolving condition was identified by Phillips–Sarnak and is elegantly expressed in Fermi’s golden rule. We prove formulas for higher approximations and obtain necessary and sufficient conditions for dissolving a cusp form with eigenfunction $u_j$ into a resonance. In the framework of perturbations in character varieties, we relate the result to the special values of the $L$-series 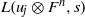$L(u_j\otimes F^n, s)$. This is the Rankin–Selberg convolution of $u_j$ with 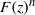$F(z)^n$, where 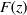$F(z)$is the antiderivative of a weight two cusp form. In an example we show that the above-mentioned conditions force the embedded eigenvalue to become a resonance in a punctured neighborhood of the deformation space.

MSC classification

Secondary: 11F72: Spectral theory; Selberg trace formula 58J50: Spectral problems; spectral geometry; scattering theory
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 269 - 301
Copyright
Copyright © 2013 University College London 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Avelin, H., Deformation of $\Gamma _0(5)$-cusp forms. Math. Comp. 76(257) (2007), 361–384.CrossRefGoogle Scholar
[2]Balslev, E., Spectral deformation of Laplacians on hyperbolic manifolds. Comm. Anal. Geom. 5(2) (1997), 213–247.CrossRefGoogle Scholar
[3]Balslev, E. and Venkov, A., Spectral theory of Laplacians for Hecke groups with primitive character. Acta Math. 186(2) (2001), 155–217.CrossRefGoogle Scholar
[4]Balslev, E. and Venkov, A., On the relative distribution of eigenvalues of exceptional Hecke operators and automorphic Laplacians. Algebra i Analiz 17(1) (2005), 5–52, translation in St. Petersburg Math. J. 17(1) (2006), 1–37.Google Scholar
[5]Bruggeman, R.W., Families of Automorphic Forms (Monographs in Mathematics 88), Birkhäuser Boston, Inc. (Boston, MA, 1994).CrossRefGoogle Scholar
[6]Chinta, G. and Goldfeld, D., Grössencharakter $L$-functions of real quadratic fields twisted by modular symbols. Invent. Math. 144(3) (2001), 435–449.CrossRefGoogle Scholar
[7]Deitmar, A. and Diamantis, N., Automorphic forms of higher order. J. Lond. Math. Soc. (2) 80(1) (2009), 18–34.CrossRefGoogle Scholar
[8]Diamantis, N., Knopp, M., Mason, M. and O’Sullivan, C., $L$-functions of second-order cusp forms. Ramanujan J. 12(3) (2006), 327–347.CrossRefGoogle Scholar
[9]Colin de Verdière, Y., Pseudo-laplaciens II. Ann. Inst. Fourier (Grenoble) 33(2) (1983), 87–113.CrossRefGoogle Scholar
[10]Deshouillers, J.-M. and Iwaniec, H., The nonvanishing of Rankin–Selberg zeta-functions at special points. In The Selberg Trace Formula and Related Topics (Brunswick, Maine, 1984) (Contemporary Mathematics 53), American Mathematical Society (Providence, RI, 1986), 51–95.CrossRefGoogle Scholar
[11]Deshouillers, J.-M., Iwaniec, H., Phillips, R. S. and Sarnak, P., Maass cusp forms. Proc. Nat. Acad. Sci. USA 82(11) (1985), 3533–3534.CrossRefGoogle ScholarPubMed
[12]Diamantis, N. and O’Sullivan, C., Hecke theory of series formed with modular symbols and relations among convolution $L$-functions. Math. Ann. 318(1) (2000), 85–105.CrossRefGoogle Scholar
[13]Elkies, Noam D., Elliptic and modular curves over finite fields and related computational issues.In Computational Perspectives on Number Theory (Chicago, IL, 1995) (AMS/IP Studies in Advanced Mathematics 7), American Mathematical Society (Providence, RI, 1998), 21–76.Google Scholar
[14]Farmer, D. and Lemurell, S., Deformations of Maass forms. Math. Comput. 74 (2005), 1967–1982.CrossRefGoogle Scholar
[15]Goldfeld, D., Zeta functions formed with modular symbols. In Automorphic Forms, Automorphic Representations, and Arithmetic (Fort Worth, TX, 1996) (Proceedings of Symposia in Pure Mathematics 66, Part 1), American Mathematical Society (Providence, RI, 1999), 111–121.CrossRefGoogle Scholar
[16]Goldfeld, D., The distribution of modular symbols. In Number Theory in Progress, Vol. 2 (Zakopane-Kościelisko, 1997), de Gruyter (Berlin, 1999), 849–865.CrossRefGoogle Scholar
[17]Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series, and Products, 7th edn, Elsevier/Academic Press (Amsterdam, 2007).Google Scholar
[18]Hejhal, D. A., The Selberg Trace Formula for PSL(2, R), Vol. 2 (Lecture Notes in Mathematics 1001), Springer-Verlag (Berlin, 1983).CrossRefGoogle Scholar
[19]Iwaniec, H., Spectral Methods of Automorphic Forms, 2nd edn (Graduate Studies in Mathematics 53), American Mathematical Society (Providence, RI, 2002); Revista Matematica Iberoamericana, Madrid, 2002.CrossRefGoogle Scholar
[20]Jorgenson, J. and O’Sullivan, C., Unipotent vector bundles and higher-order non-holomorphic Eisenstein series. J. Théor. Nombres Bordeaux 20(1) (2008), 131–163.CrossRefGoogle Scholar
[21]Kato, T., Perturbation Theory for Linear Operators, Reprint of the 1980 edition (Classics in Mathematics), Springer-Verlag (Berlin, 1995).CrossRefGoogle Scholar
[22]Lax, P. D. and Phillips, R. S., Scattering Theory for Automorphic Functions (Annals of Mathematics Studies 87), Princeton University Press (Princeton, NJ, 1976).Google Scholar
[23]Luo, W., Nonvanishing of $L$-values and the Weyl law. Ann. of Math. (2) 154(2) (2001), 477–502.CrossRefGoogle Scholar
[24]Mazur, B. and Swinnerton-Dyer, P., Arithmetic of Weil curves. Invent. Math. 25 (1974), 1–61.CrossRefGoogle Scholar
[25]Müller, W., Spectral theory for Riemannian manifolds with cusps and a related trace formula. Math. Nachr. 111 (1983), 197–288.CrossRefGoogle Scholar
[26]Müller, W., Spectral geometry and scattering theory for certain complete surfaces of finite volume. Invent. Math. 109(2) (1992), 265–305.CrossRefGoogle Scholar
[27]Müller, W., On the analytic continuation of rank one Eisenstein series. Geom. Funct. Anal. 6(3) (1996), 572–586.CrossRefGoogle Scholar
[28]O’Sullivan, C., Properties of Eisenstein series formed with modular symbols. PhD Thesis, Columbia University, 1998.Google Scholar
[29]O’Sullivan, C., Properties of Eisenstein series formed with modular symbols. J. Reine Angew. Math. 518 (2000), 163–186.Google Scholar
[30]Petridis, Y. N., On the singular set, the resolvent and Fermi’s golden rule for finite volume hyperbolic surfaces. Manuscripta Math. 82(3–4) (1994), 331–347.CrossRefGoogle Scholar
[31]Petridis, Y. N., Spectral deformations and Eisenstein series associated with modular symbols. Internat. Math. Res. Notices (19) (2002), 991–1006.CrossRefGoogle Scholar
[32]Petridis, Y. N. and Risager, M. S., Modular symbols have a normal distribution. Geom. Funct. Anal. 14(5) (2004), 1013–1043.CrossRefGoogle Scholar
[33]Petridis, Y. N. and Risager, M. S., Dissolving cusp forms in Teichmüller spaces (in preparation).Google Scholar
[34]Phillips, R. S. and Sarnak, P., On cusp forms for co-finite subgroups of ${\rm PSL}(2,R)$. Invent. Math. 80(2) (1985), 339–364.CrossRefGoogle Scholar
[35]Phillips, R. and Sarnak, P., Perturbation theory for the Laplacian on automorphic functions. J. Amer. Math. Soc. 5(1) (1992), 1–32.CrossRefGoogle Scholar
[36]Phillips, R. and Sarnak, P., Cusp forms for character varieties. Geom. Funct. Anal. 4(1) (1994), 93–118.CrossRefGoogle Scholar
[37]Risager, M., Automorphic forms and modular symbols. PhD Thesis, Aarhus Universitet, 2003.Google Scholar
[38]Sarnak, P., On cusp forms. II. In Festschrift in Honor of I. I. Piatetski-Shapiro on the Occasion of his Sixtieth Birthday, Part II (Ramat Aviv, 1989) (Israel Mathematical Conference Proceedings 3), Weizmann (Jerusalem, 1990), 237–250.Google Scholar
[39]Selberg, A., Göttingen Lecture Notes in Collected Papers, with a foreword by K. Chandrasekharan Vol. I, Springer-Verlag (Berlin, 1989).Google Scholar
[40]Simon, B., Resonances in $n$-body quantum systems with dilatation analytic potentials and the foundations of time-dependent perturbation theory. Ann. of Math. (2) 97 (1973), 247–274.CrossRefGoogle Scholar
[41]Strömberg, F., Computational aspects of maass waveform. PhD Thesis, University of Uppsala, 2005.Google Scholar
[42]Wolpert, S. A., Disappearance of cusp forms in special families. Ann. of Math. (2) 139(2) (1994), 239–291.CrossRefGoogle Scholar