No CrossRef data available.
Published online by Cambridge University Press: 23 April 2018
Let  $s\geqslant 3$ be a fixed positive integer and let
$s\geqslant 3$ be a fixed positive integer and let 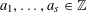 $a_{1},\ldots ,a_{s}\in \mathbb{Z}$ be arbitrary. We show that, on average over
$a_{1},\ldots ,a_{s}\in \mathbb{Z}$ be arbitrary. We show that, on average over 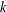 $k$, the density of numbers represented by the degree
$k$, the density of numbers represented by the degree 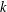 $k$ diagonal form decays rapidly with respect to
$k$ diagonal form decays rapidly with respect to  $$\begin{eqnarray}a_{1}x_{1}^{k}+\cdots +a_{s}x_{s}^{k}\end{eqnarray}$$
$$\begin{eqnarray}a_{1}x_{1}^{k}+\cdots +a_{s}x_{s}^{k}\end{eqnarray}$$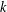 $k$.
$k$.