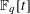Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T14:24:30.549Z Has data issue: false hasContentIssue false
  • English
  • Français

LINEAR AND QUADRATIC UNIFORMITY OF THE MÖBIUS FUNCTION OVER $\mathbb{F}_{q}[t]$

Part of: Finite fields and commutative rings (number-theoretic aspects) Sequences and sets

Published online by Cambridge University Press:  05 March 2019

Pierre-Yves Bienvenu  and
Thái Hoàng Lê
Pierre-Yves Bienvenu
Affiliation:
Institut Camille-Jordan, Université Lyon 1, 43 boulevard du 11 novembre 1918, 69622 Villeurbanne cedex, France email pbienvenu@math.univ-lyon1.fr
Thái Hoàng Lê
Affiliation:
Department of Mathematics, The University of Mississippi, University, MS 38677, U.S.A. email leth@olemiss.edu
Get access

Abstract

We examine correlations of the Möbius function over 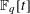$\mathbb{F}_{q}[t]$ with linear or quadratic phases, that is, averages of the form 1

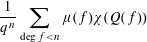$$\begin{eqnarray}\frac{1}{q^{n}}\mathop{\sum }_{\deg f<n}\unicode[STIX]{x1D707}(f)\unicode[STIX]{x1D712}(Q(f))\end{eqnarray}$$
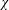for an additive character $\unicode[STIX]{x1D712}$ over 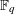$\mathbb{F}_{q}$ and a polynomial $Q\in \mathbb{F}_{q}[x_{0},\ldots ,x_{n-1}]$ of degree at most 2 in the coefficients 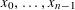$x_{0},\ldots ,x_{n-1}$ of 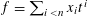$f=\sum _{i<n}x_{i}t^{i}$. As in the integers, it is reasonable to expect that, due to the random-like behaviour of 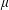$\unicode[STIX]{x1D707}$, such sums should exhibit considerable cancellation. 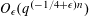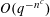In this paper we show that the correlation (1) is bounded by $O_{\unicode[STIX]{x1D716}}(q^{(-1/4+\unicode[STIX]{x1D716})n})$ for any $\unicode[STIX]{x1D716}>0$ if $Q$ is linear and $O(q^{-n^{c}})$ for some absolute constant 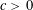$c>0$ if $Q$ is quadratic. 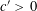The latter bound may be reduced to $O(q^{-c^{\prime }n})$ for some $c^{\prime }>0$ when 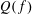$Q(f)$ is a linear form in the coefficients of 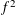$f^{2}$, that is, a Hankel quadratic form, whereas, for general quadratic forms, it relies on a bilinear version of the additive-combinatorial Bogolyubov theorem.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 11T55: Arithmetic theory of polynomial rings over finite fields
Type
Research Article
Information
Mathematika , Volume 65 , Issue 3 , 2019 , pp. 505 - 529
Copyright
Copyright © University College London 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, R. C. and Harman, G., Exponential sums formed with the Möbius function. J. Lond. Math. Soc. (2) 43(2) 1991, 193–198.Google Scholar
Bhowmick, A., Lê, T. H. and Liu, Y.-R., A note on character sums in finite fields. Finite Fields Appl. 46 2017, 247–254.Google Scholar
Bienvenu, P.-Y. and Lê, T. H., A bilinear Bogolyubov theorem. European J. Combin. 77 2019, 102–113.Google Scholar
Car, M., Distribution des polynômes irréductibles dans F q [T]. Acta Arith. 88(2) 1999, 141–153.Google Scholar
Davenport, H., On some infinite series involving arithmetical functions. Q. J. Math. 8 1937, 8–13.Google Scholar
Green, B. and Tao, T., An inverse theorem for the Gowers U 3(G) norm. Proc. Edinb. Math. Soc. (2) 51(1) 2008, 73–153.Google Scholar
Green, B. and Tao, T., Quadratic uniformity of the Möbius function. Ann. Inst. Fourier (Grenoble) 58(6) 2008, 1863–1935.Google Scholar
Green, B. and Tao, T., The Möbius function is strongly orthogonal to nilsequences. Ann. of Math. (2) 175(2) 2012, 541–566.Google Scholar
Hayes, D. R., The distribution of irreducibles in GF[q, x]. Trans. Amer. Math. Soc. 117 1965, 101–127.Google Scholar
He, X. and Huang, B., Exponential sums involving the Möbius function. Acta Arith. 175(3) 2016, 201–209.Google Scholar
Hosseini, K. and Lovett, S., A bilinear Bogolyubov–Ruzsa lemma with poly-logarithmic bounds. Preprint, 2018, arXiv:1808:049651.Google Scholar
Hsu, C.-N., The distribution of irreducible polynomials in F q [t]. J. Number Theory 61 1996, 85–96.Google Scholar
Lê, T. H., Green–Tao theorem in function fields. Acta Arith. 147 2011, 129–152.Google Scholar
Liu, Y.-R. and Wooley, T. D., Waring’s problem in function fields. J. reine angew. Math. 638 2010, 1–67.Google Scholar
Porritt, S., A note on exponential-Möbius sums over F q [t]. Finite Fields Appl. 51 2018, 298–305.Google Scholar
Rhin, G., Répartition modulo 1 dans un corps de séries formelles sur un corps fini. Dissertationes Math. (Rozprawy Mat.) 95 1972, 75 pp.Google Scholar
Samorodnitsky, A., Low-degree tests at large distances. In STOC’07—Proc. 39th Annu. ACM Symp. Theory of Computing, ACM (New York, 2007), 506–515.Google Scholar
Sanders, T., On the Bogolyubov–Ruzsa lemma. Anal. PDE 5(3) 2012, 627–655.Google Scholar
Tao, T. and Ziegler, T., The inverse conjecture for the Gowers norm over finite fields via the correspondence principle. Anal. PDE 3(1) 2010, 1–20.Google Scholar
Zhan, T. and Liu, J.-Y., Exponential sums involving the Möbius function. Indag. Math. (N.S.) 7(2) 1996, 271–278.Google Scholar