Hostname: page-component-6bf8c574d5-rwnhh Total loading time: 0 Render date: 2025-02-22T12:09:35.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Finitary 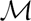$\mathcal{M}$-adhesive categories

Published online by Cambridge University Press:  26 June 2014

KARSTEN GABRIEL ,
BENJAMIN BRAATZ ,
HARTMUT EHRIG  and
ULRIKE GOLAS
KARSTEN GABRIEL
Affiliation:
Technische Universität Berlin, Berlin, Germany Email: kgabriel@cs.tu-berlin.de
BENJAMIN BRAATZ
Affiliation:
Université du Luxembourg, Luxembourg Email: benjamin.braatz@uni.lu
HARTMUT EHRIG
Affiliation:
Technische Universität Berlin, Berlin, Germany Email: ehrig@cs.tu-berlin.de
ULRIKE GOLAS
Affiliation:
Konrad-Zuse-Zentrum für Informationstechnik Berlin, Berlin, Germany Email: golas@zib.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Finitary 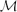$\mathcal{M}$-adhesive categories are 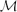$\mathcal{M}$-adhesive categories with finite objects only, where 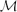$\mathcal{M}$-adhesive categories are a slight generalisation of weak adhesive high-level replacement (HLR) categories. We say an object is finite if it has a finite number of 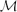$\mathcal{M}$-subobjects. In this paper, we show that in finitary 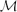$\mathcal{M}$-adhesive categories we not only have all the well-known HLR properties of weak adhesive HLR categories, which are already valid for 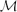$\mathcal{M}$-adhesive categories, but also all the additional HLR requirements needed to prove classical results including the Local Church-Rosser, Parallelism, Concurrency, Embedding, Extension and Local Confluence Theorems, where the last of these is based on critical pairs. More precisely, we are able to show that finitary 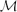$\mathcal{M}$-adhesive categories have a unique 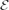$\mathcal{E}$-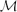$\mathcal{M}$ factorisation and initial pushouts, and the existence of an 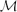$\mathcal{M}$-initial object implies we also have finite coproducts and a unique 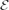$\mathcal{E}$′-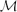$\mathcal{M}$ pair factorisation. Moreover, we can show that the finitary restriction of each 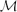$\mathcal{M}$-adhesive category is a finitary 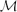$\mathcal{M}$-adhesive category, and finitarity is preserved under functor and comma category constructions based on 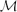$\mathcal{M}$-adhesive categories. This means that all the classical results are also valid for corresponding finitary 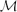$\mathcal{M}$-adhesive transformation systems including several kinds of finitary graph and Petri net transformation systems. Finally, we discuss how some of the results can be extended to non-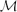$\mathcal{M}$-adhesive categories.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 24 , Issue 4: Structure Transformation , August 2014 , 240403
Copyright
Copyright © Cambridge University Press 2014 

References

Adámek, J., Herrlich, H. and Strecker, G. (1990) Abstract and Concrete Categories, Wiley.Google Scholar
Baldan, P., Bonchi, F., Corradini, A., Heindel, T. and König, B. (2011) A Lattice-Theoretical Perspective on Adhesive Categories. Journal of Symbolic Computation 46 222–245.CrossRefGoogle Scholar
Baldan, P., Bonchi, F., Heindel, T. and König, B. (2008) Irreducible Objects and Lattice Homomorphisms in Adhesive Categories. In: Pfalzgraf, J. (ed.) Proceedings of ACCAT '08 (Workshop on Applied and Computational Category Theory).Google Scholar
Braatz, B. (2009) Formal Modelling and Application of Graph Transformations in the Resource Description Framework, Dissertation, Technische Universität Berlin.Google Scholar
Braatz, B. and Brandt, C. (2008) Graph transformations for the Resource Description Framework. In: Ermel, C., Heckel, R. and de Lara, J. (eds.) Proceedings GT-VMT 2008. Electronic Communications of the EASST 10.Google Scholar
Braatz, B., Ehrig, H., Gabriel, K. and Golas, U. (2010) Finitary $\mathcal{M}$-Adhesive Categories. In: Proceedings ICGT 2010. Springer-Verlag Lecture Notes in Computer Science 6372 234–249.CrossRefGoogle Scholar
Braatz, B., Golas, U. and Soboll, T. (2011) How to delete categorically – two pushout complement constructions. Journal of Symbolic Computation 46 246–271.CrossRefGoogle Scholar
Cockett, J. R. B. and Lack, S. (2002) Restriction categories I: categories of partial maps. Theoretical Computer Science 270 (1–2)223–259.CrossRefGoogle Scholar
Corradini, A., Heindel, T., Hermann, F. and König, B. (2006) Sesqui-Pushout Rewriting. In: Corradini, A., Ehrig, H., Montanari, U., Ribeiro, L. and Rozenberg, G. (eds.) Proceedings of ICGT 2006. Springer-Verlag Lecture Notes in Computer Science 4178 30–45.CrossRefGoogle Scholar
Ehrig, H. (1979) Introduction to the Algebraic Theory of Graph Grammars (A Survey). In: Claus, V., Ehrig, H. and Rozenberg, G. (eds.) Graph Grammars and their Application to Computer Science and Biology. Springer-Verlag Lecture Notes in Computer Science 73 1–69.CrossRefGoogle Scholar
Ehrig, H., Ehrig, K., Prange, U. and Taentzer, G. (2006a) Fundamentals of Algebraic Graph Transformation, EATCS Monographs, Springer-Verlag.Google Scholar
Ehrig, H., Golas, U. and Hermann, F. (2010) Categorical Frameworks for Graph Transformations and HLR Systems based on the DPO Approach. Bulletin of the EATCS 102 111–121.Google Scholar
Ehrig, H., Padberg, J., Prange, U. and Habel, A. (2006b) Adhesive High-Level Replacement Systems: A New Categorical Framework for Graph Transformation. Fundamenta Informaticae 74 (1)1–29.Google Scholar
Habel, A. and Pennemann, K.-H. (2009) Correctness of High-Level Transformation Systems Relative to Nested Conditions. Mathematical Structures in Computer Science 19 (2)245–296.CrossRefGoogle Scholar
Heckel, R., Ehrig, H., Wolter, U. and Corradini, A. (2001) Double-pullback transitions and coalgebraic loose semantics for graph transformation systems. Applied Categorical Structures 9 (1)83–110.CrossRefGoogle Scholar
Heindel, T. (2010) Hereditary Pushouts Reconsidered. In: Proceedings ICGT 2010. Springer-Verlag Lecture Notes in Computer Science 6372 250–265.CrossRefGoogle Scholar
Klyne, G. and Carroll, J. J. (2004) Resource Description Framework (RDF): Concepts and Abstract Syntax, World Wide Web Consortium (W3C). Available at http://www.w3.org/TR/2004/REC-rdf-concepts-20040210/.Google Scholar
Lack, S. and Sobociński, P. (2004) Adhesive Categories. In: Walukiewicz, I. (ed.) Proceedings FOSSACS 2004. Springer-Verlag Lecture Notes in Computer Science 2987 273–288.CrossRefGoogle Scholar
Lack, S. and Sobociński, P. (2005) Adhesive and Quasiadhesive Categories. Theoretical Informatics and Applications 39 (2)511–546.CrossRefGoogle Scholar
Löwe, M. (2010) Graph Rewriting in Span-Categories. In: Proceedings ICGT 2010. Springer-Verlag Lecture Notes in Computer Science 6372 218–233.CrossRefGoogle Scholar
Löwe, M. and Ehrig, H. (1990) Algebraic Approach to Graph Transformation Based on Single Pushout Derivations. In: Möhrung, R. (ed.) Proceedings Graph-Theoretic Concepts in Computer Science. Springer-Verlag Lecture Notes in Computer Science 484 338–353.CrossRefGoogle Scholar
MacLane, S. (1971) Categories for the Working Mathematician, Graduate Texts in Mathematics 5, Springer-Verlag.CrossRefGoogle Scholar
Modica, T.et al. (2010) Low- and High-Level Petri Nets with Individual Tokens. Technical Report 2009/13, Technische Universität Berlin. Available at http://www.eecs.tu-berlin.de/menue/forschung/forschungsberichte/2009.Google Scholar
Prange, U., Ehrig, H. and Lambers, L. (2008) Construction and Properties of Adhesive and Weak Adhesive High-Level Replacement Categories. Applied Categorical Structures 16 (3)365–388.CrossRefGoogle Scholar
Rozenberg, G. (ed.) (1997) Handbook of Graph Grammars and Computing by Graph Transformation 1: Foundations, World Scientific.CrossRefGoogle Scholar