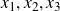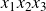1. Introduction
1·1 Quadratic forms and theta series
A positive integral
![]() $m{\times}m$
matrix Q with even diagonal entries gives rise to a quadratic form
$m{\times}m$
matrix Q with even diagonal entries gives rise to a quadratic form
![]() $q(x)= x^T Q x/2$
. It is one of the classical tasks of number theory to study which numbers n are represented by q or more precisely to count the number of solutions
$q(x)= x^T Q x/2$
. It is one of the classical tasks of number theory to study which numbers n are represented by q or more precisely to count the number of solutions
Naturally, a necessary condition for
![]() $r(Q,n) \ge 1$
is that n is locally represented by q meaning that for every prime p there exists a p-adic solution
$r(Q,n) \ge 1$
is that n is locally represented by q meaning that for every prime p there exists a p-adic solution
![]() $x_p \in ({\mathbb Z}_p)^m$
of
$x_p \in ({\mathbb Z}_p)^m$
of
![]() ${n= q(x_p)}$
. By applying the Hardy–Littlewood method, Tartakowski [Reference Tartakowsky28] showed in 1929 that for
${n= q(x_p)}$
. By applying the Hardy–Littlewood method, Tartakowski [Reference Tartakowsky28] showed in 1929 that for
![]() $m \geq 5$
every locally represented, sufficiently large n satisfies
$m \geq 5$
every locally represented, sufficiently large n satisfies
![]() ${r(Q,n) \ge 1}$
. Furthermore, he extended this result to
${r(Q,n) \ge 1}$
. Furthermore, he extended this result to
![]() $m=4$
by assuming that n is primitively locally represented which means that for every prime there is a local solution
$m=4$
by assuming that n is primitively locally represented which means that for every prime there is a local solution
![]() $x_p$
such that at least one entry of
$x_p$
such that at least one entry of
![]() $x_p$
is a unit in
$x_p$
is a unit in
![]() ${\mathbb Z}_p$
.
${\mathbb Z}_p$
.
To apply this result in practice, one needs an effective version stating how large n has to be with respect to Q. For
![]() $m \ge 5$
various effective bounds were obtained by analytical methods, see for example Watson [Reference Watson31], Hsia and Icaza [Reference Hsia and Icaza16] and Browning and Dietmann [Reference Browning and Dietmann6] and the references therein. However, these methods fail to provide satisfying results for
$m \ge 5$
various effective bounds were obtained by analytical methods, see for example Watson [Reference Watson31], Hsia and Icaza [Reference Hsia and Icaza16] and Browning and Dietmann [Reference Browning and Dietmann6] and the references therein. However, these methods fail to provide satisfying results for
![]() $m=4$
or
$m=4$
or
![]() $m=3$
, and one employs the theory of modular forms and theta series instead, as done by Blomer [Reference Blomer1], Duke [Reference Duke11], Hanke [Reference Hanke15], Rouse [Reference Rouse23] or Schulze–Pillot [Reference Schulze–Pillot25].
$m=3$
, and one employs the theory of modular forms and theta series instead, as done by Blomer [Reference Blomer1], Duke [Reference Duke11], Hanke [Reference Hanke15], Rouse [Reference Rouse23] or Schulze–Pillot [Reference Schulze–Pillot25].
To follow this latter approach, one considers
which is a modular form of weight
![]() ${m}/{2}$
with respect to
${m}/{2}$
with respect to
 \begin{equation*}\Gamma_0(N) = \Big\{ \begin{pmatrix}a &\quad b \\ \\[-7pt] c &\quad d\end{pmatrix} \in \textrm{SL}_2({\mathbb Z}) \mid c \equiv 0 \,(\textrm{mod}\ N)\Big\},\end{equation*}
\begin{equation*}\Gamma_0(N) = \Big\{ \begin{pmatrix}a &\quad b \\ \\[-7pt] c &\quad d\end{pmatrix} \in \textrm{SL}_2({\mathbb Z}) \mid c \equiv 0 \,(\textrm{mod}\ N)\Big\},\end{equation*}
where N is the level of Q, i.e. the smallest integer such that
![]() $NQ^{-1}$
is integral with even diagonal entries, and
$NQ^{-1}$
is integral with even diagonal entries, and
![]() $\chi$
is a quadratic character modulo N. The idea is to approximate
$\chi$
is a quadratic character modulo N. The idea is to approximate
![]() $\theta(Q,z)$
by a weighted average over the classes in the genus of Q. The resulting form
$\theta(Q,z)$
by a weighted average over the classes in the genus of Q. The resulting form
![]() $\theta(\textrm{gen}\ Q,n)$
is an Eisenstein series and its Fourier coefficients can be explicitly computed by
$\theta(\textrm{gen}\ Q,n)$
is an Eisenstein series and its Fourier coefficients can be explicitly computed by
 \begin{align} r(\textrm{gen}\ Q,n) = \frac{(2 \pi)^\frac{m}{2} n^{\frac{m}{2}-1} }{\Gamma(\frac{m}{2}) \sqrt{\det Q}} \prod_{p} \beta_p(n,Q),\end{align}
\begin{align} r(\textrm{gen}\ Q,n) = \frac{(2 \pi)^\frac{m}{2} n^{\frac{m}{2}-1} }{\Gamma(\frac{m}{2}) \sqrt{\det Q}} \prod_{p} \beta_p(n,Q),\end{align}
where
The p-adic densities
![]() $\beta_p(n,Q)$
contain information from the local restrictions. For
$\beta_p(n,Q)$
contain information from the local restrictions. For
![]() $m \geq 4$
and n primitively locally represented one can show that they satisfy
$m \geq 4$
and n primitively locally represented one can show that they satisfy
![]() ${\prod_p \beta_p(n,Q) \gg (n,N)^{-\delta} (nN)^{-{\epsilon}}}$
, where
${\prod_p \beta_p(n,Q) \gg (n,N)^{-\delta} (nN)^{-{\epsilon}}}$
, where
![]() ${\delta = 1/{2}}$
for
${\delta = 1/{2}}$
for
![]() $m=4$
and
$m=4$
and
![]() $\delta =1 $
for
$\delta =1 $
for
![]() $m \ge 5$
, cf. Lemma 8.
$m \ge 5$
, cf. Lemma 8.
The difference
![]() $f(z) = \theta(Q,z)- \theta(\textrm{gen}\ Q,z)= \sum_n a(n)e(nz)$
is a cusp form. To obtain an uniform upper bound for a(n), we apply the Petersson formula and proceed as in [Reference Iwaniec and Kowalski18, corollary 14·24]. This estimate also works for half-integral weights, cf. [Reference Iwaniec17, p. 389], with the only difference that we apply [Reference Waibel30, lemma 4] to bound the twisted Kloosterman sums. As a consequence, we obtain for
$f(z) = \theta(Q,z)- \theta(\textrm{gen}\ Q,z)= \sum_n a(n)e(nz)$
is a cusp form. To obtain an uniform upper bound for a(n), we apply the Petersson formula and proceed as in [Reference Iwaniec and Kowalski18, corollary 14·24]. This estimate also works for half-integral weights, cf. [Reference Iwaniec17, p. 389], with the only difference that we apply [Reference Waibel30, lemma 4] to bound the twisted Kloosterman sums. As a consequence, we obtain for
![]() $m \geq 4$
that
$m \geq 4$
that
 \begin{align} a(n) \ll {f} \, n^{\frac{m}{4}-\frac{1}{2}} \left(1+ \frac{n^{\frac{1}{4}} (n,N)^{\frac{1}{4}}} {N^{\frac{1}{2}}}\right) (nN)^{\epsilon}\end{align}
\begin{align} a(n) \ll {f} \, n^{\frac{m}{4}-\frac{1}{2}} \left(1+ \frac{n^{\frac{1}{4}} (n,N)^{\frac{1}{4}}} {N^{\frac{1}{2}}}\right) (nN)^{\epsilon}\end{align}
where the norm is induced by the inner product
The case
![]() $m=3$
is more fragile due to the existence of certain cusp forms, so called theta functions, whose non-vanishing Fourier coefficients are of the same size as
$m=3$
is more fragile due to the existence of certain cusp forms, so called theta functions, whose non-vanishing Fourier coefficients are of the same size as
![]() $r(\textrm{gen}\ Q,n)$
. To circumvent this problem, one approximates
$r(\textrm{gen}\ Q,n)$
. To circumvent this problem, one approximates
![]() $\theta(Q,z)$
by another Eisenstein series
$\theta(Q,z)$
by another Eisenstein series
![]() $\theta(\textrm{spin}\ Q,n)$
given as a weighted average over the classes in the spinor genus of Q. Then, the Fourier coefficients of
$\theta(\textrm{spin}\ Q,n)$
given as a weighted average over the classes in the spinor genus of Q. Then, the Fourier coefficients of
![]() $\theta(Q,z) - \theta(\textrm{spin}\ Q,n)$
can be estimated by a method of Duke and Iwaniec, which involves the Shimura lift, the Kuznetsov formula and an elaborate estimate for sums over Kloosterman sums. To apply the resulting bound, [Reference Waibel30, theorem 1], one employs a local argument by Blomer [Reference Blomer2, (1·7)] which shows that it is sufficient to bound
$\theta(Q,z) - \theta(\textrm{spin}\ Q,n)$
can be estimated by a method of Duke and Iwaniec, which involves the Shimura lift, the Kuznetsov formula and an elaborate estimate for sums over Kloosterman sums. To apply the resulting bound, [Reference Waibel30, theorem 1], one employs a local argument by Blomer [Reference Blomer2, (1·7)] which shows that it is sufficient to bound
![]() $r(Q,n) - r(Q',n)$
for Q, Q
$r(Q,n) - r(Q',n)$
for Q, Q
![]() $^{\prime}$
in the same spinor genus and (n, N) small. In many cases,
$^{\prime}$
in the same spinor genus and (n, N) small. In many cases,
![]() $r(\textrm{gen}\ Q,n)$
and
$r(\textrm{gen}\ Q,n)$
and
![]() $r(\textrm{spn}\ Q,n)$
coincide, and one obtains an asymptotic formula for r(Q, n).
$r(\textrm{spn}\ Q,n)$
coincide, and one obtains an asymptotic formula for r(Q, n).
1·2 Bounds for norms of theta series
The aim of this paper is to give strong uniform bounds for the inner products of
where Q, Q
![]() $^{\prime}$
are in the same genus. By definition of
$^{\prime}$
are in the same genus. By definition of
![]() $\theta(\textrm{gen}\ Q,z)$
any bound for
$\theta(\textrm{gen}\ Q,z)$
any bound for
![]() $\langle g,g \rangle$
is automatically a bound for
$\langle g,g \rangle$
is automatically a bound for
![]() $\langle \,f,f \rangle$
. Furthermore, we assume that Q is primitive meaning that the common divisor of all entries is 1.
$\langle \,f,f \rangle$
. Furthermore, we assume that Q is primitive meaning that the common divisor of all entries is 1.
The first bounds for
![]() $\langle \,f,f \rangle$
were only established in the 1990’s by Fomenko [Reference Fomenko12] and Schulze–Pillot [Reference Schulze–Pillot25] for
$\langle \,f,f \rangle$
were only established in the 1990’s by Fomenko [Reference Fomenko12] and Schulze–Pillot [Reference Schulze–Pillot25] for
![]() $m=4$
. Stronger and more general estimates were proven by Blomer in his articles about ternary quadratic forms, [Reference Blomer1] and [Reference Blomer2]. There, he shows for
$m=4$
. Stronger and more general estimates were proven by Blomer in his articles about ternary quadratic forms, [Reference Blomer1] and [Reference Blomer2]. There, he shows for
![]() $m = 3$
that
$m = 3$
that
where the latter bound is only valid for diagonal Q with smallest entry a. For
![]() $m \ge 4$
, Blomer obtains in the appendix of [Reference Sardari24] that
$m \ge 4$
, Blomer obtains in the appendix of [Reference Sardari24] that
In the special case that
![]() $\det Q$
is a fundamental discriminant, Rouse [Reference Rouse22] shows for quaternary forms that
$\det Q$
is a fundamental discriminant, Rouse [Reference Rouse22] shows for quaternary forms that
![]() $\langle \,f,f \rangle \asymp N$
if
$\langle \,f,f \rangle \asymp N$
if
![]() $\min(NQ^{-1}) \ll 1$
, where
$\min(NQ^{-1}) \ll 1$
, where
![]() $\min Q $
denotes the smallest integer represented by
$\min Q $
denotes the smallest integer represented by
![]() $q(x) = x^T Qx/2$
.
$q(x) = x^T Qx/2$
.
To state our results, we introduce further notation. For odd p, the form q(x) is equivalent over
![]() ${\mathbb Z}_p$
to
${\mathbb Z}_p$
to
and over
![]() ${\mathbb Z}_2$
to
${\mathbb Z}_2$
to
 \begin{align} \sum_{i=1}^{r_1} 2^{\tilde{\nu}_i} \left(x_{2i-1}^2 + x_{2i-1} x_{2i} + x_{2i}^2\right) + \sum_{i=r_1+1}^{r_2} 2^{\tilde{\nu}_i} x_{2i-1} x_{2i} + \sum_{i=2r_2+1}^m 2^{\nu_i(2)} u_i x_i^2,\end{align}
\begin{align} \sum_{i=1}^{r_1} 2^{\tilde{\nu}_i} \left(x_{2i-1}^2 + x_{2i-1} x_{2i} + x_{2i}^2\right) + \sum_{i=r_1+1}^{r_2} 2^{\tilde{\nu}_i} x_{2i-1} x_{2i} + \sum_{i=2r_2+1}^m 2^{\nu_i(2)} u_i x_i^2,\end{align}
where
![]() $u_i \in ({\mathbb Z}_2)^{\times}$
,
$u_i \in ({\mathbb Z}_2)^{\times}$
,
![]() $0 \le 2r_1 \le 2 r_2\le m$
and
$0 \le 2r_1 \le 2 r_2\le m$
and
![]() $\nu_i(2) \geq 1$
, cf. [Reference Jones19, theorem 33]. We set
$\nu_i(2) \geq 1$
, cf. [Reference Jones19, theorem 33]. We set
![]() $\nu_{2j}(2) = \nu_{2j-1}(2) \,{:\!=}\, \tilde{\nu}_j$
for
$\nu_{2j}(2) = \nu_{2j-1}(2) \,{:\!=}\, \tilde{\nu}_j$
for
![]() $j \leq r_2$
and define
$j \leq r_2$
and define
![]() $v_p(j) = \# \{1 \leq i \le m \mid \nu_i(p) \ge j\}$
. Moreover, for
$v_p(j) = \# \{1 \leq i \le m \mid \nu_i(p) \ge j\}$
. Moreover, for
![]() $s \geq 1$
, we set
$s \geq 1$
, we set
 \begin{align} F(Q,s) \,{:\!=}\, 2^{\textrm{min}(m -2 r_2,s)} \prod_{p \mid N} p^{\mu_p(s)} \quad \text{for} \quad \mu_p(s) = \sum_{j=1}^{v_p(N)} \min(v_p(j),s).\end{align}
\begin{align} F(Q,s) \,{:\!=}\, 2^{\textrm{min}(m -2 r_2,s)} \prod_{p \mid N} p^{\mu_p(s)} \quad \text{for} \quad \mu_p(s) = \sum_{j=1}^{v_p(N)} \min(v_p(j),s).\end{align}
Note that F(Q, s) is growing in s and
![]() $N/2 \leq F(Q,s) \leq F(Q,m) = \det Q$
. If most entries are coprime, then F(Q, s) is simply the determinant. For example, a diagonal form satisfies
$N/2 \leq F(Q,s) \leq F(Q,m) = \det Q$
. If most entries are coprime, then F(Q, s) is simply the determinant. For example, a diagonal form satisfies
![]() $F(Q,s) = \det Q$
if the common divisor of any
$F(Q,s) = \det Q$
if the common divisor of any
![]() $\lfloor s \rfloor +1$
diagonal terms is 1.
$\lfloor s \rfloor +1$
diagonal terms is 1.
Theorem 1. Let Q correspond to a primitive, integral, positive quadratic form of level N in m variables and
![]() $f(z)=\theta(Q,z) - \theta(\mathrm{gen}\ Q,z)$
. Then,
$f(z)=\theta(Q,z) - \theta(\mathrm{gen}\ Q,z)$
. Then,
 \begin{align*}\langle \,f,f \rangle \ll \begin{cases}\frac{N^{1+{\epsilon}}}{(\det Q)^{1/3}} & \text{if } m=3, \\ \\[-9pt] \frac{N^{2+{\epsilon}}}{F (Q,\,2)} + \frac{N^{1+{\epsilon}}}{(\det Q)^{1/4}} & \text{if } m=4, \\ \\[-9pt] \frac{N^{m/2+{\epsilon}}}{F (Q, \frac{m-1}{2}-\frac{1}{m})} & \text{if } m\geq 5.\end{cases}\end{align*}
\begin{align*}\langle \,f,f \rangle \ll \begin{cases}\frac{N^{1+{\epsilon}}}{(\det Q)^{1/3}} & \text{if } m=3, \\ \\[-9pt] \frac{N^{2+{\epsilon}}}{F (Q,\,2)} + \frac{N^{1+{\epsilon}}}{(\det Q)^{1/4}} & \text{if } m=4, \\ \\[-9pt] \frac{N^{m/2+{\epsilon}}}{F (Q, \frac{m-1}{2}-\frac{1}{m})} & \text{if } m\geq 5.\end{cases}\end{align*}
These bounds also hold for
![]() $\langle g,g \rangle$
and
$\langle g,g \rangle$
and
![]() $g(z)= \theta(Q,z)-\theta(Q',z)$
provided that Q
$g(z)= \theta(Q,z)-\theta(Q',z)$
provided that Q
![]() $^{\prime}$
lies in the same genus as Q.
$^{\prime}$
lies in the same genus as Q.
This is a significant improvement over previous results. For example, if
![]() $m\geq 4$
and
$m\geq 4$
and
![]() $\det Q \asymp N$
, we obtain
$\det Q \asymp N$
, we obtain
![]() $\langle \,f,f \rangle \ll N^{\frac{m}{2}-1}$
instead of
$\langle \,f,f \rangle \ll N^{\frac{m}{2}-1}$
instead of
![]() $\langle \,f,f \rangle \ll N^{m-2}$
in [Reference Sardari24]. This saving even increases if the determinant is larger than the level.
$\langle \,f,f \rangle \ll N^{m-2}$
in [Reference Sardari24]. This saving even increases if the determinant is larger than the level.
In applications, one often encounters special types of quadratic forms. A typical example are diagonal forms:
Theorem 2. Let Q, N, f be as in the previous theorem. In addition, we assume that Q is diagonal with entries
![]() $a_1 \le \cdots \le a_m$
and
$a_1 \le \cdots \le a_m$
and
![]() $m \geq 3$
. Then,
$m \geq 3$
. Then,
 \begin{align*} \langle \,f,f \rangle \ll \left(\frac{N^\frac{m}{2}}{F(Q, \frac{m}{2})} + \frac{ N }{\sqrt{a_m a_{m-1}}}\right) N^{\epsilon}. \end{align*}
\begin{align*} \langle \,f,f \rangle \ll \left(\frac{N^\frac{m}{2}}{F(Q, \frac{m}{2})} + \frac{ N }{\sqrt{a_m a_{m-1}}}\right) N^{\epsilon}. \end{align*}
Here,
![]() $F(Q,{m}/{2}) \asymp \det Q$
if
$F(Q,{m}/{2}) \asymp \det Q$
if
![]() $(a_{\pi(1)},\ldots,a_{\pi(j)}) \ll 1$
for every
$(a_{\pi(1)},\ldots,a_{\pi(j)}) \ll 1$
for every
![]() $\pi \in S_m$
and
$\pi \in S_m$
and
![]() $j \,{:\!=}\, \lfloor{m}/{2} \rfloor +1$
. We also provide a lower bound:
$j \,{:\!=}\, \lfloor{m}/{2} \rfloor +1$
. We also provide a lower bound:
Theorem 3. Let Q, n, f be defined as in Theorem 1 and
![]() $M = \min_{x \in {\mathbb Z}^m} x^T N Q^{-1}x/2$
. Then, it holds for
$M = \min_{x \in {\mathbb Z}^m} x^T N Q^{-1}x/2$
. Then, it holds for
![]() $m \geq 3$
that
$m \geq 3$
that
This shows that, without further assumptions, our analysis is sharp. Indeed, for
![]() $q(x) = x_1^2 + \cdots + x_{m-1}^2 + N x_m^2$
upper and lower bounds in Theorem 2 and 3 only differ by an
$q(x) = x_1^2 + \cdots + x_{m-1}^2 + N x_m^2$
upper and lower bounds in Theorem 2 and 3 only differ by an
![]() $N^{\epsilon}$
factor. For the minimum M of
$N^{\epsilon}$
factor. For the minimum M of
![]() $NQ^{-1}$
Hermite’s theorem states that
$NQ^{-1}$
Hermite’s theorem states that
![]() $M \ll N (\det Q)^{-\frac{1}{m}}$
, which yields that
$M \ll N (\det Q)^{-\frac{1}{m}}$
, which yields that
![]() $\langle \,f,f \rangle \gg N (\det Q)^{-\frac{1}{2}-\frac{1}{m}} + \mathcal{O}(N^{\epsilon})$
.
$\langle \,f,f \rangle \gg N (\det Q)^{-\frac{1}{2}-\frac{1}{m}} + \mathcal{O}(N^{\epsilon})$
.
One of the key ingredients for the proofs of Theorem 1 and 2 is Lemma 9 which states
 \begin{align*} \sum_{n \leq x} r(\tilde{Q},n)^2 \ll \left(1 + \frac{x^\frac{1}{2}}{\sqrt{a_1}} + \frac{x}{\sqrt{a_1 a_2}} + \cdots + \frac{x^{m-1}}{\sqrt{a_1 a_2} a_3 \cdots a_m} \right) x^{\epsilon}\end{align*}
\begin{align*} \sum_{n \leq x} r(\tilde{Q},n)^2 \ll \left(1 + \frac{x^\frac{1}{2}}{\sqrt{a_1}} + \frac{x}{\sqrt{a_1 a_2}} + \cdots + \frac{x^{m-1}}{\sqrt{a_1 a_2} a_3 \cdots a_m} \right) x^{\epsilon}\end{align*}
for a quadratic form
![]() $\tilde{Q}$
and any
$\tilde{Q}$
and any
![]() $x \in {\mathbb N}$
. Here,
$x \in {\mathbb N}$
. Here,
![]() $a_i$
are the successive minima of
$a_i$
are the successive minima of
![]() $\tilde{Q}$
, which are ordered by size and satisfy
$\tilde{Q}$
, which are ordered by size and satisfy
![]() $a_1 \cdots a_m = \det \tilde{Q}$
. The novelty here is to show that these
$a_1 \cdots a_m = \det \tilde{Q}$
. The novelty here is to show that these
![]() $a_i$
are bounded (up to a constant) by the level of
$a_i$
are bounded (up to a constant) by the level of
![]() $\tilde{Q}$
. This allows a much better treatment of the middle terms. For example, let
$\tilde{Q}$
. This allows a much better treatment of the middle terms. For example, let
![]() $x=N$
,
$x=N$
,
![]() $\tilde{Q} = NQ^{-1}$
and consider
$\tilde{Q} = NQ^{-1}$
and consider
 \begin{align*} \frac{N^{m-2}}{\sqrt{a_1 a_2} a_3 \cdots a_{m-1}} = \frac{N^{m-2} \sqrt{a_1} \sqrt{a_2} a_m }{\det NQ^{-1}} \ll \frac{N^{m-2} (\det N Q^{-1})^{\frac{1}{m}} N}{N^{m} (\det Q)^{-1}} = (\det Q)^{1- \frac{1}{m}}.\end{align*}
\begin{align*} \frac{N^{m-2}}{\sqrt{a_1 a_2} a_3 \cdots a_{m-1}} = \frac{N^{m-2} \sqrt{a_1} \sqrt{a_2} a_m }{\det NQ^{-1}} \ll \frac{N^{m-2} (\det N Q^{-1})^{\frac{1}{m}} N}{N^{m} (\det Q)^{-1}} = (\det Q)^{1- \frac{1}{m}}.\end{align*}
Previous works, such as [Reference Sardari24], simply estimated this term by
![]() $N^{m-2}$
. Together with an explicit transformation formual for the theta series, cf. Lemma 12, this gives the huge saving in Theorem 1 and 2.
$N^{m-2}$
. Together with an explicit transformation formual for the theta series, cf. Lemma 12, this gives the huge saving in Theorem 1 and 2.
The principal use of Theorem 1 and 2 is to improve the error
![]() $|r(Q,n) - r(\textrm{gen}\ Q,n)|$
. For the corresponding results and effective lower bounds for Tartakovski’s theorem with respect to Q, we refer the reader to Lemma 13 and 14.
$|r(Q,n) - r(\textrm{gen}\ Q,n)|$
. For the corresponding results and effective lower bounds for Tartakovski’s theorem with respect to Q, we refer the reader to Lemma 13 and 14.
1·3 Applications
By Gauss and Siegel it is known that every positive integer
![]() $n \not \equiv 0,4,7 \,(\textrm{mod}\ 8)$
can be expressed as a sum of three squares
$n \not \equiv 0,4,7 \,(\textrm{mod}\ 8)$
can be expressed as a sum of three squares
![]() $n=x_1^2 + x_2^2 + x_3^2$
in
$n=x_1^2 + x_2^2 + x_3^2$
in
![]() $n^{\frac{1}{2}+o(1)}$
ways. Therefore, one would expect that we can still represent n if we restrict
$n^{\frac{1}{2}+o(1)}$
ways. Therefore, one would expect that we can still represent n if we restrict
![]() $x_j$
to a plausible subset of the integers and there is no obvious local obstruction. A famous conjecture in this regard is that every
$x_j$
to a plausible subset of the integers and there is no obvious local obstruction. A famous conjecture in this regard is that every
can be represented as the sum of three squares of primes. Current technology is not sufficient to prove this; however, using a vector sieve, Blomer and Brüdern [Reference Blomer and Brüdern3] obtain similar findings for almost primes. The principal input for this sieve is a uniform bound for
![]() $ r(Q,n) - r(\textrm{gen}\ Q,n)$
, where
$ r(Q,n) - r(\textrm{gen}\ Q,n)$
, where
![]() $q(x)= x^T Q x/2 = l_1^2 x_1^2 + l_2^2 x_2^2 + l_3^2 x_3^2$
.
$q(x)= x^T Q x/2 = l_1^2 x_1^2 + l_2^2 x_2^2 + l_3^2 x_3^2$
.
By this approach, they show that every n satisfying (7) is represented by
where
![]() $P_r$
denotes all integers with at most r prime factors. Subsequently, Lü [Reference Lü20] and Cai [Reference Cai7] optimised the sieving process by including weights and Blomer [Reference Blomer2] improved his estimates for Fourier coefficients of the cuspidal part of the theta series. Taken together, this allows to choose
$P_r$
denotes all integers with at most r prime factors. Subsequently, Lü [Reference Lü20] and Cai [Reference Cai7] optimised the sieving process by including weights and Blomer [Reference Blomer2] improved his estimates for Fourier coefficients of the cuspidal part of the theta series. Taken together, this allows to choose
![]() $x_j \in P_{106}$
and
$x_j \in P_{106}$
and
![]() $x_1 x_2 x_3 \in P_{304}$
. By Theorem 1 and a small modification of Lü’s approach, we obtain:
$x_1 x_2 x_3 \in P_{304}$
. By Theorem 1 and a small modification of Lü’s approach, we obtain:
Corollary 4. Every sufficiently large n with
![]() $n \equiv 3 \,(\mathrm{mod}\ 24)$
and
$n \equiv 3 \,(\mathrm{mod}\ 24)$
and
![]() $5 \nmid n$
can be represented in the form
$5 \nmid n$
can be represented in the form
![]() $n=x_1^2 + x_2^2 + x_3^2$
for integers
$n=x_1^2 + x_2^2 + x_3^2$
for integers
![]() $x_1,x_2,x_3$
with
$x_1,x_2,x_3$
with
![]() $x_1 x_2 x_3 \in P_{72}$
.
$x_1 x_2 x_3 \in P_{72}$
.
The dual problem is to represent an integer by squares of smooth numbers. For three variables, this is a hard task and only a small saving is possible. An application of Theorem 2 yields:
Corollary 5. For sufficiently large
![]() $n \not\equiv 0,4,7\,(\mathrm{mod}\ 8)$
, there is a solution of
$n \not\equiv 0,4,7\,(\mathrm{mod}\ 8)$
, there is a solution of
![]() ${n= x_1^2 + \cdots + x_m^2}$
with
${n= x_1^2 + \cdots + x_m^2}$
with
![]() $x_1,\ldots,x_m \in {\mathbb Z}$
such that every prime divisor
$x_1,\ldots,x_m \in {\mathbb Z}$
such that every prime divisor
![]() $p \mid x_1\cdots x_m$
satisfies
$p \mid x_1\cdots x_m$
satisfies
 \begin{align*} &p \leq n^{\frac{\eta}{2}+{\epsilon}}, \eta = \frac{57}{58} \quad \ \ \text{if } m=3 \text { and } n \equiv 0,4,7 \, (\mathrm{mod}\ 8), \\[3pt] &p \leq n^{\frac{\theta}{2}+{\epsilon}}, \theta = \frac{285}{464} \quad \text{if } m=4.\end{align*}
\begin{align*} &p \leq n^{\frac{\eta}{2}+{\epsilon}}, \eta = \frac{57}{58} \quad \ \ \text{if } m=3 \text { and } n \equiv 0,4,7 \, (\mathrm{mod}\ 8), \\[3pt] &p \leq n^{\frac{\theta}{2}+{\epsilon}}, \theta = \frac{285}{464} \quad \text{if } m=4.\end{align*}
These are slight improvements of [Reference Blomer, Brüdern and Dietmann4, Theorems 2 and 3], where
![]() $\eta = {73}/{74}$
and
$\eta = {73}/{74}$
and
![]() $\theta\,{=}\,365/592$
.
$\theta\,{=}\,365/592$
.
Notation and conventions. We use the usual
![]() $\epsilon$
-convention and all implied constants may depend on
$\epsilon$
-convention and all implied constants may depend on
![]() $\epsilon$
. Furthermore, we assume that all quadratic forms have finite rank. By
$\epsilon$
. Furthermore, we assume that all quadratic forms have finite rank. By
![]() $[.,.], (.,.)$
we refer to the least common multiple respectively the greatest common divisor of two integers. If
$[.,.], (.,.)$
we refer to the least common multiple respectively the greatest common divisor of two integers. If
![]() $p^r \mid N$
, but
$p^r \mid N$
, but
![]() $p^{r+1} \nmid N$
, we write
$p^{r+1} \nmid N$
, we write
![]() $p^{r} \mid\!\mid N$
.
$p^{r} \mid\!\mid N$
.
2. Siegel’s theory and local densities
For a holomorphic function f on the upper half plane and
![]() $\gamma \in \Gamma_0(N)$
we write
$\gamma \in \Gamma_0(N)$
we write
 \begin{align*}f|[\gamma]_{\frac{m}{2}}(z) \,{:\!=}\, \begin{cases}(cz+d)^{-\frac{m}{2}} f(\gamma z) & \text{if } m \text{ is even} \\ \\[-7pt] \left({\epsilon}_d \big(\frac{c}{d}\big)\right)^{-m} (cz+d)^{-\frac{m}{2}} f(\gamma z) & \text{if } m \text{ is odd and } 4 \mid N ,\end{cases}\end{align*}
\begin{align*}f|[\gamma]_{\frac{m}{2}}(z) \,{:\!=}\, \begin{cases}(cz+d)^{-\frac{m}{2}} f(\gamma z) & \text{if } m \text{ is even} \\ \\[-7pt] \left({\epsilon}_d \big(\frac{c}{d}\big)\right)^{-m} (cz+d)^{-\frac{m}{2}} f(\gamma z) & \text{if } m \text{ is odd and } 4 \mid N ,\end{cases}\end{align*}
where
![]() $\big({c}/{d}\big)$
is the extended Kronecker symbol and
$\big({c}/{d}\big)$
is the extended Kronecker symbol and
![]() ${\epsilon}_d = \left({-1}/{d}\right)^\frac{1}{2}$
. Moreover, we denote by
${\epsilon}_d = \left({-1}/{d}\right)^\frac{1}{2}$
. Moreover, we denote by
![]() $S_{m/2}(N,\chi)$
the space of cusp forms of weight
$S_{m/2}(N,\chi)$
the space of cusp forms of weight
![]() $\frac{m}{2} $
for
$\frac{m}{2} $
for
![]() $\Gamma_0(N)$
and character
$\Gamma_0(N)$
and character
![]() $\chi$
.
$\chi$
.
Two positive, quadratic forms Q, Q
![]() $^{\prime}$
belong to the same class if
$^{\prime}$
belong to the same class if
![]() $Q' = U^T Q U$
for
$Q' = U^T Q U$
for
![]() $U \in \textrm{GL}_m({\mathbb Z})$
. Furthermore, they are in the same genus if they are equivalent over
$U \in \textrm{GL}_m({\mathbb Z})$
. Furthermore, they are in the same genus if they are equivalent over
![]() ${\mathbb Z}_p$
for all p, so in particular over
${\mathbb Z}_p$
for all p, so in particular over
![]() ${\mathbb Q}$
. There are only finitely many classes in the genus and the set of automorphs
${\mathbb Q}$
. There are only finitely many classes in the genus and the set of automorphs
![]() $o(Q) \,{:\!=}\,\{ U \in \textrm{GL}_2({\mathbb Z}) \mid U^T Q U = Q\}$
is finite. We put
$o(Q) \,{:\!=}\,\{ U \in \textrm{GL}_2({\mathbb Z}) \mid U^T Q U = Q\}$
is finite. We put
 \begin{align*}\theta(\textrm{gen}\ Q,z)= \left(\sum_{R \in \textrm{gen}\ Q} \frac{1}{\#o(R)} \right)^{-1} \sum_{R \in \textrm{gen}\ Q} \frac{\theta(R,Z)}{\#o(R)} = \sum_{n} r(\textrm{gen}\ Q,n) e(nz).\end{align*}
\begin{align*}\theta(\textrm{gen}\ Q,z)= \left(\sum_{R \in \textrm{gen}\ Q} \frac{1}{\#o(R)} \right)^{-1} \sum_{R \in \textrm{gen}\ Q} \frac{\theta(R,Z)}{\#o(R)} = \sum_{n} r(\textrm{gen}\ Q,n) e(nz).\end{align*}
Throughout this work, we assume that
![]() $q(x) = x^T Qx/2$
is primitive. This implies that
$q(x) = x^T Qx/2$
is primitive. This implies that
![]() $NQ^{-1}$
has level N and that
$NQ^{-1}$
has level N and that
![]() $N/2 \mid \det Q \mid 2 N^{m-1}.$
$N/2 \mid \det Q \mid 2 N^{m-1}.$
Recall that
![]() $\theta(Q,z) - \theta(\textrm{gen}\ Q,z) \in S_{m/2}(N,\chi)$
. The space
$\theta(Q,z) - \theta(\textrm{gen}\ Q,z) \in S_{m/2}(N,\chi)$
. The space
![]() $S_{3/2}(N,\chi)$
contains a subspace U generated by theta functions of the form
$S_{3/2}(N,\chi)$
contains a subspace U generated by theta functions of the form
![]() $\sum \psi(n) n e(tn^2z)$
for some real character
$\sum \psi(n) n e(tn^2z)$
for some real character
![]() $\psi$
and
$\psi$
and
![]() $t \mid 4N$
. Their non-vanishing Fourier coefficients are of size
$t \mid 4N$
. Their non-vanishing Fourier coefficients are of size
![]() $\asymp n^\frac{1}{2}$
which is the order of magnitude of
$\asymp n^\frac{1}{2}$
which is the order of magnitude of
![]() $r(\textrm{gen}\ Q,z)$
, cf. (1). Hence, for
$r(\textrm{gen}\ Q,z)$
, cf. (1). Hence, for
![]() $m=3$
the main term needs to be modified.
$m=3$
the main term needs to be modified.
Two quadratic forms
![]() $q_1,q_2$
with matrices
$q_1,q_2$
with matrices
![]() $Q_1 = S^T Q_2 S$
and
$Q_1 = S^T Q_2 S$
and
![]() $S \in \textrm{GL}_m({\mathbb Z})$
in the same genus belong to the same spinor genus if
$S \in \textrm{GL}_m({\mathbb Z})$
in the same genus belong to the same spinor genus if
![]() $S \in O_{Q}(A_2) \bigcap_{p} O'_{Q_p}(A_2)GL_{m}({\mathbb Z}_p)$
, where
$S \in O_{Q}(A_2) \bigcap_{p} O'_{Q_p}(A_2)GL_{m}({\mathbb Z}_p)$
, where
![]() $O'_{Q_p}(A)$
is the subgroup of p-adic automorphs
$O'_{Q_p}(A)$
is the subgroup of p-adic automorphs
![]() $O_{Q_p}(A)$
of determinant and spinor norm 1, cf. [Reference O’Meara21, section 55]. We set
$O_{Q_p}(A)$
of determinant and spinor norm 1, cf. [Reference O’Meara21, section 55]. We set
 \begin{align*}\theta(\textrm{spn}\ Q,z)= \left(\sum_{R \in \textrm{spn}\ Q} \frac{1}{\#o(R)} \right)^{-1} \sum_{R \in \textrm{spn}\ Q} \frac{\theta(R,Z)}{\#o(R)}.\end{align*}
\begin{align*}\theta(\textrm{spn}\ Q,z)= \left(\sum_{R \in \textrm{spn}\ Q} \frac{1}{\#o(R)} \right)^{-1} \sum_{R \in \textrm{spn}\ Q} \frac{\theta(R,Z)}{\#o(R)}.\end{align*}
Then,
![]() $\theta(Q,z) - \theta(\textrm{spn}\ Q,z) \in U^{\bot} \subseteq S_{3/2}(N,\chi)$
. For
$\theta(Q,z) - \theta(\textrm{spn}\ Q,z) \in U^{\bot} \subseteq S_{3/2}(N,\chi)$
. For
![]() $g(z) = \sum_n b(n) e(nz) \in U^\bot $
, we have by [Reference Waibel30, theorem 1] for
$g(z) = \sum_n b(n) e(nz) \in U^\bot $
, we have by [Reference Waibel30, theorem 1] for
![]() $n=tv^2w^2$
with squarefree t and
$n=tv^2w^2$
with squarefree t and
![]() $(w,N)=1$
that
$(w,N)=1$
that
 \begin{align} a(n) \ll {g} n^{\frac{1}{4}} \left( {1 + \frac{n^{\frac{3} {14}}}{N^{\frac 1 7}} + \frac{n^{\frac{3} {16}}}{N^{\frac{1} {16}}}+ \frac{\sqrt{v (n,N)}}{\sqrt{N}}} \right) (nN)^{{\epsilon}}.\end{align}
\begin{align} a(n) \ll {g} n^{\frac{1}{4}} \left( {1 + \frac{n^{\frac{3} {14}}}{N^{\frac 1 7}} + \frac{n^{\frac{3} {16}}}{N^{\frac{1} {16}}}+ \frac{\sqrt{v (n,N)}}{\sqrt{N}}} \right) (nN)^{{\epsilon}}.\end{align}
This saving in n is sufficient to obtain an asymptotic formula for r(Q, n), since by a local argument of Blomer, cf. [Reference Blomer2, (1·7)], we can assume that (n, N) is small.
In principle, the Fourier coefficients
![]() $ r (\textrm{spn}\ Q,n)$
of
$ r (\textrm{spn}\ Q,n)$
of
![]() $\theta(\textrm{spn}\ Q,z)$
can be computed locally in a similar fashion as
$\theta(\textrm{spn}\ Q,z)$
can be computed locally in a similar fashion as
![]() $r(\textrm{gen}\ Q,n)$
. However, this process is complicated and tedious. Luckily, in many situations
$r(\textrm{gen}\ Q,n)$
. However, this process is complicated and tedious. Luckily, in many situations
![]() $r (\textrm{spn}\ Q,n)$
and r(Q, n) coincide. For example, this holds if
$r (\textrm{spn}\ Q,n)$
and r(Q, n) coincide. For example, this holds if
 \begin{align} \begin{split}\textrm{(i)}\ &n \notin \{tm^2 \mid 4t \equiv 0\, (\textrm{mod}\ N), m \in {\mathbb N}\} \text{ or} \\ \\[-10pt] \textrm{(ii)}\ &q \simeq u_1 p^{\nu_1} x_1^2 + u_2 p^{\nu_2} x_2^2 + u_3 p^{\nu_3} x_2^2 \text{ over } {\mathbb Z}_p, \text{at least two } \nu_i \text { are equal for} \\[-3pt] &\text{odd } p \text{ and all three } \nu_i \text{ are equal for } p=2.\end{split}\end{align}
\begin{align} \begin{split}\textrm{(i)}\ &n \notin \{tm^2 \mid 4t \equiv 0\, (\textrm{mod}\ N), m \in {\mathbb N}\} \text{ or} \\ \\[-10pt] \textrm{(ii)}\ &q \simeq u_1 p^{\nu_1} x_1^2 + u_2 p^{\nu_2} x_2^2 + u_3 p^{\nu_3} x_2^2 \text{ over } {\mathbb Z}_p, \text{at least two } \nu_i \text { are equal for} \\[-3pt] &\text{odd } p \text{ and all three } \nu_i \text{ are equal for } p=2.\end{split}\end{align}
To obtain upper and lower bounds for
![]() $r(\textrm{gen}\ Q,n)$
, we need to evaluate the p-adic densities given in (2). If
$r(\textrm{gen}\ Q,n)$
, we need to evaluate the p-adic densities given in (2). If
![]() $p \nmid 2nN$
, an easy computation shows that
$p \nmid 2nN$
, an easy computation shows that
 \begin{align} \beta_p(n,Q) = \begin{cases}1- p^{-\frac{m}{2}}\left(\frac{(\!-1)^\frac{m}{2} \det Q }{p^\frac{m}{2}}\right) & \text{if } m \text{ even}, \\ \\[-9pt] 1 + p^{\frac{1-m}{2}} \left(\frac{(\!-1)^\frac{m-1}{2} n \det Q }{p^\frac{m}{2}}\right) & \text{if } m \text{ odd},\end{cases}\end{align}
\begin{align} \beta_p(n,Q) = \begin{cases}1- p^{-\frac{m}{2}}\left(\frac{(\!-1)^\frac{m}{2} \det Q }{p^\frac{m}{2}}\right) & \text{if } m \text{ even}, \\ \\[-9pt] 1 + p^{\frac{1-m}{2}} \left(\frac{(\!-1)^\frac{m-1}{2} n \det Q }{p^\frac{m}{2}}\right) & \text{if } m \text{ odd},\end{cases}\end{align}
cf. [Reference Siegel27, Hilfssatz 12]. For
![]() $p \nmid 2N$
, we have by [Reference Siegel27, Hilfssatz 16] that
$p \nmid 2N$
, we have by [Reference Siegel27, Hilfssatz 16] that
where
![]() $r= {m}/{2}$
for even m and
$r= {m}/{2}$
for even m and
![]() $r= {1-m}/{2}$
for odd m. For the remaining p-adic densities, we apply a formula of Yang [Reference Yang32]. For odd p and
$r= {1-m}/{2}$
for odd m. For the remaining p-adic densities, we apply a formula of Yang [Reference Yang32]. For odd p and
![]() $\nu_i, u_i$
defined as in (4), we set
$\nu_i, u_i$
defined as in (4), we set
and
 \begin{align} d(l) = l + \frac{1}{2}\sum_{\nu_i<l} (\nu_i-l), \quad v(l) = \left(\frac{-1}{p}\right)^{\lfloor \frac{\# V(l)}{2} \rfloor}\prod_{i \in V(l)} \left(\frac{u_i}{p}\right).\end{align}
\begin{align} d(l) = l + \frac{1}{2}\sum_{\nu_i<l} (\nu_i-l), \quad v(l) = \left(\frac{-1}{p}\right)^{\lfloor \frac{\# V(l)}{2} \rfloor}\prod_{i \in V(l)} \left(\frac{u_i}{p}\right).\end{align}
Lemma 6. [Reference Yang32, theorem 3·1] For odd p and
![]() $n= p^a t$
with
$n= p^a t$
with
![]() $(t,p)=1$
we have that
$(t,p)=1$
we have that
 \begin{align*} \beta_p(Q,n) = 1 + \left(1+p^{-1}\right) \sum_{\substack{0 < l \leq a \\ \#V(l)\, \text{even}}} v(l) p^{d(l)} + v(a+1) p^{d(a+1)} f(n) \end{align*}
\begin{align*} \beta_p(Q,n) = 1 + \left(1+p^{-1}\right) \sum_{\substack{0 < l \leq a \\ \#V(l)\, \text{even}}} v(l) p^{d(l)} + v(a+1) p^{d(a+1)} f(n) \end{align*}
where
 \begin{align*} f(n) = \begin{cases} - \frac{1}{p} & \text{if } \#V(a+1) \text{ is even,} \\ \\[-8pt] \left(\frac{t}{p}\right)\frac{1}{\sqrt{p}} & \text{if } \#V(a+1) \text{ is odd}. \end{cases} \end{align*}
\begin{align*} f(n) = \begin{cases} - \frac{1}{p} & \text{if } \#V(a+1) \text{ is even,} \\ \\[-8pt] \left(\frac{t}{p}\right)\frac{1}{\sqrt{p}} & \text{if } \#V(a+1) \text{ is odd}. \end{cases} \end{align*}
To compute the densities for odd
![]() $p \mid N, p\nmid n$
, we make a case distinction according to
$p \mid N, p\nmid n$
, we make a case distinction according to
![]() $V(1) = \#\{i \mid \nu_i =0 \}$
. If
$V(1) = \#\{i \mid \nu_i =0 \}$
. If
![]() $V(2) \geq 2$
it follows by the theorem above that
$V(2) \geq 2$
it follows by the theorem above that
For
![]() $V(1) =1$
, we obtain
$V(1) =1$
, we obtain
![]() $\beta_p(Q,n) = 1 + \Big( {n}/{p} \Big) \prod_{i \in V(1)} \Big({u_i}/{p} \Big)$
.
$\beta_p(Q,n) = 1 + \Big( {n}/{p} \Big) \prod_{i \in V(1)} \Big({u_i}/{p} \Big)$
.
For the computation of the 2-adic densities Yang provides a slightly more complex formula [Reference Yang32, theorem 4·1]. This gives the following upper bound:
Corollary 7. It holds that
Proof. By (10), (11) and (13) we already know that
Let
![]() $(n,N) = p^b$
. Then,
$(n,N) = p^b$
. Then,
![]() $d(l) \leq {b}/{2}$
for all l. Hence, Lemma 6 gives for odd p that
$d(l) \leq {b}/{2}$
for all l. Hence, Lemma 6 gives for odd p that
![]() $\beta_p(Q,n) \ll p^{\frac{b}{2}}$
as
$\beta_p(Q,n) \ll p^{\frac{b}{2}}$
as
![]() $|{v(l)}|=1$
. For
$|{v(l)}|=1$
. For
![]() $p=2$
we apply [Reference Yang32, theorem 4·1]. The term d(k), defined in [Reference Yang32, (4·3)], satisfies
$p=2$
we apply [Reference Yang32, theorem 4·1]. The term d(k), defined in [Reference Yang32, (4·3)], satisfies
![]() $d(k) \leq 2^{\frac{b+1}{2}}$
which implies that [Reference Yang32, (4·4)] is bounded by
$d(k) \leq 2^{\frac{b+1}{2}}$
which implies that [Reference Yang32, (4·4)] is bounded by
![]() $\ll 2^{\frac{b}{2}}$
and hence, also
$\ll 2^{\frac{b}{2}}$
and hence, also
![]() $\beta_2(n,Q)$
.
$\beta_2(n,Q)$
.
As a consequence, we obtain by (1) that
 \begin{align} r(\textrm{gen}\ Q,n) \ll \frac{n^{\frac{m}{2}-1}(n,N)^{\frac{1}{2}}}{\sqrt{\det Q}} (nN)^{\epsilon}.\end{align}
\begin{align} r(\textrm{gen}\ Q,n) \ll \frac{n^{\frac{m}{2}-1}(n,N)^{\frac{1}{2}}}{\sqrt{\det Q}} (nN)^{\epsilon}.\end{align}
To obtain lower bounds for
![]() $\beta_p(Q,n)$
we follow the approach of Hanke [Reference Hanke15]. For
$\beta_p(Q,n)$
we follow the approach of Hanke [Reference Hanke15]. For
![]() $q \simeq u_1 p^{\nu_1} x_1^2 + \cdots + u_m p^{\nu_m} x_m^2 $
in the form (4) and a primitive solution
$q \simeq u_1 p^{\nu_1} x_1^2 + \cdots + u_m p^{\nu_m} x_m^2 $
in the form (4) and a primitive solution
![]() $x \in ({\mathbb Z}_p)^m$
of
$x \in ({\mathbb Z}_p)^m$
of
![]() $q(x) = n$
, we set
$q(x) = n$
, we set
We say that x is of good type if
![]() $\nu(x)=0$
, of bad type I if
$\nu(x)=0$
, of bad type I if
![]() $\nu(x)=1$
and of bad type II if
$\nu(x)=1$
and of bad type II if
![]() $\nu(x) \ge 2$
. If there is a solution of good type, we count solutions modulo p and apply Hensel’s lemma to compute
$\nu(x) \ge 2$
. If there is a solution of good type, we count solutions modulo p and apply Hensel’s lemma to compute
![]() $\beta_p(q,n)$
. As a result, we obtain
$\beta_p(q,n)$
. As a result, we obtain
![]() $\beta_p(q,n) \geq 1- {1}/{p}$
and
$\beta_p(q,n) \geq 1- {1}/{p}$
and
![]() $\beta_2(q,n) \geq {1}/{4}$
.
$\beta_2(q,n) \geq {1}/{4}$
.
In all other cases, we apply reduction maps. Therefore, let
![]() $q \equiv q_0 + p q_1 + p^2 q_2$
, where
$q \equiv q_0 + p q_1 + p^2 q_2$
, where
![]() $q_0$
consist of all diagonal terms with
$q_0$
consist of all diagonal terms with
![]() $\nu_i=0$
and
$\nu_i=0$
and
![]() $pq_1$
of those with
$pq_1$
of those with
![]() $\nu_i=1$
. If there are no good solutions, but at least one of bad type I, we reduce modulo p which gives
$\nu_i=1$
. If there are no good solutions, but at least one of bad type I, we reduce modulo p which gives
![]() $\beta_p(q,n) \geq p^{1-\dim q_0} \beta_p(q',{n}/{p})$
for
$\beta_p(q,n) \geq p^{1-\dim q_0} \beta_p(q',{n}/{p})$
for
![]() $q' = p q_0 + q_1 + p q_2$
. If there are only bad type II solutions, we reduce modulo
$q' = p q_0 + q_1 + p q_2$
. If there are only bad type II solutions, we reduce modulo
![]() $p^2$
which gives
$p^2$
which gives
![]() $\beta_p(q,n) \geq p^{2-\dim q_0-\dim q_1} \beta_p(q'',{n}/{p^2})$
for
$\beta_p(q,n) \geq p^{2-\dim q_0-\dim q_1} \beta_p(q'',{n}/{p^2})$
for
![]() $q'' = q_0 + p q_1 + q_2$
. As a consequence, we obtain:
$q'' = q_0 + p q_1 + q_2$
. As a consequence, we obtain:
Lemma 8. Assume there is a primitive solution
![]() $q(x) = n$
over
$q(x) = n$
over
![]() ${\mathbb Z}_p$
with
${\mathbb Z}_p$
with
![]() $\nu \,{:\!=}\, \nu(x)$
as above and
$\nu \,{:\!=}\, \nu(x)$
as above and
![]() $m \geq 4$
. Then,
$m \geq 4$
. Then,
Furthermore, we have for
![]() $m=4$
that
$m=4$
that
 \begin{align*}r_p(q,n) \geq \frac{1- \frac{1}{p}}{\sqrt{(p^{\nu},n)}} \text{ for } p \equiv 3\,( \mathrm{mod}\ 4) \text{ and } r_2(q,n) \geq \frac{1}{32 \cdot \sqrt{(2^{\nu},n)}}\end{align*}
\begin{align*}r_p(q,n) \geq \frac{1- \frac{1}{p}}{\sqrt{(p^{\nu},n)}} \text{ for } p \equiv 3\,( \mathrm{mod}\ 4) \text{ and } r_2(q,n) \geq \frac{1}{32 \cdot \sqrt{(2^{\nu},n)}}\end{align*}
and for
![]() $m \geq 5$
that
$m \geq 5$
that
Remark. It seems counterintuitive that the bounds for
![]() $m=4$
are stronger. One reason is the assumption that n is primitively locally represented which eliminates the worst case scenario for the lower bound, i.e. that
$m=4$
are stronger. One reason is the assumption that n is primitively locally represented which eliminates the worst case scenario for the lower bound, i.e. that
![]() $q \sim x_1^2 + x_2^2 + p x_3^2 + p x_4^2$
and
$q \sim x_1^2 + x_2^2 + p x_3^2 + p x_4^2$
and
![]() $p \equiv 3 \,(\textrm{mod}\ 4)$
.
$p \equiv 3 \,(\textrm{mod}\ 4)$
.
Proof. The case
![]() $m=4$
is essentially proven in [Reference Rouse23, lemma 2]. If
$m=4$
is essentially proven in [Reference Rouse23, lemma 2]. If
![]() $p \equiv 1\, (\textrm{mod}\ 4)$
and
$p \equiv 1\, (\textrm{mod}\ 4)$
and
![]() $\dim q_0 \geq 2$
, there is always a good solution. Moreover, a bad type solution cannot exist for
$\dim q_0 \geq 2$
, there is always a good solution. Moreover, a bad type solution cannot exist for
![]() $q \simeq u_1 x_1^2 + u_2 x_2^2 + u_3 p x_3^2 + u_4 p x_4$
if
$q \simeq u_1 x_1^2 + u_2 x_2^2 + u_3 p x_3^2 + u_4 p x_4$
if
![]() $p \equiv 3 \,(\textrm{mod}\ 4)$
. Indeed, all solutions of
$p \equiv 3 \,(\textrm{mod}\ 4)$
. Indeed, all solutions of
![]() $x_1^2 + x_2^2 + p x_3^2 + p x_4^2 \equiv 0 \,(\textrm{mod}\ p^2)$
satisfy
$x_1^2 + x_2^2 + p x_3^2 + p x_4^2 \equiv 0 \,(\textrm{mod}\ p^2)$
satisfy
![]() $x \equiv 0 \,(\textrm{mod}\ p)$
for
$x \equiv 0 \,(\textrm{mod}\ p)$
for
![]() $p \equiv 3 \,(\textrm{mod}\ 4)$
. The cases
$p \equiv 3 \,(\textrm{mod}\ 4)$
. The cases
![]() $m \geq 5$
work analogously to
$m \geq 5$
work analogously to
![]() $m=4$
.
$m=4$
.
Since
![]() $\nu \leq v_p(N)$
, it follows for
$\nu \leq v_p(N)$
, it follows for
![]() $m=4$
that
$m=4$
that
![]() $\prod_p \beta_p(q,n) \gg (n,N)^{-\frac{1}{2}} (nN)^{-{\epsilon}}$
if n is primitively represented. A form in 5 variables is isotropic over
$\prod_p \beta_p(q,n) \gg (n,N)^{-\frac{1}{2}} (nN)^{-{\epsilon}}$
if n is primitively represented. A form in 5 variables is isotropic over
![]() ${\mathbb Z}_p$
and hence if we sort
${\mathbb Z}_p$
and hence if we sort
![]() $\nu_i$
by value, there is always a primitive solution x such that
$\nu_i$
by value, there is always a primitive solution x such that
![]() $\nu(x) \le \nu_5$
. Hence, we obtain for
$\nu(x) \le \nu_5$
. Hence, we obtain for
![]() $m \geq 5$
that
$m \geq 5$
that
 \begin{align*}\prod_p \beta_p(q,n) \gg \prod_{p \mid N} \left( p^{\frac{v_p(\det Q)}{m-4}}, p^{v_p(N)},n\right) ^{-1}(nN)^{-{\epsilon}}.\end{align*}
\begin{align*}\prod_p \beta_p(q,n) \gg \prod_{p \mid N} \left( p^{\frac{v_p(\det Q)}{m-4}}, p^{v_p(N)},n\right) ^{-1}(nN)^{-{\epsilon}}.\end{align*}
For a given form, it is often possible to find a primitive solution with
![]() $\nu=0$
for all
$\nu=0$
for all
![]() $p \mid (n,N)$
which yields
$p \mid (n,N)$
which yields
![]() $\prod_p \beta_p(q,n) \gg (nN)^{-{\epsilon}}$
.
$\prod_p \beta_p(q,n) \gg (nN)^{-{\epsilon}}$
.
3. A uniform bound for the inner product
The aim of this section is to prove Theorem 1, 2 and 3. Recall that the Siegel domain
![]() $\mathcal{S}(\delta,\eta)$
consists of all positive matrices M that allow for a decomposition into
$\mathcal{S}(\delta,\eta)$
consists of all positive matrices M that allow for a decomposition into
where V is an upper triangular matrix with ones on the diagonal and all other entries
![]() $|{v_{i,j}}| \leq \eta$
and D is a diagonal matrix with entries
$|{v_{i,j}}| \leq \eta$
and D is a diagonal matrix with entries
![]() $a_1, \ldots, a_{m} $
that satisfy
$a_1, \ldots, a_{m} $
that satisfy
![]() $0 < a_i \leq \delta a_{i+1}$
.
$0 < a_i \leq \delta a_{i+1}$
.
Let Q denote a positive, integral matrix with even diagonal entries. By [Reference Cassels8, p. 259], the class of Q contains an element
![]() $Q' \in \mathcal{S}({4}/{3},{1}/{2})$
. We decompose
$Q' \in \mathcal{S}({4}/{3},{1}/{2})$
. We decompose
![]() $Q'=V^T DV$
as above and call
$Q'=V^T DV$
as above and call
![]() $a_1,\ldots,a_m$
the associated diagonal entries of Q. Since
$a_1,\ldots,a_m$
the associated diagonal entries of Q. Since
![]() $a_1$
equals the upper left entry of Q
$a_1$
equals the upper left entry of Q
![]() $^{\prime}$
it is integral and thus,
$^{\prime}$
it is integral and thus,
![]() $a_1 \geq 1$
. This construction of
$a_1 \geq 1$
. This construction of
![]() $a_1,\ldots,a_m$
with respect to Q is not unique. If we assume that Q
$a_1,\ldots,a_m$
with respect to Q is not unique. If we assume that Q
![]() $^{\prime}$
is Hermite-reduced, then
$^{\prime}$
is Hermite-reduced, then
![]() $a_i$
is of the same size as the i-th successive minimum of Q, cf. [Reference Cassels8, section 12, theorem 3·1].
$a_i$
is of the same size as the i-th successive minimum of Q, cf. [Reference Cassels8, section 12, theorem 3·1].
Lemma 9. Let Q correspond to a positive, integral quadratic form of level N with associated diagonal entries
![]() $a_1,\ldots,a_m$
. Then,
$a_1,\ldots,a_m$
. Then,
Furthermore, it holds that
 \begin{align} \sum_{x \leq l} r(Q,x)^2 \ll \left(1 + \frac{l^\frac{1}{2}}{\sqrt{a_1}} + \frac{l}{\sqrt{a_1 a_2}} + \cdots + \frac{l^{m-1}}{\sqrt{a_1 a_2} a_3 \cdots a_m} \right) l^{\epsilon}.\end{align}
\begin{align} \sum_{x \leq l} r(Q,x)^2 \ll \left(1 + \frac{l^\frac{1}{2}}{\sqrt{a_1}} + \frac{l}{\sqrt{a_1 a_2}} + \cdots + \frac{l^{m-1}}{\sqrt{a_1 a_2} a_3 \cdots a_m} \right) l^{\epsilon}.\end{align}
More precisely, for
![]() $2 \le j \le 2m-2$
the j-th term is given by
$2 \le j \le 2m-2$
the j-th term is given by
![]() $\frac{l^{j/2}}{ A_j}$
where
$\frac{l^{j/2}}{ A_j}$
where
 \begin{align*}A_j = \prod_{i=1}^{\lfloor \frac{j+3}{2} \rfloor} \sqrt{a_i} \prod_{k=3}^{\lfloor \frac{j+2}{2} \rfloor} \sqrt{a_k} = \det Q \left(\sqrt{a_1 a_2} \prod_{i= \lfloor \frac{j+5}{2} \rfloor}^{m} \sqrt{a_i} \prod_{k=\lfloor \frac{j+4}{2} \rfloor}^{m} \sqrt{a_k}\right)^{-1}.\end{align*}
\begin{align*}A_j = \prod_{i=1}^{\lfloor \frac{j+3}{2} \rfloor} \sqrt{a_i} \prod_{k=3}^{\lfloor \frac{j+2}{2} \rfloor} \sqrt{a_k} = \det Q \left(\sqrt{a_1 a_2} \prod_{i= \lfloor \frac{j+5}{2} \rfloor}^{m} \sqrt{a_i} \prod_{k=\lfloor \frac{j+4}{2} \rfloor}^{m} \sqrt{a_k}\right)^{-1}.\end{align*}
Moreover, we have
 \begin{align*} \sum_{x \leq l} r(NQ^{-1},x)^2 \ll \left(1 + \frac{ l^{\frac{1}{2}}\sqrt{a_{m}}}{\sqrt{N}} + \sum_{j=2}^{2m-2} \frac{l^\frac{j}{2} \tilde{A}_j }{N^\frac{j}{2} } \right) l^{\epsilon}, \end{align*}
\begin{align*} \sum_{x \leq l} r(NQ^{-1},x)^2 \ll \left(1 + \frac{ l^{\frac{1}{2}}\sqrt{a_{m}}}{\sqrt{N}} + \sum_{j=2}^{2m-2} \frac{l^\frac{j}{2} \tilde{A}_j }{N^\frac{j}{2} } \right) l^{\epsilon}, \end{align*}
where
 \begin{align*}\tilde{A}_j \! = \! \! \prod_{i=m-\lfloor \frac{j+1}{2} \rfloor}^{m} \! \sqrt{a_i} \prod_{k=m-\lfloor \frac{j}{2} \rfloor}^{m-2} \sqrt{a_k}.\end{align*}
\begin{align*}\tilde{A}_j \! = \! \! \prod_{i=m-\lfloor \frac{j+1}{2} \rfloor}^{m} \! \sqrt{a_i} \prod_{k=m-\lfloor \frac{j}{2} \rfloor}^{m-2} \sqrt{a_k}.\end{align*}
Proof. Since
![]() $r(Q,n) = r(U^T Q U, n)$
for any
$r(Q,n) = r(U^T Q U, n)$
for any
![]() $U \in \textrm{GL}_{m}({\mathbb Z})$
, we may assume that
$U \in \textrm{GL}_{m}({\mathbb Z})$
, we may assume that
![]() $Q \in \mathcal{S}({4}/{3},{1}/{2})$
. If we decompose
$Q \in \mathcal{S}({4}/{3},{1}/{2})$
. If we decompose
![]() $Q=V^T D V$
with V and D as above, we obtain that
$Q=V^T D V$
with V and D as above, we obtain that
We count the number of solutions of
![]() $q(x) =n$
. For
$q(x) =n$
. For
![]() $x_3,\ldots,x_{m}$
there are at most
$x_3,\ldots,x_{m}$
there are at most
 \begin{align*}\left(2 \sqrt{\frac{2n}{a_3}}+1\right) \cdots \left(2 \sqrt{\frac{2n}{a_{m}}}+1\right)\end{align*}
\begin{align*}\left(2 \sqrt{\frac{2n}{a_3}}+1\right) \cdots \left(2 \sqrt{\frac{2n}{a_{m}}}+1\right)\end{align*}
choices. After that, we are left with a binary problem that has
![]() $\mathcal{O}(n^{{\epsilon}})$
solutions uniformly in all parameters, cf. [Reference Blomer and Pohl5, lemma 8(a)]. This yields
$\mathcal{O}(n^{{\epsilon}})$
solutions uniformly in all parameters, cf. [Reference Blomer and Pohl5, lemma 8(a)]. This yields
 \begin{align*}r(Q,n) \ll_m \left(1 + \frac{n^{1/2}}{\sqrt{a_3}}+ \cdots + \frac{n^{\frac{m}{2}-1}}{\sqrt{a_3\cdots a_{m}}} \right) n^{\epsilon}.\end{align*}
\begin{align*}r(Q,n) \ll_m \left(1 + \frac{n^{1/2}}{\sqrt{a_3}}+ \cdots + \frac{n^{\frac{m}{2}-1}}{\sqrt{a_3\cdots a_{m}}} \right) n^{\epsilon}.\end{align*}
If we want to count all solutions of
![]() $q(x) \leq l$
, we proceed as before, but bound the number of solutions for
$q(x) \leq l$
, we proceed as before, but bound the number of solutions for
![]() $x_1$
and
$x_1$
and
![]() $x_2$
by
$x_2$
by
![]() $\big(2\sqrt{{2l}/{a_1}} +1 \big) \text{ and } \big(2\sqrt{{2l}/{a_2}}+1\big).$
Thus, we obtain
$\big(2\sqrt{{2l}/{a_1}} +1 \big) \text{ and } \big(2\sqrt{{2l}/{a_2}}+1\big).$
Thus, we obtain
 \begin{align*}\sum_{x \leq l} r(Q,x) \ll 1 + \max_{1 \leq j \leq m} \frac{l^{\frac{j}{2}}}{ \sqrt{a_1} \ldots \sqrt{a_j}}.\end{align*}
\begin{align*}\sum_{x \leq l} r(Q,x) \ll 1 + \max_{1 \leq j \leq m} \frac{l^{\frac{j}{2}}}{ \sqrt{a_1} \ldots \sqrt{a_j}}.\end{align*}
Then, we obtain (16) by applying these bounds and using that
![]() $a_1 \cdots a_m = \det Q$
.
$a_1 \cdots a_m = \det Q$
.
Next, we consider the quadratic form corresponding to
![]() $NQ^{-1}$
. Note that
$NQ^{-1}$
. Note that
The diagonal entries of
![]() $ND^{-1}$
are
$ND^{-1}$
are
The lowest diagonal entry
![]() ${N}/{a_{m}}$
of D equals the lower right entries of
${N}/{a_{m}}$
of D equals the lower right entries of
![]() $N Q^{-1}$
since
$N Q^{-1}$
since
![]() $V^{-1}$
is an upper and
$V^{-1}$
is an upper and
![]() $V^{-T}$
a lower diagonal matrix with ones on the diagonal. Hence,
$V^{-T}$
a lower diagonal matrix with ones on the diagonal. Hence,
![]() ${N}{a_{m}} \in {\mathbb Z}$
and thus
${N}{a_{m}} \in {\mathbb Z}$
and thus
![]() $a_m \leq N$
. Together with
$a_m \leq N$
. Together with
![]() $a_i \geq 1$
and
$a_i \geq 1$
and
![]() $a_i \leq \frac{4}{3} a_{i+1}$
, this gives (15).
$a_i \leq \frac{4}{3} a_{i+1}$
, this gives (15).
Moreover, it holds that
 \begin{align*}\tilde{q}(x) &\,{:\!=}\, \frac{1}{2} x^T N Q^{-1} x =\frac{1}{2} x^T V^{-1} (N D^{-1}) V^{-T} x \\ &= \frac{N}{2 a_1} x_1^2 + \cdots + \frac{N}{2 a_m} ( w_{1,m} x_1 + \cdots + w_{m-1,m} x_{m-1}^2 + x_m)^2,\end{align*}
\begin{align*}\tilde{q}(x) &\,{:\!=}\, \frac{1}{2} x^T N Q^{-1} x =\frac{1}{2} x^T V^{-1} (N D^{-1}) V^{-T} x \\ &= \frac{N}{2 a_1} x_1^2 + \cdots + \frac{N}{2 a_m} ( w_{1,m} x_1 + \cdots + w_{m-1,m} x_{m-1}^2 + x_m)^2,\end{align*}
where
![]() $w_{ij}$
are the entries of
$w_{ij}$
are the entries of
![]() $V^{-1}$
. Their absolute value
$V^{-1}$
. Their absolute value
![]() $|w_{ij}|$
is bounded from above by a constant. To see this, write
$|w_{ij}|$
is bounded from above by a constant. To see this, write
![]() $V= I + M$
for the
$V= I + M$
for the
![]() $m\times m$
identity I and a nilpotent matrix M. Then, a simple calculation shows that
$m\times m$
identity I and a nilpotent matrix M. Then, a simple calculation shows that
![]() $V^{-1} = (I+M)^{-1} = I + \sum_{k=1}^{m-1} (\!-1)^k M^k$
.
$V^{-1} = (I+M)^{-1} = I + \sum_{k=1}^{m-1} (\!-1)^k M^k$
.
Next, we count solutions of
![]() $\tilde{q}(x) =n$
. For
$\tilde{q}(x) =n$
. For
![]() $x_1,\cdots x_{m-2}$
there are
$x_1,\cdots x_{m-2}$
there are
 \begin{equation*}\left(2 \sqrt{n\cdot \frac{ 2a_1}{N}}+1\right) \cdots \left(2 \sqrt{n \cdot \frac{ 2a_{m-2}}{N}}+1 \right)\end{equation*}
\begin{equation*}\left(2 \sqrt{n\cdot \frac{ 2a_1}{N}}+1\right) \cdots \left(2 \sqrt{n \cdot \frac{ 2a_{m-2}}{N}}+1 \right)\end{equation*}
choices and
![]() $\mathcal{O}(n^{\epsilon})$
for
$\mathcal{O}(n^{\epsilon})$
for
![]() $x_{m-1} $
and
$x_{m-1} $
and
![]() $x_m$
. It follows that
$x_m$
. It follows that
 \begin{align} r(NQ^{-1},n) \ll \left(1 + \frac{n^{1/2} \sqrt{a_{m-2}}}{\sqrt{N}}+ \cdots + \frac{n^{\frac{m}{2}-1}\sqrt{a_1 \cdots a_{m-2} }}{N^{\frac{m}{2}-1}} \right) n^{\epsilon}.\end{align}
\begin{align} r(NQ^{-1},n) \ll \left(1 + \frac{n^{1/2} \sqrt{a_{m-2}}}{\sqrt{N}}+ \cdots + \frac{n^{\frac{m}{2}-1}\sqrt{a_1 \cdots a_{m-2} }}{N^{\frac{m}{2}-1}} \right) n^{\epsilon}.\end{align}
Moreover, we obtain by the same argument as above that
Combining these bounds yields the last claim.
The level of a form is easily determinable by the local splittings:
Lemma 10. Let
![]() $q= x^T Q x/2$
be equivalent over
$q= x^T Q x/2$
be equivalent over
![]() ${\mathbb Z}_p$
to (4) for odd p and to (5) for
${\mathbb Z}_p$
to (4) for odd p and to (5) for
![]() $p=2$
. Set
$p=2$
. Set
Then, the level N of Q is given by
![]() $N = \prod_{p} p^{\nu(p)}$
.
$N = \prod_{p} p^{\nu(p)}$
.
Proof. For odd p, choose
![]() $U \in \textrm{GL}_m({\mathbb Z}_p)$
such that
$U \in \textrm{GL}_m({\mathbb Z}_p)$
such that
![]() $\tilde{Q} = U^T Q U$
is diagonal with entries
$\tilde{Q} = U^T Q U$
is diagonal with entries
![]() $u_i p^{\nu_i(p)}$
. It follows that
$u_i p^{\nu_i(p)}$
. It follows that
![]() $N \tilde{Q}^{-1} = U^{-1} N Q^{-1} U^{-T}$
, thus
$N \tilde{Q}^{-1} = U^{-1} N Q^{-1} U^{-T}$
, thus
![]() $p^{\nu_i(p)} \mid N$
for all p. For the other inclusion, we ise that every entry of
$p^{\nu_i(p)} \mid N$
for all p. For the other inclusion, we ise that every entry of
![]() $p^{\nu(p)} Q^{-1} = U^{-1} p^{\nu(p)} \tilde{Q}^{-1} U^{-T}$
is in
$p^{\nu(p)} Q^{-1} = U^{-1} p^{\nu(p)} \tilde{Q}^{-1} U^{-T}$
is in
![]() ${\mathbb Z}_p \cap {\mathbb Q} = \{{a}/{b} \in {\mathbb Q} \mid p \nmid b \}$
. For
${\mathbb Z}_p \cap {\mathbb Q} = \{{a}/{b} \in {\mathbb Q} \mid p \nmid b \}$
. For
![]() $p=2$
, we choose
$p=2$
, we choose
![]() $U \in \textrm{GL}_m({\mathbb Z}_2)$
such that
$U \in \textrm{GL}_m({\mathbb Z}_2)$
such that
![]() $\tilde{Q} = U^T Q U$
is of the form (5). By
$\tilde{Q} = U^T Q U$
is of the form (5). By
and the same argument as before, the claim follows
To evaluate the Fourier coefficients of
![]() $\theta(Q,z)|\left(\begin{smallmatrix}a & b \\ c & d\end{smallmatrix}\right)$
, we construct a diagonal matrix D that depends on Q and c. To this end, let
$\theta(Q,z)|\left(\begin{smallmatrix}a & b \\ c & d\end{smallmatrix}\right)$
, we construct a diagonal matrix D that depends on Q and c. To this end, let
![]() $c= \tilde{c} 2^t$
for odd
$c= \tilde{c} 2^t$
for odd
![]() $\tilde{c}$
and fix
$\tilde{c}$
and fix
![]() $U \in \textrm{SL}_m({\mathbb Z})$
such that
$U \in \textrm{SL}_m({\mathbb Z})$
such that
![]() $x^T U^T Q U x/2 \equiv \sum_{i=1}^m q_i x_i^2 \,(\textrm{mod}\ \tilde{c})$
and
$x^T U^T Q U x/2 \equiv \sum_{i=1}^m q_i x_i^2 \,(\textrm{mod}\ \tilde{c})$
and
 \begin{align*}\frac{1}{2}x^T U^T Q U x \equiv \sum_{i=1}^{r} 2^{\tilde{\nu}_i} g_i(x_{2i-1}, x_{2i})+ \sum_{i=2r+1}^m 2^{\nu_i} u_i x_i^2 ~(\textrm{mod}\ 2^t)\end{align*}
\begin{align*}\frac{1}{2}x^T U^T Q U x \equiv \sum_{i=1}^{r} 2^{\tilde{\nu}_i} g_i(x_{2i-1}, x_{2i})+ \sum_{i=2r+1}^m 2^{\nu_i} u_i x_i^2 ~(\textrm{mod}\ 2^t)\end{align*}
for odd
![]() $u_i \in {\mathbb Z}$
and
$u_i \in {\mathbb Z}$
and
![]() $g_i(x_{2i-1}, x_{2i}) = (x_{2i-1}^2 + x_{2i-1} x_{2i} + x_{2i}^2)$
or
$g_i(x_{2i-1}, x_{2i}) = (x_{2i-1}^2 + x_{2i-1} x_{2i} + x_{2i}^2)$
or
![]() $x_{2i-1} x_{2i}$
,
$x_{2i-1} x_{2i}$
,
![]() $\tilde{\nu}_i,\nu_i \le t$
. We set
$\tilde{\nu}_i,\nu_i \le t$
. We set
![]() $\tilde{d}_i = (q_i,\tilde{c},N)$
,
$\tilde{d}_i = (q_i,\tilde{c},N)$
,
![]() $t_{2i-1} = t_{2i} = \tilde{\nu}_i$
for
$t_{2i-1} = t_{2i} = \tilde{\nu}_i$
for
![]() $i \leq r$
,
$i \leq r$
,
 \begin{align*}t_i = \begin{cases} \nu_i & t \leq \nu_i +1, \\ \\[-7pt] \nu_i +1 & t \geq \nu_i +2, \end{cases} \text{ for } i > 2r \text{ and } D \,{:\!=}\, \textrm{diag}\ (\tilde{d}_1 2^{t_1} ,\ldots,\tilde{d}_m 2^{t_m} ).\end{align*}
\begin{align*}t_i = \begin{cases} \nu_i & t \leq \nu_i +1, \\ \\[-7pt] \nu_i +1 & t \geq \nu_i +2, \end{cases} \text{ for } i > 2r \text{ and } D \,{:\!=}\, \textrm{diag}\ (\tilde{d}_1 2^{t_1} ,\ldots,\tilde{d}_m 2^{t_m} ).\end{align*}
Furthermore, we set
![]() $\eta = \eta(Q,t) \,{:\!=}\, \#\{ i > 2r \mid t > \nu_i \}$
,
$\eta = \eta(Q,t) \,{:\!=}\, \#\{ i > 2r \mid t > \nu_i \}$
,
![]() $\kern3pt\hat{\kern-3pt d} \,{:\!=}\, d/2$
if
$\kern3pt\hat{\kern-3pt d} \,{:\!=}\, d/2$
if
![]() $2^2 \mid\!\mid N, 2 \mid\!\mid d$
and
$2^2 \mid\!\mid N, 2 \mid\!\mid d$
and
![]() $2r<m$
and
$2r<m$
and
![]() $\kern3pt\hat{\kern-3pt d}=d$
otherwise. Moreover, let
$\kern3pt\hat{\kern-3pt d}=d$
otherwise. Moreover, let
![]() $u_i$
denote the i-th column of U and
$u_i$
denote the i-th column of U and
![]() $\tilde{x}_i \,{:\!=}\, {u_i^T x}/{2^{\nu_i}} \in {\mathbb Z}$
. Then, we set
$\tilde{x}_i \,{:\!=}\, {u_i^T x}/{2^{\nu_i}} \in {\mathbb Z}$
. Then, we set
![]() $\delta(x) =0$
if there is
$\delta(x) =0$
if there is
![]() $i>2r$
such that
$i>2r$
such that
![]() $\tilde{x}_i$
is even and
$\tilde{x}_i$
is even and
![]() $t=\nu_i+1$
or
$t=\nu_i+1$
or
![]() $\tilde{x}_i$
is odd and
$\tilde{x}_i$
is odd and
![]() $t > \nu_i+2$
. In all other cases, we put
$t > \nu_i+2$
. In all other cases, we put
![]() $\delta(x)=1$
.
$\delta(x)=1$
.
Lemma 11. Let U, D as above and set
![]() $\tilde{Q} = U^T Q U$
. Then
$\tilde{Q} = U^T Q U$
. Then
![]() $\frac{N}{\kern3pt\hat{\kern-3pt d}} D \tilde{Q}^{-1} D$
corresponds to a positive, integral quadratic form of level
$\frac{N}{\kern3pt\hat{\kern-3pt d}} D \tilde{Q}^{-1} D$
corresponds to a positive, integral quadratic form of level
![]() $\le N$
.
$\le N$
.
Proof. By construction
![]() $2 D^{-1} \tilde{Q}$
corresponds to a positive, integral quadratic form. Over
$2 D^{-1} \tilde{Q}$
corresponds to a positive, integral quadratic form. Over
![]() ${\mathbb Z}_p$
and p odd,
${\mathbb Z}_p$
and p odd,
![]() $q= x^T D^{-1} \tilde{Q} x$
is equivalent to
$q= x^T D^{-1} \tilde{Q} x$
is equivalent to
![]() $\tilde{u}_1 \frac{p^{\nu_1}}{(p^{\nu_1},\,d)} x_1^2 + \cdots + \tilde{u}_m \frac{p^{\nu_m}}{(p^{\nu_m},\,d)} x_m^2.$
Over
$\tilde{u}_1 \frac{p^{\nu_1}}{(p^{\nu_1},\,d)} x_1^2 + \cdots + \tilde{u}_m \frac{p^{\nu_m}}{(p^{\nu_m},\,d)} x_m^2.$
Over
![]() ${\mathbb Z}_2$
, q is equivalent to
${\mathbb Z}_2$
, q is equivalent to
 \begin{align*}\sum_{i=1}^{r_2} 2^{\nu_{i}+1 -t_i} g(x_{2i-1},x_{2i})+ \sum_{i=2r_2+1}^m 2^{\nu_{i}+1 -t_i}u_i x_i^2,\end{align*}
\begin{align*}\sum_{i=1}^{r_2} 2^{\nu_{i}+1 -t_i} g(x_{2i-1},x_{2i})+ \sum_{i=2r_2+1}^m 2^{\nu_{i}+1 -t_i}u_i x_i^2,\end{align*}
By Lemma 10, this implies that
![]() $2 D^{-1} \tilde{Q}$
has level
$2 D^{-1} \tilde{Q}$
has level
![]() $4{N}/{d}$
if the maximum of
$4{N}/{d}$
if the maximum of
![]() $2^{\nu_{i}+1 -t_i} + 2 \delta_{i> 2r}$
is attained for
$2^{\nu_{i}+1 -t_i} + 2 \delta_{i> 2r}$
is attained for
![]() $i>2r$
and
$i>2r$
and
![]() $t = \nu_i+1$
and
$t = \nu_i+1$
and
![]() $2{N}/{d}$
otherwise. Hence,
$2{N}/{d}$
otherwise. Hence,
![]() ${N}D \tilde{Q}^{-1} D/d$
has even diagonal entries unless
${N}D \tilde{Q}^{-1} D/d$
has even diagonal entries unless
![]() $2^2 \mid\!\mid N, 2 \mid\!\mid d$
and
$2^2 \mid\!\mid N, 2 \mid\!\mid d$
and
![]() $2r < m$
.
$2r < m$
.
For simplicity, we omit the weight
![]() ${m}/{2}$
in the slash operator
${m}/{2}$
in the slash operator
![]() $|[\varrho]_{\frac{m}{2}}$
.
$|[\varrho]_{\frac{m}{2}}$
.
Lemma 12. Let
![]() $\varrho = \left(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\right) \in \textrm{SL}_2({\mathbb Z})$
, with
$\varrho = \left(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\right) \in \textrm{SL}_2({\mathbb Z})$
, with
![]() $\varrho \notin \Gamma_0(N)$
. Moreover, let
$\varrho \notin \Gamma_0(N)$
. Moreover, let
![]() $D, \eta, \delta(x)$
and
$D, \eta, \delta(x)$
and
![]() $\kern3pt\hat{\kern-3pt d}$
as above Lemma 11 and
$\kern3pt\hat{\kern-3pt d}$
as above Lemma 11 and
![]() $\tilde{Q}$
as in Lemma 11. Then,
$\tilde{Q}$
as in Lemma 11. Then,
 \begin{align*}\theta(Q,z)|[\varrho] = \frac{\sqrt{2^\eta \det D}}{\sqrt{\det Q}} \sum_{x \in {\mathbb Z}^{m}} \delta(x) \omega e\left(\frac{1}{2} x^T D \tilde{Q}^{-1} D x z\right),\end{align*}
\begin{align*}\theta(Q,z)|[\varrho] = \frac{\sqrt{2^\eta \det D}}{\sqrt{\det Q}} \sum_{x \in {\mathbb Z}^{m}} \delta(x) \omega e\left(\frac{1}{2} x^T D \tilde{Q}^{-1} D x z\right),\end{align*}
for some
![]() $|\omega|=1$
. For
$|\omega|=1$
. For
![]() $S \,{:\!=}\, \frac{N}{\kern3pt\hat{\kern-3pt d}}D \tilde{Q}^{-1} D$
, it follows that
$S \,{:\!=}\, \frac{N}{\kern3pt\hat{\kern-3pt d}}D \tilde{Q}^{-1} D$
, it follows that
 \begin{align*}\theta(Q,z)|[\varrho] = \sum_{n \geq 0} a(n) e\left(\frac{\kern3pt\hat{\kern-3pt d} nz}{N}\right) \text{ with } |a(n)|\leq 2^{\frac{m}{2}} \frac{\sqrt{\det D }}{\sqrt{\det Q}} r(S,n).\end{align*}
\begin{align*}\theta(Q,z)|[\varrho] = \sum_{n \geq 0} a(n) e\left(\frac{\kern3pt\hat{\kern-3pt d} nz}{N}\right) \text{ with } |a(n)|\leq 2^{\frac{m}{2}} \frac{\sqrt{\det D }}{\sqrt{\det Q}} r(S,n).\end{align*}
If
![]() $d=(c,N)=1$
, we have that
$d=(c,N)=1$
, we have that
![]() $|a(n)| = {r(NQ^{-1})}/{\sqrt{\det Q}}$
.
$|a(n)| = {r(NQ^{-1})}/{\sqrt{\det Q}}$
.
Proof. By the factorisation
![]() $ \varrho = \left(\begin{smallmatrix} 1 & a / c \\ & 1 \end{smallmatrix}\right) \left(\begin{smallmatrix} & - 1 / c \\ c \end{smallmatrix}\right)\left( \begin{smallmatrix} 1 & d / c \\ & 1 \end{smallmatrix}\right)$
and the transformation formula for the generalised theta series, cf. [Reference Siegel27, p. 575], we get that
$ \varrho = \left(\begin{smallmatrix} 1 & a / c \\ & 1 \end{smallmatrix}\right) \left(\begin{smallmatrix} & - 1 / c \\ c \end{smallmatrix}\right)\left( \begin{smallmatrix} 1 & d / c \\ & 1 \end{smallmatrix}\right)$
and the transformation formula for the generalised theta series, cf. [Reference Siegel27, p. 575], we get that
where
 \begin{align} \alpha(x,Q,\varrho) = \frac{e\left(\frac{3m}{8}\right)}{c^{\frac{m}{2}} \sqrt{\det Q}} e\left(\frac{d}{2 c} x^T Q^{-1} x\right) \sum_{v \in ({\mathbb Z}/c{\mathbb Z})^{m}} e \left(\frac{1}{c} v^T x + \frac{a}{2 c}v^T Q v\right). \end{align}
\begin{align} \alpha(x,Q,\varrho) = \frac{e\left(\frac{3m}{8}\right)}{c^{\frac{m}{2}} \sqrt{\det Q}} e\left(\frac{d}{2 c} x^T Q^{-1} x\right) \sum_{v \in ({\mathbb Z}/c{\mathbb Z})^{m}} e \left(\frac{1}{c} v^T x + \frac{a}{2 c}v^T Q v\right). \end{align}
We write
![]() $c = \tilde{c} \, 2^t$
with odd
$c = \tilde{c} \, 2^t$
with odd
![]() $\tilde{c}$
and decompose this sum into
$\tilde{c}$
and decompose this sum into
 \begin{align*} \sum_{v \in ({\mathbb Z}/\tilde{c}{\mathbb Z})^{m}} e \left(\frac{a 2^{t} \frac{1}{2} v^T Q v + v^Tx}{\tilde{c}} \right) \sum_{w \in ({\mathbb Z}/2^t{\mathbb Z})^{m}} e \left(\frac{a \tilde{c} \frac{1}{2} w^T Q w + w^Tx}{2^t} \right). \end{align*}
\begin{align*} \sum_{v \in ({\mathbb Z}/\tilde{c}{\mathbb Z})^{m}} e \left(\frac{a 2^{t} \frac{1}{2} v^T Q v + v^Tx}{\tilde{c}} \right) \sum_{w \in ({\mathbb Z}/2^t{\mathbb Z})^{m}} e \left(\frac{a \tilde{c} \frac{1}{2} w^T Q w + w^Tx}{2^t} \right). \end{align*}
Next, we choose
![]() $U \in \textrm{SL}_m({\mathbb Z})$
as in Lemma 11 and substitute v, w by Uv, Uw. Since
$U \in \textrm{SL}_m({\mathbb Z})$
as in Lemma 11 and substitute v, w by Uv, Uw. Since
![]() $ v^TU^TQUv/2 \equiv \sum_{i=1}^m q_i v_i^2 \,(\textrm{mod}\ \tilde{c})$
we obtain for
$ v^TU^TQUv/2 \equiv \sum_{i=1}^m q_i v_i^2 \,(\textrm{mod}\ \tilde{c})$
we obtain for
![]() $G(a,b,c) \,{:\!=}\, \sum_{x\textrm{mod}\ c} e\Big(({ax^2+bx})/{c}\Big)$
that
$G(a,b,c) \,{:\!=}\, \sum_{x\textrm{mod}\ c} e\Big(({ax^2+bx})/{c}\Big)$
that
 \begin{align*} \sum_{v \in ({\mathbb Z}/\tilde{c}{\mathbb Z})^{m}} e \left(\frac{a 2^{t} \frac{1}{2} v^T Q v + v^Tx}{\tilde{c}} \right) = \prod_{i=1}^m G(q_i a 2^t,u_i^Tx,\tilde{c}),\end{align*}
\begin{align*} \sum_{v \in ({\mathbb Z}/\tilde{c}{\mathbb Z})^{m}} e \left(\frac{a 2^{t} \frac{1}{2} v^T Q v + v^Tx}{\tilde{c}} \right) = \prod_{i=1}^m G(q_i a 2^t,u_i^Tx,\tilde{c}),\end{align*}
where
![]() $u_i$
denotes the i-th column of U. The i-th sum vanishes unless
$u_i$
denotes the i-th column of U. The i-th sum vanishes unless
![]() $d_i \mid u_i^T x$
for
$d_i \mid u_i^T x$
for
![]() $d_i \,{:\!=}\, (\tilde{c},q_i)$
. By completing the square, the previous display equals
$d_i \,{:\!=}\, (\tilde{c},q_i)$
. By completing the square, the previous display equals
 \begin{align} \tilde{c}^\frac{m}{2} {\epsilon}_{\tilde{c}}^m \prod_{i=1}^m \sqrt{\tilde{d}_i} \left(\frac{a 2^t \tilde{q}_i }{\tilde{c}_i}\right) e\Big(\!-\frac{\overline{ 2^{t+2} a \tilde{q}_i} \tilde{x}_i^2}{\tilde{c}_i}\Big), \end{align}
\begin{align} \tilde{c}^\frac{m}{2} {\epsilon}_{\tilde{c}}^m \prod_{i=1}^m \sqrt{\tilde{d}_i} \left(\frac{a 2^t \tilde{q}_i }{\tilde{c}_i}\right) e\Big(\!-\frac{\overline{ 2^{t+2} a \tilde{q}_i} \tilde{x}_i^2}{\tilde{c}_i}\Big), \end{align}
where
![]() $\tilde{q}_i = q_i / d_i, \tilde{c}_i = \tilde{c}/d_i$
and
$\tilde{q}_i = q_i / d_i, \tilde{c}_i = \tilde{c}/d_i$
and
![]() $\tilde{x}_i=u_i^T x / d_i$
. The absolute value of the term above is
$\tilde{x}_i=u_i^T x / d_i$
. The absolute value of the term above is
![]() $\tilde{c}^\frac{m}{2} \sqrt{\tilde{d}_1} \cdots \sqrt{\tilde{d}_m}$
. Furthermore, we have for U as in Lemma 11 that
$\tilde{c}^\frac{m}{2} \sqrt{\tilde{d}_1} \cdots \sqrt{\tilde{d}_m}$
. Furthermore, we have for U as in Lemma 11 that
 \begin{align*} \frac{1}{2}x^TU^TQUx \equiv \sum_{i=1}^{r_1} 2^{\tilde{\nu}_i} g(x_{2i-1},x_{2i}) + \sum_{i=r_1+1}^{r_2} 2^{\tilde{\nu}_i} x_{2i-1} x_{2i} + \sum_{i=2r_2+1}^m 2^{\nu_i} b_i x_i^2 \,(\textrm{mod}\ 2^t), \end{align*}
\begin{align*} \frac{1}{2}x^TU^TQUx \equiv \sum_{i=1}^{r_1} 2^{\tilde{\nu}_i} g(x_{2i-1},x_{2i}) + \sum_{i=r_1+1}^{r_2} 2^{\tilde{\nu}_i} x_{2i-1} x_{2i} + \sum_{i=2r_2+1}^m 2^{\nu_i} b_i x_i^2 \,(\textrm{mod}\ 2^t), \end{align*}
where
![]() $b_i$
are odd integers,
$b_i$
are odd integers,
![]() $0\leq 2r_1 \leq 2r_2 \leq m$
,
$0\leq 2r_1 \leq 2r_2 \leq m$
,
![]() $g(x_{2i-1},x_{2i}) = x_{2i-1}^2 + x_{2i-1}x_{2i} + x_{2i}^2$
and
$g(x_{2i-1},x_{2i}) = x_{2i-1}^2 + x_{2i-1}x_{2i} + x_{2i}^2$
and
![]() $\tilde{\nu_i},\nu_i \leq t$
. For
$\tilde{\nu_i},\nu_i \leq t$
. For
![]() $i > 2r_2$
, we need to evaluate
$i > 2r_2$
, we need to evaluate
![]() $ G(2^{\nu_i} b_i a \tilde{c}, u_i^T x, 2^t )$
which vanishes unless
$ G(2^{\nu_i} b_i a \tilde{c}, u_i^T x, 2^t )$
which vanishes unless
![]() $u_i^T x \equiv 0\,( \textrm{mod}\ 2^{\nu_i})$
. For
$u_i^T x \equiv 0\,( \textrm{mod}\ 2^{\nu_i})$
. For
![]() $\tilde{x}_i ={u_i^T x}/{2^{\nu_i}}$
, this sum
$\tilde{x}_i ={u_i^T x}/{2^{\nu_i}}$
, this sum
![]() $G(2^{\nu_i} b_i a \tilde{c}, u_i^T x, 2^t )$
equals
$G(2^{\nu_i} b_i a \tilde{c}, u_i^T x, 2^t )$
equals
 \begin{align*} 2^{\nu_i} G(b_ia \tilde{c},\tilde{x_i},2^{t-\nu_i})= \begin{cases} 2{\dfrac{\nu_i+t}{2}} & t= \nu_i, \\ \\[-8pt] 2{\dfrac{\nu_i+t+1}{2}} \delta_{\tilde{x}_i \equiv 1 \,(\textrm{mod}\ 2)} & t = \nu_i+1, \\ \\[-8pt] 2{\dfrac{\nu_i+t+1}{2}} \omega e\Big(\frac{-\overline{b_i a \tilde{c}} (\tilde{x}_i/2)^2}{2^{t-\nu_i}}\Big) \delta_{\tilde{x}_i \,{\equiv}\,0\, (\textrm{mod}\ 2)} & t \geq \nu_i +2, \end{cases} \end{align*}
\begin{align*} 2^{\nu_i} G(b_ia \tilde{c},\tilde{x_i},2^{t-\nu_i})= \begin{cases} 2{\dfrac{\nu_i+t}{2}} & t= \nu_i, \\ \\[-8pt] 2{\dfrac{\nu_i+t+1}{2}} \delta_{\tilde{x}_i \equiv 1 \,(\textrm{mod}\ 2)} & t = \nu_i+1, \\ \\[-8pt] 2{\dfrac{\nu_i+t+1}{2}} \omega e\Big(\frac{-\overline{b_i a \tilde{c}} (\tilde{x}_i/2)^2}{2^{t-\nu_i}}\Big) \delta_{\tilde{x}_i \,{\equiv}\,0\, (\textrm{mod}\ 2)} & t \geq \nu_i +2, \end{cases} \end{align*}
where
![]() $\omega \,{:\!=}\, {\epsilon}_{ b_i a \tilde{c}}^{-1} \left({2^{t-\nu_i}}/{b_i a \tilde{c}}\right) e(1/8)$
. For forms of type
$\omega \,{:\!=}\, {\epsilon}_{ b_i a \tilde{c}}^{-1} \left({2^{t-\nu_i}}/{b_i a \tilde{c}}\right) e(1/8)$
. For forms of type
![]() $2^{\tilde{\nu}} (x_1^2 + x_1 x_2 +x_2^2)$
, we have that
$2^{\tilde{\nu}} (x_1^2 + x_1 x_2 +x_2^2)$
, we have that
 \begin{align} \sum_{w_1 (\textrm{mod}\ 2^{t})} e\left( \frac{ w_1^2 a \tilde{c} 2^{\tilde{\nu}} + w_1 u_1^T x_1}{2^t} \right) &\sum_{w_2 (\textrm{mod}\ 2^{t})} e\left( \frac{ w_2^2 a \tilde{c} 2^{\tilde{\nu}} + w_2 \left(u_1^T x_1 + a \tilde{c} 2^{\tilde{\nu}} w_1\right)}{2^t} \right) \end{align}
\begin{align} \sum_{w_1 (\textrm{mod}\ 2^{t})} e\left( \frac{ w_1^2 a \tilde{c} 2^{\tilde{\nu}} + w_1 u_1^T x_1}{2^t} \right) &\sum_{w_2 (\textrm{mod}\ 2^{t})} e\left( \frac{ w_2^2 a \tilde{c} 2^{\tilde{\nu}} + w_2 \left(u_1^T x_1 + a \tilde{c} 2^{\tilde{\nu}} w_1\right)}{2^t} \right) \end{align}
 \begin{align} \notag&= 2^{\tilde{\nu}+t} \zeta e\left(\frac{\overline{3a \tilde{c}} \left(\tilde{x}_1^2 - \tilde{x}_1 \tilde{x}_2 +\tilde{x}_2^2 \right)}{2^{t-\tilde{\nu}}}\right) \delta_{ \tilde{x}_1 \in {\mathbb Z}, \tilde{x}_2 \in {\mathbb Z}}\end{align}
\begin{align} \notag&= 2^{\tilde{\nu}+t} \zeta e\left(\frac{\overline{3a \tilde{c}} \left(\tilde{x}_1^2 - \tilde{x}_1 \tilde{x}_2 +\tilde{x}_2^2 \right)}{2^{t-\tilde{\nu}}}\right) \delta_{ \tilde{x}_1 \in {\mathbb Z}, \tilde{x}_2 \in {\mathbb Z}}\end{align}
where
![]() $\tilde{x}_i \,{:\!=}\, {u_i^T x}/{2^{\tilde{\nu}}}$
and
$\tilde{x}_i \,{:\!=}\, {u_i^T x}/{2^{\tilde{\nu}}}$
and
![]() $\zeta$
is a root of unity that does not depend on x.
$\zeta$
is a root of unity that does not depend on x.
For
![]() $t= \tilde{\nu}$
the claim is obvious. If
$t= \tilde{\nu}$
the claim is obvious. If
![]() $t = \tilde{\nu}+1$
, the latter sum vanishes unless
$t = \tilde{\nu}+1$
, the latter sum vanishes unless
![]() $\tilde{x}_2 + a \tilde{c} w_1$
is odd and (21) equals
$\tilde{x}_2 + a \tilde{c} w_1$
is odd and (21) equals
 \begin{align*}2^{\tilde{\nu}+t} e\left(\frac{\overline{a \tilde{c}} (\tilde{x}_1^2 - \tilde{x}_1 \tilde{x}_2 + \tilde{x}_2^2)}{2}\right).\end{align*}
\begin{align*}2^{\tilde{\nu}+t} e\left(\frac{\overline{a \tilde{c}} (\tilde{x}_1^2 - \tilde{x}_1 \tilde{x}_2 + \tilde{x}_2^2)}{2}\right).\end{align*}
If
![]() $t \geq \tilde{\nu}+2$
, the second sum vanishes unless
$t \geq \tilde{\nu}+2$
, the second sum vanishes unless
![]() $\tilde{x}_1 + a \tilde{c} w_1$
is even. In this case (21) equals
$\tilde{x}_1 + a \tilde{c} w_1$
is even. In this case (21) equals
 \begin{align*}2^{\frac{3\tilde{\nu}+t+1}{2}} &\omega \sum_{w_1 (\textrm{mod}\ 2^{t-\tilde{\nu}-1})} e\left(\frac{(2 w_1 - \overline{a \tilde{c}} \tilde{x}_2)^2 a \tilde{c} + (2 w_1 - \overline{a \tilde{c}} ) \tilde{x}_1 - a v_1^2}{2^{t-\tilde{\nu}}} \right) \\[3pt] &= 2^{\frac{3\tilde{\nu}+t-1}{2}} \omega e\left(\frac{\overline{a \tilde{c}} \left(\!-\tilde{x}_2^2+ \tilde{x}_1 \tilde{x}_2\right)}{2^{t-\tilde{\nu}}}\right) G(3a\tilde{c},2(2\tilde{x}_2-\tilde{x}_1),2^{t-\nu}) \\[3pt] &= 2^{\tilde{\nu}+t} \zeta e\left(\frac{\overline{3a \tilde{c}} \left(\tilde{x}_1^2 - \tilde{x}_1 \tilde{x}_2 +\tilde{x}_2^2 \right)}{2^{t-\tilde{\nu}}}\right).\end{align*}
\begin{align*}2^{\frac{3\tilde{\nu}+t+1}{2}} &\omega \sum_{w_1 (\textrm{mod}\ 2^{t-\tilde{\nu}-1})} e\left(\frac{(2 w_1 - \overline{a \tilde{c}} \tilde{x}_2)^2 a \tilde{c} + (2 w_1 - \overline{a \tilde{c}} ) \tilde{x}_1 - a v_1^2}{2^{t-\tilde{\nu}}} \right) \\[3pt] &= 2^{\frac{3\tilde{\nu}+t-1}{2}} \omega e\left(\frac{\overline{a \tilde{c}} \left(\!-\tilde{x}_2^2+ \tilde{x}_1 \tilde{x}_2\right)}{2^{t-\tilde{\nu}}}\right) G(3a\tilde{c},2(2\tilde{x}_2-\tilde{x}_1),2^{t-\nu}) \\[3pt] &= 2^{\tilde{\nu}+t} \zeta e\left(\frac{\overline{3a \tilde{c}} \left(\tilde{x}_1^2 - \tilde{x}_1 \tilde{x}_2 +\tilde{x}_2^2 \right)}{2^{t-\tilde{\nu}}}\right).\end{align*}
For forms of type
![]() $2^{\tilde{\nu}} x_{1} x_{2}$
we obtain by a simple computation
$2^{\tilde{\nu}} x_{1} x_{2}$
we obtain by a simple computation
 \begin{align} &\sum_{w_{1}(\textrm{mod}\ 2^t)} e\left(\frac{w_1 u_1^T x_{1}}{2^t} \right) \sum_{w_{2} (\textrm{mod}\ 2^t)} e\left(\frac{w_2 \left(u_2^T x_{2} + a w_1 2^{\tilde{\nu}}\right)}{2^{t}} \right) = 2^{t+\tilde{\nu}} e\left(\frac{\overline{a \tilde{c}} \tilde{x}_1 \tilde{x}_2}{2^{t-\nu}}\right)\end{align}
\begin{align} &\sum_{w_{1}(\textrm{mod}\ 2^t)} e\left(\frac{w_1 u_1^T x_{1}}{2^t} \right) \sum_{w_{2} (\textrm{mod}\ 2^t)} e\left(\frac{w_2 \left(u_2^T x_{2} + a w_1 2^{\tilde{\nu}}\right)}{2^{t}} \right) = 2^{t+\tilde{\nu}} e\left(\frac{\overline{a \tilde{c}} \tilde{x}_1 \tilde{x}_2}{2^{t-\nu}}\right)\end{align}
provided that
![]() $\tilde{x}_1, \tilde{x}_2 \in {\mathbb Z}$
.
$\tilde{x}_1, \tilde{x}_2 \in {\mathbb Z}$
.
It follows that
![]() $\alpha(x,Q,\varrho)$
vanishes unless
$\alpha(x,Q,\varrho)$
vanishes unless
![]() $D^{-1} U^T x \in {\mathbb Z}^m$
. If this holds, we have that
$D^{-1} U^T x \in {\mathbb Z}^m$
. If this holds, we have that
for some
![]() $\omega$
with
$\omega$
with
![]() $|{\omega}|=1$
. Substituting x by
$|{\omega}|=1$
. Substituting x by
![]() $U^{-T} D x$
in (18) yields the first claim of the lemma.
$U^{-T} D x$
in (18) yields the first claim of the lemma.
The absolute value of the n-th Fourier coefficient of
![]() $\theta|[\varrho](z) = \sum_n a(n) e(\kern3pt\hat{\kern-3pt d} nz/N)$
is given by
$\theta|[\varrho](z) = \sum_n a(n) e(\kern3pt\hat{\kern-3pt d} nz/N)$
is given by
 \begin{align*}|a(n)| = \left|\sum_{\frac{1}{2}x^T S x=n } \alpha(x,Q,\varrho)\right| \leq 2^{\frac{m}{2}}\frac{\sqrt{ \det D} }{\sqrt{\det Q}} r(S,n),\end{align*}
\begin{align*}|a(n)| = \left|\sum_{\frac{1}{2}x^T S x=n } \alpha(x,Q,\varrho)\right| \leq 2^{\frac{m}{2}}\frac{\sqrt{ \det D} }{\sqrt{\det Q}} r(S,n),\end{align*}
where
![]() $S\,{:\!=}\, \frac{N}{\kern3pt\hat{\kern-3pt d}} D \tilde{Q}^{-1}D$
. For
$S\,{:\!=}\, \frac{N}{\kern3pt\hat{\kern-3pt d}} D \tilde{Q}^{-1}D$
. For
![]() $d=(N,c)=1$
, we have that
$d=(N,c)=1$
, we have that
![]() $\eta= \delta(x)=1$
for all x. To prove
$\eta= \delta(x)=1$
for all x. To prove
![]() $|a(n)| = r(NQ^{-1}) / \sqrt{\det Q}$
, it remains to show that
$|a(n)| = r(NQ^{-1}) / \sqrt{\det Q}$
, it remains to show that
![]() $\alpha(x,Q,\varrho)$
only depends on n and not on the particular choice of x. By (19) it suffices to consider the Gauss sum modulo c. By (20), the dependence on x modulo
$\alpha(x,Q,\varrho)$
only depends on n and not on the particular choice of x. By (19) it suffices to consider the Gauss sum modulo c. By (20), the dependence on x modulo
![]() $\tilde{c}$
is given by
$\tilde{c}$
is given by
 \begin{align*} e\left(\!-\frac{\overline{2^{t+2}a} \sum_{i=1}^m \overline{q_i} \tilde{x}_i^2}{\tilde{c}} \right) = e\left(\!-\frac{n\overline{2^{2t+2}aN} }{\tilde{c}} \right). \end{align*}
\begin{align*} e\left(\!-\frac{\overline{2^{t+2}a} \sum_{i=1}^m \overline{q_i} \tilde{x}_i^2}{\tilde{c}} \right) = e\left(\!-\frac{n\overline{2^{2t+2}aN} }{\tilde{c}} \right). \end{align*}
For the last step, we use that
![]() $d_i=1$
and hence,
$d_i=1$
and hence,
![]() $U^TQU/2 = \textrm{diag}(q_1,\ldots,q_m)$
is invertible modulo
$U^TQU/2 = \textrm{diag}(q_1,\ldots,q_m)$
is invertible modulo
![]() $\tilde{c}$
which implies that
$\tilde{c}$
which implies that
![]() $n = x^T N Q^{-1} x/2 \equiv N \sum_{i=1}^m \overline{q_i} \tilde{x}_i^2 \,(\textrm{mod}\ \tilde{c})$
. If N is even, then c must be odd. If N is odd, then m must be even and there are no diagonal terms in the splitting over
$n = x^T N Q^{-1} x/2 \equiv N \sum_{i=1}^m \overline{q_i} \tilde{x}_i^2 \,(\textrm{mod}\ \tilde{c})$
. If N is even, then c must be odd. If N is odd, then m must be even and there are no diagonal terms in the splitting over
![]() ${\mathbb Z}_2$
. Since the inverse of
${\mathbb Z}_2$
. Since the inverse of
![]() $(\begin{smallmatrix} 2 & 1 \\ 1 & 2 \end{smallmatrix})$
modulo
$(\begin{smallmatrix} 2 & 1 \\ 1 & 2 \end{smallmatrix})$
modulo
![]() $2^t$
is given by
$2^t$
is given by
![]() $\overline{3} (\begin{smallmatrix} 2 & -1 \\ -1 & 2 \end{smallmatrix})$
we obtain that
$\overline{3} (\begin{smallmatrix} 2 & -1 \\ -1 & 2 \end{smallmatrix})$
we obtain that
 \begin{align*} n = \frac{1}{2} x^T N (U^T Q U)^{-1} x = N \sum_{i=1}^{r_1} \overline{3} \left(x_{2i-1}^2 - x_{2i-1} x_{2i} + x_{2i}^2\right) + N \sum_{i=1}^{r_1} x_{2i-1} x_{2i} \,(\textrm{mod}\ 2^t). \end{align*}
\begin{align*} n = \frac{1}{2} x^T N (U^T Q U)^{-1} x = N \sum_{i=1}^{r_1} \overline{3} \left(x_{2i-1}^2 - x_{2i-1} x_{2i} + x_{2i}^2\right) + N \sum_{i=1}^{r_1} x_{2i-1} x_{2i} \,(\textrm{mod}\ 2^t). \end{align*}
It follows by (21) and (22) that the dependence on x of the Gauss sum modulo
![]() $2^t$
is given by
$2^t$
is given by
![]() $e\Big(\!-{n\overline{\tilde{c}aN}}/{2^t} \Big)$
.
$e\Big(\!-{n\overline{\tilde{c}aN}}/{2^t} \Big)$
.
This provides the necessary tools to prove our main result:
Proof of Theorem 1 and 2. Both f and g are cusp forms since the value of
![]() $\theta(Q,z)$
at each cusp depends only on a genus-invariant term. Set
$\theta(Q,z)$
at each cusp depends only on a genus-invariant term. Set
![]() $\mu = [\textrm{SL}_2({\mathbb Z}) : \Gamma_{0}(N)]$
,
$\mu = [\textrm{SL}_2({\mathbb Z}) : \Gamma_{0}(N)]$
,
![]() $\tilde{\mu} = [\textrm{SL}_2({\mathbb Z}): \Gamma(N)]$
and recall that
$\tilde{\mu} = [\textrm{SL}_2({\mathbb Z}): \Gamma(N)]$
and recall that
 \begin{align*} \frac{\tilde{\mu}}{\mu} = N^2 \prod_{p \mid N } \left( {1- \frac{1}{p}} \right). \end{align*}
\begin{align*} \frac{\tilde{\mu}}{\mu} = N^2 \prod_{p \mid N } \left( {1- \frac{1}{p}} \right). \end{align*}
We obtain
 \begin{align*} \langle g,g \rangle = \int_{\Gamma_{0}(N) \backslash {\mathbb H}} |{g(z)}|^2 y^{\frac{m}{2}-2} dx\,dy = \frac{\mu}{\tilde{\mu}} \sum_{j=1}^{\tilde{\mu}} \int_{\textrm{SL}_2({\mathbb Z}) \backslash {\mathbb H}} \big|g|[\tau_j])(z)\big|^2 y^{\frac{m}{2}-2} dx\,dy \end{align*}
\begin{align*} \langle g,g \rangle = \int_{\Gamma_{0}(N) \backslash {\mathbb H}} |{g(z)}|^2 y^{\frac{m}{2}-2} dx\,dy = \frac{\mu}{\tilde{\mu}} \sum_{j=1}^{\tilde{\mu}} \int_{\textrm{SL}_2({\mathbb Z}) \backslash {\mathbb H}} \big|g|[\tau_j])(z)\big|^2 y^{\frac{m}{2}-2} dx\,dy \end{align*}
for a set of coset representatives
![]() $\tau_i$
of
$\tau_i$
of
![]() $\Gamma(N) \backslash \textrm{SL}_2({\mathbb Z})$
. On this set, we define an equivalence relation
$\Gamma(N) \backslash \textrm{SL}_2({\mathbb Z})$
. On this set, we define an equivalence relation
For the remaining matrices, a set of representatives is given by
For simplicity, we set
![]() $\varrho \,{:\!=}\, \varrho_{a,c}$
. It follows that
$\varrho \,{:\!=}\, \varrho_{a,c}$
. It follows that
 \begin{align} \langle g,g \rangle = \frac{\mu}{\tilde{\mu}} \sum_{c\, (\textrm{mod}\ N)} \sum_{\substack{a (\textrm{mod}\ N) \\ (a,c,N)=1}} \bigcup_{t \in T} \int_{t F} \big|g|[\varrho](z)\big|^2 y^{\frac{m}{2}-2} dx\,dy, \end{align}
\begin{align} \langle g,g \rangle = \frac{\mu}{\tilde{\mu}} \sum_{c\, (\textrm{mod}\ N)} \sum_{\substack{a (\textrm{mod}\ N) \\ (a,c,N)=1}} \bigcup_{t \in T} \int_{t F} \big|g|[\varrho](z)\big|^2 y^{\frac{m}{2}-2} dx\,dy, \end{align}
where
![]() $F = \{x+iy \mid - {1}/{2} \le x \le {1}/{2}, |x+iy| \geq 1 \}$
is a fundamental domain of
$F = \{x+iy \mid - {1}/{2} \le x \le {1}/{2}, |x+iy| \geq 1 \}$
is a fundamental domain of
![]() $\textrm{SL}_2({\mathbb Z}) \backslash {\mathbb H}$
. We put
$\textrm{SL}_2({\mathbb Z}) \backslash {\mathbb H}$
. We put
![]() $d=(c,N)$
and write
$d=(c,N)$
and write
![]() $g|[\varrho] = \sum_n a_{\varrho}(n) e\big({n \kern3pt\hat{\kern-3pt d} z}/{N} \big)$
for
$g|[\varrho] = \sum_n a_{\varrho}(n) e\big({n \kern3pt\hat{\kern-3pt d} z}/{N} \big)$
for
![]() $\kern3pt\hat{\kern-3pt d}$
either
$\kern3pt\hat{\kern-3pt d}$
either
![]() $d/2$
or d. By the previous display, it follows that
$d/2$
or d. By the previous display, it follows that
 \begin{align} \notag \langle g, g \rangle &\le N \frac{\mu }{\tilde{\mu}} \sum_{\substack{ c (\textrm{mod}\ N) \\ (c,N)=d}} \sum_{\substack{a (\textrm{mod}\ N) \\ (a,d)=1}} \int_{\frac{1}{2}}^{\infty} \sum_{n=1}^\infty |a_{\varrho}(n)|^2 \textrm{exp}\left(\!- \frac{2 \pi y n d}{N}\right) y^{\frac{m}{2}-2} dy \\[4pt] \notag &\ll N \frac{\mu }{\tilde{\mu}} \sum_{\substack{ c\, (\textrm{mod}\ N) \\ (c,N)=d}} \sum_{\substack{a (\textrm{mod}\ N) \\ (a,d)=1}} \Big(\frac{N}{d}\Big)^{\frac{m}{2}-1} \sum_{n \leq (N/d)^{1+{\epsilon}}} \frac{|a_{\varrho}(n)|^2}{n^{\frac{m}{2}-1}} + \mathcal{O}(N^{-100}). \end{align}
\begin{align} \notag \langle g, g \rangle &\le N \frac{\mu }{\tilde{\mu}} \sum_{\substack{ c (\textrm{mod}\ N) \\ (c,N)=d}} \sum_{\substack{a (\textrm{mod}\ N) \\ (a,d)=1}} \int_{\frac{1}{2}}^{\infty} \sum_{n=1}^\infty |a_{\varrho}(n)|^2 \textrm{exp}\left(\!- \frac{2 \pi y n d}{N}\right) y^{\frac{m}{2}-2} dy \\[4pt] \notag &\ll N \frac{\mu }{\tilde{\mu}} \sum_{\substack{ c\, (\textrm{mod}\ N) \\ (c,N)=d}} \sum_{\substack{a (\textrm{mod}\ N) \\ (a,d)=1}} \Big(\frac{N}{d}\Big)^{\frac{m}{2}-1} \sum_{n \leq (N/d)^{1+{\epsilon}}} \frac{|a_{\varrho}(n)|^2}{n^{\frac{m}{2}-1}} + \mathcal{O}(N^{-100}). \end{align}
For
![]() $c=0$
, we have
$c=0$
, we have
![]() $d=N$
and
$d=N$
and
![]() $a_\rho(n) = r(Q,n) - r(Q',n)$
. Hence, the contribution of this case is bounded by
$a_\rho(n) = r(Q,n) - r(Q',n)$
. Hence, the contribution of this case is bounded by
![]() $\mathcal{O}(N^{\epsilon})$
. For
$\mathcal{O}(N^{\epsilon})$
. For
![]() $c \neq 0$
we apply Lemma 12. This gives
$c \neq 0$
we apply Lemma 12. This gives
for matrices
![]() $D_\varrho, S_\varrho,\tilde{S}_\varrho$
given as in Lemma 12. Let
$D_\varrho, S_\varrho,\tilde{S}_\varrho$
given as in Lemma 12. Let
![]() $a'_1,\ldots,a'_m$
denote the associated diagonal entries of
$a'_1,\ldots,a'_m$
denote the associated diagonal entries of
![]() $S_\varrho$
. By Lemma 9 we infer that
$S_\varrho$
. By Lemma 9 we infer that
 \begin{align*} \sum_{n \le (N/d)^{1+{\epsilon}}} \frac{r(S_\varrho,n)^2}{n^{\frac{m}{2}-1}} &\ll \left( 1+ \sum_{j=m-1}^{2m-2} \Big(\frac{N}{d}\Big)^{\frac{j-m}{2}+1} \frac{\sqrt{a'_1 a'_2}}{\det S_d} \prod_{i=\lfloor \frac{j+5}{2}\rfloor}^m \sqrt{a'_i} \prod_{k=\lfloor \frac{j+4}{2}\rfloor}^m \sqrt{a'_k}\right) N^{\epsilon}. \end{align*}
\begin{align*} \sum_{n \le (N/d)^{1+{\epsilon}}} \frac{r(S_\varrho,n)^2}{n^{\frac{m}{2}-1}} &\ll \left( 1+ \sum_{j=m-1}^{2m-2} \Big(\frac{N}{d}\Big)^{\frac{j-m}{2}+1} \frac{\sqrt{a'_1 a'_2}}{\det S_d} \prod_{i=\lfloor \frac{j+5}{2}\rfloor}^m \sqrt{a'_i} \prod_{k=\lfloor \frac{j+4}{2}\rfloor}^m \sqrt{a'_k}\right) N^{\epsilon}. \end{align*}
To estimate this sum, we use
![]() $a'_1 a'_2 \ll (\det S_\varrho)^{\frac{2}{m}}$
and
$a'_1 a'_2 \ll (\det S_\varrho)^{\frac{2}{m}}$
and
![]() $a'_i \ll N$
for
$a'_i \ll N$
for
![]() $3 \le i \le m$
and
$3 \le i \le m$
and
![]() $\det S_\varrho = (N/d)^m (\det D_\varrho)^2 (\det Q)^{-1}$
. This yields that the j-th term is bounded by
$\det S_\varrho = (N/d)^m (\det D_\varrho)^2 (\det Q)^{-1}$
. This yields that the j-th term is bounded by
If m is even, we use that
![]() $a_i \gg 1$
and bound the
$a_i \gg 1$
and bound the
![]() $j=m-1$
term by
$j=m-1$
term by
 \begin{equation*}\frac{\sqrt{N}}{\sqrt{d}\sqrt{\det S_d}} \prod_{i=\frac{m}{2}+2}^{m} \sqrt{a'_i} \ll \frac{d^{\frac{m}{2}} N^{-\frac{m}{4}} \sqrt{\det Q}}{\det D_\varrho}.\end{equation*}
\begin{equation*}\frac{\sqrt{N}}{\sqrt{d}\sqrt{\det S_d}} \prod_{i=\frac{m}{2}+2}^{m} \sqrt{a'_i} \ll \frac{d^{\frac{m}{2}} N^{-\frac{m}{4}} \sqrt{\det Q}}{\det D_\varrho}.\end{equation*}
By construction,
![]() $\det D_\varrho$
only depends on
$\det D_\varrho$
only depends on
![]() $d=(c,N)$
. Since there are
$d=(c,N)$
. Since there are
![]() $\phi({N}/{d})$
choices for
$\phi({N}/{d})$
choices for
![]() $(c,N)=d$
and
$(c,N)=d$
and
![]() ${\phi(d)}/{d}N$
for a, it follows by the previous five displays that
${\phi(d)}/{d}N$
for a, it follows by the previous five displays that
 \begin{align} \langle g,g \rangle \ll N^{\epsilon} + \frac{N^\frac{m}{2}}{\det Q}\sum_{d \mid N} \frac{\det D_\varrho}{d^\frac{m}{2}} + \frac{N^{\frac{m}{4}}}{\sqrt{\det Q}}+\frac{N}{ \det Q^\frac{1}{m}} \sum_{d \mid N} \frac{d^{\lfloor\frac{m-3}{2}\rfloor}}{(\det D_\varrho)^{1-\frac{2}{m}}}.\end{align}
\begin{align} \langle g,g \rangle \ll N^{\epsilon} + \frac{N^\frac{m}{2}}{\det Q}\sum_{d \mid N} \frac{\det D_\varrho}{d^\frac{m}{2}} + \frac{N^{\frac{m}{4}}}{\sqrt{\det Q}}+\frac{N}{ \det Q^\frac{1}{m}} \sum_{d \mid N} \frac{d^{\lfloor\frac{m-3}{2}\rfloor}}{(\det D_\varrho)^{1-\frac{2}{m}}}.\end{align}
For the first d-sum, we use that
This bound is sharp for at least one d which can be constructed as follows. Let
![]() $v_p(j)$
defined as after (5), choose
$v_p(j)$
defined as after (5), choose
![]() $k_p$
maximal such that
$k_p$
maximal such that
![]() $v_{p}(k_p) \geq {m}/{2}$
and set
$v_{p}(k_p) \geq {m}/{2}$
and set
![]() $d= \prod_{p \mid N} p^{k_p}$
.
$d= \prod_{p \mid N} p^{k_p}$
.
By (24) and (25) we obtain the bound for
![]() $m=3$
and
$m=3$
and
![]() $m=4$
. For
$m=4$
. For
![]() $m \ge 5$
, we estimate
$m \ge 5$
, we estimate
 \begin{equation*}\frac{d^{\frac{m}{2}-\frac{3}{2}}}{(\det D_\varrho)^{1-\frac{2}{m}}} \le \frac{d^{\frac{m}{2}-\frac{3}{2}}}{F(D_\varrho,\frac{m-1}{2}-\frac{1}{m})^{1-\frac{2}{m}}} \le \frac{N^{\frac{m}{2}-1}}{F (Q,\frac{m-1}{2}-\frac{1}{m})^{1-\frac{1}{m}}}.\end{equation*}
\begin{equation*}\frac{d^{\frac{m}{2}-\frac{3}{2}}}{(\det D_\varrho)^{1-\frac{2}{m}}} \le \frac{d^{\frac{m}{2}-\frac{3}{2}}}{F(D_\varrho,\frac{m-1}{2}-\frac{1}{m})^{1-\frac{2}{m}}} \le \frac{N^{\frac{m}{2}-1}}{F (Q,\frac{m-1}{2}-\frac{1}{m})^{1-\frac{1}{m}}}.\end{equation*}
By definition, the same bounds hold for
![]() $\langle \,f,f \rangle$
. If Q is diagonal, we can do slightly better. The Fourier coefficients
$\langle \,f,f \rangle$
. If Q is diagonal, we can do slightly better. The Fourier coefficients
![]() $a_\varrho(n)$
of
$a_\varrho(n)$
of
![]() $(f|[\varrho])(z)$
are bounded by
$(f|[\varrho])(z)$
are bounded by
For the latter term, we make use of (14):
 \begin{align*} \frac{\det D_\varrho}{\det Q} \! \sum_{n \le (N/d)^{1+{\epsilon}}} \! \frac{r(\textrm{gen}\ S_\varrho,n)^2}{n^{\frac{m}{2}-1}} \ll \frac{d^m}{N^m \det D_\varrho } \! \sum_{n \le (N/d)^{1+{\epsilon}}} \! n^{\frac{m}{2}-1} (n,N) \ll \Big(\frac{N}{d}\Big)^{-\frac{m}{2}} N^{{\epsilon}}.\end{align*}
\begin{align*} \frac{\det D_\varrho}{\det Q} \! \sum_{n \le (N/d)^{1+{\epsilon}}} \! \frac{r(\textrm{gen}\ S_\varrho,n)^2}{n^{\frac{m}{2}-1}} \ll \frac{d^m}{N^m \det D_\varrho } \! \sum_{n \le (N/d)^{1+{\epsilon}}} \! n^{\frac{m}{2}-1} (n,N) \ll \Big(\frac{N}{d}\Big)^{-\frac{m}{2}} N^{{\epsilon}}.\end{align*}
As a result, the contribution of
![]() $r(\textrm{gen}\ S_\varrho,n)$
is bounded by
$r(\textrm{gen}\ S_\varrho,n)$
is bounded by
![]() $\mathcal{O}(N^{{\epsilon}})$
.
$\mathcal{O}(N^{{\epsilon}})$
.
For
![]() $Q = \textrm{diag}(a_1,\ldots,a_n)$
, the diagonal entries of
$Q = \textrm{diag}(a_1,\ldots,a_n)$
, the diagonal entries of
![]() $S_\varrho$
are given by
$S_\varrho$
are given by
We sort these entries by value and denote them by
![]() $a'_1,\ldots,a'_m$
. For
$a'_1,\ldots,a'_m$
. For
![]() $3 \le l_1,l_2 \le m+1$
, we estimate
$3 \le l_1,l_2 \le m+1$
, we estimate
 \begin{align*}\sqrt{a'_1 a'_2} \prod_{i=l_1}^m \sqrt{a'_i} \prod_{j=l_2}^m \sqrt{a'_j} \le\Big(\frac{N}{d}\Big)^{\frac{2m+4-l_1-l_2}{2}} \frac{\det D_\varrho}{\sqrt{a_m a_{m-1}}}. \end{align*}
\begin{align*}\sqrt{a'_1 a'_2} \prod_{i=l_1}^m \sqrt{a'_i} \prod_{j=l_2}^m \sqrt{a'_j} \le\Big(\frac{N}{d}\Big)^{\frac{2m+4-l_1-l_2}{2}} \frac{\det D_\varrho}{\sqrt{a_m a_{m-1}}}. \end{align*}
Thus, we get
 \begin{align*}\sum_{d \mid N} \Big(\frac{N}{d}\Big)^{\frac{m}{2}}\frac{\det D_\varrho}{\det Q} \sum_{n \le (N/d)^{1+{\epsilon}}} \frac{r(S_\varrho,n)^2}{n^{\frac{m}{2}-1}} \ll \left( \frac{N^{\frac{m}{2}}}{\det Q} \sum_{d \mid N} \frac{\det D_\varrho}{d^{\frac{m}{2}}} + \frac{N}{\sqrt{a_m a_{m-1}}} \right) N^{\epsilon}.\end{align*}
\begin{align*}\sum_{d \mid N} \Big(\frac{N}{d}\Big)^{\frac{m}{2}}\frac{\det D_\varrho}{\det Q} \sum_{n \le (N/d)^{1+{\epsilon}}} \frac{r(S_\varrho,n)^2}{n^{\frac{m}{2}-1}} \ll \left( \frac{N^{\frac{m}{2}}}{\det Q} \sum_{d \mid N} \frac{\det D_\varrho}{d^{\frac{m}{2}}} + \frac{N}{\sqrt{a_m a_{m-1}}} \right) N^{\epsilon}.\end{align*}
Applying (25) gives the second upper bound of Theorem 1.
It remains to determine a lower bound:
Proof of Theorem 3. By (23), we have that
 \begin{align} \langle \,f,f \rangle \geq \frac{\mu}{\tilde{\mu}} N \sum_{\substack{c\,(\textrm{mod}\ N) \\ d=(c,N)}} \sum_{\substack{a (\textrm{mod}\ N) \\ (a,d)=1}} \sum_{n=1}^\infty |a_{\varrho}(n)|^2 \int_{1}^{\infty} \textrm{exp}\left(\!- \frac{4 \pi y n d}{N}\right) y^{\frac{m}{2}-2} dy,\end{align}
\begin{align} \langle \,f,f \rangle \geq \frac{\mu}{\tilde{\mu}} N \sum_{\substack{c\,(\textrm{mod}\ N) \\ d=(c,N)}} \sum_{\substack{a (\textrm{mod}\ N) \\ (a,d)=1}} \sum_{n=1}^\infty |a_{\varrho}(n)|^2 \int_{1}^{\infty} \textrm{exp}\left(\!- \frac{4 \pi y n d}{N}\right) y^{\frac{m}{2}-2} dy,\end{align}
where
![]() $\varrho= (\begin{smallmatrix}a & * \\ c & *\end{smallmatrix})$
. For
$\varrho= (\begin{smallmatrix}a & * \\ c & *\end{smallmatrix})$
. For
![]() $t>0$
, it holds by substitution and [13, 2·33·5] that
$t>0$
, it holds by substitution and [13, 2·33·5] that
We drop all terms with
![]() $(c,N) > 1$
. For the remaining c and a, we have by Lemma 12 that
$(c,N) > 1$
. For the remaining c and a, we have by Lemma 12 that
![]() $|a_\varrho(n)|^2 = (\det Q)^{-1} |r(NQ^{-1},n) - r(\textrm{gen}\ NQ^{-1},n)|^2$
. Since
$|a_\varrho(n)|^2 = (\det Q)^{-1} |r(NQ^{-1},n) - r(\textrm{gen}\ NQ^{-1},n)|^2$
. Since
![]() $\frac{\mu}{\tilde{\mu}} N \varphi(N) = 1$
it follows that
$\frac{\mu}{\tilde{\mu}} N \varphi(N) = 1$
it follows that
 \begin{align*}\langle \,f,f \rangle \gg \frac{N^{\frac{m}{2}}}{\det Q} \sum_{n=1}^\infty \frac{r(NQ^{-1},n)^2}{n^{\frac{m}{2}-1}} e^{- \frac{4 \pi n}{N}} - \frac{N^{\frac{m}{2}}}{\det Q}\sum_{n=1}^\infty \frac{r(\textrm{gen }NQ^{-1},n)^2}{n^{\frac{m}{2}-1}} e^{- \frac{4 \pi n}{N}}.\end{align*}
\begin{align*}\langle \,f,f \rangle \gg \frac{N^{\frac{m}{2}}}{\det Q} \sum_{n=1}^\infty \frac{r(NQ^{-1},n)^2}{n^{\frac{m}{2}-1}} e^{- \frac{4 \pi n}{N}} - \frac{N^{\frac{m}{2}}}{\det Q}\sum_{n=1}^\infty \frac{r(\textrm{gen }NQ^{-1},n)^2}{n^{\frac{m}{2}-1}} e^{- \frac{4 \pi n}{N}}.\end{align*}
By (14) the latter term is bounded by
![]() $\mathcal{O}(N^{\epsilon})$
. For the former term, we apply Hermite’s theorem. This gives
$\mathcal{O}(N^{\epsilon})$
. For the former term, we apply Hermite’s theorem. This gives
As a result, we obtain
 \begin{align*} \sum_{n=1}^\infty \frac{r(NQ^{-1},n)^2}{n^{\frac{m}{2}-1}} \exp\Big(\!- \frac{ 2 \pi n}{N}\Big) \gg (\min N Q^{-1})^{1-\frac{m}{2}}. \end{align*}
\begin{align*} \sum_{n=1}^\infty \frac{r(NQ^{-1},n)^2}{n^{\frac{m}{2}-1}} \exp\Big(\!- \frac{ 2 \pi n}{N}\Big) \gg (\min N Q^{-1})^{1-\frac{m}{2}}. \end{align*}
This yields the claim.
4. Estimates for the error term
We start by deriving uniform estimates for the ternary case:
Lemma 13. Consider a positive, integral, ternary quadratic form
![]() $q(x) = x^T Q x/2$
. Then,
$q(x) = x^T Q x/2$
. Then,
 \begin{align*}|r(Q,n) - r(\mathrm{spn}\ Q,n)| \ll \frac{\sqrt{N}}{(\det Q)^\frac{1}{6}} \left(\frac{n^\frac{13}{28}}{N^{\frac{1}{7}}} + \frac{n^\frac{7}{16}}{N^{\frac{1}{16}}} + n^\frac{1}{4} \frac{\sqrt{(\tilde{n},N^\infty)} v^{\frac{1}{4}} \sqrt{(n,N)}}{\sqrt{N} }\right) (nN)^{\epsilon},\end{align*}
\begin{align*}|r(Q,n) - r(\mathrm{spn}\ Q,n)| \ll \frac{\sqrt{N}}{(\det Q)^\frac{1}{6}} \left(\frac{n^\frac{13}{28}}{N^{\frac{1}{7}}} + \frac{n^\frac{7}{16}}{N^{\frac{1}{16}}} + n^\frac{1}{4} \frac{\sqrt{(\tilde{n},N^\infty)} v^{\frac{1}{4}} \sqrt{(n,N)}}{\sqrt{N} }\right) (nN)^{\epsilon},\end{align*}
where
![]() $\tilde{n}$
is the largest divisor of n such that
$\tilde{n}$
is the largest divisor of n such that
![]() $(\tilde{n},N^\infty)$
is squarefree and
$(\tilde{n},N^\infty)$
is squarefree and
Proof. By a local argument of Blomer [Reference Blomer2, section 1·3], it is possible to write
for
![]() $Q_j, Q'_j$
in the same spinor genus and of level dividing N,
$Q_j, Q'_j$
in the same spinor genus and of level dividing N,
![]() $\sum_j |\gamma_j| \ll (nN)^{\epsilon}$
,
$\sum_j |\gamma_j| \ll (nN)^{\epsilon}$
,
![]() $m_j v_j w_j\mid n$
for all j,
$m_j v_j w_j\mid n$
for all j,
![]() $(m_j,N)=1$
,
$(m_j,N)=1$
,
![]() $w_j$
squarefree,
$w_j$
squarefree,
![]() $v_j \mid N^2$
and q anisotropic over all prime divisors of
$v_j \mid N^2$
and q anisotropic over all prime divisors of
![]() $v_j$
. The claim now follows by applying Theorem 1 and (8).
$v_j$
. The claim now follows by applying Theorem 1 and (8).
For
![]() $m \geq 4$
, we determine an effective lower bound for n with respect to Q. To this end, recall the definition of F(Q, s) given in (6).
$m \geq 4$
, we determine an effective lower bound for n with respect to Q. To this end, recall the definition of F(Q, s) given in (6).
Lemma 14. Let Q correspond to a positive, integral, quadratic form in m variables. Then, we have for
![]() $m=4$
that
$m=4$
that
 \begin{align*} |r(Q,n) - r(\mathrm{gen}\ Q,n)| &\ll n^{\frac{m}{4}-\frac{1}{2}} \left(\frac{N}{\sqrt{F(Q,2)}} + \frac{\sqrt{N}}{(\det Q)^\frac{1}{8}}\right) \\ &\times \min \left(\sqrt{N}, 1 + \frac{n^\frac{1}{4} (n,N)^\frac{1}{4} }{\sqrt{N}}\right) (nN)^{\epsilon}.\end{align*}
\begin{align*} |r(Q,n) - r(\mathrm{gen}\ Q,n)| &\ll n^{\frac{m}{4}-\frac{1}{2}} \left(\frac{N}{\sqrt{F(Q,2)}} + \frac{\sqrt{N}}{(\det Q)^\frac{1}{8}}\right) \\ &\times \min \left(\sqrt{N}, 1 + \frac{n^\frac{1}{4} (n,N)^\frac{1}{4} }{\sqrt{N}}\right) (nN)^{\epsilon}.\end{align*}
Let
![]() $\prod_p \beta_p(q,n) \gg \beta^{-1} (nN)^{-{\epsilon}}$
. Then,
$\prod_p \beta_p(q,n) \gg \beta^{-1} (nN)^{-{\epsilon}}$
. Then,
![]() $r(Q,n) \geq 1$
holds if
$r(Q,n) \geq 1$
holds if
For
![]() $m \geq 5$
, we have
$m \geq 5$
, we have
![]() $r(Q,n) \geq 1$
if
$r(Q,n) \geq 1$
if
 \begin{align*}n \gg \left( \beta^2 \sqrt{(n,N)} \left(N^{\frac{m}{2}-1} \frac{\det Q}{F\left(Q,\frac{m-1}{2}-\frac{1}{m}\right)} + (\det Q)^{1-\frac{2}{m}} \right) \right)^{\frac{2}{m-3}}.\end{align*}
\begin{align*}n \gg \left( \beta^2 \sqrt{(n,N)} \left(N^{\frac{m}{2}-1} \frac{\det Q}{F\left(Q,\frac{m-1}{2}-\frac{1}{m}\right)} + (\det Q)^{1-\frac{2}{m}} \right) \right)^{\frac{2}{m-3}}.\end{align*}
Moreover, we have that
 \begin{align*}\beta \leq \begin{cases}\sqrt{(n,N)} & \text{if } m=4 \text{ and } n \text{ primitively locally represented}, \\ \\[-7pt] \min( (n,N), (n,(\det Q)^{\frac{1}{m-4}})) & \text{if } m\geq 5 \text{ and } n \text{ locally represented}.\end{cases}\end{align*}
\begin{align*}\beta \leq \begin{cases}\sqrt{(n,N)} & \text{if } m=4 \text{ and } n \text{ primitively locally represented}, \\ \\[-7pt] \min( (n,N), (n,(\det Q)^{\frac{1}{m-4}})) & \text{if } m\geq 5 \text{ and } n \text{ locally represented}.\end{cases}\end{align*}
Proof. We apply (3) to bound the Fourier coefficients of
![]() $f(z) =\theta(Q,z)- \theta(\textrm{gen}\ Q,z)$
. For even m this is a result from [Reference Iwaniec and Kowalski18, corollary 14·24]. Since the Weil bound also holds for Kloosterman sums twisted by a quadratic character, cf. [Reference Waibel30, lemma 4], this result can be extended to odd m. In addition, we have for even m that
$f(z) =\theta(Q,z)- \theta(\textrm{gen}\ Q,z)$
. For even m this is a result from [Reference Iwaniec and Kowalski18, corollary 14·24]. Since the Weil bound also holds for Kloosterman sums twisted by a quadratic character, cf. [Reference Waibel30, lemma 4], this result can be extended to odd m. In addition, we have for even m that
by applying Deligne’s bound, cf. [Reference Schulze–Pillot and Yenirce26, theorem 11].
For
![]() $m=4$
, this result implies a substantial saving compared to previous lower bounds such as [Reference Rouse23, theorem 1]. For example if
$m=4$
, this result implies a substantial saving compared to previous lower bounds such as [Reference Rouse23, theorem 1]. For example if
![]() $(n,N) =1$
and
$(n,N) =1$
and
![]() $\det Q = F(Q,2)$
, a lower bound is given by
$\det Q = F(Q,2)$
, a lower bound is given by
![]() $n \gg (N^2 + (\det Q)^{4/3})N^{\epsilon}$
. For
$n \gg (N^2 + (\det Q)^{4/3})N^{\epsilon}$
. For
![]() $m=6$
, we obtain
$m=6$
, we obtain
which improves the lower bound
![]() $n \gg (\det Q)^{\frac{12}{5}}$
of Hsia and Icaza [Reference Hsia and Icaza16].
$n \gg (\det Q)^{\frac{12}{5}}$
of Hsia and Icaza [Reference Hsia and Icaza16].
5. Applications
We start with the problem of representing an integer by three squares of almost primes. To this end, we want to sieve the sequence
where
![]() $n \equiv 3\,(\textrm{mod}\ 24)$
,
$n \equiv 3\,(\textrm{mod}\ 24)$
,
![]() $5 \nmid n$
. Let d denote a squarefree integer and
$5 \nmid n$
. Let d denote a squarefree integer and
![]() $\mathcal{A}_d$
the subset of all
$\mathcal{A}_d$
the subset of all
![]() $a \in \mathcal{A}$
that are divisible by d. Moreover, let
$a \in \mathcal{A}$
that are divisible by d. Moreover, let
![]() $\textbf{l} = (l_1,l_2,l_3)$
,
$\textbf{l} = (l_1,l_2,l_3)$
,
![]() $\mu(\textbf{l}) = \mu(l_1) \mu(l_2) \mu(l_3)$
and
$\mu(\textbf{l}) = \mu(l_1) \mu(l_2) \mu(l_3)$
and
![]() $q_\textbf{l}(x) = l_1^2 x_1^2 + l_2^2 x_2^2 + l_3^2 x_3^2$
with corresponding matrix
$q_\textbf{l}(x) = l_1^2 x_1^2 + l_2^2 x_2^2 + l_3^2 x_3^2$
with corresponding matrix
![]() $Q_\textbf{l}$
. An application of the inclusion-exclusion principle gives
$Q_\textbf{l}$
. An application of the inclusion-exclusion principle gives
We decompose
![]() $r(Q_\textbf{l},n) = r(\textrm{gen}\ Q_\textbf{l},n) + a(n)$
. For the main term, we have
$r(Q_\textbf{l},n) = r(\textrm{gen}\ Q_\textbf{l},n) + a(n)$
. For the main term, we have
 \begin{equation*}r(\textrm{gen}\ Q_\textbf{l},n) = \frac{\pi n^\frac{1}{2}}{4 l_1 l_2 l_3} \prod_p \beta_p(Q_\textbf{l},n).\end{equation*}
\begin{equation*}r(\textrm{gen}\ Q_\textbf{l},n) = \frac{\pi n^\frac{1}{2}}{4 l_1 l_2 l_3} \prod_p \beta_p(Q_\textbf{l},n).\end{equation*}
For
![]() $\textbf{1}=(1,1,1)$
, we have
$\textbf{1}=(1,1,1)$
, we have
![]() $\beta_p(Q_\textbf{1},n) \gg n^{-{\epsilon}}$
for
$\beta_p(Q_\textbf{1},n) \gg n^{-{\epsilon}}$
for
![]() $n \equiv 3\, (\textrm{mod}\ 8)$
. Hence, we may set
$n \equiv 3\, (\textrm{mod}\ 8)$
. Hence, we may set
and
 \begin{equation*} \frac{\Omega(d)}{d} = \prod_{p \mid d} \frac{\Omega(p)}{p} \,{:\!=}\, \mu(d) \sum_{\substack{l \in {\mathbb N}^3, [l_1,l_2,l_3]=d}} \mu(l_1) \mu(l_2) \mu(l_3) \frac{\omega(\textbf{l},n)}{l_1 l_2 l_3}.\end{equation*}
\begin{equation*} \frac{\Omega(d)}{d} = \prod_{p \mid d} \frac{\Omega(p)}{p} \,{:\!=}\, \mu(d) \sum_{\substack{l \in {\mathbb N}^3, [l_1,l_2,l_3]=d}} \mu(l_1) \mu(l_2) \mu(l_3) \frac{\omega(\textbf{l},n)}{l_1 l_2 l_3}.\end{equation*}
The functions
![]() $\omega(\textbf{l},n)$
are explicitly computed in [Reference Blomer and Brüdern3, lemma 3·1 and 3·2]. This yields for
$\omega(\textbf{l},n)$
are explicitly computed in [Reference Blomer and Brüdern3, lemma 3·1 and 3·2]. This yields for
![]() $n \equiv 3 \,(\textrm{mod}\ 24)$
,
$n \equiv 3 \,(\textrm{mod}\ 24)$
,
![]() $5 \nmid n$
that
$5 \nmid n$
that
![]() $0 \leq \Omega(p) <p$
. Furthermore, there is constant
$0 \leq \Omega(p) <p$
. Furthermore, there is constant
![]() $A \ge 2$
such that
$A \ge 2$
such that
 \begin{align*}\prod_{z_1 \le p < z} \left(1- \frac{\Omega(p)}{p} \right)^{-1} \le \left(\frac{\log z}{\log z_1}\right)^3 \left(1+ \frac{A}{{\log z_1}}\right) \text{ for } 2 \le z_1 \le z.\end{align*}
\begin{align*}\prod_{z_1 \le p < z} \left(1- \frac{\Omega(p)}{p} \right)^{-1} \le \left(\frac{\log z}{\log z_1}\right)^3 \left(1+ \frac{A}{{\log z_1}}\right) \text{ for } 2 \le z_1 \le z.\end{align*}
For
![]() $X \,{:\!=}\, \frac{\pi}{4} n^\frac{1}{2} \prod_p \beta_p(Q_\textbf{1},n)$
, we obtain that
$X \,{:\!=}\, \frac{\pi}{4} n^\frac{1}{2} \prod_p \beta_p(Q_\textbf{1},n)$
, we obtain that
![]() $|\mathcal{A}_d| = \frac{\Omega(d)}{d} X + R_d(\mathcal{A})$
, where
$|\mathcal{A}_d| = \frac{\Omega(d)}{d} X + R_d(\mathcal{A})$
, where
Let
![]() $F_3(s)$
and
$F_3(s)$
and
![]() $f_3(s)$
denote the three dimensional sieve functions given in [Reference Diamond and Halberstam10, theorem 1]. Then, it holds by [Reference Diamond and Halberstam10, theorem 1] for
$f_3(s)$
denote the three dimensional sieve functions given in [Reference Diamond and Halberstam10, theorem 1]. Then, it holds by [Reference Diamond and Halberstam10, theorem 1] for
![]() $\kappa =3$
that:
$\kappa =3$
that:
Lemma 15. Let
![]() $\mathcal{A}, X, \Omega$
as above and write v(d) for the number of prime factors of d. Furthermore, let
$\mathcal{A}, X, \Omega$
as above and write v(d) for the number of prime factors of d. Furthermore, let
for
![]() $\tau \in {\mathbb R}$
with
$\tau \in {\mathbb R}$
with
![]() $0< \tau <1$
. Then, it holds for any
$0< \tau <1$
. Then, it holds for any
![]() $u,v \in {\mathbb R}$
with
$u,v \in {\mathbb R}$
with
![]() $1/\tau <u <v$
and
$1/\tau <u <v$
and
![]() $\tau v > \beta_3 \,{:\!=}\, 6.6408$
that
$\tau v > \beta_3 \,{:\!=}\, 6.6408$
that
 \begin{align*}|\{P_r \mid P_r \in \mathcal{A}\}| \gg X \prod_{p < X^\frac{1}{v}} \Big(1 - \frac{\Omega(p)}{p}\Big)\end{align*}
\begin{align*}|\{P_r \mid P_r \in \mathcal{A}\}| \gg X \prod_{p < X^\frac{1}{v}} \Big(1 - \frac{\Omega(p)}{p}\Big)\end{align*}
provided only that
We prove the following improvement of [Reference Lü20, lemma 4·1]:
Lemma 16. Let
![]() $n \equiv 3\, (\mathrm{mod}\ 24), 5 \nmid n$
and
$n \equiv 3\, (\mathrm{mod}\ 24), 5 \nmid n$
and
![]() $\tau < {3}/{58}$
. Then,
$\tau < {3}/{58}$
. Then,
 \begin{align*}\sum_{d \leq n^\frac{\tau}{2}} \mu^2(d) 4^{v(d)} |R_d(\mathcal{A})| \ll n^{\frac{1}{2}-{\epsilon}}.\end{align*}
\begin{align*}\sum_{d \leq n^\frac{\tau}{2}} \mu^2(d) 4^{v(d)} |R_d(\mathcal{A})| \ll n^{\frac{1}{2}-{\epsilon}}.\end{align*}
Proof. We only consider combinations of
![]() $l_1,l_2,l_3$
such that either
$l_1,l_2,l_3$
such that either
![]() $r(Q_\textbf{l},n) \neq 0$
or
$r(Q_\textbf{l},n) \neq 0$
or
![]() $r(\textrm{gen}\ Q_\textbf{l},n) \neq 0$
. The remaining forms are isotropic over all odd primes and satisfy
$r(\textrm{gen}\ Q_\textbf{l},n) \neq 0$
. The remaining forms are isotropic over all odd primes and satisfy
![]() $2 \nmid l_1l_2l_3$
. It follows by (9) that
$2 \nmid l_1l_2l_3$
. It follows by (9) that
![]() $r(\textrm{gen}\ Q_\textbf{l},n) = r(\textrm{spn}\ Q_\textbf{l},n)$
. Since the level of
$r(\textrm{gen}\ Q_\textbf{l},n) = r(\textrm{spn}\ Q_\textbf{l},n)$
. Since the level of
![]() $Q_\textbf{l}$
is given by 4d we infer by Lemma 13 that
$Q_\textbf{l}$
is given by 4d we infer by Lemma 13 that
 \begin{align*}&\sum_{d \leq n^{\tau/2}} \mu^2(d) \sum_{ [l_1,l_2,l_3]=d} \mu^2(\textbf{l}) 4^{v(d)} |r(Q_\textbf{l},n) - r(\textrm{gen}\ Q_\textbf{l},n)| \\[4pt] &\ll \sum_{d \leq n^{\tau/2}} d^{\frac{2}{3}} \left( \frac{n^{\frac{13}{28}}}{d^{\frac{2}{7}}} + \frac{n^{\frac{7}{16}}}{d^{\frac{1}{8}}} + n^{\frac{1}{4}} \frac{\sqrt{(n,d)(n,d^2)}}{d} \right) d^{\epsilon},\end{align*}
\begin{align*}&\sum_{d \leq n^{\tau/2}} \mu^2(d) \sum_{ [l_1,l_2,l_3]=d} \mu^2(\textbf{l}) 4^{v(d)} |r(Q_\textbf{l},n) - r(\textrm{gen}\ Q_\textbf{l},n)| \\[4pt] &\ll \sum_{d \leq n^{\tau/2}} d^{\frac{2}{3}} \left( \frac{n^{\frac{13}{28}}}{d^{\frac{2}{7}}} + \frac{n^{\frac{7}{16}}}{d^{\frac{1}{8}}} + n^{\frac{1}{4}} \frac{\sqrt{(n,d)(n,d^2)}}{d} \right) d^{\epsilon},\end{align*}
where we estimated
![]() $\#\{ \textbf{l} \in {\mathbb N}^3 \mid [l_1,l_2,l_3] =d\} \le \tau(d)^3 \ll d^{\epsilon}$
in the second step. For
$\#\{ \textbf{l} \in {\mathbb N}^3 \mid [l_1,l_2,l_3] =d\} \le \tau(d)^3 \ll d^{\epsilon}$
in the second step. For
![]() $\tau < {3}/{58}$
the display above is bounded by
$\tau < {3}/{58}$
the display above is bounded by
![]() $\ll n^{\frac{1}{2}-{\epsilon}}$
.
$\ll n^{\frac{1}{2}-{\epsilon}}$
.
To avoid the computation of
![]() $F_3(s)$
and
$F_3(s)$
and
![]() $f_3(s)$
, we apply a well known trick. If we set
$f_3(s)$
, we apply a well known trick. If we set
![]() $\tau u = 1 + \zeta - \zeta/ \beta_3$
and
$\tau u = 1 + \zeta - \zeta/ \beta_3$
and
![]() $\tau v = \beta_3 / \zeta + \beta_k -1$
, it follows by (10·1·10), (10·2·4) and (10·2·7) in [Reference Halberstam and Richert14] that
$\tau v = \beta_3 / \zeta + \beta_k -1$
, it follows by (10·1·10), (10·2·4) and (10·2·7) in [Reference Halberstam and Richert14] that
This gives the following slightly weaker version of (27):
For
![]() $\tau = 3/58$
it follows that
$\tau = 3/58$
it follows that
This proves Corollary 4.
Even for four squares of primes, current technology is not sufficient to prove that every
![]() $n \equiv 4\,(\textrm{mod}\ 24)$
is represented. By means of sieving and Theorem 1, we can address this problem for almost primes. Here, the main input is:
$n \equiv 4\,(\textrm{mod}\ 24)$
is represented. By means of sieving and Theorem 1, we can address this problem for almost primes. Here, the main input is:
Lemma 17. Let
![]() $n \equiv 4\, (\mathrm{mod}\ 24)$
,
$n \equiv 4\, (\mathrm{mod}\ 24)$
,
![]() $\tau < {1}/{2}$
,
$\tau < {1}/{2}$
,
![]() $q_\textbf{l}(x) = l_1^2 x_1^2 + l_2^2x_2^2+l_3^2 x_3^2 + x_4^2 l_4^2$
. Then,
$q_\textbf{l}(x) = l_1^2 x_1^2 + l_2^2x_2^2+l_3^2 x_3^2 + x_4^2 l_4^2$
. Then,
 \begin{align*} \sum_{d \leq n^\frac{\tau}{2}} \mu(d) \sum_{\substack{ l \in {\mathbb N}^4 \\ d=[l_1,l_2,l_3,l_4]}} \mu(\textbf{l}) 4^{v(d)} |r(Q_\textbf{l},n) - r(\mathrm{gen}\ Q_\textbf{l},d)| \ll n^{\frac{1}{2}-{\epsilon}}. \end{align*}
\begin{align*} \sum_{d \leq n^\frac{\tau}{2}} \mu(d) \sum_{\substack{ l \in {\mathbb N}^4 \\ d=[l_1,l_2,l_3,l_4]}} \mu(\textbf{l}) 4^{v(d)} |r(Q_\textbf{l},n) - r(\mathrm{gen}\ Q_\textbf{l},d)| \ll n^{\frac{1}{2}-{\epsilon}}. \end{align*}
By applying the weighted four dimensional sieve from [Reference Diamond and Halberstam10] it follows that every
![]() $n\equiv 4\, (\textrm{mod}\ 24)$
is represented by
$n\equiv 4\, (\textrm{mod}\ 24)$
is represented by
![]() $x_1^2 + x_2^2 + x_3^2 + x_4^2$
with
$x_1^2 + x_2^2 + x_3^2 + x_4^2$
with
![]() $x_1 x_2 x_3 x_4 \in P_{20}$
. However, a recent approach by Tsang, Zhao [Reference Tsang and Zhao29] and Ching [Reference Ching9] yields much better results. Their idea is to choose one of the
$x_1 x_2 x_3 x_4 \in P_{20}$
. However, a recent approach by Tsang, Zhao [Reference Tsang and Zhao29] and Ching [Reference Ching9] yields much better results. Their idea is to choose one of the
![]() $x_i$
’s as a prime and then to combine Chen’s switching result with a three dimensional sieve. This shows that
$x_i$
’s as a prime and then to combine Chen’s switching result with a three dimensional sieve. This shows that
![]() $n = p^2 + x_1^2 + x_2^2 + x_3^2$
for a prime p and
$n = p^2 + x_1^2 + x_2^2 + x_3^2$
for a prime p and
![]() $x_1x_2x_3 \in P_{12}$
.
$x_1x_2x_3 \in P_{12}$
.
To tackle the problem of representing an integer by three squares of smooth numbers, we follow the approach in [Reference Blomer, Brüdern and Dietmann4]. The underlying idea is to choose integers
![]() $d_1,d_2,d_3 \in [n^{\eta}, 2 n^{\eta}]$
with
$d_1,d_2,d_3 \in [n^{\eta}, 2 n^{\eta}]$
with
![]() $\eta$
as large as possible such that
$\eta$
as large as possible such that
is soluble. To obtain a lower bound for
![]() $r(\textrm{spn}\ Q,n)$
, we choose
$r(\textrm{spn}\ Q,n)$
, we choose
![]() $d_1,d_2,d_3$
to be distinct primes that are
$d_1,d_2,d_3$
to be distinct primes that are
![]() $\equiv 1 \,(\textrm{mod}\ 4)$
and coprime to n. This implies that
$\equiv 1 \,(\textrm{mod}\ 4)$
and coprime to n. This implies that
Furthermore, we obtain by Lemma 13 that
 \begin{align} | r(Q,n) - r(\textrm{spn}\ Q,n)| &\ll (d_1d_2d_3)^\frac{2}{3} \left(\frac{n^{\frac{13}{28}}}{(d_1d_2d_3)^{2/7}} + \frac{n^{\frac{7}{16}}}{(d_1d_2d_3)^{1/8}} \right) n^{\epsilon} \end{align}
\begin{align} | r(Q,n) - r(\textrm{spn}\ Q,n)| &\ll (d_1d_2d_3)^\frac{2}{3} \left(\frac{n^{\frac{13}{28}}}{(d_1d_2d_3)^{2/7}} + \frac{n^{\frac{7}{16}}}{(d_1d_2d_3)^{1/8}} \right) n^{\epsilon} \end{align}
Hence, for
![]() $\eta = {1}/{116}-{\epsilon}$
, equation (29) is dominated by (28) and it follows that
$\eta = {1}/{116}-{\epsilon}$
, equation (29) is dominated by (28) and it follows that
![]() $r(Q,n) \geq 1$
for n sufficiently large. This proves the first claim of Corollary 5.
$r(Q,n) \geq 1$
for n sufficiently large. This proves the first claim of Corollary 5.
To derive results for sums of four squares, we make use of the distribution of smooth numbers in short intervals. For every
![]() $n \in {\mathbb N}$
it is possible to choose x with largest prime factor not exceeding
$n \in {\mathbb N}$
it is possible to choose x with largest prime factor not exceeding
![]() $n^\frac{1}{4}$
such that
$n^\frac{1}{4}$
such that
![]() $0 \leq n -x^2 \leq n^\frac{5}{8}$
and
$0 \leq n -x^2 \leq n^\frac{5}{8}$
and
![]() ${n -x^2 \not\equiv 0,1,4,7\,(\textrm{mod}\ 8)}$
, see [Reference Blomer, Brüdern and Dietmann4, section 5] for details. By our previous result for three squares, this implies that every sufficiently large n is represented by the sum of four squares whose largest prime divisors do not exceed
${n -x^2 \not\equiv 0,1,4,7\,(\textrm{mod}\ 8)}$
, see [Reference Blomer, Brüdern and Dietmann4, section 5] for details. By our previous result for three squares, this implies that every sufficiently large n is represented by the sum of four squares whose largest prime divisors do not exceed
![]() $n^\frac{\theta}{2}$
where
$n^\frac{\theta}{2}$
where
![]() $\theta = {285}/{464}$
.
$\theta = {285}/{464}$
.
The bounds for three smooth squares can be improved, if we choose
![]() $d_1 = e_1 e_2$
,
$d_1 = e_1 e_2$
,
![]() ${d_2 = e_1 e_3}$
and
${d_2 = e_1 e_3}$
and
![]() $d_3 = e_2 e_3$
for
$d_3 = e_2 e_3$
for
![]() $e_1,e_2,e_3$
mutually coprime and
$e_1,e_2,e_3$
mutually coprime and
![]() $(e_1e_2e_3,n)=1$
. However, this only works, if
$(e_1e_2e_3,n)=1$
. However, this only works, if
![]() $\big({p}/{n} \big) =1$
for every prime divisor p of
$\big({p}/{n} \big) =1$
for every prime divisor p of
![]() $e_1 e_2 e_3$
, since then
$e_1 e_2 e_3$
, since then
![]() $\beta_p(n,Q) = 1 + \big({p}/{n} \big) =2$
. If this latter condition is satisfied, we can choose
$\beta_p(n,Q) = 1 + \big({p}/{n} \big) =2$
. If this latter condition is satisfied, we can choose
![]() $\eta = {1}/{80}- {\epsilon}$
.
$\eta = {1}/{80}- {\epsilon}$
.