Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-07T00:41:14.906Z Has data issue: false hasContentIssue false
  • English
  • Français

On the essential spectrum of phase-space anisotropic pseudodifferential operators

Published online by Cambridge University Press:  02 July 2012

MARIUS MĂNTOIU
MARIUS MĂNTOIU*
Affiliation:
Departamento de Matemáticas, Facultad de Ciencias, Universidad de Chile, Las Palmeras 3425, Casilla 653, Santiago, Chile e-mail: mantoiu@uchile.cl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A phase-space anisotropic operator in 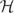=L2(ℝn) is a self-adjoint operator whose resolvent family belongs to a natural C*-completion of the space of Hörmander symbols of order zero. Equivalently, each member of the resolvent family is norm-continuous under conjugation with the Schrödinger unitary representation of the Heisenberg group. The essential spectrum of such a phase-space anisotropic operator is the closure of the union of usual spectra of all its “phase-space asymptotic localizations”, obtained as limits over diverging ultrafilters of ℝn×ℝn-translations of the operator. The result extends previous analysis of the purely configurational anisotropic operators, for which only the behavior at infinity in ℝn was allowed to be non-trivial.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 154 , Issue 1 , January 2013 , pp. 29 - 39
Copyright
Copyright © Cambridge Philosophical Society 2012

References

REFERENCES

[1]Amrein, W. O., Boutet de Monvel, A. and Georgescu, V.C 0-Groups, Commutator Methods and Spectral Theory of N-Body Hamiltonians (Birkhäuser, Basel, 1996).Google Scholar
[2]Beltiţă, I. and Măntoiu, M. Rieffel quantization and twisted crossed products. submitted.Google Scholar
[3]Bourbaki, N.Eléments de Mathématique: Topologie générale (Hermann, Paris, 1971). Ch. 14Google Scholar
[4]Davies, E. B.Heat Kernels and Spectral Theory (Cambridge University Press, 1989).CrossRefGoogle Scholar
[5]Davies, E. B.Decomposing the essential spectrum. J. Funct. Anal. 257 no. 2, (2009), 506–536.CrossRefGoogle Scholar
[6]Davies, E. B. and Georgescu, V.C*-algebras associated with some second order differential operators. Preprint ArXiV and to appear in J. Operator Theory.Google Scholar
[7]Folland, G. B.Harmonic Analysis in Phase Space. Ann. Math. Stud. 122 (Princeton University Press, Princeton, NJ, 1989).CrossRefGoogle Scholar
[8]Georgescu, V.On the structure of the essential spectrum of elliptic operators in metric spaces. J. Funct. Anal. 260 (2011), 1734–1765.CrossRefGoogle Scholar
[9]Georgescu, V. and Iftimovici, A.Crossed Products of C*-algebras and spectral analysis of quantum Hamiltonians. Commun. Math. Phys. 228 (2002), 519–560.CrossRefGoogle Scholar
[10]Georgescu, V. and Iftimovici, A.Riesz Kolmogorov compactness criterion, Lorentz convergence and Ruelle theorem on locally compact Abelian groups. Potential Analysis 20, (2004) 265–284.CrossRefGoogle Scholar
[11]Georgescu, V. and Iftimovici, A.Localizations at infinity and essential spectrum of quantum Hamiltonians. I. General Theory. Rev. Math. Phys. 18 (4), (2006), 417–483.CrossRefGoogle Scholar
[12]Helffer, B. and Mohamed, A.Caractérisation du spectre essentiel de l'opérateur de Schrödinger avec un champ magnétique. Ann. Inst. Fourier 38 no. 2 (1988), 95–112.CrossRefGoogle Scholar
[13]Kasprzak, P.Rieffel deformation via crossed products. J. Funct. Anal. 257 no. 5 (2009), 1228–1332.CrossRefGoogle Scholar
[14]Last, Y. and Simon, B.The essential spectrum of Schrödinger, Jacobi and CMV operators. J. d'Analyse Math. 98 (2006), 183–220.CrossRefGoogle Scholar
[15]Lauter, R. and Nistor, V.Analysis of geometric operators on open manifolds: a Groupoid Approach. In Quantization of Singular Symplectic Quotient. Progr. Math. 198 (Birkhäuser, Basel 2001), 181–229.CrossRefGoogle Scholar
[16]Măntoiu, M.Compactifications, dynamical systems at infinity and the essential spectrum of generalized Schödinger operators. J. Reine Angew. Math. 550 (2002), 211–229.Google Scholar
[17]Măntoiu, M. Rieffel's pseudodifferential calculus and spectral analysis for quantum Hamiltonians. Preprint ArXiV and to appear in Ann. Inst. Fourier.Google Scholar
[18]Măntoiu, M., Purice, R. and Richard, S.Spectral and propagation results for magnetic Schrödinger operators; a C*-algebraic framework. J. Funct. Anal. 250 (2007), 42–67.CrossRefGoogle Scholar
[19]Rieffel, M. A.Deformation quantization for actions of ℝd. Memoirs Amer. Math. Soc. 506 (1993).Google Scholar
[20]Rabinovich, V. S., Roch, S. and Roe, J.Fredholm indices of band-dominated operators. Int. Eq. Op. Th. 49 (2004), 221–238.Google Scholar
[21]Rabinovich, V. S., Roch, S. and Silbermann, B.Limit Operators and their Applications In Operator Theory. Operator Theory: Adv. and Applic. 150 (Birkhäuser, Basel, 2004).Google Scholar
[22]Raeburn, I. and Williams, D.Morita Equivalence and Continuous-Trace C*-Algebras. Math. Surv. Monogr. 60 (American Mathematical Society, 1998).CrossRefGoogle Scholar
[23]Röckner, M. and Wielens, N.Dirichlet Forms - Closability and Change of Speed Measure. In Infinite Dimensional Analysis and Stochastic Processes, Rese. Notes in Mathe. 124 (Pitman 1985), 119–144.Google Scholar
[24]Woronowicz, S. L.Unbounded elements affiliated with C*-algebras and non-compact quantum groups. Commun. Math. Phys. 136 (1991), 399–432.CrossRefGoogle Scholar