Hostname: page-component-6dbcb7884d-2bcm2 Total loading time: 0 Render date: 2025-02-14T08:13:16.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Moduli of wild Higgs bundles on 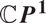$\mathbb{C}P^1$ with $\mathbb{C}^\times$-actions

Part of: Global differential geometry

Published online by Cambridge University Press:  03 June 2021

LAURA FREDRICKSON  and
ANDREW NEITZKE
LAURA FREDRICKSON
Affiliation:
Department of Mathematics, University of Oregon, Eugene, OR97403, U.S.A. e-mail: lfredric@uoregon.edu
ANDREW NEITZKE
Affiliation:
Department of Mathematics, Yale University, Attn: Andrew Neitzke, PO Box 208283, New Haven, CT06520-8283, U.S.A. e-mail: andrew.neitzke@yale.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a set 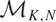$\mathcal{M}_{K,N}$ parameterising filtered SL(K)-Higgs bundles over 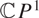$\mathbb{C}P^1$ with an irregular singularity at 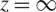$z = \infty$, such that the eigenvalues of the Higgs field grow like 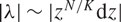$\vert \lambda \vert \sim \vert z^{N/K} \mathrm{d}z \vert$, where K and N are coprime. 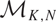$\mathcal{M}_{K,N}$ carries a 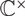$\mathbb{C}^\times$-action analogous to the famous 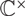$\mathbb{C}^\times$-action introduced by Hitchin on the moduli spaces of Higgs bundles over compact curves. The construction of this $\mathbb{C}^\times$-action on $\mathcal{M}_{K,N}$ involves the rotation automorphism of the base 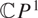$\mathbb{C}P^1$. We classify the fixed points of this $\mathbb{C}^\times$-action, and exhibit a curious 1-1 correspondence between these fixed points and certain representations of the vertex algebra $\mathcal{W}_K$ ; in particular we have the relation $\mu = {k-1-c_{\mathrm{eff}}}/{12}$ , where 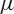$\mu$ is a regulated version of the L2 norm of the Higgs field, and 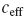$c_{\mathrm{eff}}$ is the effective Virasoro central charge of the corresponding W-algebra representation. We also discuss a Białynicki–Birula-type decomposition of $\mathcal{M}_{K,N}$ , where the strata are labeled by isomorphism classes of the underlying filtered vector bundles.

MSC classification

Primary: 53C07: Special connections and metrics on vector bundles (Hermite-Einstein-Yang-Mills)
Secondary: 53C56: Other complex differential geometry
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 3 , November 2021 , pp. 623 - 656
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arakawa, T., Creutzig, T. and Linshaw, A. R.. W-algebras as coset vertex algebras. Invent. Math., 218 (2019), no. 1:145–195.CrossRefGoogle Scholar
Beem, C., Lemos, M., Liendo, P., Peelaers, W., Rastelli, L. and van Rees, B.. Infinite chiral symmetry in four dimensions. Commun. Math. Phys. 336 (2015), no. 3:1359–1433.CrossRefGoogle Scholar
Białynicki-Birula, A.. Some theorems on actions of algebraic groups. Ann. of Math. (1973), 98:480–497.CrossRefGoogle Scholar
Biquard, O. and Boalch, P.. Wild nonabelian Hodge theory on curves. Compositio Math. (2004), 140:179–204.CrossRefGoogle Scholar
Boalch, P. and Yamakawa, D.. Twisted wild character varieties. arXiv:1512.08091 (2015).Google Scholar
Bouwknegt, P. and Schoutens, K.. W-symmetry in conformal field theory. Physics Reports 223 (1993), no. 4:183–276.CrossRefGoogle Scholar
Cecotti, S., Neitzke, A. and Vafa, C.. R-Twisting and 4d/2d correspondences. arXiv:1006.3435. (2010).Google Scholar
Cecotti, S. and Vafa, C.. Topological-antitopological fusion. Nucl. Phys. (1991), B367:359–461.CrossRefGoogle Scholar
Cherkis, S. A. and Kapustin, A.. Nahm transform for periodic monopoles and ${\cal N} = 2$ super Yang-Mills theory. Commun. Math. Phys. (2001), 218:333–371.CrossRefGoogle Scholar
Cherkis, S. A. and Kapustin, A.. Periodic monopoles with singularities and ${\cal N} = 2$ super-QCD. Commun. Math. Phys. (2003), 234:1–35.CrossRefGoogle Scholar
Córdova, C., Gaiotto, D. and Shao, S. H.. Infrared computations of defect Schur indices. JHEP (2016), 11:106.CrossRefGoogle Scholar
Córdova, C., Gaiotto, D. and Shao, S. H.. Surface defect indices and 2d-4d BPS states. JHEP (2017), 12:78.CrossRefGoogle Scholar
Córdova, C., Gaiotto, D. and Shao, S. H.. Surface defects and chiral algebras. JHEP (2017), 05:140.CrossRefGoogle Scholar
Córdova, C. and Shao, S. H.. Schur indices, BPS particles and Argyres–Douglas theories. JHEP (2016), 1:1–38.Google Scholar
Fateev, V. A. and Lukyanov, S. L.. The models of two-dimensional conformal quantum field theory with Z(n) symmetry. Int. J. Mod. Phys. (1988), A3:507.CrossRefGoogle Scholar
Fateev, V. A. and Zamolodchikov, A. B.. Conformal quantum field theory models in two-dimensions having Z(3) symmetry. Nucl. Phys. (1987), B280:644–660.CrossRefGoogle Scholar
Fredrickson, L., Pei, D., Yan, W. and Ye, K.. Argyres–Douglas theories, chiral algebras and wild Hitchin characters. JHEP 105 (2018).CrossRefGoogle Scholar
Gaiotto, D., Moore, G. W. and Neitzke, A.. Wall-crossing, Hitchin systems and the WKB approximation. Adv. Math (2013), 234:239–403.CrossRefGoogle Scholar
García-Prada, O., Gothen, P. and Muñoz, V.. Betti numbers of the moduli space of rank 3 parabolic Higgs bundles. Memoirs of the AMS, 187 (2007), no. 879.CrossRefGoogle Scholar
García-Prada, O., Heinloth, J. and Schmitt, A.. On the motives of moduli of chains and Higgs bundles. arXiv:1104.5558. (2011).Google Scholar
Gothen, P.. The Betti numbers of the moduli space of stable rank 3 Higgs bundles on a Riemann surface. International J. Math (1994), 5:861–875.CrossRefGoogle Scholar
Gothen, P. and Zuniga–Rojas, R.. Stratifications of the moduli space of Higgs bundles. Portugaliae Mathematica (2015), 74(2).Google Scholar
Hitchin, N.. The self-duality equations on a Riemann surface. Proc. London Math. Soc. (1987), 3(1):59–126.CrossRefGoogle Scholar
Hitchin, N.. Lie groups and Teichmüller space. Topology, 21(3) (1992), 449–473.CrossRefGoogle Scholar
Huybrechts, D.. Complex geometry . Universitext. (Springer-Verlag, Berlin, 2005).Google Scholar
Konno, H.. Construction of the moduli space of stable parabolic Higgs bundles on a Riemann surface. J. Math. Soc. Japan 45(2) (1993), 253–276.CrossRefGoogle Scholar
Mazzeo, R., Swoboda, J., Weiss, H. and Witt, F.. Ends of the moduli space of Higgs bundles. Duke Math. J., 165(12) (2016), 2227–2271.CrossRefGoogle Scholar
McCoy, B., Tracy, C. and Wu, T. T.. Arithmetic harmonic analysis on character and quiver varieties. J. of Mathematical Physics, 118(4):1058–1092, (21977).Google Scholar
Mochizuki, T.. Harmonic bundles and Toda lattices with opposite sign. arXiv:1301.1718 (2013).CrossRefGoogle Scholar
Neitzke, A.. Hitchin systems in ${\cal N} = 2$ field theory. 2014. In “Exact results in supersymmetric field theory,” edited by Teschner, J..CrossRefGoogle Scholar
Neitzke, A. and Yan, F.. Line defect Schur indices, Verlinde algebras and U(1) r fixed points. JHEP 1711 (2017), no. 35.Google Scholar
Piontkowski, J.. Topology of the compactified Jacobians of singular curves. Mathematische Zeitschrift, 255(1) (2007), 195–226.CrossRefGoogle Scholar
Simpson, C.. The Hodge filtration on nonabelian cohomology. In Algebraic geometry—Santa Cruz 1995, volume 62 of Proc. Sympos. Pure Math. Amer. Math. Soc. (Providence, RI, 1997), 217–281.CrossRefGoogle Scholar
Simpson, C. T.. Harmonic bundles on noncompact curves. Journal of the America Mathematical Society, 3(3) (1990), 713–770.CrossRefGoogle Scholar
Simpson, C. T.. Higgs bundles and local systems. Inst. Hautes Études Sci. Publ. Math. (75) (1992), 5–95.CrossRefGoogle Scholar
Song, J.. Superconformal indices of generalized Argyres–Douglas theories from 2d TQFT. JHEP, 13 (11) (2015).Google Scholar
Witten, E.. Solutions of four-dimensional field theories via M-theory. Nucl. Phys., B500:3–42, (1997).CrossRefGoogle Scholar
Xie, D.. General Argyres–Douglas theory. JHEP (100 no. 1 (2013)).CrossRefGoogle Scholar
Yokogawa, K.. Compactification of moduli of parabolic sheaves and moduli of parabolic Higgs sheaves. J. Math. Kyoto Univ., 33(2):451–504 (1993).Google Scholar