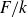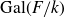1. Introduction
Let A be an abelian variety defined over a number field k. The Birch and Swinnerton–Dyer conjecture for A over k (as extended to this setting by Tate) predicts a remarkable equality between the leading term
![]() $L^*(A,1)$
at
$L^*(A,1)$
at
![]() $z=1$
of the Hasse–Weil L-series L(A,z) of A over k (assuming that this function has a suitable meromorphic continuation) and the key algebraic invariants of A over k.
$z=1$
of the Hasse–Weil L-series L(A,z) of A over k (assuming that this function has a suitable meromorphic continuation) and the key algebraic invariants of A over k.
Nevertheless, there are various natural contexts in which it seems likely that this equality does not encompass the full extent of the interplay between the leading terms
![]() $L^*(A,\psi,1)$
at
$L^*(A,\psi,1)$
at
![]() $z=1$
of the twisted Hasse–Weil L-series
$z=1$
of the twisted Hasse–Weil L-series
![]() $L(A,\psi,z)$
, associated to A and to finite dimensional complex characters
$L(A,\psi,z)$
, associated to A and to finite dimensional complex characters
![]() $\psi$
of the absolute Galois group of k, and the algebraic invariants of A. For instance, building on a conjecture due to Deligne and Gross concerning the order of vanishing at
$\psi$
of the absolute Galois group of k, and the algebraic invariants of A. For instance, building on a conjecture due to Deligne and Gross concerning the order of vanishing at
![]() $z=1$
of such functions one may, for a fixed character
$z=1$
of such functions one may, for a fixed character
![]() $\psi$
, predict that a suitable normalisation of
$\psi$
, predict that a suitable normalisation of
![]() $L^*(A,\psi,1)$
is algebraic and generates an explicit fractional ideal inside any large enough number field. See [Reference Burns and Macias Castillo10, Proposition. 7·3] for such explicit predictions.
$L^*(A,\psi,1)$
is algebraic and generates an explicit fractional ideal inside any large enough number field. See [Reference Burns and Macias Castillo10, Proposition. 7·3] for such explicit predictions.
However, even such conjectural formulas would not themselves account for any connections that might exist between the numbers
![]() $L^*(A,\psi,1)$
as
$L^*(A,\psi,1)$
as
![]() $\psi$
ranges over characters that are not necessarily in the same Galois orbit. In this direction, Mazur and Tate [Reference Mazur and Tate24] have, in certain concrete settings and by building on the theory of modular symbols, predicted explicit congruence relations between the values
$\psi$
ranges over characters that are not necessarily in the same Galois orbit. In this direction, Mazur and Tate [Reference Mazur and Tate24] have, in certain concrete settings and by building on the theory of modular symbols, predicted explicit congruence relations between the values
![]() $L(A,\psi,1)$
at
$L(A,\psi,1)$
at
![]() $z=1$
of the functions
$z=1$
of the functions
![]() $L(A,\psi,z)$
. In addition, Darmon [Reference Darmon17] has subsequently used the theory of Heegner points to formulate analogous predictions for the values
$L(A,\psi,z)$
. In addition, Darmon [Reference Darmon17] has subsequently used the theory of Heegner points to formulate analogous predictions for the values
![]() $L'(A,\psi,1)$
at
$L'(A,\psi,1)$
at
![]() $z=1$
of the first derivatives
$z=1$
of the first derivatives
![]() $L'(A,\psi,z)$
of the functions
$L'(A,\psi,z)$
of the functions
![]() $L(A,\psi,z)$
.
$L(A,\psi,z)$
.
Let F be a finite Galois extension of k. Then, in all cases, the congruence relations discussed in the previous paragraph, as
![]() $\psi$
ranges over complex irreducible characters of
$\psi$
ranges over complex irreducible characters of
![]() ${\rm Gal}(F/k)$
, involve the evaluation at suitable points of A(k) of the canonical
${\rm Gal}(F/k)$
, involve the evaluation at suitable points of A(k) of the canonical
![]() ${\rm Gal}(F/k)$
-valued height pairings that had been previously constructed by Mazur and Tate [Reference Mazur and Tate23] by using the geometrical theory of biextensions.
${\rm Gal}(F/k)$
-valued height pairings that had been previously constructed by Mazur and Tate [Reference Mazur and Tate23] by using the geometrical theory of biextensions.
In recent work [Reference Burns and Macias Castillo10] of Burns and the second author, a completely general framework for the conjectural theory of integral congruence relations between the leading terms
![]() $L^*(A,\psi,1)$
has been developed, thereby extending and refining the aforementioned conjectures of Mazur and Tate and of Darmon. This framework relies on the formulation of a completely general ‘refined conjecture of Birch and Swinnerton-Dyer type’ (or ‘refined BSD conjecture’ in the sequel) for A and
$L^*(A,\psi,1)$
has been developed, thereby extending and refining the aforementioned conjectures of Mazur and Tate and of Darmon. This framework relies on the formulation of a completely general ‘refined conjecture of Birch and Swinnerton-Dyer type’ (or ‘refined BSD conjecture’ in the sequel) for A and
![]() $F/k$
, which is then shown to encode general families of integral congruence relations involving the Mazur–Tate pairing.
$F/k$
, which is then shown to encode general families of integral congruence relations involving the Mazur–Tate pairing.
Fix F as above and set
![]() $G\;:\!=\;{\rm Gal}(F/k)$
. We let
$G\;:\!=\;{\rm Gal}(F/k)$
. We let
![]() $A_F$
denote the base change of A through
$A_F$
denote the base change of A through
![]() $F/k$
and consider
$F/k$
and consider
![]() $M_F \;:\!=\; h^1(A_F)(1)$
as a motive over k with a natural action of the semisimple
$M_F \;:\!=\; h^1(A_F)(1)$
as a motive over k with a natural action of the semisimple
![]() $\mathbb{Q}$
-algebra
$\mathbb{Q}$
-algebra
![]() $\mathbb{Q}[G]$
.
$\mathbb{Q}[G]$
.
It is then also shown in [Reference Burns and Macias Castillo10] that the refined BSD conjecture is equivalent to the equivariant Tamagawa number conjecture (or ‘eTNC’ in the sequel) for the pair
![]() $(M_F, {\mathbb{Z} [G]})$
, as formulated by Burns and Flach [Reference Burns and Flach7]. In addition, both of these conjectures decompose naturally into ‘p-components’, one for each rational prime number p, and each such component is itself of interest.
$(M_F, {\mathbb{Z} [G]})$
, as formulated by Burns and Flach [Reference Burns and Flach7]. In addition, both of these conjectures decompose naturally into ‘p-components’, one for each rational prime number p, and each such component is itself of interest.
For example, if A has good ordinary reduction at p, then the compatibility results proved by Burns and Venjakob [Reference Burns and Venjakob12] show that this p-component is (under certain hypotheses) a consequence of the main conjecture of non-commutative Iwasawa theory for A, as formulated by Coates et al. [Reference Coates, Fukaya, Kato, Sujatha and Venjakob16].
Assume now that p is a fixed odd prime and
![]() $F/k$
a cyclic p-extension of degree
$F/k$
a cyclic p-extension of degree
![]() $p^n$
for some natural number n. In this paper we will continue the study of the p-component of the eTNC that we begun in [Reference Bley and Macias Castillo6]. We recall that the main result of loc.cit. was the computation of an equivariant regulator under certain not-too-stringent conditions. Through this computation it was then possible to give a reformulation of this p-component which both was of theoretical interest and also made it amenable to providing partial numerical evidence.
$p^n$
for some natural number n. In this paper we will continue the study of the p-component of the eTNC that we begun in [Reference Bley and Macias Castillo6]. We recall that the main result of loc.cit. was the computation of an equivariant regulator under certain not-too-stringent conditions. Through this computation it was then possible to give a reformulation of this p-component which both was of theoretical interest and also made it amenable to providing partial numerical evidence.
For simplicity of the exposition, let us in the rest of this introduction assume that A is an elliptic curve. The computation of the equivariant regulator in [Reference Bley and Macias Castillo6] relied on the fact that, under suitable hypotheses, a representation-theoretic result due to Yakovlev [Reference Yakovlev31] implies that the p-completion
![]() $A(F)_p\;:\!=\;\mathbb Z_p\otimes_\mathbb Z A(F)$
of the Mordell–Weil group of A over F is a permutation
$A(F)_p\;:\!=\;\mathbb Z_p\otimes_\mathbb Z A(F)$
of the Mordell–Weil group of A over F is a permutation
![]() $\mathbb Z_p[G]$
-module. Explicitly speaking, this fact means that one may find points
$\mathbb Z_p[G]$
-module. Explicitly speaking, this fact means that one may find points
![]() $P_{(H,j)}\in A(F^H)$
, where H runs over all subgroups of G, with the property that
$P_{(H,j)}\in A(F^H)$
, where H runs over all subgroups of G, with the property that
![]() $\mathbb Z_p[G/H]\cdot P_{(H,j)}$
is a free
$\mathbb Z_p[G/H]\cdot P_{(H,j)}$
is a free
![]() $\mathbb Z_p[G/H]$
-module of rank one and also that
$\mathbb Z_p[G/H]$
-module of rank one and also that
 \begin{equation*} A(F)_p = \bigoplus_{H\leq G}\bigoplus_{j=1}^{m_H}\mathbb Z_p[G/H]\cdot P_{(H,j)}\end{equation*}
\begin{equation*} A(F)_p = \bigoplus_{H\leq G}\bigoplus_{j=1}^{m_H}\mathbb Z_p[G/H]\cdot P_{(H,j)}\end{equation*}
(for some set of non-negative integers
![]() $\{m_H:H\leq G\}$
).
$\{m_H:H\leq G\}$
).
However, our formula for the equivariant regulator involved a choice of an integral matrix
![]() $\Phi$
, with entries in
$\Phi$
, with entries in
![]() $\mathbb Z_p[G]$
, which depended upon a canonical extension class in the Yoneda 2-extension group
$\mathbb Z_p[G]$
, which depended upon a canonical extension class in the Yoneda 2-extension group
![]() ${\rm Ext}^2_{\mathbb Z_p[G]}({\textrm{Hom}}_{\mathbb Z_p}(A(F)_p,\mathbb Z_p),A(F)_p)$
and was therefore not computable in any examples unless this group vanished. Given the above direct sum decomposition of
${\rm Ext}^2_{\mathbb Z_p[G]}({\textrm{Hom}}_{\mathbb Z_p}(A(F)_p,\mathbb Z_p),A(F)_p)$
and was therefore not computable in any examples unless this group vanished. Given the above direct sum decomposition of
![]() $A(F)_p$
, the vanishing of this group holds if and only if
$A(F)_p$
, the vanishing of this group holds if and only if
![]() $m_H$
is equal to zero for each subgroup
$m_H$
is equal to zero for each subgroup
![]() $H\neq 1$
, or equivalently, if and only if
$H\neq 1$
, or equivalently, if and only if
![]() $A(F)_p$
is a free
$A(F)_p$
is a free
![]() $\mathbb Z_p[G]$
-module of the form
$\mathbb Z_p[G]$
-module of the form
![]() $\bigoplus_{j=1}^{m_1}\mathbb Z_p[G]\cdot P_{(1,j)}$
.
$\bigoplus_{j=1}^{m_1}\mathbb Z_p[G]\cdot P_{(1,j)}$
.
This limitation of our previous methods is consistent with those occurring in all existing verifications of p-components of the eTNC for any elliptic curves. Indeed, in the settings of the theoretical verifications obtained by the first author in [Reference Bley5], by Burns, Wuthrich and the second author in [Reference Burns, Macias Castillo and Wuthrich11], or of the recent extensions of these results by Burns and the second author in [Reference Burns and Macias Castillo10], as well as of the numerical verifications carried out in [Reference Bley3,Reference Bley4,Reference Burns, Macias Castillo and Wuthrich11] and in our previous paper [Reference Bley and Macias Castillo6], a full verification of this conjecture was only ever achieved in situations which forced the
![]() $\mathbb Z_p[G]$
-module
$\mathbb Z_p[G]$
-module
![]() $A(F)_p$
to be projective.
$A(F)_p$
to be projective.
On the other hand, even for
![]() $n=1$
(meaning that the extension
$n=1$
(meaning that the extension
![]() $F/k$
has degree p), the result [Reference Burns and Macias Castillo10, Theorem 9·11] shows that the p-component of the eTNC (or refined BSD conjecture) encodes a family of congruence relations between the leading terms
$F/k$
has degree p), the result [Reference Burns and Macias Castillo10, Theorem 9·11] shows that the p-component of the eTNC (or refined BSD conjecture) encodes a family of congruence relations between the leading terms
![]() $L^*(A,\psi,1)$
and certain ‘Mazur–Tate regulators’ (coming from the evaluation of Mazur–Tate height pairings) which are non-trivial unless
$L^*(A,\psi,1)$
and certain ‘Mazur–Tate regulators’ (coming from the evaluation of Mazur–Tate height pairings) which are non-trivial unless
![]() $A(F)_p$
is projective.
$A(F)_p$
is projective.
This observation is consistent with our previously encountered difficulties and also justifies why, from the point of view of our approach, it is only interesting to consider components of the general conjectures at primes which divide the degree of the extension.
In this paper we use a result of Burns and the second author [Reference Burns and Macias Castillo10, Theorem 10·3] to obtain an alternative computation of the equivariant regulator which is much better suited for the purpose of verifying ‘non-projective’ instances of the refined BSD conjecture.
To be a little more precise we note that, under our hypotheses, and for any subgroup H of G, the Mazur–Tate pairing for A considered over the sub-extension
![]() $F/F^H$
of
$F/F^H$
of
![]() $F/k$
gives a well defined pairing
$F/k$
gives a well defined pairing
Here
![]() $I_p(H)$
denotes the augmentation ideal in the group ring
$I_p(H)$
denotes the augmentation ideal in the group ring
![]() $\mathbb Z_p[H]$
and the isomorphism maps
$\mathbb Z_p[H]$
and the isomorphism maps
![]() $g\in H$
to the class of
$g\in H$
to the class of
![]() $g-1$
.
$g-1$
.
Fix any choice of points as above and any generator
![]() $\sigma$
of G. For any double-indices (H,j) and (J,i) with
$\sigma$
of G. For any double-indices (H,j) and (J,i) with
![]() $H,J\neq 1$
and
$H,J\neq 1$
and
![]() $H\leq J$
, we let
$H\leq J$
, we let
![]() $\Psi_{(H,j),(J,i)}$
be any element of
$\Psi_{(H,j),(J,i)}$
be any element of
![]() $\mathbb Z_p[G]$
which, in the group
$\mathbb Z_p[G]$
which, in the group
satisfies the equality
For double-indices with
![]() $J<H$
we will let
$J<H$
we will let
![]() $\Psi_{(H,j),(J,i)}$
be any element of
$\Psi_{(H,j),(J,i)}$
be any element of
![]() $\mathbb Z_p[G]$
which satisfies a straightforward variant of this equality. See (6) and Remark 2·3 below for more details.
$\mathbb Z_p[G]$
which satisfies a straightforward variant of this equality. See (6) and Remark 2·3 below for more details.
We then show that any matrix
![]() $\Psi$
obtained in this manner (by ordering all double-indices (H,j),(J,i) lexicographically) is, independently of all of the above choices, a suitable replacement for the essentially inexplicit matrix
$\Psi$
obtained in this manner (by ordering all double-indices (H,j),(J,i) lexicographically) is, independently of all of the above choices, a suitable replacement for the essentially inexplicit matrix
![]() $\Phi$
that occurred in the computation of the equivariant regulator in [Reference Bley and Macias Castillo6].
$\Phi$
that occurred in the computation of the equivariant regulator in [Reference Bley and Macias Castillo6].
In the main result of this paper, Theorem 2·1, we thus give a reformulation for the p-component of the refined BSD conjecture in terms of Mazur–Tate regulators obtained from considering natural components of the matrix
![]() $\Psi$
. This is in particular a suitable extension to general n of the result [Reference Burns and Macias Castillo10, Theorem 9·11] of Burns and the second author.
$\Psi$
. This is in particular a suitable extension to general n of the result [Reference Burns and Macias Castillo10, Theorem 9·11] of Burns and the second author.
As an application we are now able to obtain the first numerical verifications of the p-component of the refined BSD conjecture in situations in which the p-completed Mordell–Weil group
![]() $A(F)_p$
is not a projective
$A(F)_p$
is not a projective
![]() $\mathbb Z_p[G]$
-module. We emphasise again that there exists no other theoretical or numerical verification for this conjecture in such situations.
$\mathbb Z_p[G]$
-module. We emphasise again that there exists no other theoretical or numerical verification for this conjecture in such situations.
We shall give a detailed description, which we feel may be of some independent interest, of the methods that are appropriate to the numerical computation of Mazur–Tate pairings. We comment upon the results of our computations in Section 4·4. Here we also give a list of pairs
![]() $(A,F/k)$
for which we have numerically verified the conjecture, although this list is not exhaustive. See also the webpage of the first author for more details and the MAGMA implementation.
$(A,F/k)$
for which we have numerically verified the conjecture, although this list is not exhaustive. See also the webpage of the first author for more details and the MAGMA implementation.
1·1. General notation
For a finite abelian group
![]() $\Gamma$
we set
$\Gamma$
we set
![]() ${\rm Tr}_\Gamma\;:\!=\;\sum_{\gamma \in \Gamma} \gamma\in\mathbb Z[\Gamma]$
and also
${\rm Tr}_\Gamma\;:\!=\;\sum_{\gamma \in \Gamma} \gamma\in\mathbb Z[\Gamma]$
and also
![]() $\widehat{\Gamma}\;:\!=\;{\textrm{Hom}}_\mathbb Z(\Gamma,\mathbb C^\times)$
. We write
$\widehat{\Gamma}\;:\!=\;{\textrm{Hom}}_\mathbb Z(\Gamma,\mathbb C^\times)$
. We write
![]() $\check\psi$
for the contragrediant character of each
$\check\psi$
for the contragrediant character of each
![]() $\psi \in \hat{\Gamma}$
and also write
$\psi \in \hat{\Gamma}$
and also write
for the associated idempotent.
For any abelian group M we let
![]() $M_{{\rm tor}}$
denote its torsion subgroup. We also set
$M_{{\rm tor}}$
denote its torsion subgroup. We also set
![]() $M_p \;:\!=\; {\mathbb{Z}_p} \otimes_{\mathbb{Z}} M$
. If M is finitely generated, then for a field extension E of
$M_p \;:\!=\; {\mathbb{Z}_p} \otimes_{\mathbb{Z}} M$
. If M is finitely generated, then for a field extension E of
![]() $\mathbb{Q}$
we shall sometimes abbreviate
$\mathbb{Q}$
we shall sometimes abbreviate
![]() $E \otimes_{\mathbb{Z}} M$
to
$E \otimes_{\mathbb{Z}} M$
to
![]() $E \cdot M$
. Finally, for any integer n we write M[n] for the subgroup of n-torsion points of M.
$E \cdot M$
. Finally, for any integer n we write M[n] for the subgroup of n-torsion points of M.
For any
![]() ${\mathbb{Z}_p}[\Gamma]$
-Module M we write
${\mathbb{Z}_p}[\Gamma]$
-Module M we write
![]() $M^*$
for the linear dual
$M^*$
for the linear dual
![]() ${\textrm{Hom}}_{\mathbb{Z}_p}(M, {\mathbb{Z}_p})$
, endowed with the natural contragredient action of
${\textrm{Hom}}_{\mathbb{Z}_p}(M, {\mathbb{Z}_p})$
, endowed with the natural contragredient action of
![]() $\Gamma$
. Explicitly, for a homomorphism f and elements
$\Gamma$
. Explicitly, for a homomorphism f and elements
![]() $m \in M$
and
$m \in M$
and
![]() $\gamma \in \Gamma$
, one has
$\gamma \in \Gamma$
, one has
![]() $(\gamma f)(m) = f(\gamma^{-1} m)$
. If
$(\gamma f)(m) = f(\gamma^{-1} m)$
. If
![]() $\Delta$
is a subgroup of
$\Delta$
is a subgroup of
![]() $\Gamma$
, we write
$\Gamma$
, we write
![]() $M_\Delta$
for the module of
$M_\Delta$
for the module of
![]() $\Delta$
-coinvariants of M.
$\Delta$
-coinvariants of M.
For any Galois extension of fields we abbreviate
![]() ${\textrm{Gal}}(L/K)$
to
${\textrm{Gal}}(L/K)$
to
![]() $G_{L/K}$
. We fix an algebraic closure
$G_{L/K}$
. We fix an algebraic closure
![]() $K^c$
of K and abbreviate
$K^c$
of K and abbreviate
![]() $G_{K^c/K}$
to
$G_{K^c/K}$
to
![]() $G_K$
.
$G_K$
.
If A is an abelian variety defined over a number field k and
![]() $L/k$
a finite extension, we write A(L) for the Mordell–Weil group,
$L/k$
a finite extension, we write A(L) for the Mordell–Weil group,
![]() ${\rm{III(}}{A_L}{\rm{)}}$
for the Tate–Shafarevich group of A over L and
${\rm{III(}}{A_L}{\rm{)}}$
for the Tate–Shafarevich group of A over L and
![]() ${\rm{II}}{{\rm{I}}_p}{\rm{(}}{A_L}{\rm{)}}$
for its p-primary part.
${\rm{II}}{{\rm{I}}_p}{\rm{(}}{A_L}{\rm{)}}$
for its p-primary part.
2. Statement of the main result
In this section we state our standing hypotheses and, after defining all the relevant objects, state the main result of this paper.
2·1. The hypotheses
Let A be an abelian variety of dimension d, defined over a number field k. Let p be an odd prime number and let
![]() $F/k$
be a cyclic field extension of degree
$F/k$
be a cyclic field extension of degree
![]() $p^n$
, for some natural number n. We write
$p^n$
, for some natural number n. We write
![]() $A^t$
for the dual abelian variety.
$A^t$
for the dual abelian variety.
As in [Reference Bley and Macias Castillo6, Section 2], we will assume the validity of the following list of hypotheses:
-
(a)
 $p \nmid |A(k)_{\rm tor}| \cdot |A^t(k)_{\rm tor}|$
;
$p \nmid |A(k)_{\rm tor}| \cdot |A^t(k)_{\rm tor}|$
; -
(b) p does not divide the Tamagawa number of A at any place of k at which it has bad reduction;
-
(c) has good reduction at all p-adic places of k;
-
(d) p is unramified in
 $F/\mathbb Q$
;
$F/\mathbb Q$
; -
(e) no place of bad reduction of A is ramified in
 $F/k$
;
$F/k$
; -
(f) if a place v of k ramifies in
 $F/k$
then no point of order p of the reduction of A is defined over the residue field of v;
$F/k$
then no point of order p of the reduction of A is defined over the residue field of v; -
(g)
 ${\rm{III}}(A_{F})$
is finite;
${\rm{III}}(A_{F})$
is finite; -
(h)
 ${\rm{III}}_p(A_{F^H})$
vanishes for all non-trivial subgroups H of G;
${\rm{III}}_p(A_{F^H})$
vanishes for all non-trivial subgroups H of G; -
(i) the group
 $H^1({\textrm{Gal}}(k(A[p^n])/k),A[p^n])$
vanishes.
$H^1({\textrm{Gal}}(k(A[p^n])/k),A[p^n])$
vanishes.
Remark 2·1. The hypotheses (a)-(h) recover those in place throughout [Reference Bley and Macias Castillo6]. The full list of hypotheses also recovers those that are in place in [Reference Burns and Macias Castillo10, Theorem 9·9 and 9·11]. We refer the reader to [Reference Bley and Macias Castillo6, Remark 2·1] or [Reference Burns and Macias Castillo10, Remark 6·1] for a further discussion of these hypotheses.
The hypothesis (i) recovers hypothesis 10·1 from [Reference Burns and Macias Castillo10] in our setting and will hence allow us to apply Theorem 10·3 of loc. cit. We recall that it is widely satisfied. For instance, it holds whenever multiplication-by-‘
![]() $-1$
’ belongs to the image of the canonical Galois representation
$-1$
’ belongs to the image of the canonical Galois representation
![]() $G_k\to{\rm Aut}_{\mathbb{F}_p}(A[p])$
. In particular, if A is an elliptic curve then this hypothesis excludes only finitely many primes, by a result of Serre. Moreover, if A is an elliptic curve and k does not contain any p-th roots of unity, Lawson and Wuthrich have recently shown that hypothesis (i) is valid in all but certain exceptional cases that, in particular, all have
$G_k\to{\rm Aut}_{\mathbb{F}_p}(A[p])$
. In particular, if A is an elliptic curve then this hypothesis excludes only finitely many primes, by a result of Serre. Moreover, if A is an elliptic curve and k does not contain any p-th roots of unity, Lawson and Wuthrich have recently shown that hypothesis (i) is valid in all but certain exceptional cases that, in particular, all have
![]() $p\leq 11$
(see [Reference Lawson, Wuthrich, Loeffler and Zerbes21, Theorem 2, Section 6]).
$p\leq 11$
(see [Reference Lawson, Wuthrich, Loeffler and Zerbes21, Theorem 2, Section 6]).
Remark 2·2. It is possible, using computations in [Reference Burns and Macias Castillo10], to obtain a generalisation of our main result under a significantly weaker version of hypotheses (d) (that still ensures the surjectivity of the appropriate norm maps on Mordell–Weil groups).
Our main result will concern an ‘equivariant regulator’
![]() ${\rm Reg}_{A,F/k,j}$
in
${\rm Reg}_{A,F/k,j}$
in
![]() $\mathbb C_p[G]^\times/\mathbb Z_p[G]^\times$
for each isomorphism
$\mathbb C_p[G]^\times/\mathbb Z_p[G]^\times$
for each isomorphism
![]() $j:\mathbb C\cong\mathbb C_p$
, which we now proceed to define. Throughout the construction of this element, we will always use j to implicitly identify
$j:\mathbb C\cong\mathbb C_p$
, which we now proceed to define. Throughout the construction of this element, we will always use j to implicitly identify
![]() $\widehat G$
with
$\widehat G$
with
![]() ${\textrm{Hom}}_\mathbb Z(G,\mathbb C_p^\times)$
.
${\textrm{Hom}}_\mathbb Z(G,\mathbb C_p^\times)$
.
2·2. Néron–Tate regulators
For
![]() $0\leq r\leq n$
we denote by
$0\leq r\leq n$
we denote by
![]() $J_r$
the subgroup of G of order
$J_r$
the subgroup of G of order
![]() $p^{n-r}$
and set
$p^{n-r}$
and set
![]() $F_r\;:\!=\;F^{J_r}$
and
$F_r\;:\!=\;F^{J_r}$
and
![]() $\Gamma_r\;:\!=\;G/J_r$
. Clearly,
$\Gamma_r\;:\!=\;G/J_r$
. Clearly,
![]() $[F_r:k] = |\Gamma_r| = p^r$
.
$[F_r:k] = |\Gamma_r| = p^r$
.
Our hypotheses allow us to apply a result of Yakovlev [Reference Yakovlev31] in order to restrict the Galois structure of the Mordell–Weil groups
![]() $A(F)_p$
and
$A(F)_p$
and
![]() $A^t(F)_p$
as follows. For any natural number m we write [m] for the set
$A^t(F)_p$
as follows. For any natural number m we write [m] for the set
![]() $\{1,\ldots,m\}$
.
$\{1,\ldots,m\}$
.
By [Reference Bley and Macias Castillo6, Proposition 2·2 and (2·1)] we may and will fix a set of non-negative integers
![]() $\{m_{r}:0\leq r\leq n\}$
and subsets
$\{m_{r}:0\leq r\leq n\}$
and subsets
such that the
![]() $\mathbb Z_p[\Gamma_r]$
-modules generated by each of the points
$\mathbb Z_p[\Gamma_r]$
-modules generated by each of the points
![]() $P_{(r,j)}$
and
$P_{(r,j)}$
and
![]() $P^t_{(r,j)}$
are free of rank one and there are direct sum decompositions of
$P^t_{(r,j)}$
are free of rank one and there are direct sum decompositions of
![]() $\mathbb Z_p[G]$
-modules
$\mathbb Z_p[G]$
-modules
 \begin{equation} A(F)_p = \bigoplus_{r=0}^{n}\bigoplus_{j=1}^{m_r}\mathbb Z_p[\Gamma_r]\cdot P_{(r,j)} \,\,\text{ and }\,\, A^t(F)_p = \bigoplus_{r=0}^{n}\bigoplus_{j=1}^{m_r}\mathbb Z_p[\Gamma_r]\cdot P^t_{(r,j)}.\end{equation}
\begin{equation} A(F)_p = \bigoplus_{r=0}^{n}\bigoplus_{j=1}^{m_r}\mathbb Z_p[\Gamma_r]\cdot P_{(r,j)} \,\,\text{ and }\,\, A^t(F)_p = \bigoplus_{r=0}^{n}\bigoplus_{j=1}^{m_r}\mathbb Z_p[\Gamma_r]\cdot P^t_{(r,j)}.\end{equation}
We set
 \begin{equation*}\mathcal{P} \;:\!=\; \bigcup_{r=0}^n \mathcal{P}_{(r)}, \quad \mathcal{P}^t \;:\!=\; \bigcup_{r=0}^n \mathcal{P}^t_{(r)}.\end{equation*}
\begin{equation*}\mathcal{P} \;:\!=\; \bigcup_{r=0}^n \mathcal{P}_{(r)}, \quad \mathcal{P}^t \;:\!=\; \bigcup_{r=0}^n \mathcal{P}^t_{(r)}.\end{equation*}
By ordering our fixed choice of points
![]() $\mathcal{P}$
and
$\mathcal{P}$
and
![]() $\mathcal{P}^t$
lexicographically, we obtain a ‘regulator matrix’
$\mathcal{P}^t$
lexicographically, we obtain a ‘regulator matrix’
 \begin{equation*}R_{A,F/k}^{\rm NT}(\mathcal{P}, \mathcal{P}^t)\;:\!=\;\left( \sum_{g \in G}\langle gP^t_{(r,j)},P_{(s,i)}\rangle_{A_F}\cdot g^{-1} \right)_{(r,j),(s,i)}\in M_N(\mathbb R[G])\end{equation*}
\begin{equation*}R_{A,F/k}^{\rm NT}(\mathcal{P}, \mathcal{P}^t)\;:\!=\;\left( \sum_{g \in G}\langle gP^t_{(r,j)},P_{(s,i)}\rangle_{A_F}\cdot g^{-1} \right)_{(r,j),(s,i)}\in M_N(\mathbb R[G])\end{equation*}
with
![]() $N \;:\!=\; \sum_{r=0}^n m_r$
, and where
$N \;:\!=\; \sum_{r=0}^n m_r$
, and where
![]() $\langle -,-\rangle_{A_F}$
denotes the Néron–Tate height pairing for A over F.
$\langle -,-\rangle_{A_F}$
denotes the Néron–Tate height pairing for A over F.
For any matrix
![]() $X=(x_{(r,j), (s,i)})$
where the indices
$X=(x_{(r,j), (s,i)})$
where the indices
![]() $\{ (r,j) : 0\leq r \leq n, j\in[m_r] \}$
are ordered lexicographically and for any
$\{ (r,j) : 0\leq r \leq n, j\in[m_r] \}$
are ordered lexicographically and for any
![]() $0\leq t\leq n$
, we set
$0\leq t\leq n$
, we set
and, given any matrix Y with entries in
![]() $\mathbb C[G]$
, resp.
$\mathbb C[G]$
, resp.
![]() $\mathbb C_p[G]$
, and any
$\mathbb C_p[G]$
, and any
![]() $\psi\in\widehat G$
, we write
$\psi\in\widehat G$
, we write
![]() $\psi(Y)$
for the matrix with entries in
$\psi(Y)$
for the matrix with entries in
![]() $\mathbb C$
, resp.
$\mathbb C$
, resp.
![]() $\mathbb C_p$
, obtained after extending
$\mathbb C_p$
, obtained after extending
![]() $\psi$
to a function on
$\psi$
to a function on
![]() $\mathbb C[G]$
, resp.
$\mathbb C[G]$
, resp.
![]() $\mathbb C_p[G]$
, by linearity and then evaluating
$\mathbb C_p[G]$
, by linearity and then evaluating
![]() $\psi$
at each entry of Y. For any
$\psi$
at each entry of Y. For any
![]() $\psi\in\widehat{G}$
we define an integer
$\psi\in\widehat{G}$
we define an integer
![]() $t_\psi$
between 0 and n by the equality
$t_\psi$
between 0 and n by the equality
![]() $\ker(\psi) = J_{t_\psi}$
and then set
$\ker(\psi) = J_{t_\psi}$
and then set
We now put
 \begin{equation*}m_{\psi}\;:\!=\;\sum_{r=t_\psi}^{n}(n-r)m_r\end{equation*}
\begin{equation*}m_{\psi}\;:\!=\;\sum_{r=t_\psi}^{n}(n-r)m_r\end{equation*}
and define the
![]() $\psi$
-component of the equivariant Néron–Tate regulator by
$\psi$
-component of the equivariant Néron–Tate regulator by
Each regulator term
![]() ${\rm Reg}^{\rm NT}_\psi(\mathcal{P}, \mathcal{P}^t)$
coincides with the element
${\rm Reg}^{\rm NT}_\psi(\mathcal{P}, \mathcal{P}^t)$
coincides with the element
![]() $\lambda_\psi(\mathcal{P}, \mathcal{P}^t)$
defined in [Reference Bley and Macias Castillo6, Definition 2·4].
$\lambda_\psi(\mathcal{P}, \mathcal{P}^t)$
defined in [Reference Bley and Macias Castillo6, Definition 2·4].
We finally fix a generator
![]() $\sigma$
of G and then define a non-zero complex number
$\sigma$
of G and then define a non-zero complex number
 \begin{equation}\delta_\psi\;:\!=\;\prod_{r=0}^{t_\psi-1}\left(\psi(\sigma)^{p^r}-1\right)^{m_r}.\end{equation}
\begin{equation}\delta_\psi\;:\!=\;\prod_{r=0}^{t_\psi-1}\left(\psi(\sigma)^{p^r}-1\right)^{m_r}.\end{equation}
2·3. Mazur–Tate regulators
For any
![]() $0 \le r \le n$
we recall that, under our given hypotheses, [Reference Burns and Macias Castillo10, Proposition 6·3(ii)] implies that every element of
$0 \le r \le n$
we recall that, under our given hypotheses, [Reference Burns and Macias Castillo10, Proposition 6·3(ii)] implies that every element of
![]() $A^t(F_r)_p$
and
$A^t(F_r)_p$
and
![]() $A(F_r)_p$
is ‘locally-normed’. Indeed, from this result one knows that for every finite prime w of F, the G-modules
$A(F_r)_p$
is ‘locally-normed’. Indeed, from this result one knows that for every finite prime w of F, the G-modules
![]() $\mathbb Z_p\otimes_\mathbb Z A^t(F_w)$
and
$\mathbb Z_p\otimes_\mathbb Z A^t(F_w)$
and
![]() $\mathbb Z_p\otimes_\mathbb Z A(F_w)$
are cohomologically-trivial and from this it follows easily that the p-completions of the subgroups of locally-normed elements in
$\mathbb Z_p\otimes_\mathbb Z A(F_w)$
are cohomologically-trivial and from this it follows easily that the p-completions of the subgroups of locally-normed elements in
![]() $A^t(F_r)$
and in
$A^t(F_r)$
and in
![]() $A(F_r)$
are equal to the full p-completions
$A(F_r)$
are equal to the full p-completions
![]() $A^t(F_r)_p$
and
$A^t(F_r)_p$
and
![]() $A(F_r)_p$
, respectively.
$A(F_r)_p$
, respectively.
In particular, the construction of Mazur and Tate using the theory of biextensions gives well defined canonical height pairings
Here
![]() $I_p(J_r)$
denotes the augmentation ideal in the group ring
$I_p(J_r)$
denotes the augmentation ideal in the group ring
![]() $\mathbb Z_p[J_r]$
and the isomorphism maps
$\mathbb Z_p[J_r]$
and the isomorphism maps
![]() $g\in J_r$
to the class of
$g\in J_r$
to the class of
![]() $g-1$
.
$g-1$
.
In the sequel we also write
![]() $\rho_r$
for the canonical projection
$\rho_r$
for the canonical projection
![]() $\mathbb Z_p[G]\to\mathbb Z_p[\Gamma_r]$
. For any indices
$\mathbb Z_p[G]\to\mathbb Z_p[\Gamma_r]$
. For any indices
![]() $0\leq r,s\leq n-1$
, any
$0\leq r,s\leq n-1$
, any
![]() $j\in[m_r]$
and any
$j\in[m_r]$
and any
![]() $i\in[m_s]$
, we set
$i\in[m_s]$
, we set
![]() $\ell\;:\!=\;{\rm max}(r,s)$
and then fix any elements
$\ell\;:\!=\;{\rm max}(r,s)$
and then fix any elements
![]() $\Psi_{(r,j),(s,i)}$
of
$\Psi_{(r,j),(s,i)}$
of
![]() $\mathbb Z_p[G]$
which satisfy the equality
$\mathbb Z_p[G]$
which satisfy the equality
in
It will be clear from Proposition 3·2 below that such elements always exist.
Remark 2·3. Let
![]() $\mathcal I_p(J_r)$
denote the ideal of
$\mathcal I_p(J_r)$
denote the ideal of
![]() $\mathbb Z_p[G]$
generated by
$\mathbb Z_p[G]$
generated by
![]() $I_p(J_r)$
. Then the inclusion
$I_p(J_r)$
. Then the inclusion
![]() $I_p(J_\ell)\subset I_p(J_r)$
induces a canonical inclusion
$I_p(J_\ell)\subset I_p(J_r)$
induces a canonical inclusion
Here the isomorphism is canonical (see [Reference Burns, Kurihara and Sano8, Proposition 4·9]). It is then clear that the left-hand side of the equality (6) coincides with the class of
![]() $\Psi_{(r,j),(s,i)}\cdot(\sigma^{p^\ell}-1)$
in the quotient
$\Psi_{(r,j),(s,i)}\cdot(\sigma^{p^\ell}-1)$
in the quotient
![]() $\mathcal I_p(J_r)/\mathcal I_p(J_r)^2$
.
$\mathcal I_p(J_r)/\mathcal I_p(J_r)^2$
.
Using these choices we construct a matrix
 \begin{equation}\Psi(\mathcal{P}, \mathcal{P}^t)\;:\!=\;\left( \begin{array}{cc|c}\left(\Psi_{(r,j),(s,i)} \right)_{r,s < n} & & \begin{array}{c} 0\\\vdots\\0 \end{array}\\ \hline \begin{array}{ccc} 0 & \ldots & 0 \end{array} && I_{m_{n}}\end{array}\right)\end{equation}
\begin{equation}\Psi(\mathcal{P}, \mathcal{P}^t)\;:\!=\;\left( \begin{array}{cc|c}\left(\Psi_{(r,j),(s,i)} \right)_{r,s < n} & & \begin{array}{c} 0\\\vdots\\0 \end{array}\\ \hline \begin{array}{ccc} 0 & \ldots & 0 \end{array} && I_{m_{n}}\end{array}\right)\end{equation}
with entries in
![]() $\mathbb Z_p[G]$
. Here
$\mathbb Z_p[G]$
. Here
![]() $I_{m_n}$
denotes the identity
$I_{m_n}$
denotes the identity
![]() $m_n\times m_n$
matrix.
$m_n\times m_n$
matrix.
For any
![]() $\psi\in\widehat G$
, Lemma 3·4 below will show that the element
$\psi\in\widehat G$
, Lemma 3·4 below will show that the element
of
![]() $\mathbb C_p[G]$
belongs to
$\mathbb C_p[G]$
belongs to
![]() $\mathbb C_p[G]^\times$
(so in particular each term
$\mathbb C_p[G]^\times$
(so in particular each term
![]() $\varepsilon_\psi(\Psi(\mathcal{P},\mathcal{P}^t))$
is non-zero) and is independent, up to multiplication by an element of
$\varepsilon_\psi(\Psi(\mathcal{P},\mathcal{P}^t))$
is non-zero) and is independent, up to multiplication by an element of
![]() $\mathbb Z_p[G]^\times$
, of the choices made in (6).
$\mathbb Z_p[G]^\times$
, of the choices made in (6).
2·4. The equivariant regulator
We may now define our equivariant regulator. We again set
![]() $N\;:\!=\;\sum_{r=0}^{n}m_r$
.
$N\;:\!=\;\sum_{r=0}^{n}m_r$
.
Definition 2·4. For a fixed isomorphism
![]() $j \colon {\mathbb{C}} \to {\mathbb{C}_p}$
, the class of
$j \colon {\mathbb{C}} \to {\mathbb{C}_p}$
, the class of
 \begin{equation}{\rm Reg}_{A, F/k, j} \;:\!=\;(-1)^{N-m_n}\cdot \sum_{\psi \in \widehat G}\frac{j({\rm Reg}^{\rm NT}_\psi(\mathcal{P}, \mathcal{P}^t) \cdot \delta_\psi)} {\varepsilon_{\psi}(\Psi(\mathcal{P},\mathcal{P}^t))}\cdot e_\psi\end{equation}
\begin{equation}{\rm Reg}_{A, F/k, j} \;:\!=\;(-1)^{N-m_n}\cdot \sum_{\psi \in \widehat G}\frac{j({\rm Reg}^{\rm NT}_\psi(\mathcal{P}, \mathcal{P}^t) \cdot \delta_\psi)} {\varepsilon_{\psi}(\Psi(\mathcal{P},\mathcal{P}^t))}\cdot e_\psi\end{equation}
in
![]() $\mathbb{C}_p[G]^\times / \mathbb{Z}_p[G]^\times$
is the (p-primary) equivariant regulator associated to A and
$\mathbb{C}_p[G]^\times / \mathbb{Z}_p[G]^\times$
is the (p-primary) equivariant regulator associated to A and
![]() $F/k$
.
$F/k$
.
The claims made in Section 2·3 imply that
![]() ${\rm Reg}_{A, F/k, j}$
is independent of the choices of
${\rm Reg}_{A, F/k, j}$
is independent of the choices of
![]() $\mathcal{P}, \mathcal{P}^t, \sigma$
and the matrix
$\mathcal{P}, \mathcal{P}^t, \sigma$
and the matrix
![]() $\Psi(\mathcal{P}, \mathcal{P}^t)$
. By abuse of terminology we will often refer to any choice of
$\Psi(\mathcal{P}, \mathcal{P}^t)$
. By abuse of terminology we will often refer to any choice of
![]() ${\rm Reg}_{A, F/k, j}$
in
${\rm Reg}_{A, F/k, j}$
in
![]() $\mathbb{C}_p[G]^\times$
itself as the equivariant regulator.
$\mathbb{C}_p[G]^\times$
itself as the equivariant regulator.
Remark 2·5. The results of Proposition 3·2 and Lemma 3·4 below combine to show that
![]() ${\rm Reg}_{A, F/k, j}$
is precisely the element
${\rm Reg}_{A, F/k, j}$
is precisely the element
which occurs in [Reference Bley and Macias Castillo6, Theorem 2·9]. The main new insight is that the elements
![]() $\varepsilon_\psi(\Phi) \in {\mathbb{C}}_p^\times$
which depended upon an essentially unknown matrix
$\varepsilon_\psi(\Phi) \in {\mathbb{C}}_p^\times$
which depended upon an essentially unknown matrix
![]() $\Phi \in M_N(\mathbb{Z}_p[G])$
can be explicitly determined by (6).
$\Phi \in M_N(\mathbb{Z}_p[G])$
can be explicitly determined by (6).
2·5. Statement of the result
The refined Birch and Swinnerton–Dyer conjecture is an equality between analytic and algebraic invariants associated with
![]() $A/k$
and
$A/k$
and
![]() $F/k$
. We now briefly describe the analytic part refering the reader to [Reference Bley and Macias Castillo6, Section 2] or [Reference Burns and Macias Castillo10] for further details.
$F/k$
. We now briefly describe the analytic part refering the reader to [Reference Bley and Macias Castillo6, Section 2] or [Reference Burns and Macias Castillo10] for further details.
For each
![]() $\psi \in \widehat{G}$
we set
$\psi \in \widehat{G}$
we set
 \begin{equation*} \mathcal L_\psi^* = \mathcal L_{A, F/k, \psi}^* \;:\!=\; \frac{L_{S_{\rm r}}^*(A, \check{\psi}, 1) \cdot \tau^*(\mathbb{Q}, {\rm ind}_k^{\rm Q}(\psi))^d }{\Omega_A^\psi\cdot w_\psi^d} \in {\mathbb{C}}^\times,\end{equation*}
\begin{equation*} \mathcal L_\psi^* = \mathcal L_{A, F/k, \psi}^* \;:\!=\; \frac{L_{S_{\rm r}}^*(A, \check{\psi}, 1) \cdot \tau^*(\mathbb{Q}, {\rm ind}_k^{\rm Q}(\psi))^d }{\Omega_A^\psi\cdot w_\psi^d} \in {\mathbb{C}}^\times,\end{equation*}
where;
-
(i)
 $L^*_{S_r}(A, \psi, 1)$
is the leading term in the Taylor expansion at
$L^*_{S_r}(A, \psi, 1)$
is the leading term in the Taylor expansion at
 $z=1$
of the
$z=1$
of the
 $\psi$
-twisted Hasse–Weil L-function
$\psi$
-twisted Hasse–Weil L-function
 $L_{S_r}(A,\psi,z)$
of A, truncated by removing the Euler factors corresponding to the set
$L_{S_r}(A,\psi,z)$
of A, truncated by removing the Euler factors corresponding to the set
 $S_{{\rm r}}$
of primes of k which ramify in
$S_{{\rm r}}$
of primes of k which ramify in
 $F/k$
;
$F/k$
; -
(ii)
 $\tau^*(\mathbb{Q}, {\rm ind}_k^{\rm Q}(\psi))$
is a suitably modified global Galois–Gauss sum;
$\tau^*(\mathbb{Q}, {\rm ind}_k^{\rm Q}(\psi))$
is a suitably modified global Galois–Gauss sum; -
(iii)
 $\Omega_A^\psi\cdot w_\psi^d$
is a (suitably normalised) product of periods.
$\Omega_A^\psi\cdot w_\psi^d$
is a (suitably normalised) product of periods.
We finally set
and note that the element
![]() $\mathcal L^*$
defined immediately above [Reference Burns and Macias Castillo10, Theorem 6·5] specialises precisely to our definition.
$\mathcal L^*$
defined immediately above [Reference Burns and Macias Castillo10, Theorem 6·5] specialises precisely to our definition.
Without any further mention we will always assume that the functions
![]() $L_{S_r}(A,\psi,z)$
have analytic continuation to
$L_{S_r}(A,\psi,z)$
have analytic continuation to
![]() $z=1$
, so that the above term is well-defined. We also recall that Deligne and Gross have then predicted that these functions should vanish at
$z=1$
, so that the above term is well-defined. We also recall that Deligne and Gross have then predicted that these functions should vanish at
![]() $z=1$
exactly to order equal to the multiplicity with which the character
$z=1$
exactly to order equal to the multiplicity with which the character
![]() $\psi$
occurs in the representation
$\psi$
occurs in the representation
![]() $\mathbb C\otimes_\mathbb Z A^t(F)$
of G.
$\mathbb C\otimes_\mathbb Z A^t(F)$
of G.
We now formulate the main result of this manuscript. For any
![]() $j\;:\;\mathbb C\cong\mathbb C_p$
we write
$j\;:\;\mathbb C\cong\mathbb C_p$
we write
![]() $j_*$
for the associated map
$j_*$
for the associated map
![]() $\mathbb C[G]^\times\to \mathbb C_p[G]^\times$
.
$\mathbb C[G]^\times\to \mathbb C_p[G]^\times$
.
Theorem 2·1. Assume that the hypotheses (a)–(i) are valid. Let
![]() $\mathcal{P}$
and
$\mathcal{P}$
and
![]() $\mathcal{P}^t$
be any choice of points such that (1) holds. Assume also that
$\mathcal{P}^t$
be any choice of points such that (1) holds. Assume also that
![]() ${\rm{III}}_p(A_F) = 0$
.
${\rm{III}}_p(A_F) = 0$
.
Then the p-component of the refined Birch and Swinnerton–Dyer conjecture is valid if and only if, for any
![]() $j\;:\;\mathbb C\cong\mathbb C_p$
, the element
$j\;:\;\mathbb C\cong\mathbb C_p$
, the element
 \begin{equation}\frac{j_*\left( \mathcal L^*_{A, F/k} \right)}{ {\rm Reg}_{A, F/k, j} }\end{equation}
\begin{equation}\frac{j_*\left( \mathcal L^*_{A, F/k} \right)}{ {\rm Reg}_{A, F/k, j} }\end{equation}
belongs to
![]() $\mathbb{Z}_p[G]^\times$
.
$\mathbb{Z}_p[G]^\times$
.
Remark 2·6. One may rephrase the condition that the element (11) belongs to
![]() $\mathbb Z_p[G]^\times$
in terms of explicit congruence relations in the augmentation filtration, as occurring in [Reference Macias Castillo22, Conjecture 3·11].
$\mathbb Z_p[G]^\times$
in terms of explicit congruence relations in the augmentation filtration, as occurring in [Reference Macias Castillo22, Conjecture 3·11].
The proof of Theorem 2·1 will occupy the next section.
3. The proof of Theorem 2.1
Under our listed hypotheses, in [Reference Burns and Macias Castillo10, Theorem 6·5 and Remark 6·6] reformulate the p-component of the refined BSD conjecture (denoted by
![]() ${\rm BSD}_p(A_{F/k})$
throughout loc. cit.) as an equality of the form
${\rm BSD}_p(A_{F/k})$
throughout loc. cit.) as an equality of the form
in the relative algebraic K-group
![]() $K_0(\mathbb Z_p[G],\mathbb C_p[G])$
. Here
$K_0(\mathbb Z_p[G],\mathbb C_p[G])$
. Here
is the canonical ‘extended boundary homomorphism’ considered by Burns and Flach in [Reference Burns and Flach7, Section 4·2] while the right-hand side is the refined Euler characteristic of the pair
![]() $({\rm SC}_p(A_{F/k}),h_{A,F}^j)$
. We thus also recall that
$({\rm SC}_p(A_{F/k}),h_{A,F}^j)$
. We thus also recall that
![]() ${\rm SC}_p(A_{F/k})$
is the ‘classical p-adic Selmer complex’ for A and
${\rm SC}_p(A_{F/k})$
is the ‘classical p-adic Selmer complex’ for A and
![]() $F/k$
, as defined [Reference Burns and Macias Castillo10, Definition 2.3], while
$F/k$
, as defined [Reference Burns and Macias Castillo10, Definition 2.3], while
![]() $h_{A,F}^j$
is the canonical trivialisation of this complex that is induced by the Néron–Tate height (see below).
$h_{A,F}^j$
is the canonical trivialisation of this complex that is induced by the Néron–Tate height (see below).
At the outset we set
![]() $C\;:\!=\;{\rm SC}_p(A_{F/k})$
and note that, under the hypotheses of Theorem 2·1, it is proved in [Reference Burns and Macias Castillo10, Proposition 6·3] that C is a perfect complex of
$C\;:\!=\;{\rm SC}_p(A_{F/k})$
and note that, under the hypotheses of Theorem 2·1, it is proved in [Reference Burns and Macias Castillo10, Proposition 6·3] that C is a perfect complex of
![]() $\mathbb Z_p[G]$
-modules. In addition, there are canonical identifications
$\mathbb Z_p[G]$
-modules. In addition, there are canonical identifications
 \begin{equation} r_i:H^i(C)\cong\begin{cases}A^t(F)_p, & i=1;\\ A(F)_p^*, & i=2;\\ 0, & i \ne 1,2. \end{cases}\end{equation}
\begin{equation} r_i:H^i(C)\cong\begin{cases}A^t(F)_p, & i=1;\\ A(F)_p^*, & i=2;\\ 0, & i \ne 1,2. \end{cases}\end{equation}
The trivialisation
is then the canonical isomorphism induced by the Néron–Tate height pairing via (12) and j.
We now rephrase the validity of the p-component of the refined BSD conjecture as the vanishing of the element
of
![]() $K_0(\mathbb Z_p[G],\mathbb C_p[G])$
.
$K_0(\mathbb Z_p[G],\mathbb C_p[G])$
.
Remark 3·1. For an abelian group G and a field E with
![]() ${\mathbb{Q}_p} \subseteq E \subseteq {\mathbb{C}_p}$
the relative algebraic K-group
${\mathbb{Q}_p} \subseteq E \subseteq {\mathbb{C}_p}$
the relative algebraic K-group
![]() $K_0(\mathbb Z_p[G],E[G])$
is naturally isomorphic to
$K_0(\mathbb Z_p[G],E[G])$
is naturally isomorphic to
![]() $E[G]^\times / \mathbb{Z}_p[G]^\times$
. Moreover, these isomorphisms are induced by
$E[G]^\times / \mathbb{Z}_p[G]^\times$
. Moreover, these isomorphisms are induced by
![]() $\delta_{G,p}$
.
$\delta_{G,p}$
.
The first key step is to explicitly compute the second term that occurs in the definition of
![]() $\xi$
and to do this we use the canonical identifications (12) to identify the complex C with a unique element
$\xi$
and to do this we use the canonical identifications (12) to identify the complex C with a unique element
![]() $\delta_{A,F,p} = \delta_{C,r_1,r_2}$
of the Yoneda Ext-group
$\delta_{A,F,p} = \delta_{C,r_1,r_2}$
of the Yoneda Ext-group
![]() ${\rm Ext}^2_{\mathbb Z_p[G]}(A(F)_p^*,A^t(F)_p)$
.
${\rm Ext}^2_{\mathbb Z_p[G]}(A(F)_p^*,A^t(F)_p)$
.
For each pair (r,j) we define a dual element
![]() $P_{(r,j)}^*$
of
$P_{(r,j)}^*$
of
![]() $A(F)_p^*$
by setting, for any pair (s,i) and
$A(F)_p^*$
by setting, for any pair (s,i) and
![]() $\tau\in G$
,
$\tau\in G$
,
 \begin{equation}P_{(r,j)}^*(\tau P_{(s,i)})\;:\!=\;\begin{cases} 1, & \text{ if } r=s, j=i \text{ and } \tau\in J_r;\\ 0, & \text{ otherwise }. \end{cases}\end{equation}
\begin{equation}P_{(r,j)}^*(\tau P_{(s,i)})\;:\!=\;\begin{cases} 1, & \text{ if } r=s, j=i \text{ and } \tau\in J_r;\\ 0, & \text{ otherwise }. \end{cases}\end{equation}
By [Reference Bley and Macias Castillo6, Lemma 4·1] one then has
with each summand isomorphic to
![]() $\mathbb Z_p[\Gamma_r]$
. We fix a free
$\mathbb Z_p[\Gamma_r]$
. We fix a free
![]() $\mathbb Z_p[G]$
-module
$\mathbb Z_p[G]$
-module
of rank
![]() $N=\sum_r m_r$
and consider the exact sequence
$N=\sum_r m_r$
and consider the exact sequence
where we set
This sequence defines a canonical isomorphism
where
![]() $\iota_*$
denotes composition with
$\iota_*$
denotes composition with
![]() $\iota$
. Before proceeding to describe the map (15) let us note that it is bijective by the general result [Reference Hilton and Stammbach20, Theorem IV·9·1].
$\iota$
. Before proceeding to describe the map (15) let us note that it is bijective by the general result [Reference Hilton and Stammbach20, Theorem IV·9·1].
For a given
![]() $\phi\in{\textrm{End}}_{\mathbb Z_p[G]}(A^t(F)_p)$
we consider the push-out commutative diagram with exact rows
$\phi\in{\textrm{End}}_{\mathbb Z_p[G]}(A^t(F)_p)$
we consider the push-out commutative diagram with exact rows

In this diagram
![]() $X(\phi)$
is defined as the push-out of
$X(\phi)$
is defined as the push-out of
![]() $\iota$
and
$\iota$
and
![]() $\phi$
and all the unlabeled arrows are the canonical maps induced by the push-out construction. Then the pre-image of
$\phi$
and all the unlabeled arrows are the canonical maps induced by the push-out construction. Then the pre-image of
![]() $\phi$
under (15) is represented by the bottom row of this diagram.
$\phi$
under (15) is represented by the bottom row of this diagram.
Then, since C belongs to
![]() $D^{\rm perf}(\mathbb Z_p[G])$
, the results of [Reference Bley and Macias Castillo6, Lemmas 4·2 and 4·3] imply that there exists an automorphism
$D^{\rm perf}(\mathbb Z_p[G])$
, the results of [Reference Bley and Macias Castillo6, Lemmas 4·2 and 4·3] imply that there exists an automorphism
![]() $\phi$
of the
$\phi$
of the
![]() $\mathbb Z_p[G]$
-module
$\mathbb Z_p[G]$
-module
![]() $A^t(F)_p$
that represents the image of
$A^t(F)_p$
that represents the image of
![]() $\delta_{A,F,p}$
under (15) and also fixes the element
$\delta_{A,F,p}$
under (15) and also fixes the element
![]() $P^t_{(n,j)}$
for every j in
$P^t_{(n,j)}$
for every j in
![]() $[m_n]$
.
$[m_n]$
.
It follows that the exact sequence
is a representative of the extension class
![]() $\delta_{A,F,p}$
.
$\delta_{A,F,p}$
.
In particular, for any choice of
![]() $\mathbb C_p[G]$
-equivariant splittings
$\mathbb C_p[G]$
-equivariant splittings
and
of the scalar extensions of the canonical exact sequences
and
an explicit computation of the refined Euler characteristic occurring in the definition of
![]() $\xi$
implies that
$\xi$
implies that
 \begin{align} & -\chi_{G,p}(C,h_{A,F}^j)\\ =&-\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_2^{-1}\circ(h_{A,F}^j\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ((\mathbb C_p\cdot\phi)\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_1))\notag\\=&-\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_2^{-1}\circ(h_{A,F}^j\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_1\circ s^{-1}_1\circ((\mathbb C_p\cdot\phi)\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_1))\notag\\=&\,\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_1^{-1}\circ((h^{j}_{A,F})^{-1}\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_2))\notag\\& +\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_1^{-1}\circ((\mathbb C_p\cdot\phi^{-1})\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_1))\notag\\=&\,\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_1^{-1}\circ((h^{j}_{A,F})^{-1}\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_2))\notag\\& +\delta_{G,p}({\text{det}}_{\mathbb Q_p[G]}((\mathbb Q_p\cdot\phi^{-1})\oplus{\rm id}_{\mathbb Q_p\cdot{\textrm{im}}(\Theta)})) \nonumber \end{align}
\begin{align} & -\chi_{G,p}(C,h_{A,F}^j)\\ =&-\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_2^{-1}\circ(h_{A,F}^j\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ((\mathbb C_p\cdot\phi)\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_1))\notag\\=&-\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_2^{-1}\circ(h_{A,F}^j\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_1\circ s^{-1}_1\circ((\mathbb C_p\cdot\phi)\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_1))\notag\\=&\,\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_1^{-1}\circ((h^{j}_{A,F})^{-1}\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_2))\notag\\& +\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_1^{-1}\circ((\mathbb C_p\cdot\phi^{-1})\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_1))\notag\\=&\,\delta_{G,p}({\text{det}}_{\mathbb C_p[G]}(s_1^{-1}\circ((h^{j}_{A,F})^{-1}\oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_2))\notag\\& +\delta_{G,p}({\text{det}}_{\mathbb Q_p[G]}((\mathbb Q_p\cdot\phi^{-1})\oplus{\rm id}_{\mathbb Q_p\cdot{\textrm{im}}(\Theta)})) \nonumber \end{align}
In addition, specialising the explicit computation of [Reference Bley and Macias Castillo6, Proposition 4·4] to the case
![]() $\Phi={\rm id}_{A^t(F)_p}$
shows that
$\Phi={\rm id}_{A^t(F)_p}$
shows that
 \begin{equation} {\text{det}}_{\mathbb C_p[G]}(s_1^{-1}\circ( (h^{j}_{A,F})^{-1} \oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_2)= \left(\sum_{\psi\in\widehat{G}}j({\rm Reg}_{\psi}^{\rm NT}(\mathcal{P},\mathcal{P}^t)\cdot\delta_\psi)\cdot e_\psi\right)^{-1}.\end{equation}
\begin{equation} {\text{det}}_{\mathbb C_p[G]}(s_1^{-1}\circ( (h^{j}_{A,F})^{-1} \oplus{\rm id}_{\mathbb C_p\cdot{\textrm{im}}(\Theta)})\circ s_2)= \left(\sum_{\psi\in\widehat{G}}j({\rm Reg}_{\psi}^{\rm NT}(\mathcal{P},\mathcal{P}^t)\cdot\delta_\psi)\cdot e_\psi\right)^{-1}.\end{equation}
To compute the second term that occurs in the final equality of (20) we may and will fix any elements
![]() $\Lambda_{(r,j), (s,i)}$
of
$\Lambda_{(r,j), (s,i)}$
of
![]() $\mathbb Z_p[G]$
with the property that
$\mathbb Z_p[G]$
with the property that
We thus obtain an invertible matrix
with entries
![]() $\Lambda_{(r,j), (s,i)}$
in
$\Lambda_{(r,j), (s,i)}$
in
![]() $\mathbb Z_p[G]$
uniquely determined modulo the kernel of the canonical projection
$\mathbb Z_p[G]$
uniquely determined modulo the kernel of the canonical projection
![]() $\rho_r\;:\;\mathbb{Z}_p[G] \to {\mathbb{Z}_p}[\Gamma_r]$
, which also has the form (8).
$\rho_r\;:\;\mathbb{Z}_p[G] \to {\mathbb{Z}_p}[\Gamma_r]$
, which also has the form (8).
Recall the definition of
![]() $\varepsilon_\psi(\Lambda)$
in (2). The chosen properties of the representative
$\varepsilon_\psi(\Lambda)$
in (2). The chosen properties of the representative
![]() $\phi$
of
$\phi$
of
![]() $\delta_{A,F,p}$
fixed above then imply that
$\delta_{A,F,p}$
fixed above then imply that
The equalities (20), (21) and (23) now combine with the definition of
![]() $\xi$
to imply that
$\xi$
to imply that
![]() $\xi=\delta_{G,p}(\mathcal{L})$
with
$\xi=\delta_{G,p}(\mathcal{L})$
with
 \begin{equation*} \mathcal{L} \;:\!=\;j_*(\mathcal L^*_{A,F/k})\cdot\left( \sum_{\psi\in\widehat{G}} j({\rm Reg}_{\psi}^{\rm NT}(\mathcal{P},\mathcal{P}^t)\cdot\delta_\psi) \cdot e_\psi\right)^{-1}\cdot \left( \sum_{\psi\in\widehat{G}}\varepsilon_\psi(\Lambda)\cdot e_\psi\right). \end{equation*}
\begin{equation*} \mathcal{L} \;:\!=\;j_*(\mathcal L^*_{A,F/k})\cdot\left( \sum_{\psi\in\widehat{G}} j({\rm Reg}_{\psi}^{\rm NT}(\mathcal{P},\mathcal{P}^t)\cdot\delta_\psi) \cdot e_\psi\right)^{-1}\cdot \left( \sum_{\psi\in\widehat{G}}\varepsilon_\psi(\Lambda)\cdot e_\psi\right). \end{equation*}
By Remark 3·1 it thus follows that
![]() $\xi$
vanishes if and only if
$\xi$
vanishes if and only if
![]() $\mathcal L$
belongs to
$\mathcal L$
belongs to
![]() $\mathbb Z_p[G]^\times$
and hence the proof of Theorem 2·1 is completed by the proposition below.
$\mathbb Z_p[G]^\times$
and hence the proof of Theorem 2·1 is completed by the proposition below.
Proposition 3·2. For any
![]() $0\leq r,s\leq n-1$
we set
$0\leq r,s\leq n-1$
we set
![]() $\ell\;:\!=\;{\rm max}(r,s)$
. Then for any
$\ell\;:\!=\;{\rm max}(r,s)$
. Then for any
![]() $j\in[m_r]$
, any
$j\in[m_r]$
, any
![]() $i\in[m_s]$
and any elements
$i\in[m_s]$
and any elements
![]() $\Lambda_{(r,j),(s,i)}$
of
$\Lambda_{(r,j),(s,i)}$
of
![]() $\mathbb Z_p[G]$
satisfying (22) one has
$\mathbb Z_p[G]$
satisfying (22) one has
in
![]() $\mathbb Z_p[\Gamma_r]\otimes_{\mathbb Z_p}I_p(J_\ell)/I_p(J_\ell)^2$
.
$\mathbb Z_p[\Gamma_r]\otimes_{\mathbb Z_p}I_p(J_\ell)/I_p(J_\ell)^2$
.
Proof. We refer the reader to [Reference Burns and Macias Castillo10, Appendix B·2] for the construction of algebraic height pairings via Bockstein homomorphisms. It is proved in [Reference Burns and Macias Castillo10, Theorem 8·3] that
coincides with the inverse of the pairing induced by
where the first arrow is the Bockstein homomorphism associated to the complex of
![]() $\mathbb Z_p[J_\ell]$
-modules
$\mathbb Z_p[J_\ell]$
-modules
![]() ${\rm SC}_p(A_{F/F_\ell})$
together with the canonical identifications (12), and the second arrow is induced by restriction to
${\rm SC}_p(A_{F/F_\ell})$
together with the canonical identifications (12), and the second arrow is induced by restriction to
![]() $A(F_\ell)_p$
.
$A(F_\ell)_p$
.
Now, it is immediately clear from their definitions in [Reference Burns and Macias Castillo10, Definition 2·3] that the complexes
![]() ${\rm SC}_p(A_{F/F_\ell})$
and
${\rm SC}_p(A_{F/F_\ell})$
and
![]() ${\rm SC}_p(A_{F/k})$
are canonically isomorphic in
${\rm SC}_p(A_{F/k})$
are canonically isomorphic in
![]() $D(\mathbb Z_p[J_\ell])$
and furthermore that this isomorphism is compatible with the identifications (12). The complex
$D(\mathbb Z_p[J_\ell])$
and furthermore that this isomorphism is compatible with the identifications (12). The complex
![]() ${\rm SC}_p(A_{F/F_\ell})$
may therefore be represented by the (restriction of scalars of) the exact sequence (17).
${\rm SC}_p(A_{F/F_\ell})$
may therefore be represented by the (restriction of scalars of) the exact sequence (17).
Now
![]() $\beta_{{A,F/F_\ell,p}}$
may be computed, through the representative (17), as the connecting homomorphism which arises when applying the snake lemma to the following commutative diagram (in which both rows and the third column are exact and the first column is a complex)
$\beta_{{A,F/F_\ell,p}}$
may be computed, through the representative (17), as the connecting homomorphism which arises when applying the snake lemma to the following commutative diagram (in which both rows and the third column are exact and the first column is a complex)

From (22) and the definition of
![]() $\iota$
we immediately derive
$\iota$
we immediately derive
 \begin{equation*} \iota(\phi^{-1}(P^t_{(s,i)})) =\iota\left(\sum_{(u,h)} \Lambda_{(u,h),(s,i)} P^t_{(u,h)}\right) =\sum_{(u,h)} \Lambda_{(u,h),(s,i)} {\textrm{Tr}}_{J_u}(b_{(u,h)}).\end{equation*}
\begin{equation*} \iota(\phi^{-1}(P^t_{(s,i)})) =\iota\left(\sum_{(u,h)} \Lambda_{(u,h),(s,i)} P^t_{(u,h)}\right) =\sum_{(u,h)} \Lambda_{(u,h),(s,i)} {\textrm{Tr}}_{J_u}(b_{(u,h)}).\end{equation*}
By its definition in (13) one has
![]() $P^*_{(u,h)}(\gamma P_{(r,j)})=0$
whenever the pair (u,h) is different from (r,j). We thus find for any
$P^*_{(u,h)}(\gamma P_{(r,j)})=0$
whenever the pair (u,h) is different from (r,j). We thus find for any
![]() $\gamma\in\Gamma_r$
that
$\gamma\in\Gamma_r$
that
 \begin{align*} -\langle P^t_{(s,i)},\gamma P_{(r,j)}\rangle_{F/F_\ell}^{\rm MT}=&\left(({\rm id}\otimes_{\mathbb Z_p[J_\ell]}\pi)_{J_\ell}\left(\Theta\left({\textrm{Tr}}_{J_r/J_\ell}(\Lambda_{(r,j),(s,i)} b_{(r,j)})\right)\right)\right)(\gamma P_{(r,j)})\\[5pt] =&\left(({\rm id}\otimes_{\mathbb Z_p[J_\ell]}\pi)_{J_\ell}\left((\sigma^{p^r}-1){\textrm{Tr}}_{J_r/J_\ell}(\Lambda_{(r,j),(s,i)} b_{(r,j)})\right)\right)(\gamma P_{(r,j)})\\[5pt] =&\left(({\rm id}\otimes_{\mathbb Z_p[J_\ell]}\pi)_{J_\ell}\left((\sigma^{p^\ell}-1)(\Lambda_{(r,j),(s,i)} b_{(r,j)})\right)\right)(\gamma P_{(r,j)})\\[5pt] =&\left(\left((\sigma^{p^\ell}-1)+I_p(J_\ell)^2\right)\otimes (\Lambda_{(r,j),(s,i)}P^*_{(r,j)})\right)(\gamma P_{(r,j)})\\[5pt] =&(\sigma^{p^\ell}-1) ((\Lambda_{(r,j),(s,i)}P^*_{(r,j)})(\gamma P_{(r,j)}))+I_p(J_\ell)^2.\end{align*}
\begin{align*} -\langle P^t_{(s,i)},\gamma P_{(r,j)}\rangle_{F/F_\ell}^{\rm MT}=&\left(({\rm id}\otimes_{\mathbb Z_p[J_\ell]}\pi)_{J_\ell}\left(\Theta\left({\textrm{Tr}}_{J_r/J_\ell}(\Lambda_{(r,j),(s,i)} b_{(r,j)})\right)\right)\right)(\gamma P_{(r,j)})\\[5pt] =&\left(({\rm id}\otimes_{\mathbb Z_p[J_\ell]}\pi)_{J_\ell}\left((\sigma^{p^r}-1){\textrm{Tr}}_{J_r/J_\ell}(\Lambda_{(r,j),(s,i)} b_{(r,j)})\right)\right)(\gamma P_{(r,j)})\\[5pt] =&\left(({\rm id}\otimes_{\mathbb Z_p[J_\ell]}\pi)_{J_\ell}\left((\sigma^{p^\ell}-1)(\Lambda_{(r,j),(s,i)} b_{(r,j)})\right)\right)(\gamma P_{(r,j)})\\[5pt] =&\left(\left((\sigma^{p^\ell}-1)+I_p(J_\ell)^2\right)\otimes (\Lambda_{(r,j),(s,i)}P^*_{(r,j)})\right)(\gamma P_{(r,j)})\\[5pt] =&(\sigma^{p^\ell}-1) ((\Lambda_{(r,j),(s,i)}P^*_{(r,j)})(\gamma P_{(r,j)}))+I_p(J_\ell)^2.\end{align*}
Here the first equality uses the fact that
Now, if we write
![]() $\rho_r(\Lambda_{(r,j),(s,i)}) = \sum_{\gamma\in \Gamma_r} a_\gamma\gamma$
in
$\rho_r(\Lambda_{(r,j),(s,i)}) = \sum_{\gamma\in \Gamma_r} a_\gamma\gamma$
in
![]() $\mathbb Z_p[\Gamma_r]$
, then the definition (13) of
$\mathbb Z_p[\Gamma_r]$
, then the definition (13) of
![]() $P^*$
implies
$P^*$
implies
It therefore follows that the right-hand side of the claimed equality is equal to
as required.
For the proof that all of our constructions are independent of any choices we made we will need the following general result which is straightforward to prove.
Lemma 3·3. For any indices
![]() $0\leq r\leq\ell\leq n$
and any elements
$0\leq r\leq\ell\leq n$
and any elements
![]() $\lambda$
and
$\lambda$
and
![]() $\lambda'$
of
$\lambda'$
of
![]() $\mathbb Z_p[G]$
, one has that
$\mathbb Z_p[G]$
, one has that
in
![]() $\mathbb Z_p[\Gamma_r]\otimes_{\mathbb Z_p}I_p(J_\ell)/I_p(J_\ell)^2$
if and only if
$\mathbb Z_p[\Gamma_r]\otimes_{\mathbb Z_p}I_p(J_\ell)/I_p(J_\ell)^2$
if and only if
![]() $p^{\ell-r}(\lambda- \lambda')$
belongs to the ideal
$p^{\ell-r}(\lambda- \lambda')$
belongs to the ideal
of
![]() $\mathbb Z_p[G]$
.
$\mathbb Z_p[G]$
.
We finally justify that all assertions in the statement of our main result were indeed well-defined.
Lemma 3·4. For any elements
![]() $\Psi_{(r,j),(s,i)}$
of
$\Psi_{(r,j),(s,i)}$
of
![]() $\mathbb Z_p[G]$
satisfying the equalities (6), the sum (9) belongs to
$\mathbb Z_p[G]$
satisfying the equalities (6), the sum (9) belongs to
![]() $\mathbb C_p[G]^\times$
and is independent, up to multiplication by an element of
$\mathbb C_p[G]^\times$
and is independent, up to multiplication by an element of
![]() $\mathbb Z_p[G]^\times$
, of the choices made.
$\mathbb Z_p[G]^\times$
, of the choices made.
Proof. By Proposition 3·2, any collection of elements
![]() $-\Lambda_{(r,j),(s,i)}$
(for
$-\Lambda_{(r,j),(s,i)}$
(for
![]() $r,s<n$
) satisfying (22) also constitutes an appropriate choice satisfying the equalities (6). In addition, the sum
$r,s<n$
) satisfying (22) also constitutes an appropriate choice satisfying the equalities (6). In addition, the sum
clearly belongs to
![]() $\mathbb C_p[G]^\times$
. (In fact, by the argument of [Reference Bley and Macias Castillo6, Lemma 4·8], it also belongs to
$\mathbb C_p[G]^\times$
. (In fact, by the argument of [Reference Bley and Macias Castillo6, Lemma 4·8], it also belongs to
![]() $\mathcal{M}^\times$
, where
$\mathcal{M}^\times$
, where
![]() $\mathcal{M}$
denotes the (unique) maximal
$\mathcal{M}$
denotes the (unique) maximal
![]() ${\mathbb{Z}_p}$
-order in
${\mathbb{Z}_p}$
-order in
![]() $\mathbb Q_p[G]$
.)
$\mathbb Q_p[G]$
.)
It is therefore enough to set
![]() $\Psi'\;:\!=\;-\Lambda$
, fix any collection of elements
$\Psi'\;:\!=\;-\Lambda$
, fix any collection of elements
![]() $\Psi_{(r,j),(s,i)}$
satisfying the equalities (6), and prove that the sum
$\Psi_{(r,j),(s,i)}$
satisfying the equalities (6), and prove that the sum
 \begin{equation*}\sum_{\psi\in\widehat G}\frac{\varepsilon_\psi(\Psi)}{\varepsilon_\psi(\Psi')}\cdot e_\psi\end{equation*}
\begin{equation*}\sum_{\psi\in\widehat G}\frac{\varepsilon_\psi(\Psi)}{\varepsilon_\psi(\Psi')}\cdot e_\psi\end{equation*}
belongs to
![]() $\mathbb Z_p[G]^\times$
.
$\mathbb Z_p[G]^\times$
.
The main step involved in proving this assertion is given by the following intermediate result.
Lemma 3·5. The endomorphism
![]() $\psi$
of
$\psi$
of
![]() $A^t(F)_p$
which maps a point
$A^t(F)_p$
which maps a point
![]() $P^t_{(s,i)}$
to the sum
$P^t_{(s,i)}$
to the sum
factors through the map
![]() $\iota:A^t(F)_p\to X$
occurring in the exact sequence (14).
$\iota:A^t(F)_p\to X$
occurring in the exact sequence (14).
In addition, if we define an endomorphism
![]() $\gamma$
of
$\gamma$
of
![]() $A^t(F)_p$
by setting
$A^t(F)_p$
by setting
then
![]() $\gamma$
is bijective.
$\gamma$
is bijective.
Proof. By Lemma 3·3, for each pair (r,j),(s,i) with
![]() $r,s<n$
, there exist elements
$r,s<n$
, there exist elements
![]() $\lambda_{(r,j),(s,i)}$
and
$\lambda_{(r,j),(s,i)}$
and
![]() $\mu_{(r,j),(s,i)}$
in
$\mu_{(r,j),(s,i)}$
in
![]() $\mathbb Z_p[G]$
with the property that
$\mathbb Z_p[G]$
with the property that
 \begin{equation} \Psi_{(r,j),(s,i)}-\Psi'_{(r,j),(s,i)}=\begin{cases}(\sigma^{p^r}-1)\cdot\lambda_{(r,j),(s,i)}+{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{ if }r\geq s;\\\bigl((\sigma^{p^r}-1)\cdot\lambda_{(r,j),(s,i)}+{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\bigr)p^{r-s},\,\,\,\quad\text{ if }r< s.\end{cases}\end{equation}
\begin{equation} \Psi_{(r,j),(s,i)}-\Psi'_{(r,j),(s,i)}=\begin{cases}(\sigma^{p^r}-1)\cdot\lambda_{(r,j),(s,i)}+{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{ if }r\geq s;\\\bigl((\sigma^{p^r}-1)\cdot\lambda_{(r,j),(s,i)}+{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\bigr)p^{r-s},\,\,\,\quad\text{ if }r< s.\end{cases}\end{equation}
For
![]() $r=n$
or
$r=n$
or
![]() $s=n$
we may simply take
$s=n$
we may simply take
![]() $\lambda_{(r,j),(s,i)}$
and
$\lambda_{(r,j),(s,i)}$
and
![]() $\mu_{(r,j),(s,i)}$
to be equal to 0 and still have these equalities.
$\mu_{(r,j),(s,i)}$
to be equal to 0 and still have these equalities.
Now since
![]() $\sigma^{p^r}$
acts trivially on
$\sigma^{p^r}$
acts trivially on
![]() $P^t_{(r,j)}$
one thus has
$P^t_{(r,j)}$
one thus has
 \begin{align}\psi(P^t_{(s,i)})=&\sum_{r\geq s}{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}+\sum_{r<s}p^{r-s}{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}\notag\\=&\sum_{r\geq s}{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}+\sum_{r<s}{\textrm{Tr}}_{J_s}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}.\end{align}
\begin{align}\psi(P^t_{(s,i)})=&\sum_{r\geq s}{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}+\sum_{r<s}p^{r-s}{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}\notag\\=&\sum_{r\geq s}{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}+\sum_{r<s}{\textrm{Tr}}_{J_s}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}.\end{align}
In addition,
![]() $J_s$
acts trivially both on
$J_s$
acts trivially both on
![]() $P^t_{(s,i)}$
and on the second summand of the above expression and therefore it must also act trivially on each term
$P^t_{(s,i)}$
and on the second summand of the above expression and therefore it must also act trivially on each term
![]() ${\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}$
with
${\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}$
with
![]() $r\geq s$
. Now, since
$r\geq s$
. Now, since
![]() $\mathbb Z_p[G]\cdot P^t_{(r,j)}=\mathbb Z_p[G/J_r]\cdot P^t_{(r,j)}$
is a free
$\mathbb Z_p[G]\cdot P^t_{(r,j)}=\mathbb Z_p[G/J_r]\cdot P^t_{(r,j)}$
is a free
![]() $\mathbb Z_p[G/J_r]$
-module of rank one, this condition necessarily implies that
$\mathbb Z_p[G/J_r]$
-module of rank one, this condition necessarily implies that
![]() ${\textrm{Tr}}_{J_s/J_r}$
divides
${\textrm{Tr}}_{J_s/J_r}$
divides
![]() $\mu_{(r,j),(s,i)}$
. We may therefore, for every indices with
$\mu_{(r,j),(s,i)}$
. We may therefore, for every indices with
![]() $r\geq s$
, write
$r\geq s$
, write
![]() $\mu_{(r,j),(s,i)}={\textrm{Tr}}_{J_s/J_r}\cdot\tilde{\mu}_{(r,j),(s,i)}$
for some element
$\mu_{(r,j),(s,i)}={\textrm{Tr}}_{J_s/J_r}\cdot\tilde{\mu}_{(r,j),(s,i)}$
for some element
![]() $\tilde{\mu}_{(r,j),(s,i)}$
of
$\tilde{\mu}_{(r,j),(s,i)}$
of
![]() $\mathbb Z_p[G]$
.
$\mathbb Z_p[G]$
.
We now define a homomorphism
![]() $\alpha\;:\;X\to A^t(F)_p$
by setting
$\alpha\;:\;X\to A^t(F)_p$
by setting
and claim that
![]() $\psi=\alpha\circ\iota$
, as required to prove the first claim of the lemma.
$\psi=\alpha\circ\iota$
, as required to prove the first claim of the lemma.
Indeed, one has
 \begin{align*}(\alpha\circ\iota)(P_{(s,i)})=&\;\alpha({\textrm{Tr}}_{J_s}\cdot P_{(s,i)})={\textrm{Tr}}_{J_s}\cdot\alpha(P_{(s,i)})\\=&\sum_{r\geq s}{\textrm{Tr}}_{J_s}\cdot\tilde{\mu}_{(r,j),(s,i)}\cdot P^t_{(r,j)}+\sum_{r<s}{\textrm{Tr}}_{J_s}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}\\=&\sum_{r\geq s}{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}+\sum_{r<s}{\textrm{Tr}}_{J_s}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)},\end{align*}
\begin{align*}(\alpha\circ\iota)(P_{(s,i)})=&\;\alpha({\textrm{Tr}}_{J_s}\cdot P_{(s,i)})={\textrm{Tr}}_{J_s}\cdot\alpha(P_{(s,i)})\\=&\sum_{r\geq s}{\textrm{Tr}}_{J_s}\cdot\tilde{\mu}_{(r,j),(s,i)}\cdot P^t_{(r,j)}+\sum_{r<s}{\textrm{Tr}}_{J_s}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}\\=&\sum_{r\geq s}{\textrm{Tr}}_{J_r}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)}+\sum_{r<s}{\textrm{Tr}}_{J_s}\cdot\mu_{(r,j),(s,i)}\cdot P^t_{(r,j)},\end{align*}
which is equal to
![]() $\psi(P_{(s,i)})$
by (25).
$\psi(P_{(s,i)})$
by (25).
To prove the second claim we write
![]() $\epsilon\;:\;\mathbb Z_p[G]\to\mathbb Z_p$
for the canonical augmentation map and define a canonical ring homomorphism
$\epsilon\;:\;\mathbb Z_p[G]\to\mathbb Z_p$
for the canonical augmentation map and define a canonical ring homomorphism
![]() $\epsilon_{\mathbb F_p}$
as the composition
$\epsilon_{\mathbb F_p}$
as the composition
Now, the equalities (24) imply that
 \begin{equation*}\epsilon(\Psi'_{(r,j),(s,i)})=\begin{cases}\epsilon(\Psi_{(r,j),(s,i)})-p^{n-r}\epsilon(\mu_{(r,j),(s,i)}),\,\,\,\,\,\,\text{ if }r\geq s;\\\epsilon(\Psi_{(r,j),(s,i)})-p^{n-s}\epsilon(\mu_{(r,j),(s,i)}),\,\,\,\,\,\,\text{ if }r< s,\end{cases}\end{equation*}
\begin{equation*}\epsilon(\Psi'_{(r,j),(s,i)})=\begin{cases}\epsilon(\Psi_{(r,j),(s,i)})-p^{n-r}\epsilon(\mu_{(r,j),(s,i)}),\,\,\,\,\,\,\text{ if }r\geq s;\\\epsilon(\Psi_{(r,j),(s,i)})-p^{n-s}\epsilon(\mu_{(r,j),(s,i)}),\,\,\,\,\,\,\text{ if }r< s,\end{cases}\end{equation*}
and hence also that if
![]() $r,s<n$
then
$r,s<n$
then
![]() $\epsilon_{\mathbb F_p}(\Psi'_{(r,j),(s,i)})=\epsilon_{\mathbb F_p}(\Psi_{(r,j),(s,i)})$
(this equality is trivial for
$\epsilon_{\mathbb F_p}(\Psi'_{(r,j),(s,i)})=\epsilon_{\mathbb F_p}(\Psi_{(r,j),(s,i)})$
(this equality is trivial for
![]() $r=n$
or
$r=n$
or
![]() $s=n$
).
$s=n$
).
The ring
![]() $\mathbb Z_p[G]$
is local with maximal ideal equal to
$\mathbb Z_p[G]$
is local with maximal ideal equal to
![]() $\ker(\epsilon_{\mathbb F_p})$
. In particular an element x of
$\ker(\epsilon_{\mathbb F_p})$
. In particular an element x of
![]() $\mathbb Z_p[G]$
is a unit if and only if
$\mathbb Z_p[G]$
is a unit if and only if
![]() $\epsilon_{\mathbb F_p}(x)\neq 0$
.
$\epsilon_{\mathbb F_p}(x)\neq 0$
.
One then knows that
![]() $\epsilon_{\mathbb F_p}(\text{det}(\Psi))=\text{det}(\epsilon_{\mathbb F_p}(\Psi))=\text{det}(\epsilon_{\mathbb F_p}(\Psi'))=\epsilon_{\mathbb F_p}(\text{det}(\Psi'))\neq 0$
. It thus follows that
$\epsilon_{\mathbb F_p}(\text{det}(\Psi))=\text{det}(\epsilon_{\mathbb F_p}(\Psi))=\text{det}(\epsilon_{\mathbb F_p}(\Psi'))=\epsilon_{\mathbb F_p}(\text{det}(\Psi'))\neq 0$
. It thus follows that
![]() $\text{det}(\Psi)\in\mathbb Z_p[G]^\times$
and therefore that
$\text{det}(\Psi)\in\mathbb Z_p[G]^\times$
and therefore that
![]() $\gamma$
is bijective, as required.
$\gamma$
is bijective, as required.
Now, if we denote by [f] the pre-image in
![]() ${\rm Ext}^2_{\mathbb Z_p[G]}(A(F)_p^*,A^t(F)_p)$
under the isomorphism (15) of the class of an endomorphism f of
${\rm Ext}^2_{\mathbb Z_p[G]}(A(F)_p^*,A^t(F)_p)$
under the isomorphism (15) of the class of an endomorphism f of
![]() $A^t(F)_p$
, then Lemma 3·5 implies that
$A^t(F)_p$
, then Lemma 3·5 implies that
![]() $[\gamma]-$
$[\gamma]-$
![]() $[-\phi^{-1}]=[\psi]=0$
and hence also that
$[-\phi^{-1}]=[\psi]=0$
and hence also that
![]() $[\gamma]=[-\phi^{-1}]$
.
$[\gamma]=[-\phi^{-1}]$
.
In addition, since both
![]() $\gamma$
and
$\gamma$
and
![]() $-\phi^{-1}$
are bijective, this class in
$-\phi^{-1}$
are bijective, this class in
![]() ${\rm Ext}^2_{\mathbb Z_p[G]}(A(F)_p^*,A^t(F)_p)$
may be represented by both of the exact sequences obtained by replacing
${\rm Ext}^2_{\mathbb Z_p[G]}(A(F)_p^*,A^t(F)_p)$
may be represented by both of the exact sequences obtained by replacing
![]() $\phi^{-1}$
by
$\phi^{-1}$
by
![]() $\gamma^{-1}$
or by
$\gamma^{-1}$
or by
![]() $-\phi$
in the exact sequence (17).
$-\phi$
in the exact sequence (17).
By the general result [Reference Burns and Macias Castillo9, Lemma 4·7] there exist automorphisms
![]() $\kappa^1$
and
$\kappa^1$
and
![]() $\kappa^2$
of X with the property that the (exact) diagram
$\kappa^2$
of X with the property that the (exact) diagram

is commutative.
Now, one may compute (for instance, by the argument of [Reference Bley and Macias Castillo6, Proposition 4·4]) the desired sum as
 \begin{equation*}\sum_{\psi\in\widehat G}\frac{\varepsilon_\psi(\Psi)}{\varepsilon_\psi(\Psi')}\cdot e_\psi=\frac{{\rm det}_{\mathbb Q_p[G]}(\langle\gamma,\Theta,s_1,s_2\rangle)}{{\rm det}_{\mathbb Q_p[G]}(\langle-\phi^{-1},\Theta,s_1,s_2\rangle)}, \end{equation*}
\begin{equation*}\sum_{\psi\in\widehat G}\frac{\varepsilon_\psi(\Psi)}{\varepsilon_\psi(\Psi')}\cdot e_\psi=\frac{{\rm det}_{\mathbb Q_p[G]}(\langle\gamma,\Theta,s_1,s_2\rangle)}{{\rm det}_{\mathbb Q_p[G]}(\langle-\phi^{-1},\Theta,s_1,s_2\rangle)}, \end{equation*}
where, for any (
![]() $\mathbb Q_p[G]$
-equivariant) splittings
$\mathbb Q_p[G]$
-equivariant) splittings
![]() $s_1$
and
$s_1$
and
![]() $s_2$
as in (18) and (19), and any endomorphism
$s_2$
as in (18) and (19), and any endomorphism
![]() $\beta$
of
$\beta$
of
![]() $A^t(F)_p$
, we have written
$A^t(F)_p$
, we have written
![]() $\langle\beta,\Theta,s_1,s_2\rangle$
for the composite isomorphism
$\langle\beta,\Theta,s_1,s_2\rangle$
for the composite isomorphism
 \begin{multline*}\mathbb Q_p\cdot X\stackrel{s_1}{\to }\mathbb Q_p\cdot A^t(F)_p\oplus\mathbb Q_p\cdot{\textrm{im}}(\Theta)\stackrel{\beta\oplus{\rm id}}{\to }\mathbb Q_p\cdot A^t(F)_p\oplus\mathbb Q_p\cdot{\textrm{im}}(\Theta)\\ \to \mathbb Q_p\cdot A(F)_p^*\oplus\mathbb Q_p\cdot{\textrm{im}}(\Theta)\stackrel{s_2^{-1}}{\to }\mathbb Q_p\cdot X,\end{multline*}
\begin{multline*}\mathbb Q_p\cdot X\stackrel{s_1}{\to }\mathbb Q_p\cdot A^t(F)_p\oplus\mathbb Q_p\cdot{\textrm{im}}(\Theta)\stackrel{\beta\oplus{\rm id}}{\to }\mathbb Q_p\cdot A^t(F)_p\oplus\mathbb Q_p\cdot{\textrm{im}}(\Theta)\\ \to \mathbb Q_p\cdot A(F)_p^*\oplus\mathbb Q_p\cdot{\textrm{im}}(\Theta)\stackrel{s_2^{-1}}{\to }\mathbb Q_p\cdot X,\end{multline*}
with the unlabelled arrow simply mapping a point
![]() $P^t_{(s,i)}$
to
$P^t_{(s,i)}$
to
![]() $P^*_{(s,i)}$
.
$P^*_{(s,i)}$
.
It is then straightforward to deduce from the commutativity of the diagram (26) that
 \begin{equation*}\sum_{\psi\in\widehat G}\frac{\varepsilon_\psi(\Psi)}{\varepsilon_\psi(\Psi')}\cdot e_\psi={\rm det}_{\mathbb Z_p[G]}(\kappa_1)\cdot{\rm det}_{\mathbb Z_p[G]}(\kappa_2)^{-1}\end{equation*}
\begin{equation*}\sum_{\psi\in\widehat G}\frac{\varepsilon_\psi(\Psi)}{\varepsilon_\psi(\Psi')}\cdot e_\psi={\rm det}_{\mathbb Z_p[G]}(\kappa_1)\cdot{\rm det}_{\mathbb Z_p[G]}(\kappa_2)^{-1}\end{equation*}
and, since both of the determinants on the right hand side are by construction elements of
![]() $\mathbb Z_p[G]^\times$
, this concludes the proof of Lemma 3·4.
$\mathbb Z_p[G]^\times$
, this concludes the proof of Lemma 3·4.
4. Computation of the Mazur–Tate pairing
In this section we explain how one may numerically compute the Mazur–Tate pairing (5). The computation can be reduced to the computation of local Tate duality pairings which, in turn, may in simple situations be computed by the evaluation of Hilbert symbols thanks to recent results of Fisher and Newton [Reference Fisher and Newton18] or of Visse [Reference Visse30].
Our approach is based crucially on the ability to compute certain generalised Selmer groups, for whose calculation we will apply a method of Schaefer and Stoll [Reference Schaefer and Stoll26]. In this regard we also wish to mention subsequent work of Cremona, Fisher, O’Neil, Simon and Stoll [Reference Cremona13–Reference Cremona15] where they develop algorithms for computing n-Selmer groups by representing their elements as curves of degree n in
![]() $\mathbb{P}^{n-1}$
. However, we have not so far required using their methods.
$\mathbb{P}^{n-1}$
. However, we have not so far required using their methods.
4·1. The general strategy
We continue to assume the hypotheses of Section 2·1. In particular,as explained in Section 2·3, the result [Reference Burns and Macias Castillo10, Proposition 6·3(ii)] implies that every element of
![]() $A^t(k)_p$
and
$A^t(k)_p$
and
![]() $A(k)_p$
is ‘locally-normed’. Under this condition, Bertolini and Darmon have defined in [Reference Bertolini and Darmon1, Section 3·4·1] and [Reference Bertolini and Darmon2, Section 2·2] a pairing
$A(k)_p$
is ‘locally-normed’. Under this condition, Bertolini and Darmon have defined in [Reference Bertolini and Darmon1, Section 3·4·1] and [Reference Bertolini and Darmon2, Section 2·2] a pairing
Although the definition of this pairing is only given in the case that A is an elliptic curve, it extends naturally to our more general setting (see also [Reference Burns and Macias Castillo10,Reference Burns and Macias Castillo10]).
The results of Bertolini and Darmon in [Reference Bertolini and Darmon2, Theorem 2·8 and Remark 2·10] and of Tan in [Reference Tan29, Proposition 3·1] combine to directly show that the pairing
![]() $ \langle\ , \ \rangle_1$
coincides with the Mazur–Tate pairing
$ \langle\ , \ \rangle_1$
coincides with the Mazur–Tate pairing
![]() $\langle\ , \ \rangle_{F/k}^{\rm MT}$
. We are therefore left with the task to describe the explicit computation of
$\langle\ , \ \rangle_{F/k}^{\rm MT}$
. We are therefore left with the task to describe the explicit computation of
![]() $\langle\ , \ \rangle_1$
.
$\langle\ , \ \rangle_1$
.
Let B be either A or its dual
![]() $A^t$
. For a finite set S of non-archimedean places of k we define the generalised Selmer group
$A^t$
. For a finite set S of non-archimedean places of k we define the generalised Selmer group
to be the kernel of the localisation map
with the product running over all non-archimedean places of F that do not belong to the set S(F) of places that lie above a place in S. We recall that this group is also often referred to as a ‘relaxed Selmer group’.
By Kummer theory we then have
Here
![]() ${\textrm{res}}_w\;:\;H^1(F, B[p^n])\to H^1(F_w,B[p^n])$
denotes the canonical localisation map and
${\textrm{res}}_w\;:\;H^1(F, B[p^n])\to H^1(F_w,B[p^n])$
denotes the canonical localisation map and
![]() $\delta_w\;:\;B(F_w) / p^nB(F_w)\to H^1(F_w,B[p^n])$
is the canonical Kummer map. In particular, when S is taken to be the empty set, one recovers the usual Selmer group
$\delta_w\;:\;B(F_w) / p^nB(F_w)\to H^1(F_w,B[p^n])$
is the canonical Kummer map. In particular, when S is taken to be the empty set, one recovers the usual Selmer group
![]() ${\textrm{Sel}}^{(p^n)}(B/F)$
associated with multiplication by
${\textrm{Sel}}^{(p^n)}(B/F)$
associated with multiplication by
![]() $p^n$
.
$p^n$
.
In the following we will employ the notation from [Reference Burns and Macias Castillo10, Section 10·2·1]. We set
![]() $Z \;:\!=\; {\mathbb{Z}}/p^n{\mathbb{Z}}$
and
$Z \;:\!=\; {\mathbb{Z}}/p^n{\mathbb{Z}}$
and
![]() $R \;:\!=\; Z [G]$
and define additional R-modules
$R \;:\!=\; Z [G]$
and define additional R-modules
and
In order to define
![]() $\langle\ , \ \rangle_1$
, we first recall the construction of a canonical (local duality) perfect pairing
$\langle\ , \ \rangle_1$
, we first recall the construction of a canonical (local duality) perfect pairing
If A is defined over an
![]() $\ell$
-adic field L (for some prime
$\ell$
-adic field L (for some prime
![]() $\ell$
), then we write
$\ell$
), then we write
![]() $\langle \ , \ \rangle_{L, p^n}$
for the local Tate duality pairing obtained by combining the cup product, the Weil pairing and the invariant map as follows:
$\langle \ , \ \rangle_{L, p^n}$
for the local Tate duality pairing obtained by combining the cup product, the Weil pairing and the invariant map as follows:
 \begin{eqnarray} H^1(L, A^t[p^n]) \times H^1(L, A[p^n]) &\stackrel{\cup} \longrightarrow& H^2(L, A^t[p^n] \otimes_{\mathbb{Z}_p} A[p^n]) \nonumber \\ &\longrightarrow& H^2(L, \mu_{p^n}) \nonumber\\ &\stackrel{\rm{inv_L}}\longrightarrow& {\mathbb{Q}_p}/{\mathbb{Z}_p}. \end{eqnarray}
\begin{eqnarray} H^1(L, A^t[p^n]) \times H^1(L, A[p^n]) &\stackrel{\cup} \longrightarrow& H^2(L, A^t[p^n] \otimes_{\mathbb{Z}_p} A[p^n]) \nonumber \\ &\longrightarrow& H^2(L, \mu_{p^n}) \nonumber\\ &\stackrel{\rm{inv_L}}\longrightarrow& {\mathbb{Q}_p}/{\mathbb{Z}_p}. \end{eqnarray}
Then, for
![]() $x=(x_w)_{w \in S(F)} \in H_S^1( \mathbb{A}_F, A^t[p^n])$
and
$x=(x_w)_{w \in S(F)} \in H_S^1( \mathbb{A}_F, A^t[p^n])$
and
![]() $y=(y_w)_{w\in S(F)} \in H_S^1( \mathbb{A}_F, A[p^n])$
we set
$y=(y_w)_{w\in S(F)} \in H_S^1( \mathbb{A}_F, A[p^n])$
we set
All values
![]() $\langle x, y \rangle_{S}$
in fact belong to
$\langle x, y \rangle_{S}$
in fact belong to
![]() $\frac{1}{p^n} {\mathbb{Z}_p}/{\mathbb{Z}_p}$
, which we henceforth identify with
$\frac{1}{p^n} {\mathbb{Z}_p}/{\mathbb{Z}_p}$
, which we henceforth identify with
![]() $Z = {\mathbb{Z}} / p^n{\mathbb{Z}}$
. We may thus define the pairing (27) by the explicit formula
$Z = {\mathbb{Z}} / p^n{\mathbb{Z}}$
. We may thus define the pairing (27) by the explicit formula
We now recall the explicit definition of
![]() $\langle P, Q \rangle_1$
for
$\langle P, Q \rangle_1$
for
![]() $P \in A^t(k)$
and
$P \in A^t(k)$
and
![]() $Q \in A(k)$
. Let
$Q \in A(k)$
. Let
![]() $\Sigma$
be an admissible set of primes as in [Reference Bertolini and Darmon1, Definition 2·22], [Reference Bertolini and Darmon2, Definition 1·5] or [Reference Burns and Macias Castillo10, Lemma 10·5]. A crucial consequence of the definition of admissibility is that the canonical (diagonal) localisation map
$\Sigma$
be an admissible set of primes as in [Reference Bertolini and Darmon1, Definition 2·22], [Reference Bertolini and Darmon2, Definition 1·5] or [Reference Burns and Macias Castillo10, Lemma 10·5]. A crucial consequence of the definition of admissibility is that the canonical (diagonal) localisation map
is injective.
We write
![]() $\delta$
for the canonical global Kummer map and let
$\delta$
for the canonical global Kummer map and let
![]() $\tilde x \in {\textrm{Sel}}_\Sigma^{(p^n)}(A^t/F)^G$
denote the image of P under the canonical composition
$\tilde x \in {\textrm{Sel}}_\Sigma^{(p^n)}(A^t/F)^G$
denote the image of P under the canonical composition
We also let
![]() $\tilde y \in (A_\Sigma(\mathbb{A}_F) / p^n)^G $
be the image of Q under the canonical (diagonal) localisation map
$\tilde y \in (A_\Sigma(\mathbb{A}_F) / p^n)^G $
be the image of Q under the canonical (diagonal) localisation map
By [Reference Bertolini and Darmon1, Section 3·1] the R-modules
![]() ${\textrm{Sel}}_\Sigma^{(p^n)}(A^t/F)$
and
${\textrm{Sel}}_\Sigma^{(p^n)}(A^t/F)$
and
![]() $A_\Sigma(\mathbb{A}_F) / p^n$
are G-cohomologically trivial. We therefore find elements
$A_\Sigma(\mathbb{A}_F) / p^n$
are G-cohomologically trivial. We therefore find elements
![]() $x \in {\textrm{Sel}}_\Sigma^{(p^n)}(A^t/F)$
and
$x \in {\textrm{Sel}}_\Sigma^{(p^n)}(A^t/F)$
and
![]() $y=(y_w)_{w \in \Sigma(F)} \in A_\Sigma(\mathbb{A}_F) / p^n$
such that
$y=(y_w)_{w \in \Sigma(F)} \in A_\Sigma(\mathbb{A}_F) / p^n$
such that
We next consider the canonical (diagonal) localisation map
and the product of local Kummer maps
Then, by the definition of
![]() $\langle \ , \ \rangle_1$
given in [Reference Bertolini and Darmon2, Section 2·2], we obtain
$\langle \ , \ \rangle_1$
given in [Reference Bertolini and Darmon2, Section 2·2], we obtain
with
![]() $\langle\ , \ \rangle$
as in (27). Noting the sign involved in the definition (10) of the equivariant regulator, we are in fact interested in computing the inverse
$\langle\ , \ \rangle$
as in (27). Noting the sign involved in the definition (10) of the equivariant regulator, we are in fact interested in computing the inverse
![]() $-\langle P, Q \rangle_1$
. From the definition (29) of
$-\langle P, Q \rangle_1$
. From the definition (29) of
![]() $\langle\ , \ \rangle$
, we easily derive the explicit expression
$\langle\ , \ \rangle$
, we easily derive the explicit expression
 \begin{equation} -\langle P, Q \rangle_1 \equiv \sum_{g \in G} \left( \sum_{w \in \Sigma(F)} \langle {\textrm{res}}_w(x^g), \delta_w(y_w) \rangle_{F_w,p^n} \right) g^{} \pmod{I_p(G)^2},\end{equation}
\begin{equation} -\langle P, Q \rangle_1 \equiv \sum_{g \in G} \left( \sum_{w \in \Sigma(F)} \langle {\textrm{res}}_w(x^g), \delta_w(y_w) \rangle_{F_w,p^n} \right) g^{} \pmod{I_p(G)^2},\end{equation}
which is convenient for the explicit evaluations which we will describe in the next subsection.
4·2. Algorithmic evaluation of the pairing
In this subsection we describe how we numerically evaluate the right hand side of (31). From an algorithmic point of view we are mainly interested in the case of elliptic curves and, for this reason, we henceforth assume that
![]() $E \;:\!=\; A = A^t$
is an elliptic curve defined over k. Furthermore, we assume that
$E \;:\!=\; A = A^t$
is an elliptic curve defined over k. Furthermore, we assume that
![]() $F/k$
is cyclic of degree p where as before p is an odd prime such that E,
$F/k$
is cyclic of degree p where as before p is an odd prime such that E,
![]() $F/k$
and p satisfy the hypotheses of Section 2·1.
$F/k$
and p satisfy the hypotheses of Section 2·1.
The central computational problem in the numerical evaluation of the Mazur–Tate pairing, using the approach of Bertolini and Darmon as described in the previous section, is first of all the computation of the generalised Selmer group
![]() ${\textrm{Sel}}^{(p)}_\Sigma(E/F)$
. We will closely follow the method of Schaefer and Stoll [Reference Schaefer and Stoll26] to compute this group.
${\textrm{Sel}}^{(p)}_\Sigma(E/F)$
. We will closely follow the method of Schaefer and Stoll [Reference Schaefer and Stoll26] to compute this group.
We fix a finite set V of places of F containing the p-adic places and all places w such that the Tamagawa number
![]() $c_w$
of E at w is divisible by p. We also fix an admisible set
$c_w$
of E at w is divisible by p. We also fix an admisible set
![]() $\Sigma$
of places of k as in Section 4.1. We then write
$\Sigma$
of places of k as in Section 4.1. We then write
![]() $H^1(F, E[p]; V\cup \Sigma(F))$
for the group of cohomology classes in
$H^1(F, E[p]; V\cup \Sigma(F))$
for the group of cohomology classes in
![]() $H^1(F, E[p])$
that are unramified outside
$H^1(F, E[p])$
that are unramified outside
![]() $V \cup \Sigma(F) $
. Now the result of [Reference Schaefer and Stoll26, Proposition 3·2] shows that
$V \cup \Sigma(F) $
. Now the result of [Reference Schaefer and Stoll26, Proposition 3·2] shows that
![]() ${\textrm{Sel}}^{(p)}(E/F)$
is given by
${\textrm{Sel}}^{(p)}(E/F)$
is given by
whereas a slight generalization of the above mentioned result implies that the generalised Selmer group
![]() ${\textrm{Sel}}_\Sigma^{(p)}(E/F)$
is equal to
${\textrm{Sel}}_\Sigma^{(p)}(E/F)$
is equal to
We fix an algebraic closure
![]() $F^c$
of F and let
$F^c$
of F and let
![]() $W \subseteq E[p] \setminus \{0\}$
be a
$W \subseteq E[p] \setminus \{0\}$
be a
![]() $G_F$
-invariant spanning set for E[p]. Thus W is a union of
$G_F$
-invariant spanning set for E[p]. Thus W is a union of
![]() $G_F$
-orbits containing an
$G_F$
-orbits containing an
![]() ${\mathbb{F}_p}$
-basis of E[p]. Note that in the generic case
${\mathbb{F}_p}$
-basis of E[p]. Note that in the generic case
![]() $G_F$
acts transitively on
$G_F$
acts transitively on
![]() $E[p] \setminus \{0\}$
, so that in such cases we are forced to use
$E[p] \setminus \{0\}$
, so that in such cases we are forced to use
![]() $W = E[p] \setminus \{0\}$
.
$W = E[p] \setminus \{0\}$
.
We write
![]() $A^c \;:\!=\; {\textrm{Map}}(W, F^c)$
for the set of maps from W to
$A^c \;:\!=\; {\textrm{Map}}(W, F^c)$
for the set of maps from W to
![]() $F^c$
. Then the Galois group
$F^c$
. Then the Galois group
![]() $G_F$
acts on
$G_F$
acts on
![]() $A^c$
by conjugation, i.e., for
$A^c$
by conjugation, i.e., for
![]() $\sigma \in G_F$
,
$\sigma \in G_F$
,
![]() $a \in A^c$
and
$a \in A^c$
and
![]() $P \in W$
one has
$P \in W$
one has
![]() $(\sigma a)(P) = \sigma( a(\sigma^{-1}(P)) )$
.
$(\sigma a)(P) = \sigma( a(\sigma^{-1}(P)) )$
.
We denote by
![]() $A = {\textrm{Map}}_{G_F}(W, F^c) \;:\!=\; {\textrm{Map}}(W, F^c)^{G_F}$
the set of
$A = {\textrm{Map}}_{G_F}(W, F^c) \;:\!=\; {\textrm{Map}}(W, F^c)^{G_F}$
the set of
![]() $G_F$
-invariant maps in
$G_F$
-invariant maps in
![]() $A^c$
. Then A is a finite dimensional Étale F-algebra. Explicitly, let
$A^c$
. Then A is a finite dimensional Étale F-algebra. Explicitly, let
![]() $P_1, \ldots, P_s \in W$
be a set of
$P_1, \ldots, P_s \in W$
be a set of
![]() $G_F$
-orbit representatives of W and set
$G_F$
-orbit representatives of W and set
and
![]() $L_i \;:\!=\; {(F^c)}^{H_i}$
. Then each
$L_i \;:\!=\; {(F^c)}^{H_i}$
. Then each
![]() $L_i/F$
is a finite separable field extension and we have a canonical isomorphism
$L_i/F$
is a finite separable field extension and we have a canonical isomorphism
 \begin{equation*}A \longrightarrow \prod_{i=1}^s L_i, \quad a \mapsto \left( a(P_i) \right)_{1 \le i \le s}.\end{equation*}
\begin{equation*}A \longrightarrow \prod_{i=1}^s L_i, \quad a \mapsto \left( a(P_i) \right)_{1 \le i \le s}.\end{equation*}
The Weil pairing
![]() $e_p \colon E[p] \times E[p] \longrightarrow \mu_p(F^c)$
defines a map
$e_p \colon E[p] \times E[p] \longrightarrow \mu_p(F^c)$
defines a map
This map induces a homomorphism in cohomology
which, by [Reference Schaefer and Stoll26, Prop. 4.3], is known to be injective if
![]() $p \nmid |{\textrm{Gal}}(F(E[p])/F)|$
or
$p \nmid |{\textrm{Gal}}(F(E[p])/F)|$
or
![]() $p \nmid |W|$
.
$p \nmid |W|$
.
In addition, by an immediate generalization of Hilbert’s Theorem 90, we have a Kummer isomorphism
which combined with
![]() $\bar\omega$
defines an embedding (assuming, for example, that
$\bar\omega$
defines an embedding (assuming, for example, that
![]() $p \nmid |W|$
)
$p \nmid |W|$
)
Roughly speaking, the algorithm of Schaefer and Stoll [Reference Schaefer and Stoll26], in a first step, computes
![]() $H^1(F, E[p]; V \cup \Sigma(F)) $
as a subset of
$H^1(F, E[p]; V \cup \Sigma(F)) $
as a subset of
![]() $A^\times / A^{\times p}$
via the embedding
$A^\times / A^{\times p}$
via the embedding
![]() $\kappa \circ \bar\omega$
and then, in a second step, checks the local conditions occurring in (32).
$\kappa \circ \bar\omega$
and then, in a second step, checks the local conditions occurring in (32).
To describe the first step we let
![]() $L/F$
be a finite extension. For a finite place t of L we write
$L/F$
be a finite extension. For a finite place t of L we write
![]() ${\textrm{ord}}_t \colon L^\times \longrightarrow {\mathbb{Z}}$
for the associated normalised valuation. If T is a finite set of finite places of F, we set
${\textrm{ord}}_t \colon L^\times \longrightarrow {\mathbb{Z}}$
for the associated normalised valuation. If T is a finite set of finite places of F, we set
and more generally, if
![]() $A \simeq \prod_{i=1}^s L_i$
is an étale F-algebra as above, we define
$A \simeq \prod_{i=1}^s L_i$
is an étale F-algebra as above, we define
 \begin{equation*}A(T, p) \;:\!=\; \prod_{i=1}^s L_i(T, p).\end{equation*}
\begin{equation*}A(T, p) \;:\!=\; \prod_{i=1}^s L_i(T, p).\end{equation*}
Then, using the embedding
![]() $H^1(F, E[p]) \hookrightarrow A^\times / A^{\times p}$
given by
$H^1(F, E[p]) \hookrightarrow A^\times / A^{\times p}$
given by
![]() $\kappa\circ\bar\omega$
, the result of [Reference Schaefer and Stoll26, Corollary 5·9] shows the equality
$\kappa\circ\bar\omega$
, the result of [Reference Schaefer and Stoll26, Corollary 5·9] shows the equality
The work of Schaefer and Stoll now describes how to compute the group
![]() $H^1(F, E[p]) $
inside
$H^1(F, E[p]) $
inside
![]() $A^\times / A^{\times p}$
and then, by intersecting with the finite group
$A^\times / A^{\times p}$
and then, by intersecting with the finite group
![]() $A(V \cup \Sigma(F), p)$
, we obtain
$A(V \cup \Sigma(F), p)$
, we obtain
![]() $H^1(F, E[p]; V \cup \Sigma(F))$
as a subgroup of
$H^1(F, E[p]; V \cup \Sigma(F))$
as a subgroup of
![]() $A^\times / A^{\times p}$
. For further details we refer the reader to [Reference Schaefer and Stoll26].
$A^\times / A^{\times p}$
. For further details we refer the reader to [Reference Schaefer and Stoll26].
Testing the local conditions in the second step (see again [Reference Schaefer and Stoll26] for details) we finally obtain both
![]() ${\textrm{Sel}}^{(p)}(E/F)$
and
${\textrm{Sel}}^{(p)}(E/F)$
and
![]() ${\textrm{Sel}}_\Sigma^{(p)}(E/F)$
as subgroups of
${\textrm{Sel}}_\Sigma^{(p)}(E/F)$
as subgroups of
![]() $A^\times / A^{\times p}$
, or even better, as subgroups of the finite group
$A^\times / A^{\times p}$
, or even better, as subgroups of the finite group
![]() $A(V \cup \Sigma(F), p)$
. Note, however, that the computation of
$A(V \cup \Sigma(F), p)$
. Note, however, that the computation of
![]() $A(V \cup \Sigma(F), p)$
requires the computation of ideal class groups and units in all of the fields
$A(V \cup \Sigma(F), p)$
requires the computation of ideal class groups and units in all of the fields
![]() $L_i$
,
$L_i$
,
![]() $i = 1,..,s$
.
$i = 1,..,s$
.
In this context we recall that in the generic case we have to use
![]() $W = E[p] \setminus \{0\}$
. In any such cases we will fix
$W = E[p] \setminus \{0\}$
. In any such cases we will fix
![]() $S_0 \in W$
and set
$S_0 \in W$
and set
![]() $L \;:\!=\; F(S_0)$
, so that
$L \;:\!=\; F(S_0)$
, so that
![]() $[L:F] = p^2-1$
and
$[L:F] = p^2-1$
and
![]() $A \simeq L$
.
$A \simeq L$
.
For any place w in
![]() $\Sigma(F)$
we fix an embedding
$\Sigma(F)$
we fix an embedding
![]() $\iota_w:F\to F_w$
and set
$\iota_w:F\to F_w$
and set
![]() $A_w^c \;:\!=\; F_w^c \otimes_F A$
and
$A_w^c \;:\!=\; F_w^c \otimes_F A$
and
![]() $A_w \;:\!=\; F_w \otimes_F A$
. Note that there is a canonical isomorphism
$A_w \;:\!=\; F_w \otimes_F A$
. Note that there is a canonical isomorphism
We then consider the following commutative diagram

where
![]() $\iota_{w,*}$
is induced by composition with
$\iota_{w,*}$
is induced by composition with
![]() $\iota_w$
while the maps
$\iota_w$
while the maps
![]() $\bar\omega_w$
and
$\bar\omega_w$
and
![]() $\kappa_w$
are the local analogues of (33) and (34), respectively, and
$\kappa_w$
are the local analogues of (33) and (34), respectively, and
![]() ${\textrm{res}}_w$
is the localisation map.
${\textrm{res}}_w$
is the localisation map.
The local Tate pairing
of (28) induces a pairing
![]() $\langle\ , \ \rangle_{A_w}$
on the image of
$\langle\ , \ \rangle_{A_w}$
on the image of
![]() $\kappa_w \circ \bar\omega_w$
. In what follows we will describe the computation of
$\kappa_w \circ \bar\omega_w$
. In what follows we will describe the computation of
![]() $\langle\ , \ \rangle_{A_w}$
.
$\langle\ , \ \rangle_{A_w}$
.
We write
![]() $q_{A_w}$
for the unique quadratic form such that, for all
$q_{A_w}$
for the unique quadratic form such that, for all
one has
Let
denote the Hilbert symbol. We henceforth assume that E[p] is contained in
![]() $E(F_w)$
(which is always the case for places
$E(F_w)$
(which is always the case for places
![]() $w \in \Sigma(F)$
for an admissible set
$w \in \Sigma(F)$
for an admissible set
![]() $\Sigma$
of places of k). In this particular case one can shift the problem of computing the local Tate pairing to the computation of Hilbert symbols which is easy for places w which are prime to p by [Reference Neukirch25, Chapter V, Proposition 3·4].
$\Sigma$
of places of k). In this particular case one can shift the problem of computing the local Tate pairing to the computation of Hilbert symbols which is easy for places w which are prime to p by [Reference Neukirch25, Chapter V, Proposition 3·4].
We fix generators
![]() $S, T \in E(F_w)$
of E[p]. Then
$S, T \in E(F_w)$
of E[p]. Then
![]() $e_p(T, S)$
generates
$e_p(T, S)$
generates
![]() $\mu_p$
and we define a map
$\mu_p$
and we define a map
by
![]() $\xi_{S,T}(e_p(T, S)) = 1 + p{\mathbb{Z}}$
. For
$\xi_{S,T}(e_p(T, S)) = 1 + p{\mathbb{Z}}$
. For
![]() $\bar a \in A_w^\times / A_w^{\times p}$
with
$\bar a \in A_w^\times / A_w^{\times p}$
with
![]() $a \in A_w \simeq {\textrm{Map}}_{G_w}(W, \bar F_w)$
we obtain a well defined map
$a \in A_w \simeq {\textrm{Map}}_{G_w}(W, \bar F_w)$
we obtain a well defined map
![]() $\bar a \colon W \longrightarrow F_w^\times / F_w^{\times p}$
.
$\bar a \colon W \longrightarrow F_w^\times / F_w^{\times p}$
.
Fisher and Newton in [Reference Fisher and Newton18] have given an explicit description of the local Tate pairing associated with the p-torsion of an elliptic curve in the special case
![]() $p=3$
. Their formulas have subsequently been generalised by Visse in [Reference Visse30] to any odd prime p. In particular, from [Reference Visse30, Theorems 3·7 and 3·11] we obtain, for arbitrary odd p, an equality
$p=3$
. Their formulas have subsequently been generalised by Visse in [Reference Visse30] to any odd prime p. In particular, from [Reference Visse30, Theorems 3·7 and 3·11] we obtain, for arbitrary odd p, an equality
for all
![]() $\bar a \in (\kappa_w \circ \bar\omega_w)\left( H^1(F_w, E[p]) \right)$
. As a consequence we obtain
$\bar a \in (\kappa_w \circ \bar\omega_w)\left( H^1(F_w, E[p]) \right)$
. As a consequence we obtain
 \begin{equation} \langle \bar a, \bar b \rangle_{A_w} = \xi_{S,T} \left( \frac{\{\bar a(S), \bar b(T)\}_{F_w,p}}{\{\bar a(T), \bar b(S)\}_{F_w,p}} \right).\end{equation}
\begin{equation} \langle \bar a, \bar b \rangle_{A_w} = \xi_{S,T} \left( \frac{\{\bar a(S), \bar b(T)\}_{F_w,p}}{\{\bar a(T), \bar b(S)\}_{F_w,p}} \right).\end{equation}
We are now in a position to describe the explicit computation of
![]() $-\langle P, Q \rangle_1$
using the formula in (31). Let
$-\langle P, Q \rangle_1$
using the formula in (31). Let
![]() $\tilde y$
denote the image of Q in
$\tilde y$
denote the image of Q in
![]() $E_\Sigma(\mathbb{A}_F)/p$
as in Section 4·1. Assuming that the point Q is not divisible by p ensures that
$E_\Sigma(\mathbb{A}_F)/p$
as in Section 4·1. Assuming that the point Q is not divisible by p ensures that
![]() $\tilde y \ne 0$
because of the injectivity of the map (30).
$\tilde y \ne 0$
because of the injectivity of the map (30).
For each
![]() $v \in \Sigma$
we fix a place
$v \in \Sigma$
we fix a place
![]() $\hat v$
of F lying over v. For each
$\hat v$
of F lying over v. For each
![]() $w\in\Sigma(F)$
we define
$w\in\Sigma(F)$
we define
 \begin{equation*}y_w \;:\!=\; \begin{cases} \tilde y_{\hat v}, & \text{if } w \mid v \text{ and } w = \hat v, \\ 0, & \text{ otherwise }. \end{cases}\end{equation*}
\begin{equation*}y_w \;:\!=\; \begin{cases} \tilde y_{\hat v}, & \text{if } w \mid v \text{ and } w = \hat v, \\ 0, & \text{ otherwise }. \end{cases}\end{equation*}
Since
![]() $\tilde y$
is fixed by G it is easy to see that
$\tilde y$
is fixed by G it is easy to see that
![]() $y \;:\!=\; (y_w)_{w \in \Sigma(F)} \in E_\Sigma(\mathbb{A}_F)/p$
satisfies
$y \;:\!=\; (y_w)_{w \in \Sigma(F)} \in E_\Sigma(\mathbb{A}_F)/p$
satisfies
![]() ${\textrm{Tr}}_G(y) = \tilde y$
. Hence the formula in (31) simplifies to
${\textrm{Tr}}_G(y) = \tilde y$
. Hence the formula in (31) simplifies to
 \begin{equation}-\langle P, Q \rangle_1 \equiv \sum_{g \in G}\left( \sum_{v \in \Sigma} \langle {\textrm{res}}_{\hat v}(x^g), \delta_{\hat v}(y_{\hat v}) \rangle_{F_{\hat v},p} \right) g^{}\pmod{I_p(G)^2}.\end{equation}
\begin{equation}-\langle P, Q \rangle_1 \equiv \sum_{g \in G}\left( \sum_{v \in \Sigma} \langle {\textrm{res}}_{\hat v}(x^g), \delta_{\hat v}(y_{\hat v}) \rangle_{F_{\hat v},p} \right) g^{}\pmod{I_p(G)^2}.\end{equation}
Next we explain how to compute
![]() $x \in {\textrm{Sel}}^{(p)}_\Sigma(E/F)$
with
$x \in {\textrm{Sel}}^{(p)}_\Sigma(E/F)$
with
![]() ${\textrm{Tr}}_G(x) = \tilde x$
. The generalised Selmer group
${\textrm{Tr}}_G(x) = \tilde x$
. The generalised Selmer group
![]() ${\textrm{Sel}}^{(p)}_\Sigma(E/F)$
is computed as a subgroup of
${\textrm{Sel}}^{(p)}_\Sigma(E/F)$
is computed as a subgroup of
![]() $A^\times / A^{\times p}$
which carries an action of G induced by conjugation. Explicitly, for all
$A^\times / A^{\times p}$
which carries an action of G induced by conjugation. Explicitly, for all
![]() $\sigma \in G$
,
$\sigma \in G$
,
![]() $a \in A$
and
$a \in A$
and
![]() $S \in W$
we choose an arbitrary lift
$S \in W$
we choose an arbitrary lift
![]() $\hat\sigma \in G_k$
of
$\hat\sigma \in G_k$
of
![]() $\sigma$
and set
$\sigma$
and set
As sketched in Section 4·3 below this action is explicitly computable. We can therefore compute the
![]() ${\mathbb{F}_p}$
-representation of G induced by
${\mathbb{F}_p}$
-representation of G induced by
![]() ${\textrm{Sel}}^{(p)}_\Sigma(E/F)$
and then represent
${\textrm{Sel}}^{(p)}_\Sigma(E/F)$
and then represent
![]() ${\textrm{Tr}}_G$
as a linear map
${\textrm{Tr}}_G$
as a linear map
![]() ${\textrm{Sel}}^{(p)}_\Sigma(E/F) \longrightarrow {\textrm{Sel}}^{(p)}_\Sigma(E/F)$
and thus compute a preimage x of
${\textrm{Sel}}^{(p)}_\Sigma(E/F) \longrightarrow {\textrm{Sel}}^{(p)}_\Sigma(E/F)$
and thus compute a preimage x of
![]() $\tilde x$
.
$\tilde x$
.
In the same way we can compute the elements
![]() $x^g$
occuring in (37). Note that as an element of
$x^g$
occuring in (37). Note that as an element of
![]() $A^\times / A^{\times p}$
the element
$A^\times / A^{\times p}$
the element
![]() $\tilde x$
is given by
$\tilde x$
is given by
![]() $(\kappa\circ\bar\omega\circ\delta)(P)$
. The computation of the map
$(\kappa\circ\bar\omega\circ\delta)(P)$
. The computation of the map
is quite non-trivial and explained in [Reference Schaefer27, 28, Chapter 2] and [Reference Schaefer and Stoll26, Chapter 3], as well as the computation of the local analogue
For each
![]() $v \in \Sigma$
we now compute the completion
$v \in \Sigma$
we now compute the completion
![]() $F_{\hat v}$
together with an embedding
$F_{\hat v}$
together with an embedding
![]() $\iota_v \colon F \longrightarrow F_{\hat v}$
and define
$\iota_v \colon F \longrightarrow F_{\hat v}$
and define
![]() $a_{P, g, \hat v} \;:\!=\; {\textrm{res}}_{\hat v}(x^g) = \iota_v \circ x^g$
.
$a_{P, g, \hat v} \;:\!=\; {\textrm{res}}_{\hat v}(x^g) = \iota_v \circ x^g$
.
In order to compute
![]() $\delta_{\hat v}(y_{\hat v})$
we use the commutativity of diagram (35) and define
$\delta_{\hat v}(y_{\hat v})$
we use the commutativity of diagram (35) and define
and finally obtain
4·3. Comments on the implementation
In this subsection we discuss the restrictions on our MAGMA implementation, where we must always assume that
![]() $G_F$
acts transitively on
$G_F$
acts transitively on
![]() $E[p] \setminus \{0\}$
. Hence, for the rest of this subsection, we set
$E[p] \setminus \{0\}$
. Hence, for the rest of this subsection, we set
![]() $W = E[p] \setminus \{0\}$
and fix a point
$W = E[p] \setminus \{0\}$
and fix a point
![]() $S_0 \in W$
. As before,
$S_0 \in W$
. As before,
![]() $F/k$
is a cyclic extension of degree p where p is an odd prime.
$F/k$
is a cyclic extension of degree p where p is an odd prime.
We choose
![]() $\lambda \in \mathbb{Q}$
such that the elements
$\lambda \in \mathbb{Q}$
such that the elements
are pairwise distinct. Since
![]() $G_F$
acts transitively on W the polynomial
$G_F$
acts transitively on W the polynomial
is irreducible. It is easily seen that
![]() $F(S_0) = F(w_{S_0})$
. We therefore may and will use
$F(S_0) = F(w_{S_0})$
. We therefore may and will use
![]() $L \;:\!=\; F(w_{S_0})$
.
$L \;:\!=\; F(w_{S_0})$
.
This has the following useful consequence for the computation of
![]() $a_w \;:\!=\; \iota_w \circ a$
, where a is an element of
$a_w \;:\!=\; \iota_w \circ a$
, where a is an element of
![]() $A = {\textrm{Map}}_{G_F}(W, F^c)$
and
$A = {\textrm{Map}}_{G_F}(W, F^c)$
and
![]() $\iota_w$
an embedding of F into
$\iota_w$
an embedding of F into
![]() $F_w$
. Namely, if we assume that
$F_w$
. Namely, if we assume that
![]() $a \in A$
corresponds to
$a \in A$
corresponds to
![]() $\bar h \in F[x] / (f(x))$
under the composite map
$\bar h \in F[x] / (f(x))$
under the composite map
then we have
![]() $a(S_0) = h(w_{S_0})$
. Assume further that
$a(S_0) = h(w_{S_0})$
. Assume further that
![]() $\tilde S \in E(F_w)[p]$
and let
$\tilde S \in E(F_w)[p]$
and let
![]() $S \in W$
be such that
$S \in W$
be such that
![]() $\iota_w(S) = \tilde S$
. Then a straightforward computation shows that
$\iota_w(S) = \tilde S$
. Then a straightforward computation shows that
![]() $a_w(\tilde S) = (\iota_wh)(w_{\tilde S})$
.
$a_w(\tilde S) = (\iota_wh)(w_{\tilde S})$
.
A further useful consequence is a particularly simple description of the action of G on A. Recall that
![]() $\sigma \in G$
acts on A by conjugation as in (38). If
$\sigma \in G$
acts on A by conjugation as in (38). If
![]() $\bar h \in F[x]/(f(x))$
corresponds to
$\bar h \in F[x]/(f(x))$
corresponds to
![]() $a \in A$
, then we claim that
$a \in A$
, then we claim that
![]() $\sigma a$
corresponds to
$\sigma a$
corresponds to
![]() $\overline{\sigma h}$
. Indeed, if
$\overline{\sigma h}$
. Indeed, if
![]() $\tau(S_0) = \hat\sigma^{-1}(S_0)$
with
$\tau(S_0) = \hat\sigma^{-1}(S_0)$
with
![]() $\tau \in G_F$
, then
$\tau \in G_F$
, then
In our implementation we additionally assume
![]() $k=\mathbb{Q}$
and
$k=\mathbb{Q}$
and
![]() $p=3$
. In this case explicit formulae for the computation of the generalised Selmer group based on the work of Schaefer and Stoll in [Reference Schaefer and Stoll26] are given in [Reference Geishauser19, Section 7]. These are used throughout in our implementation.
$p=3$
. In this case explicit formulae for the computation of the generalised Selmer group based on the work of Schaefer and Stoll in [Reference Schaefer and Stoll26] are given in [Reference Geishauser19, Section 7]. These are used throughout in our implementation.
We summarise the above discussion in the following remark.
Remark 4·1. Our MAGMA implementation is restricted to handle the case
![]() $k=\mathbb{Q}$
,
$k=\mathbb{Q}$
,
![]() $p=3$
and
$p=3$
and
![]() $\mathrm{rk}(E(F)) = \mathrm{rk}(E(\mathbb{Q})) = r$
with
$\mathrm{rk}(E(F)) = \mathrm{rk}(E(\mathbb{Q})) = r$
with
![]() $r > 0$
. Assuming the validity of the classical Birch and Swinnerton–Dyer conjecture for
$r > 0$
. Assuming the validity of the classical Birch and Swinnerton–Dyer conjecture for
![]() $E/F$
the implementation will check the hypotheses (a) - (i) of Section 2·1 as well as triviality of
$E/F$
the implementation will check the hypotheses (a) - (i) of Section 2·1 as well as triviality of
![]() ${\rm{III}}_p(E_F)$
and then numerically verify the rationality part of the eTNC up to the precision of the computation. We then rigorously prove the condition from Theorem 2·1 (by rewriting it in terms of congruence relations in the manner suggested in Remark 2·6).
${\rm{III}}_p(E_F)$
and then numerically verify the rationality part of the eTNC up to the precision of the computation. We then rigorously prove the condition from Theorem 2·1 (by rewriting it in terms of congruence relations in the manner suggested in Remark 2·6).
4·4. Computations
Our MAGMA implementation can be used to numerically verify the validity of the refined Birch and Swinnerton–Dyer conjecture for pairs
![]() $(E,F/k)$
where;
$(E,F/k)$
where;
-
(i)
 $k=\mathbb{Q}$
and
$k=\mathbb{Q}$
and
 $E/\mathbb{Q}$
is an elliptic curve with global minimal Weierstrass equation;
$E/\mathbb{Q}$
is an elliptic curve with global minimal Weierstrass equation; -
(ii) F is the unique subfield of degree
 $p=3$
in
$p=3$
in
 $\mathbb{Q}(\zeta_\ell)/\mathbb{Q}$
for primes
$\mathbb{Q}(\zeta_\ell)/\mathbb{Q}$
for primes
 $\ell \equiv 1 \pmod{3}$
;
$\ell \equiv 1 \pmod{3}$
; -
(iii)
 $\mathrm{rk}(E(F)) = \mathrm{rk}(E(\mathbb{Q})) = r$
for some
$\mathrm{rk}(E(F)) = \mathrm{rk}(E(\mathbb{Q})) = r$
for some
 $r > 0$
;
$r > 0$
; -
(vi) E and F satisfy the hypotheses (a) - (i) of Section 2·1.
Note that the condition
![]() $\mathrm{rk}(E(F)) = \mathrm{rk}(E(\mathbb{Q})) = r$
ensures that
$\mathrm{rk}(E(F)) = \mathrm{rk}(E(\mathbb{Q})) = r$
ensures that
![]() $E(F)_p \simeq {\mathbb{Z}}_p^r$
is not projective as a
$E(F)_p \simeq {\mathbb{Z}}_p^r$
is not projective as a
![]() $\mathbb{Z}_p[G]$
-module.
$\mathbb{Z}_p[G]$
-module.
Here is the list of examples for
![]() $r=1$
,
$r=1$
,
![]() $\ell < 50$
and conductor less than 100. We specify elliptic curves by their Cremona reference:
$\ell < 50$
and conductor less than 100. We specify elliptic curves by their Cremona reference:
-
• E is 37a1 and
 $\ell \in \{13,19\}$
;
$\ell \in \{13,19\}$
; -
• E is 43a1 and
 $\ell \in \{7,13,37\}$
;
$\ell \in \{7,13,37\}$
; -
• E is 53a1 and
 $\ell \in \{13, 19, 31,43 \}$
;
$\ell \in \{13, 19, 31,43 \}$
; -
• E is 58a1 and
 $\ell \in \{7,13,19,31,43 \}$
;
$\ell \in \{7,13,19,31,43 \}$
; -
• E is 61a1 and
 $\ell \in \{7, 13, 43 \}$
;
$\ell \in \{7, 13, 43 \}$
; -
• E is 65a2 and
 $\ell \in \{19, 37, 43 \}$
;
$\ell \in \{19, 37, 43 \}$
; -
• E is 77a1 and
 $\ell \in \{19, 37 \}$
;
$\ell \in \{19, 37 \}$
; -
• E is 79a1 and
 $\ell \in \{13, 19, 37 \}$
;
$\ell \in \{13, 19, 37 \}$
; -
• E is 82a1 and
 $\ell \in \{13, 19, 43 \}$
;
$\ell \in \{13, 19, 43 \}$
; -
• E is 82a2 and
 $\ell \in \{13, 19, 43 \}$
;
$\ell \in \{13, 19, 43 \}$
; -
• E is 83a1 and
 $\ell \in \{7, 13, 37 \}$
;
$\ell \in \{7, 13, 37 \}$
; -
• E is 88a1 and
 $\ell \in \{7,43 \}$
;
$\ell \in \{7,43 \}$
; -
• E is 89a1 and
 $\ell \in \{19, 31, 37 \}$
;
$\ell \in \{19, 31, 37 \}$
; -
• E is 91a1 and
 $\ell \in \{31 \}$
;
$\ell \in \{31 \}$
; -
• E is 389a1 and
 $\ell \in \{7,13,43 \}$
;
$\ell \in \{7,13,43 \}$
; -
• E is 433a1 and
 $\ell \in \{7, 13, 31, 37 \}$
;
$\ell \in \{7, 13, 31, 37 \}$
; -
• E is 446d1 and
 $\ell \in \{19 \}$
.
$\ell \in \{19 \}$
.
For
![]() $r=2$
,
$r=2$
,
![]() $\ell < 50$
and conductor less than 500 we computed the following examples.
$\ell < 50$
and conductor less than 500 we computed the following examples.
-
• E is 389a1 and
 $\ell \in \{7,13,43 \}$
:
$\ell \in \{7,13,43 \}$
: -
• E is 433a1 and
 $\ell \in \{7, 13, 31, 37 \}$
;
$\ell \in \{7, 13, 31, 37 \}$
; -
• E is 446d1 and
 $\ell \in \{19 \}$
;
$\ell \in \{19 \}$
;
Acknowledgements
The authors are very grateful to David Burns for many interesting discussions and much encouragement, as well as to Christian Wuthrich for his constant interest in our work and many related discussions. We also wish to thank the referee for their careful reading of the manuscript. In particular, their comments and suggestions on Section 4 significantly helped to improve the presentation of this part of the paper.
The first author wants to thank Chris Geishauser who in the context of his master thesis [Reference Geishauser19] provided many MAGMA routines used in the computation of our numerical examples.
The second author is grateful to Stefano Vigni for some pertinent discussions. He also acknowledges financial support from the Spanish Ministry of Science and Innovation, through the ‘Severo Ochoa Programme for Centres of Excellence in R&D’ [SEV-2015-0554] and [CEX-2019-000904-S] as well as through projects [MTM2016-79400-P] and [PID2019-108936GB-C21].