No CrossRef data available.
Published online by Cambridge University Press: 24 February 2022
We define a Fibonacci fraction circle to be a circle passing through an infinite number of points whose coordinates are of the form 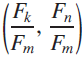 $\left( {{{{F_k}} \over {{F_m}}},{{{F_n}} \over {{F_m}}}} \right)$
, where the F’s are Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …). For instance, the circle
(1)
$\left( {{{{F_k}} \over {{F_m}}},{{{F_n}} \over {{F_m}}}} \right)$
, where the F’s are Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …). For instance, the circle
(1) $${x^2} + {\left( {y + {1 \over 2}} \right)^2} = {5 \over 4}$$
$${x^2} + {\left( {y + {1 \over 2}} \right)^2} = {5 \over 4}$$
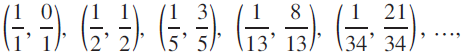 $\left( {{1 \over 1},{0 \over 1}} \right),\,\left( {{1 \over 2},{1 \over 2}} \right),\,\left( {{1 \over 5},{3 \over 5}} \right),\,\left( {{1 \over {13}},{8 \over {13}}} \right),\left( {{1 \over {34}},{{21} \over {34}}} \right),\,...,$
which can be easily checked. See Figure 1. The purpose of this paper is to find other Fibonacci fraction circles. Several of these circles have been discovered independently by Kocik. [1]
$\left( {{1 \over 1},{0 \over 1}} \right),\,\left( {{1 \over 2},{1 \over 2}} \right),\,\left( {{1 \over 5},{3 \over 5}} \right),\,\left( {{1 \over {13}},{8 \over {13}}} \right),\left( {{1 \over {34}},{{21} \over {34}}} \right),\,...,$
which can be easily checked. See Figure 1. The purpose of this paper is to find other Fibonacci fraction circles. Several of these circles have been discovered independently by Kocik. [1]