Published online by Cambridge University Press: 10 June 2004
This paper presents a model that generates a nonmonotonic evolution of the return to education. The model highlights the role played by socioeconomic stratification in the joint determination of the supply of educated labor and the supply of physical capital. The recent theoretical literature attributes the increased education premium of the last decades to skill-biased technological progress. In contrast, our explanation is based on capital–skill complementarity and endogenous accumulation of physical and human capital in an environment characterized by credit constraints.
This paper develops a theory of physical and human capital accumulation that offers an explanation for the nonmonotonic evolution of the skill premium observed in the United States and in several other western economies since the Industrial Revolution.1
The theory focuses on the role of capital–skill complementarity and socioeconomic stratification, in an environment characterized by credit constraints, in generating these nonmonotonic patterns.Most of the recent theoretical literature attributes the increased education premium of the last decades to skill-biased technological progress.2
See, among others, Galor and Tsiddon (1997), Acemoglu (1998), Caselli (1999), Galor and Moay (2000), Hassler and Rodriguez Mora (2000), Eicher and Garcia-Penalosa (2001), Gould (2001), and Gould (2002).
We extend the analysis by Krusell et al. (2000) by embedding it in a theoretical framework where the supply of production factors evolves endogenously. In particular, we introduce the assumptions that physical capital and educated labor are complements in the production process, whereas uneducated labor and physical capital are substitutes,3
In addition to Krusell et al. (2000), empirical support for the structure of the production function is presented by Griliches (1969), Katz and Murphy (1992), Krueger (1993), Baldwin and Cain (1997), and Goldin and Katz (1998).
Our explanation of the endogenous accumulation of physical and human capital highlights the role played by socioeconomic stratification in individuals' joint decisions regarding education and savings. We assume that individuals in different social groups differ in their access to education. Benabou (1996a,b) studies a variety of reasons for the stratification of access to education. Here, for simplicity, we focus on the case in which the economy is populated by groups of individuals who differ in their wealth; therefore, because of imperfections in capital markets, poorer individuals face higher costs of financing education.4
Our analysis of investment in human capital under capital market imperfections follows earlier studies by Loury (1981) and Becker and Tomes (1986), who focus on the impact of market imperfections on intergenerational mobility. Maoz and Moav (1999) extend this line of research by incorporating endogenously determined wage premium, and thereby offer an explanation for the observed relationship between income inequality, mobility, and economic growth. Here, however, in contrast to the existing literature, we offer an explanation for the nonmonotonic evolution of the education premium.
Stokey (1996), comparing growth in a closed economy with open regimes, makes the same assumptions regarding the properties of the production function as in our model. However, because of perfect capital markets and the absence of social stratification, her model does not generate nonmonotonic wage inequality dynamics.
The combination of the assumptions of capital–skill complementarity and social stratification enable an endogenous nonmonotonic evolution of the education premium. In early stages, only individuals from the rich stratum, for whom the cost of financing education is sufficiently low, purchase education. At this early phase, the increase in the supply of educated labor dominates the accumulation of physical capital and drives the education premium down. This process leads to a stage in which all of the individuals in the rich stratum acquire education, but the education premium is still not sufficiently high to encourage poorer individuals to acquire education. In this phase, the wealthy accumulate wealth by investing in physical capital. Therefore, the increase in the supply of physical capital is the dominant factor, positively affecting the demand for educated labor, negatively affecting the demand for uneducated labor and hence bringing about an increase in the education premium.6
This outline is consistent with the evidence provided by Gottschalk (1997) that much of the increase between 1979 and 1994 in the college premium in the United States stems from a 20% decline in the real wage of high school graduates. Also see Katz and Murphy (1992), Juhn et al. (1993), and Autor et al. (1998).
Consider a closed overlapping-generations economy, where economic activity extends over infinite discrete time. In every period, the economy produces a single homogeneous good that can be used for either consumption or investment. The good is produced using three production factors: physical capital, educated labor, and uneducated labor. The supply of the production factors is endogenously determined and the process of development is an outcome of the accumulation of physical and human capital.
Production occurs within a period according to a constant-returns-to-scale production technology. Consistent with conventional wisdom and recent empirical evidence, the production function is characterized by capital–skill complementarity as well as substitutability between capital and uneducated labor. The output produced at time t uses capital, Kt, uneducated labor, Ut, and educated labor, Et, in the production process:

where kt≡(Kt+Ut)/Et and α∈ (0, 1).
Producers operate in a perfectly competitive environment. Given the factor prices, producers determine the level of employment of capital, educated labor, and uneducated labor in order to maximize profits. Given the structure of the production technology and the competitiveness of markets, the wage of educated labor, wet, the wage of uneducated labor, wut, and the return to capital, Rt, at time t are

where the derivatives have the following signs:
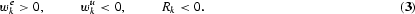
We assume that capital markets are imperfect. We model the imperfection by assuming that the interest rate for individual borrowers is higher than the interest rate for lenders, which is equal to the interest rate paid by firms. The difference between these interest rates is the real cost of keeping track of individual borrowers during their second period of life.
7We take Galor and Zeira's (1993) result of a linear cost without repeating the detailed explanation.

Our modeling of individuals' preferences and occupational choices, in an imperfect capital market environment, closely follows the framework of Galor and Zeira (1993). Individuals are identical in their preferences and their technologies of human capital formation within and across generations. They may differ, however, in their initial wealth, inherited from their parents. Thus, because of the imperfection of capital markets, their investment in human capital may differ. We assume that individuals live for two periods and have a single parent and a single child, that is, there is no population growth. When parents are in their second period of life, their children are in their first. In their first period of life, individuals who choose to become educated workers acquire an indivisible unit of education.8
We discuss the role of the indivisibility in the concluding remarks.
Individuals' preferences are defined over second-period consumption and their bequests to their children.
9 The preferences of individual j born in period t are represented by the following utility function: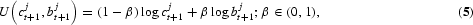
where cjt+1 is individual j's consumption in the second period of life and bjt+1 is individual j's bequest in the second period of life. Hence, it follows from the individual's maximization problem that j's bequest to the offspring is

where yjt+1 is individual j's wealth in the second period of life.
Members of generation t face an occupational choice in the first period of their life. Since individuals derive utility only from second-period consumption and bequest, maximization of second-period wealth is necessary for utility maximization. Therefore, individuals choose to become educated workers if their second-period wealth as educated workers is higher than their second-period wealth as uneducated workers.
Unless they have acquired education in the first period of life, the individuals' second-period labor unit is of the uneducated type. Education can be acquired only in the first period of life and bears a fixed cost denoted by h.10
As will become apparent, the fixed cost of education is a simplifying assumption. An alternative assumption, discussed in the concluding remarks, of indexing this cost to the skilled wage, does not have a qualitative effect on the model's results.
We now examine individual j born in period t that inherits bjt. We define this individual's wealth in t+1 by yt+1e,j if j chooses to invest in education, and by yt+1u,j if j chooses not to. It follows from (2) and (4) that
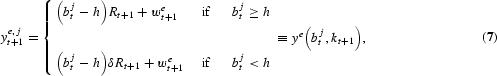
which could be represented as
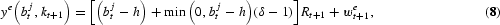
where the term min(0, bjt−h) (δ−1)Rt+1, is the additional cost for borrowing caused by the capital market imperfection.
Similarly, individual j's wealth in t+1 if he chooses not to acquire education is
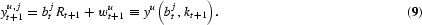
Applying (7) and (9) in the condition
for individual j to invest in human capital, we find that individual j will invest in human capital if
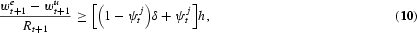
where
is the share of self-financed investment and
is the share borrowed. The right-hand side of (10) presents the investment that includes the education cost, h, and a possible finance cost. The left-hand side presents the present value of the return on the investment.
We denote the period t education premium by Pt and define it by

From (3) it follows that the left-hand side of the condition for investment in education (10) is increasing in Pt+1. Based on that, we can define individual j's critical level of education premium, denoted by
as the level of the education premium, Pt+1, for which (10) holds as an equality: if
, individual j invests in human capital, if
, individual j does not invest, and if
, individual j is indifferent whether to invest or not. Note that
is unique, positive, decreasing in bjt and increasing in h and δ. In addition, it follows from (10) that the exact values of bjt and δ are relevant for the investment decision only if bjt<h. The rationale behind these relations is that in the range bjt<h the lower the bequest received by an individual, the stronger the liquidity constraints and the incentive, in the form of an education premium, required for investment.
From (7) and (9) it follows that the second-period wealth of individual j born in period t is a function of the parental bequest, btj, and prices in t+1. Since all individuals face the same prices, it follows that all individuals who inherit a bequest of the same size in period t will have the same wealth in period t+1. Therefore, by (6), these individuals' offspring will inherit identical bequests as well, implying that the economy is characterized by a composition of strata of dynasties, where dynasty wealth, which can evolve over time, is identical within each stratum.
Suppose that in period 0 the economy consists of two groups of adult individuals who differ only in their wealth. Members of group A are a fraction λ of all adult individuals in the society. Each member of group A is endowed with a wealth level y0A. Members of group B are a fraction 1−λ of all adult individuals in the society, each endowed with a wealth level y0B, where, y0A>y0B. In every period, therefore, a fraction λ of all adults are homogeneous members of group A, and a fraction 1−λ are homogeneous members of group B.
Since wealth, yjt+1, and therefore the bequest, bjt+1, are strictly increasing functions of the transfer received by the individual, bjt, it follows that bAt>bBt and yAt>ytB for all t and therefore
for all t. Although initially the two groups are distinct, they may converge to one another. By (10), the critical values,
and
, are equal if both bAt and bBt exceed h.
Since
is decreasing in bjt, it follows that the allocation of education among the economic strata is positively correlated with wealth. In particular, if bAt>bBt and h>bBt, then the following two results hold: First, if an individual from group B acquires education, then all individuals in group A acquire education; second, if an individual from group A does not acquire education, then no individuals in group B acquire education.
Based on the definition of the critical education premium, the curve denoted by Es in Figure 1 presents the supply of educated labor and the curve denoted by ED presents the demand for educated labor in period t+1. As the economy grows, the demand curve shifts up due to the accumulation of physical capital, and the supply curve shifts down due to the relaxation of liquidity constraints as a result of the decline in the return to physical capital and the accumulation of wealth by dynasties in the economy. In periods in which demand and supply cross at the horizontal part of the supply curve, the education premium falls since the swings in demand merely provoke matching increases in the supplied quantity of Et+1. Likewise, in periods in which these curves cross at the vertical part of the supply curve, the education premium increases. This exemplifies the role of the stratification of the economy in determining which of the effects—demand or supply—will dominate the dynamics of the education premium in each period.

Demand and supply in the market for educated labor.
In our model, the stratification of the economy arises merely from wealth heterogeneity. However, as Figure 1 shows, what is actually crucial for our results is stratification of the critical education premium,
. This stratification can also arise from heterogeneity in the costs of education, h, or in the interest requirements by lenders as captured by δ.
Figure 1 also makes clear that the main results of this paper are not restricted to the simplified discrete case analyzed in this section. Consider a case in which the joint distribution of y, h, and δ is smooth but leads to a distribution of
that has peaks in it. In that case, the supply curve will be smooth, in contrast to the one in Figure 1, but it can be sufficiently elastic in certain intervals and sufficiently inelastic in others to make changes in dominance across time between the demand and supply effects on the education premium.
In this section we show that the distribution of bequests in period t, bAt and bBt, uniquely determines the equilibrium levels of human and physical capital in period t+1, Et+1, and Kt+1, and therefore uniquely determines period t+1 prices. Moreover, since prices in t+1 and the bequest bjt uniquely determine the bequest to the next generation, the initial bequest distribution (as determined by the initial wealth distribution) uniquely determines the evolution of the economy.
In each period, the economy's equilibrium is determined by the constraint on capital formation, the equality between savings and investments, and by individuals' occupational choices. Because of full depreciation of physical and human capital,

where St denotes aggregate saving in period t.
Savings are accrued by individuals in their first period of life. In the absence of first-period consumption, individuals save the bequest that they receive from their parents. Therefore, the aggregate savings in the economy is

and from (12) and (13),

Given the structure of the production technology (1), human capital is an essential factor of production, whereas physical capital can perfectly substitute for uneducated labor. Therefore, we restrict the analysis to parameter values for which Kt+1≥0 in the model's equilibrium. This implies that
.
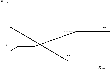
The KK line in Figure 2 describes the capital formation equation (14), which presents Kt+1 as a decreasing linear function of Et+1. Based on Figure 1, the EE line in Figure 2 shows Et+1 as a function of Kt+1 for given bAt and bBt.11
In Figure 2, the parameter values ensure that bBt<h.
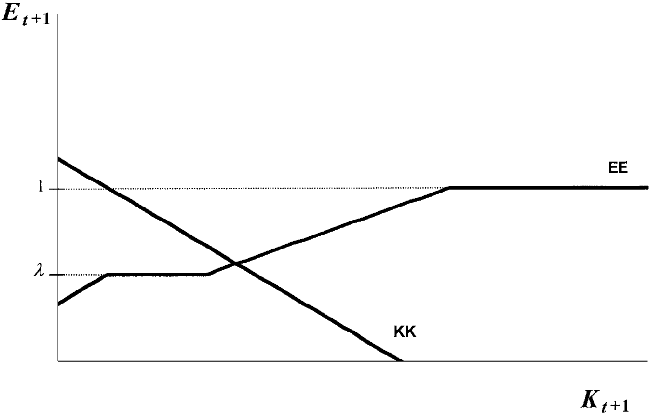
Equilibrium in the model.
Thus, since bAt and bBt determine Kt+1 and Et+1, which in turn determine bAt+1 and bBt+1, the economy can be characterized by a dynamic system of the form:

In this section we present simulations of some possible patterns for the economy's evolution. We focus on the dynamics of output, Yt, education, Et, physical capital, Kt, and the skill premium. For some parameters, the economy follows a path in which Yt, Et, and Kt monotonically increase while the skill premium monotonically declines.12
The example is based upon the following parameter values: A=10, α=0.5, β=0.3, δ=3, h=2.5, λ=0.5, bA0=2, bB0=0.
Nonmonotonic skill premium dynamics are also possible, as demonstrated by Figure 3.13
This example is based on the parameter values: A=10, α=0.5, β=0.3, δ=4, h=2.6, λ=0.35, bA0=1.98, bB0=0.
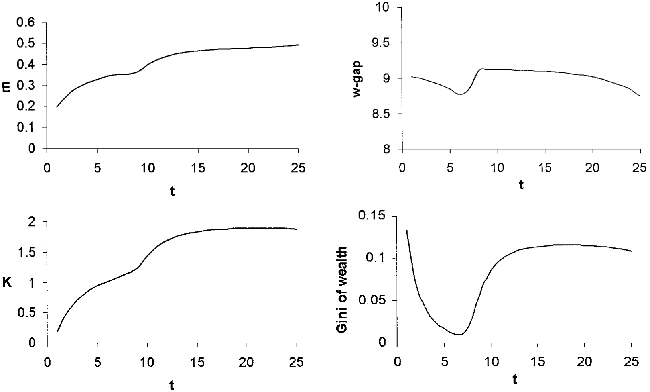
E, K, the wage gap, and the wealth Gini coefficient along the dynamic path that starts at bA=1.98 and bB=0, given A=10, β=0.3, α=0.5, h=2.5, δ=4, λA=0.35, and λB=0.65.
In this section we show that when the economy's stratification is extended beyond the case of two strata, the wage-gap dynamics may be characterized by profound cyclical behavior. To enhance the role of economic stratification, we use the following utility function:
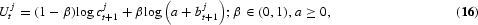
which is a generalization of the utility function used thus far. Under this utility function, the bequest function is
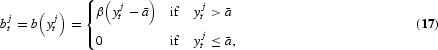
where
. Thus, the share of bequests is an increasing function of income.
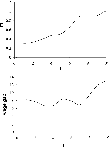
The analysis for the case of three strata (denoted A, B, C, and assuming yA0>yB0>yC0) is similar to the one performed in the previous sections for the case of two strata. Figure 4 shows the evolution of the economy, demonstrating a cyclical pattern of the skill premium.14
This example is based on the parameter values: A=10, α=0.5, h=2.5, β=0.5, a=2.7, δ=3, λA=0.5, λB=0.4, λC=0.1, yA0=2, yB0=1, yC0=0.
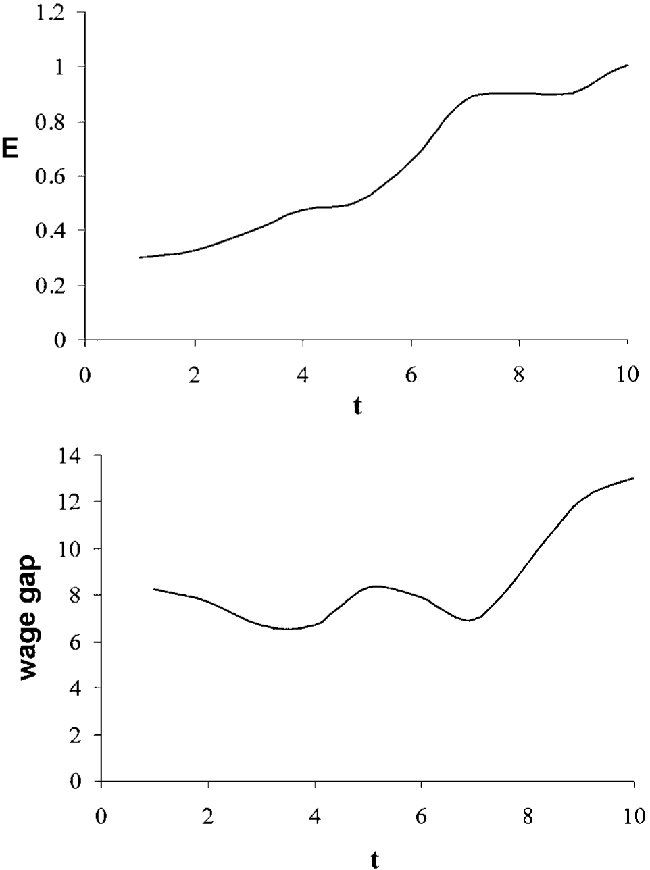
E and the wage gap along the dynamic path that starts at bA=2, bB=1, and bC=0, given A=10, α=0.5, h=2.5, β=0.5, δ=3, λA=0.5, λB=0.4, and λC=0.1.
In this paper we present a general equilibrium model, in which growth stems from physical and human capital accumulation, where skilled labor and physical capital are complementary factors in the production process, and unskilled labor and physical capital are substitutes. We show that the combination of imperfections in the capital markets and socioeconomic stratification can generate nonmonotonic skill premium dynamics.
In the model, the economy's social groups differ in their initial wealth. Because of capital market imperfections, the differences in wealth induce differences in the decisions regarding the purchase of education. Wealth differences can be replaced by stratification based on other variables, such as access to capital markets, differences in the direct cost of education, geographic location, or social barriers. As long as different strata differ in their access to education, the qualitative results of the theory should hold.
The cost of education in our model should not be viewed merely as the college tuition. For example, the social spillover discussed in several recent articles, for example, Benabou (1996a,b), may force the family to move to an appropriate neighborhood, at a large cost, in order to make higher education feasible for the offspring. Moreover, even in the absence of tuition, credit-constrained individuals may avoid higher education due to the consumption cost associated with forgone income during the time spent in school.
We take the simplifying assumption that there is only one level of education. Given the strong empirical evidence that returns to education are highest at the lowest levels of education, this assumption makes our model relevant mostly to the analysis of the decision to purchase higher levels of education.15
For such evidence on the return to education, see Psacharopoulos and Patrinos (2002).
Note that in contrast to Galor and Zeira (1993) and the related literature that focuses on poverty traps and multiple equilibria, the indivisibility of the investment in human capital is not designed to generate persistence of poverty.16
However, note that the nonconvexity of the investment technology is a crucial assumption for the persistence of wealth inequality that could emerge in the model under some parameters.
Finally, a more realistic modeling of the production of human capital would involve an indexation of the cost of education to the wage rate of skilled workers. This modification, however, would demand sacrificing simplicity. Moreover, it would have no qualitative impact on the results since the basic structure of the model, in which individuals differ only in their means of financing education, while the cost of education is identical across all individuals, is unchanged. Nevertheless, this modification can generate an interesting quantitative impact on the magnitude of changes in the education premium, and the duration of the stages of increasing or decreasing premium. A high wage of skilled workers, due to a relatively low supply of skilled workers, can further limit the access of individuals to skilled occupations, potentially increasing both the duration of periods in which the skill premium increases and the magnitude of the increase. In contrast, when the supply of skilled workers is relatively high, their wage, and therefore the cost of education, is low, further easing the access to skilled occupations, and increasing the duration of periods in which the skill premium declines and the magnitude of this decline.
We would like to thank Daron Acemoglu, Oded Galor, Joram Mayshar, Joseph Zeira, two anonymous referees, and seminar participants at the Ben-Gurion University, University of Haifa, and Hebrew University of Jerusalem for their helpful comments. We thank the Maurice Falk Institute for financial support.
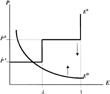
Demand and supply in the market for educated labor.
Equilibrium in the model.

E, K, the wage gap, and the wealth Gini coefficient along the dynamic path that starts at bA=1.98 and bB=0, given A=10, β=0.3, α=0.5, h=2.5, δ=4, λA=0.35, and λB=0.65.
E and the wage gap along the dynamic path that starts at bA=2, bB=1, and bC=0, given A=10, α=0.5, h=2.5, β=0.5, δ=3, λA=0.5, λB=0.4, and λC=0.1.