Published online by Cambridge University Press: 28 April 2005
In constitutional democracies, laws take time to be deliberated upon, to be passed, and to be implemented. Motivated by this observation, we study the properties of optimal tax reform when it has to be announced in advance of its implementation. We find that a delay between announcement and implementation has large effects on the optimal fiscal policy during the transition to the new steady state. On the other hand, we find that the welfare gains from optimal tax reform are fairly robust to the introduction of an implementation lag. Increasing the lag from zero to four years reduces the welfare gains by less than a quarter. Moreover, it turns out that this reduction of the welfare gain is mainly due to the delay itself rather than the effect of preannouncement on the character of the optimal tax reform.
In this paper, we study how the properties and welfare effects of optimal tax reform in a growth model are affected by a delay between announcement and implementation of the reform.
It is well known that optimal tax reform in a dynamic environment features a large initial capital levy, a large initial consumption boom, the accumulation of government assets (negative government debt), and zero taxes on capital in the long run, where the convergence to zero is immediate for a set of popular utility functions.1
In a calibrated model, Chari et al. (1994) estimate that the welfare gains from optimal tax reform correspond to an increase in consumption of about 1%.The purpose of this paper is to examine the extent to which these conclusions are affected by the introduction of a compulsory delay of T periods between announcement and implementation of an optimal tax reform.
The main source of inspiration for this exercise is the real-world experience of constitutional democracies, where laws take time to be deliberated upon, to be passed and to be implemented. This is no less true of tax laws than of other laws. According to Wilson and DiIulio (1995), a standard textbook on American government, it is especially true of tax laws: “Bills that have sped through…include ones to reduce drug abuse.…Those that have plodded through include ones dealing with…tax laws” (p. 315).
The United States is not unique in this respect. The political process leading up to the Swedish tax reform of 1991 started with a public inquiry, launched by the cabinet in 1987, and ended with an agreement between the minority Social Democratic government and the opposition Liberal party in 1990. It was applied first to income earned in 1991. Thus the whole process took about four years.
The cabinet's 1987 directive contained the basic features of the reform (broadening the tax base and lowering tax rates), and these were indeed the central features of the actual reform. The directive also stressed the importance of the committee of inquiry finishing their work in a speedy fashion. Nevertheless, it took about two years to complete the final report.2
We should perhaps stress that this paper is not about that particular reform. See Agell et al. (1995) as well as other papers in the same volume, for a discussion of that reform.
This Swedish example brings out very clearly something that is common to most major tax reforms in constitutional democracies: the basic features are known well in advance of their implementation, but the details of the legislation take time to work out and to garner majority support. On top of that, there is usually a lag between the passage of the law and when it comes into force.
Another source of inspiration can be found in Atkeson et al. (1999, p. 4). They recall the result from Chamley (1986) that “it is optimal to have an initial phase of positive capital income tax rates that is soon followed by a tax rate of zero.” They then conjecture that this property of the optimal tax reform might disappear in the presence of an implementation lag:
In practice, even if policymakers decide to move to a system of zero capital income taxes, it will take a while to actually implement the new rules. Perhaps this implementation lag corresponds roughly to the initial phase of positive capital income taxes in the model. If so, the best way to implement the Chamley result is to start the process of dispensing with capital income taxes right away (p. 4).
We interpret this passage as putting forward the conjecture that, in the presence of a sufficiently long implementation lag, it is optimal for the government to set the capital income tax to zero as soon as it is feasible to do so. This paper examines that conjecture, and we find that there does indeed exist a length of the implementation lag such that it is correct. However, this lag is very long: about 10 years. For a more reasonable length of lag, the conjecture is not true.
Our other main findings are as follows.
The remainder of the paper is organized as follows. Section 2 describes the economic environment. Section 3 discusses optimal revenue-neutral tax reform with and without preannouncement. Some of the details are relegated to Appendix A and Appendix B. Section 4 describes how the model's parameters are calibrated to fit the recent experience of the United States. Section 5 describes the numerical methods we have used. Section 6 presents the results for the benchmark case. We conclude in Section 7 by investigating the robustness of the results in the benchmark case by studying some extensions.
The economic environment is a deterministic neoclassical growth model with variable leisure and a government sector. We will denote consumption by ct, hours worked as a fraction of total available time by ht, the capital stock by kt, the real pretax interest rate by rt, the pretax wage rate by wt, the stock of government bonds by bt, and the price of government bonds by qt. In the tradition of Ramsey (1927) optimal taxation, we impose linear tax schedules, denoting the flat tax rates on labor and capital income by τth and τtk, respectively. Government spending consists of purchases gt and transfers trt.
The economy has a representative household with the period utility function U(c,h) and a competitive single production sector with the aggregate production function f(k,h).
A representative household maximizes
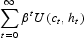
subject to
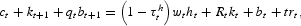
where Rt is defined via
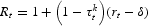
and qt is determined by the arbitrage condition
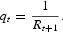
The household also faces a no. Ponzi–scheme constraint and k0 and b0 are given. Its first-order conditions with respect to labor and capital are the following:
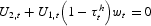
for t=0,1, …, T–1 and
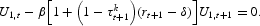
Pretax factor rental rates rt and wt are determined competitively as the marginal products of capital and labor, respectively. The economy as a whole faces the following aggregate resource constraint:
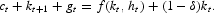
Meanwhile, by Walras's law, the government's period-by-period budget constraint is implied by the households' budget constraint and the resource constraint. The government's intertemporal budget constraint is the following:

where
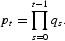
Let government spending be denoted by
where
. Similarly, let a fiscal policy be denoted by
where
, an allocation be denoted by
where
, and prices be denoted by
where
. We are now in a position to define a competitive equilibrium.
DEFINITION 1. A competitive equilibrium is a fiscal policy τ, government spending x, an allocation a, and prices π such that (i) the allocation solves the representative household's problem , given spending, policy, and prices; (ii) the resource constraint (6) is satisfied for each t=0, 1, … (iii) the government's intertemporal budget constraint (7) is satisfied; (iv) factor prices wt and rt are given by marginal products; (v) bond prices qt are given by the no-arbitrage condition (3); and (vi) bt is consistent with the household's budget constraint (2) for t = 0, 1, ….
Thus, keeping spending fixed, a competitive equilibrium maps fiscal policies into prices and allocations.
By definition, the optimal fiscal policy is that which generates (via the competitive equilibrium mapping) the allocation that is associated with the maximum value of the representative household's objective function.
A useful result in this context, proved by Lucas and Stokey (1983), is that the condition that an allocation is part of some competitive equilibrium can be summarized by the resource constraint and the following implementability condition:
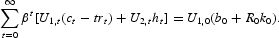
To see that any competitive equilibrium satisfies this implementability condition, take the household's intertemporal budget constraint and substitute out taxes using the household's first-order conditions (4) and (5). To see the converse, note that we can use these conditions to back out the implied tax rates that support the given allocation.
Formally, then, the Ramsey problem is to maximize

subject to (6) and (8), where k0, b0, and
are given.
Unless we impose further constraints on the problem, however, the Ramsey problem has a rather trivial solution; it is to set τ0k so high that it generates enough revenue to buy government claims on the private sector so that taxes need never be levied again.
To avoid this triviality, we assume, following Chari et al. (1994), that the initial capital income tax rate τ0k is determined exogenously. Notice that this assumption is not needed when there is an implementation lag.
Let
. Then the first-order conditions of the Ramsey problem are, for
,
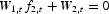
and
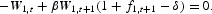
Period t=0 is special; see Appendix A.
We interpret the idea that a reform has to be announced T periods in advance in the following way. In periods t=0,1, …, T−1 (during the implementation lag), tax rates are constrained to equal their (exogenously given) historical values, denoted by
and
. That is, the Ramsey policymaker faces the following constraints:
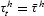
and
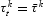
for t=0, 1, …, T−1.
We can translate these constraints on tax rates into constraints on allocations by invoking the representative agent's first-order conditions for optimal labor supply and optimal saving (4) and (5). The result is
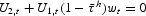
for t=0, 1, …, T−1 and
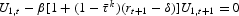
for t=0, 1, …, T−2.
The second of these constraints is of a nonstandard kind, as discussed by Marcet and Marimon (1995). As a consequence, the Lagrange multiplier
associated with the capital income tax constraint (15) becomes a state variable in the sense that its initial value is given (
) and that the value of ηt is relevant for decisions taken in period t.
When there is no implementation lag (T=0), we impose a further constraint in order to avoid an initial confiscation large enough to implement the Pareto-optimal allocation. One way of doing this would be to impose an upper limit on the initial capital income tax rate. Instead, we fix the initial capital income tax rate to its historically given value; that is,
. Thus, when
the first freely chosen capital income tax is
, and when T=0, the first freely chosen capital income tax rate is
. Regardless of the value of T, the first freely chosen labor income tax is
. The first-order conditions for this problem can be found in B.
The model is calibrated so as to fit the recent experience of the United States.
We set the labor tax rate
and the capital income tax rate
. These numbers are taken from Carey and Tchilinguirian (2000, Table 4), which are an average of the years 1991–1997. The value 0.27 for the labor tax incorporates taxes on consumption.3
There is some controversy concerning the measurement of tax rates, especially on capital. Indeed, Gordon and Slemrod (1988) claimed that the U.S. government raises no significant revenue from the federal capital income tax. This study ignored state and local taxes on capital income and property, and this is potentially an important omission; this is why we rely on other studies rather than this one. In any case, Gordon et al. (2003) assert that the U.S. government now does raise a significant amount of revenue from the federal income tax.
Government purchases gt are set constant at a level so that the steady-state ratio of government purchases to GDP generated by the model with current policy is 0.19, which is the average postwar figure for the United States. Transfer payments are also constant and are determined so as to balance the budget in the prereform steady state. This implies a prereform steady-state ratio of transfers to GDP of 0.075. This is slightly less than the U.S. postwar average, which is about 10%.
Initial government debt b0 is set to zero in the benchmark case. See Section 7 for a discussion of what happens when this assumption is modified.
The production function is defined via
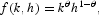
where θ =0.36 to match the postwar capital share of income in the United States.
The period utility function is defined via
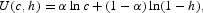
where α =0.377 so as to deliver h=0.31 in the prereform steady state. This value is taken from Cooley and Prescott (1995). The value of k0 is set so as to equal the prereform steady state.
We set the subjective annual discount factor β so as to match an annual capital output ratio of 2.9 reported by Gomme and Rupert (2003). We use the same source for the annual depreciation rate, which is set to δ = 0.064.
Each period is taken to represent two years, which we think of as the minimal time it can realistically take between a tax reform being proposed and its being implemented.
When λ, the shadow value of the implementability constraint (8) has been fixed, the Ramsey equilibrium can be characterized by a system of nonlinear equations. By assuming that the economy converges to a steady state in finitely many periods, we can make this system finite-dimensional. Having solved this system of equations, we then check whether equation (8) is satisfied. If not, we adjust λ until it is. These methods are standard and we claim no originality for them.
For the first-order conditions to characterize a local maximum, the Lagrange function should be locally concave in the decision variables. Since the Lagrange function has infinitely many terms (and involves infinitely many decision variables), we truncate it after T* terms, where T* is chosen so that βT* is very close to zero. We then evaluate the Hessian matrix of this function with respect to the decision variables in periods t=0, 1, …, T* at the point where the gradient is zero. This Hessian turns out to be negative semidefinite in all the cases we compute.
In this section, we present the properties of the solution for different values of T.
As a reference point, we begin by describing the standard case of no implementation lag (T=0) studied by Chari et al. (1994). The first row of Table 1 shows that in this case, the period 1 capital income tax is set to 299% and the period 0 labor tax to −7%. Thereafter, the capital tax is set to approximately zero, and the labor tax to 32%. As a result of the high initial capital tax, the government accumulates assets during the transition (see Figure 1). For the purposes of this paper, a tax policy is said to be frontloaded if part of government spending in the steady-state is financed by returns on assets accumulated during the transition. This phenomenon has been discussed by Jones et al. (1997, p. 116) who call it a “disturbing but essential feature of the optimal tax code.” Indeed, as Jones et al. (1993) show, there is a wide class of models in which the optimal tax code is characterized by complete frontloading in the sense that all taxes tend to zero.4
This class of models have labor services supplied jointly with human capital and constant returns in the accumulation of human and physical capital. Our benchmark model does not feature human capital accumulation and hence is not a member of this class.


Dynamics of government debt
Corresponding to the low incentives to save as a result of the very high (299%) capital income tax in period 1, there is a huge boom in consumption in period 0 (see Figure 2) and a consequent reduction of the capital stock (see Figure 3). Subsequently, consumption falls precipitously in response to the fall in the capital income tax rate. Consumption then converges from below to its new, higher steady state as capital is accumulated and consumption possibilities are extended. Hours worked, on the other hand, converge to their new steady-state value from above. This is a consequence of the low first-period labor tax.

Dynamics of consumption and hours

Dynamics of capital
Consider now what happens when the tax reform is preannounced. When T=2, the character of the solution has changed rather dramatically. The period 0 consumption boom is gone (see Figure 2), and the economy instead immediately commences its accumulation of capital toward the new steady state (see Figure 3). Indeed, consumption falls in anticipation of the future fall in the capital income tax rate. The household knows that it will eventually want to accumulate more capital. This involves cutting consumption temporarily. To smooth this fall in consumption over time, households commence the cut in consumption before the tax cut comes into effect.
Table 1 shows the optimal tax rates for different implementation lags. Note that the first freely chosen capital income tax rate falls as T increases. Indeed, it is negative for T>7, and converges to about −95% as T becomes large (see Figure 4). This gives the private sector incentives to invest heavily in the periods leading up to T−day (t=T). This speeds up convergence of the capital stock to its steady-state value, so that, at T = 10, it is almost immediate. When T increases beyond 25, the solution does not change much when T is increased further.

Capital income tax at t = T (at t = T+1 if T = 0)
Moreover, the labor tax increases almost immediately to its new steady-state value when T>0. Meanwhile, households continuously increase their labor supply during the periods
. This increase is due to the gap between prereform an postreform labor income tax rates and the accumulation of capital that raises the real pretax wage.
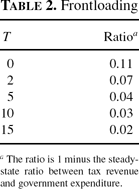
Finally, while Jones et al. (1993) may be right in saying that frontloading is an essential feature of Ramsey optimal reform, we find that the extent of frontloading depends negatively on the size of the interval between announcement and implementation of the reform. Indeed, in our setup, it is quantitatively insignificant when policy is preannounced sufficiently far in advance. As exhibited in Table 2 and Figure 1, the quantitative importance of frontloading diminishes as T increases, although it does not disappear entirely. When T=2, 7% of government expenditures are covered by returns on government assets in the steady state. When T=15, this figure is only 2%
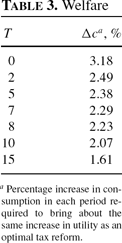
It is well known that there exist large welfare gains from pursuing an optimal tax reform involving the elimination of capital taxation [see Lucas (1990)]. In our model economy, when T = 0, the welfare gains correspond to an increase in consumption of about 3.18%. As shown in Table 3, the welfare gains diminish as the preannouncement period T increases. When T = 5, the gain is 2.38%, and when T = 15, it is 1.61%. In principle, this is not so strange. Preannouncement (unlike commitment) represents a constraint that a maximizing government would like to avoid if it could.
Decomposing the welfare gains from optimal tax reform, Chari et al. (1994) find that the majority of the welfare gains come from the very high period 1 capital income tax. They do this by considering a tax reform that sets capital income tax rates to zero in all periods from period 1 on. (This tax reform is, of course, not optimal.) When we perform a constant-tax reform experiment similar to that of Chari et al. (1994), we similarly find that almost 45% of the welfare gains from tax reform disappear.
However, a look at the welfare gains from preannounced tax reform shows that it would be wrong to conclude that a very high initial (period 1) capital income tax is necessary to obtain large welfare gains from tax reform.
When T = 5 and the first freely chosen (t = T) capital income tax rate is only about 62%, the welfare gains correspond to an increase in consumption of about 2.38%, so that only about a quarter of the welfare gains of the T = 0 case have disappeared. When T = 8 and the initial capital income tax rate is −8%, the welfare gains still correspond to an increase in consumption of about 2.23%, so that less than 30% of the gains have disappeared.
We conclude from this that an excellent alternative to setting a very high capital income tax in one period is to set it at moderate positive levels for several periods. Certainly, this is much better than reducing capital taxes to zero immediately. This result is in the spirit of Chamley (1986, Theorem 2). There, exogenous bounds are imposed on tax rates and the optimal policy is to set the capital income tax rate equal to the upper bound during an initial phase and to zero thereafter. The lower the upper bound, the longer is the initial phase.
The proposition that only a small fraction of the welfare gains from optimal tax reform is attributable to a very high period 1 capital levy receives further support from the following considerations. Our calculations of the welfare gains from optimal preannounced tax reform presented so far include the effect of mere delay as well as the effect of preannouncement on the character of the tax reform. Thus, it may be that the reduction in welfare gain as a result of preannouncement is a result of the delay as such rather than the removal of the very high period 1 capital tax rate feature. Indeed, as we shall see, that is very nearly the case.
In this section, we discuss the extent to which the reduction in welfare gain when T increases is a result of mere delay (a good thing coming later rather than sooner), as opposed to the changed character of the optimal tax reform. To investigate this issue, we look again at the allocations generated by the optimal tax reforms for different values of T. To isolate the delay effect, we evaluate these allocations according to the following objective function:
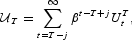
where
is the period t utility generated by the optimal tax reform announced at t = 0 and implemented in period T. With this measure, there are always exactly j prereform periods in each evaluated path, so that the mere delay effect is held constant. We set j = 8 since, as Figures 2 and 3 show, when T is large, the allocation generated by the optimal preannounced policy stays more or less at the steady-state generated by current policy until there are about eight periods left until the implementation of the reform. This means that, in each case, we are evaluating all parts of the path that are affected significantly by the reform.
Notice that this delay-compensated measure coincides with the usual one when T = 8. Notice also that for T<8, the objective function will involve periods with t<0. For these periods, we set the allocations (and hence the period utility) equal to the steady-state values generated by current tax policy.
The results can be seen in Table 4. We notice that once the tax reforms for different values of T are put on a level playing field with respect to the pure delay effect, their welfare gains are rather similar. Thus, we conclude that the welfare gains from optimal tax reform do not hinge on extreme initial tax rates or consumption booms. Indeed, the welfare gains are greatest when T = 8, when the capital accumulation is smoothest, and the initial consumption boom is gone entirely.

In this section we discuss the robustness of the results to changes in two aspects of the benchmark setup: the period length and the assumption of zero initial government debt.
Since there is full commitment, the period length does not represent the frequency with which the government can reconsider its policy. It does, however, represent the frequency with which all variables, including tax rates, can be changed, and it is not obvious that the results are robust to changes in this frequency. Nevertheless, we find that they are. In the benchmark case, the parameters β and δ are calibrated so that the period length can usefully be thought of as two years. When these parameters are changed so that each period corresponds to a single year, the results are very similar. As seen in Figures 5 and 6, the dynamics of capital and consumption are largely unchanged except possibly for initial consumption when T = 0, which is noticeably higher when the period length is shorter.5
Notice that equal distances along the horizontal axis in the figures correspond to equal numbers of years rather than equally many time periods.

Dynamics of capital for one- and two-year periods. Capital is normalized by the one-year-period steady-state level under exogenous policy.

Dynamics of consumption for one- and two-year periods. Consumption is normalized by the one-year-period steady-state level under exogenous policy
In the benchmark parameterization, we set b0=0. The results are not affected in any significant way if instead we follow Chari et al. (1994) in calibrating initial government debt to equal 51% of GDP in the steady state generated by average current policy. Figures 7 and 8 exhibit the dynamics of capital, consumption, and hours for T = 0 and T = 5, with and without positive initial debt. The main qualitative difference lies in the increased incentive to lower the value of initial private assets (since these are now larger) when T = 0. This leads to a larger initial consumption boom in this case. When policy is preannounced five periods (10 years) in advance, however, initial government debt barely matters at all for the allocations.

Dynamics of government debt, with and without initial debt

Dynamics of consumption and hours, with and without initial debt
Nevertheless, initial government debt does of course matter for the behavior of government debt itself. As displayed in Figure 9, an increase in initial debt leads essentially to a permanent upward shift in government debt by the same amount, leaving government deficits almost unchanged.

Dynamics of government debt, with and without initial debt
Finally, it is worth noting that positive initial government debt causes interest payments to crowd out transfer payments. At the given current tax rates and government consumption, transfer payments fall from about 7.5% of GDP to 4.5% when initial government debt is increased from 0 to 51% of GDP.
The period t = 0 first-order conditions for the standard Ramsey problem of Section 3.1. are
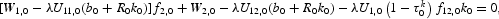
and
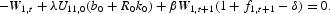
The first-order conditions for the preannounced optimal reform of Section 3.2. are as follows. For periods
, we have
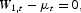
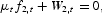
and
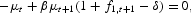
where μt is the Lagrange multiplier associated with the resource constraint (6). These equations are equivalent to (10) and (11).
For t=T−1, we have
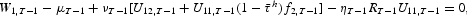
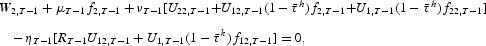
and
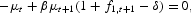
where νt is the Lagrange multiplier associated with the labor income tax constraint (14).
For t=1, 2, …, T−2, we have
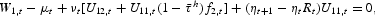
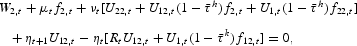
and
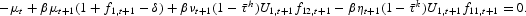
Finally, for t=0, we have
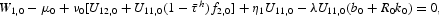
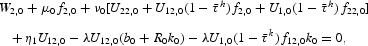
and
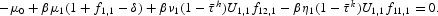
We thank Torsten Persson, Kjetil Storesletten, Harald Uhlig, Gustavo Ventura, and seminar participants at the Federal Reserve Banks of Minneapolis and Richmond for helpful comments and suggestions. Generous financial support from Tom Hedelius och Jan Wallanders stiftelse för samhällsvetenskaplig forskning and Carl Mannerfelts fond is gratefully acknowledged.

Optimal tax rates, %
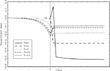
Dynamics of government debt
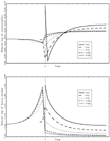
Dynamics of consumption and hours

Dynamics of capital
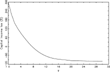
Capital income tax at t = T (at t = T+1 if T = 0)
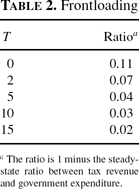
Frontloading
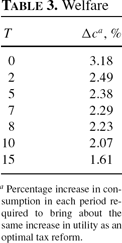
Welfare

Welfare gains with the pure delay effect held constant

Dynamics of capital for one- and two-year periods. Capital is normalized by the one-year-period steady-state level under exogenous policy.

Dynamics of consumption for one- and two-year periods. Consumption is normalized by the one-year-period steady-state level under exogenous policy

Dynamics of government debt, with and without initial debt

Dynamics of consumption and hours, with and without initial debt
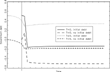
Dynamics of government debt, with and without initial debt