INTRODUCTION
This paper presents a simple theoretical model of the persistent slump in the productivity growth rate in the Japanese economy during the 1990s, during which time huge amounts of bad loans were rolled over under the government's (implicit) forbearance policy. Hayashi and Prescott (2002) show that the annual growth rate of total factor productivity (TFP) in the 1991–2000 period was 0.3%, while that in the 1983–1991 period was 3.7%. They stress that this sharp and persistent decline of TFP growth was the main cause of Japan's lost decade.1
The TFP slowdown during the 1990s is confirmed by several authors. Jorgenson and Motohashi (2003) report that Japan's TFP growth was 1.01% in the 1975–1990 period and 0.74% in the 1990–1995 period. Miyagawa (2003) reports that TFP growth was 1.63% in the 1981–1990 period and 0.84% in the 1991–1999 period. The disagreements seem mainly due to differences in the definitions of capital inputs and the TFP factor. Recently, Kawamoto (2004) has shown that the observed TFP slowdown may be a result of mismeasurements of capital and labor utilizations and the effect of resource reallocations among industries.
In this paper, I propose a purely theoretical model that may explain the decline in productivity growth. The model focuses on the payment process in the economy, in which a firm buys an intermediate input, transforms it into the next-stage intermediate good, and sells it to another firm. The intermediate goods are passed down from firm to firm in the market and are finally transformed into consumer goods. On the one hand, I postulate an assumption, which seems fairly orthodox in economics [Smith (1776); Becker and Murphy (1992)] but does not generally receive much attention in recent macroeconomic literature, that productivity is enhanced by the division of labor. That is, the greater the number of firms that process an intermediate good is, the larger the number of the final consumer goods will be. On the other, I assume that the increase of insolvent firms continuing to operate on the verge of bankruptcy makes a persistent “payment uncertainty,” that there remains a positive probability that an insolvent firm will go bankrupt and will fail to pay its suppliers. An increase in the number of firms that process one intermediate good results in an increase in productivity, which enhances the profit of a firm, while it also causes a rise in payment uncertainty, which depresses the expected profit of the firm. Thus, payment uncertainty causes an endogenous decline in productivity through firms' decision making over the division of labor.
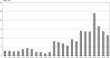
Because the rollover of bad loans was widespread in Japan after the asset-price bubbles burst in the early 1990s, this argument gives a possible explanation for the sudden decline of TFP growth in the 1990s. Figure 1 shows the liabilities of failed firms in the Japanese economy. After the speculative bubbles burst, the level of liabilities rose to about 10 trillion yen on the average in the 1990s from about 3 trillion yen in the 1980s. This increase in bankruptcies indicates that economic agents began to feel more risk of not being paid by their customers in the 1990s.

Total liabilities of failed businesses. Source: Tokyo Shoko Research. Note: Summary of major business failures with more than 10 million yen in liabilities.
According to reports by Teikoku Data Bank, a private research institute specializing in corporate bankruptcies, and the Ministry of Economy, Trade, and Industry, the average repayment ratio of general debt by bankrupt firms in the rehabilitation process was about 25% in the 1990s [Teikoku Data Bank (2001a, 2001b); Ministry of Economy, Trade, and Industry (2004a, 2004b)].2
The reports aggregate the data only for firms that filed for bankruptcy under the Corporate Rehabilitation Law and the Civil Rehabilitation Law. A significant number of bankrupt firms did not enter the rehabilitation process but were simply liquidated. Because the financial health of liquidated firms was likely to have been much worse than that of rehabilitated firms, the true repayment rate by bankrupt firms is probably much lower than 25%.
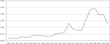
The rise in (subjective) risk for firms is also confirmed by financial statements. Data from Kigyo Zaimu Data Bank, a comprehensive data set of financial statements of listed companies constructed by the Development Bank of Japan, shows that in the 1990s there was a significant rise in bad-debt losses and transfers to reserves for bad debts. Figure 2 shows the ratio of losses and transfers to total corresponding financial assets. The rise of the ratio implies that large firms in the Japanese economy experienced an increase in payment uncertainty during the 1990s. The ratio rose from 0.4% in the late 1980s to about 1.0% in the 1994–1997 period and to 2.4% in 2000. Because this ratio must be proportional to the subjective payment uncertainty that firms experience, we may say that payment uncertainty doubled in the mid-1990s and rose nearly sixfold between the late 1980s and the late 1990s.3
To be more precise, payment uncertainty in year t must be approximated by the ratio of losses and transfers in year t to total corresponding claims that become due in year t. Because data on due dates are not available from financial statements, I use the total amount of corresponding financial assets as a proxy. Assuming that a fixed proportion of the claims becomes due every year, we may say that the ratio in the text is proportional to the subjective payment uncertainty.

Increase in payment uncertainty. Source: Kigyo Zaimu Data Bank, Development Bank of Japan. Notes: a. Code numbers of Kigyo Zaimu Data Bank are in parenthesis. b. Payment uncertainty is approximated by (bad-debt losses (K3250) + transfers to reserves for bad debts (K3630))/(notes and trade accounts receivable + other claims). c. Notes and trade accounts recievable = “notes receivable” (K0900, K0910) + “trade accounts receivable” (K0920, K0930). d. Other claims = “operating loans” (K1010) + “other quick assets” (K1020) + “suspended payments” (K1140) + “advances” (K1150) + “advances from affiliates” (K1160) + “prepaid expences” (K1170) + “accrued revenue” (K1180) + “accrued revenue from affiliates” (K1190) + “short-term loans” (K1200) + “short-term loans to affiliated companies” (K1210) + “recievables” (K1220) + “recievables from affiliates” (K1230) + “other short-term claims to affiliated companies” (K1240) + other “other current assets” (K1250) + “long-term loans” (K1630) + “long-term loans to shareholders, executives, and employees” (K1640) + “long-term loans to affiliated companies” (K1650) + “rehabilitation claims, etc.” (K1660) + “rehabilitation claims to affiliated companies” (K1670) + “long-term prepaid expenses” (K1680) + “long-term recievables” (1690) + “other long-term loans to affiliated companies” (K1710) + “other investments and other assets” (K1730).
Such circumstantial evidence of a rise of payment uncertainty may be said to support the plausibility of the scenario in this paper.
The organization of the paper is as follows. In the next section I present the basic structure of the model, in which there is no payment uncertainty. In Section 3, I introduce payment uncertainty and describe the endogenous decline of productivity under the forbearance policy of the government. In Section 4, the basic model is embedded in a standard growth model, in which the representative consumer accumulates capital stocks. The performance of the extended model is then compared with that of the Japanese economy. Section 5 discusses the relationship of the present paper to the existing literature and provides some concluding remarks.
BASIC MODEL
In this section, I describe the basic model without payment uncertainty. Payment uncertainty is introduced in the next section. The economy is comprised of consumers, firms, and a government. In this economy, time is discrete and continues from zero to infinity: t = 0, 1, 2, …, ∞. There are infinitely many consumers who have identical consumption preferences and maximize:

where β (0 < β < 1) is a discount factor, u(c) is an increasing and concave function, and ct is the consumption in period t. The measure of the consumers is normalized to one. There also are infinitely many firms with measure one, which are risk-neutral and maximize profits. Only firms, not consumers, have access to the production technology described later.
Production Technology
I assume the following production technology in order to formalize the division of labor among economic agents in the market.
Consumers are endowed with a nondepletable asset (land), the total supply of which is K, at the initial date, that is, the beginning of period 0. In period t, a firm can produce A(n)k units of good-n from k units of land, where
and A(n) is increasing and concave in n. A firm can also transform y units of good-i (i = 1, 2, …, n) into y units of good-(i − 1). The firm can freely choose y(>0). Only good-0 can be consumed by consumers (good-0 is the consumer good).
A firm must choose in every period whether it produces goods from land and chooses n, or whether it produces good-(i − 1) from good-i (i = 1, 2, …, n).4
Because the production technology is linear (i.e., a firm can set k and y at any amount), the distribution of firms that choose to produce which goods does not matter for determining the aggregate production. For simplicity, I assume that the measure of firms that produce good-i (i = 0, 1, 2, …, n) is
.
There is one technology constraint for firms' production activity: A firm that produced good-i cannot process its own output; another firm must purchase the output from the firm and transform it into good-(i − 1). This constraint can be interpreted as saying that a firm specializes in the production of only one kind of good during period t and cannot use its output for the next-stage production during the same period. This constraint makes the payment process relevant to aggregate productivity.
I assume that the consumer good that is produced during period t cannot be stored or invested for the next period and must be consumed at the end of period t. Otherwise, it perishes at the end of period t. Good-i (i = 1, 2, …, n) also perishes at the end of period t unless it is used for production of good-(i − 1) in period t.
This production technology can be seen as a simplified and stylized model of reality, in which the division of labor among firms in the economy enhances aggregate productivity and at the same time increases the number of payments associated with intermediate transactions. The number n, which is chosen by firms, is the number of steps in a chain of production, and is also the number of payments, which must be made in the chain of production. I use this technology, although it may look ad hoc and awkward, as in the existing literature there is, to my knowledge, no tractable and empirically plausible model that deals with both the division of labor and the number of payments.5
Payment Process
In all transactions by consumers and firms in this economy, payments are made by promissory notes. Settlements of the notes that are issued in period t are made at the end of each period t. There are two kinds of transactions that firms undertake in period t. First, a firm rents land from a consumer to produce good-n. The firm issues a promissory note and gives it to the consumer as payment for the rent. Second, a firm buys intermediate goods (good-i) from another firm to produce good-(i − 1). In this case, too, the buyer issues a promissory note to the seller as payment. At the end of period t, the consumer good (good-0) is produced, and consumers buy good-0 by issuing promissory notes to firms. I assume as follows that firms and consumers act as atomic agents in a competitive market.
Assumption 1. Firms and consumers randomly encounter each other in the market, and they sell and buy goods with each other. The random matching is efficient in the sense that all markets clear every period.
This assumption is crucial to generate payment uncertainty under an environment where many firms operate on the verge of bankruptcy (see Section 3). Firms and consumers redeem their own promissory notes at the end of period t.
Equilibrium
In the competitive equilibrium, consumers and firms solve their optimization problems in the above technological and payment environment, given {Pt, P1t, …,
Qt, Rt}, where Pt is the price of the consumer good, Pit is the price of good-i (
), Qt is the price of land, and Rt is the rent of land. The problem for the representative consumer is:

subject to:

and k0=K, where ct is the consumption in period t and kt is the land holding in period t.
The profit maximization problem for the representative firm when it buys good-i and produces and sells good-(i − 1) during period t is:

where y is the amount of input and output and Pit is the price of good-i during period t. In the equilibrium where there is no uncertainty, it is obvious that Pit = Pi − 1t for i = 1, 2, …, n. Note that P0t = Pt, where Pt is the price of the consumer good at the end of period t.
The profit maximization problem for the representative firm when it rents land from a consumer and produces and sells good-n during period t is:

where k is the land rented and n (
) is the kind of goods that the firm produces. Because Pnt = Pt in the equilibrium where there is no uncertainty, firms choose n to maximize A(n) in the equilibrium:
. The competition among firms implies that in the equilibrium,
.
Because land is a nondepletable asset and good-0 is a perishable good, the equilibrium allocation is simply as follows: Land holdings of the consumer in period t are kt = K, and consumption in period t is
. The first-order conditions (FOCs) for the consumer's problem imply that the real price of land (
) is determined by
.
Therefore, in the competitive equilibrium without (payment) uncertainty, the number of intermediate goods becomes largest (
) and macroeconomic productivity becomes highest (
).
PAYMENT UNCERTAINTY
In order to explain the productivity slowdown of the Japanese economy in the 1990s by this model, I assume that an unspecified one-time macroeconomic shock hits the economy and that it generates nonperforming loans from consumers to a portion of firms with measure z1 (0<z1<1) at the end of period 0, after all payments for transactions during period 0 are settled. I call these z1 firms zombie firms.
Assumption 2. A zombie firm owes a nonperforming loan to only one consumer. The nonperforming loan to the zombie firm is observable only to the firm itself and the creditor. A zombie firm has the same production technology as other firms; therefore, other consumers or firms cannot distinguish it from a healthy firm.
Note that a zombie firm is not inefficient per se in terms of production technology; the only difference is that the creditor has too large of a claim on the (prospective) assets of the zombie firm. The reason why nonperforming loans are generated is not specified in this paper. I simply assume that some exogenous shock (e.g., the emergence and bursting of asset-price bubbles) made some firms overly indebted. I assume that the nominal amount of the nonperforming loans to each zombie firm at the beginning of period 1 (N1) is very large:
.
In what follows, I describe the bankruptcy process and the forbearance policy adopted by the government, and then the equilibrium outcome under this policy.
Bankruptcies
I assume that the government can choose whether or not to make a zombie firm go bankrupt at settlement time, that is, the end of a period. When the firm goes bankrupt, the creditor of the nonperforming loan can seize all the assets of the firm, and all payments from the firm to other creditors are cancelled.6
To make clear the meaning of this assumption, let us consider the case in which a zombie firm continues to operate and conducts production activities during period t. At the end of period t, the settlement time, the firm has as its assets the promissory notes issued by its customers, whereas it has as its liabilities the nonperforming loan Nt from a consumer and the account payable to promissory notes that the firm issued during period t. If this firm goes bankrupt at the end of period t, the creditor (consumer) that holds Nt seizes all the assets (i.e., promissory notes) and cancels payment on the promissory notes that the debtor firm issued. Because the promissory notes issued by the zombie firm were handed to its suppliers (see Assumption 1), when the firm goes bankrupt, other firms incur losses by cancellation of the promissory notes.
The Forbearance Policy
For some political reason, the government wants not to make zombie firms go bankrupt all at once but to make them go bankrupt slowly in a planned manner.7
One reason for making the assumption that the government sets the rate of bankruptcy of zombie firms is as follows. In the early 1990s in Japan, the government announced that the disposal of nonperforming loans (and the rehabilitation of debtors) was to be done gradually and methodically. Because the Ministry of Finance had strong control over banks' operations, it is quite likely that MOF actually determined the pace of disposal of nonperforming loans until the policy regime drastically changed during a financial crisis in the 1997–1998 period. Therefore, the assumption that the government determines x is plausible as a formalization of Japan's forbearance policy toward the nonperforming loans of the 1990s.

I assume that the government cannot set x at zero, but there is a lower bound
such that
.
In order to simplify the calculation, I assume that at the end of period t, bankrupt firms of measure xzt are replaced by newly established firms of the same number, and thus the total measure of the firms remains constant as one.
Firms' Problem
If zombie firms of measure xzt go bankrupt at the end of period t, there emerges a risk that a promissory note will not be settled. Because Assumption 2 implies that a seller cannot tell whether the buyer is a zombie firm or not, sellers become constantly exposed to a positive probability of not being paid. Therefore, prices of intermediate goods are distorted by this payment uncertainty. Consider a (healthy) firm that produces and sells good-(i − 1) in period t. Because the buyer will go bankrupt and fail to pay at the end of the period with probability xzt, the firm maximizes the expected profit:

for i > 1, where y is the amount of input and output. And since consumers do not go bankrupt, the firm that sells good-0 to consumers maximizes P0ty − P1ty. A firm that rents land from a consumer and produces good-n from land chooses n to maximize the expected profit:

given Pt and Rt.
Consumers' Problem
The consumers' problem under the forbearance policy is as follows:

subject to:

given prices [Pt, Qt, (1 − xzt)Rt], the market rate of interest (It), the lump-sum tax (Tt), and the initial values k1 = K and I1 = 0, where the nonperforming loan to a remaining zombie firm evolves by

I assumed for simplicity that consumers obtain (1 − xzt)Rtkt deterministically as a dividend from land kt by, say, forming fair insurance among themselves.
Government's Policy
In addition to setting the bankruptcy rate x, the government sets the lump-sum tax Tt such that it equals the gap between liabilities Nt+1xzt and assets of the bankrupt firms.
Equilibrium
In the competitive equilibrium, consumers and firms solve these problems, given
. The FOCs for firms' problems imply that in the equilibrium where the profit-maximizing firms earn zero profits, prices of intermediate goods are determined by:

Thus, under payment uncertainty, (6) implies that nt is chosen such that
, where:

In the equilibrium, the rent of land becomes:

Note that as there is no real disruption of the production process, the final output of good-0 is A(nt)K even under payment uncertainty, and thus consumption is:

in the equilibrium. A consumer obtains the expected dividend from land of (1 − xzt)Rt, because a firm fails to pay Rt with probability xzt.
The real asset price
is determined by:

The market rate of interest is determined by:

If a zombie firm goes bankrupt, the creditor seizes the remaining assets, which are, on average,
, where kt is land per one firm. Thus, the creditor seizes assets of A(nt)ktPt[1 −(1 − xzt)n+1] by making xzt firms go bankrupt at the end of period t.8
I assume for simplicity that consumers form fair insurance among themselves on asset-seizure such that all consumers get paid the same amount from the bankruptcies of xzt firms.

Welfare Implications
In this stylized model, bankruptcies are just lump-sum transfers of funds among agents. Therefore, bankruptcies per se do not generate direct welfare losses. Welfare losses in this model are solely caused by disruptions of the division of labor.
Let us define an integer t(x) by
for t≤t(x) and
for t>t(x). As long as x is not too small, t(x) is decreasing in x. If x = 1, A(n1) declines sharply but is restored immediately, that is,
for t≥2. Because consumption is proportional to productivity, the utility of consumers [equation (1)] may become smaller if productivity is less than
for longer periods. Thus, if the government sets x at a smaller value, social welfare may become smaller too. In Figure 3, social welfare
is plotted as a function of x, given that u(c) = ln c and A(n) = na. The parameter values are a = 0.2, β = 0.99, K = 1, z = 0.2,
, and
. (Although I did not report this in the figure, I calculated welfare function for a wide range of parameter values. See footnote 9.) The paths of productivity and the real land price for a small x and a large x are also shown in the figure.

Welfare, productivity, and land prices. Parameters: z = 0.2, a = 0.2, β = 0.99, K = 1, x = 0.01, $\bar{n}\,{=}\,1000$.
In the region of 0.016<x<1, welfare is increasing in x, implying that immediate bankruptcies of zombie firms bring about the highest welfare for consumers.9
The result that a larger x brings about higher welfare is robust for a wide range of parameter values. The region in which welfare is increasing in x becomes narrower as
and β become smaller. But even in the case in which
and β = 0.8, welfare is increasing in x in the region of 0.3<x<1.
to be an exogenous process that is independent of x. In this case, a benevolent government, wanting simply to maximize social welfare, may set x at such a small value that it unintentionally causes productivity to stagnate.
Equation (13) shows that land prices may also stagnate, mainly for two reasons. One is the stagnation of productivity, and the other is that some of the dividends from land, that is,
are seized by the creditors of nonperforming loans through bankruptcies of zombie firms. This second reason implies that the land price qt is still less than
even at t>t(x) when
. Although it is not evident visually, Figure 3 shows that the land price for x = 0.1 is lower than that for x = 0.9 even at ∀t>t(0.1).
COMPARISON WITH THE JAPANESE ECONOMY
This model can be easily embedded in a standard growth model, in which the representative consumer accumulates capital stocks. I assume in this section that at each period t, a firm produces the initial good (good-n) from capital stock kt and labor input lt, not from land as in the previous sections. The production technology is Cobb-Douglas:
, where 0<α<1, and the representative consumer supplies one unit of labor at each period inelastically. Therefore, the reduced form of the consumer's problem under the government's forbearance policy toward zombie firms is to maximize (1) subject to:

where δ is the depreciation rate and nt is defined by
, where
is determined by (10). The consumer chooses ct and kt+1, taking A(nt) as given. Note that no distinction between consumer goods and capital goods is made. Assuming that u(c) = ln c, the dynamics of the economy are described by the following difference equation:

This equation is numerically solved under the assumption that the economy is in the steady state in period 0 (before shock z hit the economy). The steady state value of capital stock (kSS) is determined by:

as productivity is constant at
in the steady state. The welfare implication is the same as that in the previous section: Social welfare
is an increasing function of x for 0.01<x<1. Figure 4 shows the dynamics of the macroeconomic variables for x = 0.1 and x = 0.9 in the model. Figure 5 shows the values of corresponding variables in Japan in the 1990s.

Paths of model variables (the extended model with capital accumulation). Parameters: z = 0.2, a = 0.2, α = 0.3, β = 0.99, x = 0.1 or 0.9, δ = 0.01, $\bar{n}\,{=}\,1000$.

Performance of the Japanese economy in the 1990s. Sources: Hayashi and Prescott database, http://www.e.u-tokyo.ac.jp/~hayashi/Hayashi-Prescott1.htm; Bank of Japan home page, http://www.boj.or.jp. Note: The data except for interest rates are detrended at 2% and normalized to 100 for 1990. The real interest rate is the interest rates on certificates of deposit with maturities ranging from 180 days to one year (new issues) at the end of the calendar year minus the rate of change of the GNP deflator constructed by Hayashi and Prescott.
Because Figure 4 shows the impulse responses to the one-time shock z at the end of period 0, there are several significant differences between the paths of the model variables and those of their real counterparts. There are, however, some similarities between the case of x = 0.1 in Figure 4 and Figure 5. Consumption and the (ex post) real interest rate in Japan exhibited significant declines in the 1990s. These patterns are replicated by the paths of the model variables: Consumption initially declines after the shock hits the economy, and the real interest rate stays below its steady state level for a long period.
The model seems to fit the data considerably well, and a more accurate fit could be obtained by introducing multiple shocks to the payment process. Because land prices in Japan continued to decline, falling short of people's expectations every year, multiple shocks to the payment process seem to be a plausible assumption.
LITERATURE AND CONCLUDING REMARKS
The mechanism of the productivity slowdown described in Section 3 is consistent with the finding by Hayashi and Prescott (2002) that Japanese corporations were able to find financing for investments in the 1990s. They claim that a credit crunch or other problems with financial intermediation may not be the culprit in Japan's decade-long recession.10
Hosono and Watanabe (2002) also confirm empirically that the liquidity constraint for Japanese firms did not become more severe in the 1990s. Andolfatto (2003) also argues that monetary and financial problems in Japan's lost decade may be irrelevant to the output decline.
The decline in productivity in this paper is ultimately driven by the disruption of the division of labor among firms. This mechanism is similar to Blanchard and Kremer (1997) and Kobayashi (2004). The novelty of the present paper is that the endogenous disruption of the division of labor occurs through the price mechanism in the market, in which firms trade intermediate goods as anonymous sellers or buyers. The other papers assume that firms form a team for production explicitly, and the results in these papers may therefore crucially depend on the specific assumptions on relationships among firms in a team. The results in the present paper do not depend on any strategic relationships among firms, and thus they hold under more general environments. In order to check disruption of the division of labor, Kobayashi and Inaba (2005) conducted an empirical analysis using the Input-Output Tables. We found that productivity declined more in industries with a more complex input-output structure in the early 1990s in Japan and that the productivity decline was more severe in industries with heavier debts.
Payment uncertainty associated with promissory notes (or trade credits) plays a central role in the disruption of the division of labor in this model. Kiyotaki and Moore (1997) and Calvo (2000) address the problem of trade credits, and they propose theoretical models in which a disruption of a chain of trade credits amplifies a recession. The basic structure of their models is that a liquidity shortage is amplified through disruption of the chain of credits, and it seems to explain a sharp and temporary recession associated with a liquidity crisis or a credit crunch, although not a decade-long slowdown of productivity growth of the kind observed in Japan. In my model, persistent payment uncertainty, not actual disruption of credit chains, causes shrinkage of the division of labor. Because the risk of not being paid persists because of the forbearance policy, and actual disruptions of credit chains seem short-lived, the model in this paper may better explain Japan's lost decade.
In this model, payment uncertainty, that is, a risk of not being paid, is faced by new creditors and suppliers, not by incumbent creditors that roll over bad loans to zombie firms. Lamont (1995) argues that investments and outputs may inefficiently shrink if new creditors have a risk of not being paid in full because incumbent creditors take most of the outputs. Although the Lamont model shares the thinking of my model in some respects, it does not show a decrease in productivity, whereas it does show that a decrease in investments can be caused by a demand shortage in an economy of monopolistic competition.
The productivity slowdown in Japan's lost decade is and will continue to be a big puzzle. In this model, I presented a possible mechanism of productivity decline, which is that the government's forbearance policy kept nonviable zombie firms afloat and raised payment uncertainty for other firms. This causes endogenous lowering of the level of the division of labor and thus of aggregate productivity.11
A disruption of the division of labor due to payment uncertainty also may explain TFP declines in ordinary recessions, as it usually takes some time for nonviable firms to go bankrupt, and they raise payment uncertainty until they stop operating.
I am grateful to Takeo Hoshi and anonymous referees for helpful comments.