INTRODUCTION
Taking Dutta and Kapur (1998) as a particular case of the Tobin effect (Tobin, 1955, 1965), this note investigates the extent to which the Tobin effect persists with the addition of sophisticated financial instruments in the context of incomplete markets. As discussed by Woodford (1990) and others, incomplete markets and seigniorage redistribution among heterogeneous agents may be jointly responsible for the positive welfare impact of monetary expansion or the emergence of the Tobin effect. The model constructed by Dutta and Kapur (1998) presents an important case where optimal inflation rates are positive by considering these two aspects explicitly; that is, financial markets are incomplete in the sense that physical assets are irreversible and noncollateralizable, and that any insurance contract is not available, while seigniorage revenues are redistributed to young agents who make irreversible investments.
A possible response to this implication is that once agents are allowed to self-insure against idiosyncratic shocks by borrowing or to make dynamic insurance contracts in advance, money demand as a precautionary device disappears completely, and there is thus no room for the Tobin effect to hold any longer. In other words, the Tobin effect may not be robust with respect to the introduction of sophisticated financial instruments. As shown later, the case of Dutta and Kapur (1998) is indeed subject to this kind of criticism.
This note instead explores the extent to which limited usage of financial instruments still maintains the Tobin effect. We attempt to present a case where the Tobin effect is not weakened, but strengthened with the introduction of financial instruments in a limited manner. More concretely, we make a case where the Tobin effect persists under coexistence of fiat money and dynamic insurance contracts given a limited size of insurance transfers between consumers.
A principal reason for the above consequence is that dynamic insurance contracts compete with fiat money in terms of intertemporal allocation. As explored in existing papers, including Townsend (1982), Green (1987), and Thomas and Worrall (1990), dynamic insurance contracts combine intertemporal allocation with intratemporal risk sharing. For example, in Townsend (1982), which assumes no alternative investment opportunity, the extent to which incentive compatibility conditions are binding depends crucially on how low the risk-free return implied by an autarkic resource allocation is. That is, the lower the implied return, the less binding the incentive compatibility condition, and consequently the better the potential insurance performance. Conversely, given alternative investment opportunities with good returns, the provider (the principal) of a dynamic insurance contract competing with such alternatives offers high returns to the insured (the agent) to the detriment of insurance performance.1
For example, Allen (1985) shows that when the agent is able to secretly borrow and lend at the same rate as the principal, no incentive-compatible contract can improve on self-insurance by lending and borrowing at that rate. In addition, Cole and Kocherlakota (2001) demonstrate that when the agent is able to take a long position (but no short position) on alternative investment opportunities with sufficiently high returns, the trading of risk-free bonds between agents mimics the efficient resource allocation induced by dynamic incentive compatible contracts.
In our context, because returns on fiat money as an alternative device decrease with higher rates of inflation, the incentive compatibility condition in an inflationary environment is relaxed to some extent, so that more efficient insurance contracts can be implemented. We demonstrate that such a constraint-relaxing effect, in addition to the seigniorage-transfer effect emphasized by Dutta and Kapur (1998), can offset the cost of holding money when steady-state rates of inflation are relatively low.
Aiyagari and Williamson (2000) is the paper most closely related to our investigation.2
Although not in the context of dynamic insurance contracts, previous papers such as Farmer (1988) and Kitagawa (2001) also pay serious attention to the effect of monetary policy on contract constraints.
Among models where fiat money coexists with insurance, Hornstein and Krusell (1993) incorporate into a turnpike model of fiat money partial insurance contracts contingent only on public information. However, there are no roles of insurance markets in revealing private information within their framework.
Kim (2003) extends the work of Aiyagari and Williamson work to an AK growth model and presents a case against the Tobin effect. Because an increase in physical capital makes incentive compatibility more binding, an inflationary policy shifts savings from money to capital, thereby making welfare more deteriorating.
This paper is organized as follows. In Section 2, we present a monetary model with a two-period insurance contract to examine how the Tobin effect persists using numerical examples. Section 3 offers a conclusion.
A MONETARY MODEL WITH DYNAMIC INSURANCE CONTRACTS
A Modified Version of Dutta and Kapur (1998)
This section first presents an overlapping generations model comprising three cohorts, following Dutta and Kapur (1998). As a minor modification to their model, we substitute unobservable idiosyncratic income shocks for preference shocks, so that simple dynamic contracts may be introduced into the model later in a fairly simple manner.
The economy has three overlapping generations, the young, middle-aged, and elderly. An infinite sequence of generations allows a government to issue fiat money handed from one generation to another. The population of each cohort is constant over time and standardized to unity. A young consumer is endowed with y0 units of goods. A middle-aged consumer earns an independently and identically distributed (i.i.d.) income of yh with probability
and yl with probability
, where yh>yl and ya
. There is no endowment for elderly consumers.
A young consumer can make a physical investment of I units, and earns 1+r per unit of investment over a lifetime. Investors can neither reverse nor collateralize their investment in middle age. These assumptions are reasonable when investment by young agents is not observable. Given that investment is irreversible and noncollateralizable, middle-aged consumers cannot insure themselves against idiosyncratic shocks using physical investment as a precautionary instrument.
Both young and middle-aged consumers may hold fiat money m, the value of which depreciates with a rate of inflation π each period. In the absence of an insurance contract, only fiat money can play an essential role as self-insurance against the income fluctuations of middle-aged consumers in this environment. Any seigniorage revenues s are assumed to be redistributed to young consumers in the form of a lump-sum transfer.
Henceforth, we restrict our attention to a steady-state equilibrium and omit time subscripts. A young consumer maximizes an expected logarithmic utility function by choosing middle-aged consumption and elderly consumption as follows:5
Our final results presented later in this section do not depend on the logarithmic form of the utility function; in fact, the welfare impact is enhanced by higher degrees of risk aversion. Numerical results for nonlogarithmic cases are available upon request.

where
(
) is middle-aged consumption, and
(
) is elderly consumption, given a realization of middle-aged income of yh (yl).
In the current framework, neither insurance contracts nor self-insurance by borrowing is available, and only fiat money can provide self-insurance against income fluctuations during middle age. Thus, utility maximization is subject to the following budget constraints. With a realization of either yh or yl, we have


and

or

where I is irreversible physical investment and m is the real value of fiat money held by a young consumer. Note that m is nonnegative (m≥0).
If 1+r>(1−π)2, then the liquidity constraint (2) should be binding for either high- or low-income earners. In this paper, we focus on the most plausible case, in which the budget constraint (2) is binding for only middle-aged low-income earners. That is, as a result of liquidity constraints,
, and
for low-income earners, while as a consequence of consumption smoothing,
for high-income earners.6
In fact, with respect to idiosyncratic shocks to time preferences, Dutta and Kapur (1998) consider essentially the same case, in which the budget constraint is binding only for a group of impatient consumers.
As there are only goods and fiat money markets, by Walras's law the following market-clearing condition for the goods market implies equilibrium in the money market:

To maintain steady-state monetary equilibrium, nominal money supply M must increase by Mt+1−Mt=sPt+1=s(1+π)Pt (P is a nominal price) according to the government budget constraint. It is straightforward to show that zero inflation (π=0) implies zero seigniorage (s=0).
Given money demand m, an indirect utility V is derived by substituting the above budget constraints of both high- and low-income earners into equation (1). For money demand m to be positive, the first derivative of V with respect to m at m=0 should be positive, or
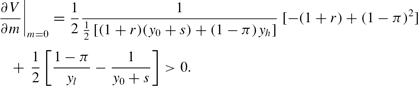
In this equation, the first term on the right-hand side (marginal utility in the high-income state) is negative, while the second term (marginal utility in the low-income state) may be positive. The condition expressed by equation (4) implies that with greater middle-aged income fluctuations (yh−yl), lower rates of inflation (π), or poorer returns on irreversible investment (r), money demand m is more likely to be positive.
As the following proposition demonstrates, the above framework shares with Dutta and Kapur (1998) the local property that welfare improves when a small-scale monetary expansion is implemented at zero inflation (s=π=0), a property also known as the Tobin effect.
PROPOSITION If only low-income earners are subject to liquidity constraints, and m is positive, then steady-state welfare V improves with a marginal increase in s from s=0 (π = 0).
Proof. See the Appendix.
As demonstrated in numerical examples later, the current model also exhibits a global property that an expansionary monetary policy with s>0 is welfare-improving if the cost of holding money is not excessive at moderate rates of inflation. These policy consequences, local and global, are crucially due to a seigniorage transfer to young consumers who make irreversible but productive investments in the context of incomplete markets.
Hereafter, we maintain the following assumption on both technology and endowment: ya=y0(1+r)=1. Under this assumption, the first-best steady-state allocation, which is attainable from complete markets, achieves complete consumption smoothing, in which the consumption distribution is given by
The corresponding expected utility V is then equal to zero.
Our main results do not depend on this simplifying assumption, as long as in an autarkic resource allocation, high income yh (low income yl) is larger (smaller) than the long-run investment outcome y0(1+r). However, this assumption is convenient in the following respects. First, as mentioned above, if markets are complete, then ex ante identical consumers can attain complete consumption smoothing by investing the whole initial endowment in the long-run productive technology. Therefore, we can easily evaluate the impact of market incompleteness by the extent to which the equilibrium consumption profile deviates from perfect smoothing as a result of shifts from productive capital to fiat money in a monetary equilibrium. Second, as shown later, alternative forms of dynamic contracts (such as risk-free bonds and full-fledged dynamic insurance) can be derived in a simple closed form under this assumption. Accordingly, it is fairly easy to make a comparison among different dynamic arrangements.
Introduction of Dynamic Insurance Contracts
As mentioned above, the unobservability of middle-aged income fluctuations may allow for the absence of insurance contracts, while the unobservability of investment behavior by young agents may justify the irreversibility and the noncollateralizability of physical investment. However, consideration of periods following the one in which middle-aged incomes are realized may enable two-period insurance contracts to be introduced for middle-aged incomes in this framework, thereby revealing private information on middle-aged incomes in an incentive-compatible manner.7
In practice, the introduction of dynamic contracts requires that agents on contracts be identifiable throughout their lives.
The replacement of fiat money by dynamic contracts
A simple way to introduce a dynamic arrangement is to enable low-income middle-aged earners to borrow against future fruits of irreversible investment by making physical investment still irreversible, but collateralizable. Then, completely replacing government-issued fiat money with privately issued risk-free bonds (m=0), low-income earners maximize ln(yl+ρl)+ln [(1+r)y0−dρl] or ln(yl+ρl)+ln(1−dρl), while high-income earners maximize ln(yh−ρh)+ln(1+dρh) with respect to ρl or ρh (the amount of privately issued risk-free bonds) given d (gross risk-free returns in this context). Note that (1+r)y0=1 by assumption.
Given the market-clearing condition ρl=ρh, the equilibrium risk-free rate is equal to unity, while equilibrium lending from high-income to low-income earners is

Note that even low-income earners are not subject to liquidity constraints by construction, and hence there is no demand for money as a precautionary device in this case.
Another dynamic arrangement to be introduced is the dynamic insurance contract shown by Townsend (1982) where, if two-period contracts are made not ex post, but prior to the realization of middle-aged incomes, dynamic insurance contracts not only mitigate the moral hazard problem relating to incentive compatibility conditions, but also yield higher expected utility for young investors. In such optimal dynamic insurance, two-period insurance payoffs are contingent on voluntary reports of realized incomes from each middle-aged consumer.
Following Townsend (1982), for simplicity and convenience we adopt the following parameterization for insurance payoffs. On the one hand, insurance payoffs for high-income earners are “back-loaded” with contributions in middle age and benefits in old age. That is, there is a pair of −ρ and +dρ, where ρ>0 and d>0. On the other hand, payoffs for low-income earners are “front-loaded”; there is a pair of +ρ and −dρ.
In the context of the above payoff structure, a larger ρ and a smaller d imply greater insurance cover for fluctuations in income in middle age. The transfer of ρ from high-income earners to low-income earners during middle age functions in the same way as standard insurance payoffs. As shown subsequently, the transfer of dρ from low-income earners to high-income earners during old age serves as an incentive device forcing high-income earners to be honest. Hence, d can be interpreted as the agency cost of mitigating asymmetric information problems. A dynamic contract with both
and d=0 (zero agency costs), if enforceable, would provide complete insurance cover.
Suppose that fiat money is replaced completely by dynamic insurance (m=0). To keep high-income earners from reporting their incomes dishonestly, the following incentive compatibility condition must be satisfied:

Note that (1+r)y0=1 by assumption.
Raising ρ to the power of both sides of the above equation yields
The left-hand side of this equation is equal to the risk-free rate implied by the autarkic allocation for high-income earners (yh for middle-aged high-income consumers and unity for elderly consumers). This implies that the internal rate of dynamic insurance d should equal or exceed the autarkic risk-free return. Notice that the autarkic rate is below the equilibrium one-period risk-free rate (
), and hence dynamic insurance incurs lower agency costs than does trading risk-free bonds.
With this binding incentive compatibility constraint
, the optimality condition requires that

should be maximized with respect to ρ. Thus, the optimal level of transfer ρ** is equal to

where
It follows from the above optimality condition that the two-period incentive compatibility contract provides greater insurance cover than does self-insurance from issuing risk-free bonds. That is, there are larger transfers during middle age (ρ**>ρ*), and lower agency costs are incurred during old age (
). Clearly, given this optimal insurance contract, there is no demand for money as a precautionary savings device.
Coexistence of dynamic contracts with fiat money
In monetary models with incomplete markets, the introduction of sophisticated contracts with wide insurance coverage would often crowd out money demand completely. Aiyagari and Williamson (2000) impose some restrictions on insurance performance to keep money demand from disappearing. More concretely, they consider the possibility that consumers on contracts are temporarily excluded from receipts of contingent payoffs with a positive probability. As a result, consumers may still hold money in preparation for such a temporal exclusion.
We introduce a similar mechanism in a rather different manner. As shown previously, a full-fledged insurance contract involves large-scale transfers between contracting parties at maturity. However, such contracts with large transfers may not be fully enforceable. Given limited enforceability, upper limits of transfers may be determined to the extent that payees can seize assets held by payers for their benefits. If part of the assets are not collateralizable, or they belong to private benefits, then it is rather difficult for payees to seize payers' assets completely. Therefore, it may be more realistic to impose restrictions on the size of insurance transfers. Given limited transfers between middle-aged consumers, young agents would still have an incentive to hold money to compensate for such partial transfers. Thus, money would coexist with insurance.
Considering the point above, we assume that transfers within the same cohort are rather smaller than those for self-insurance with risk-free bonds
where all agents are free from liquidity constraints. Defining the size of the transfer ρ as

we choose α (0<α<1) such that the money demand of young investors may be positive. A possible interpretation of equation (6) is that a parameter α represents the extent to which physical investment (1+r)I is collateralizable at contract maturity, à la Kiyotaki and Moore (1997) where incomplete contracting requires collateral to prevent renegotiation of the terms.
Although the size of insurance transfers ρ is determined exogenously, the incentive compatibility condition is still able to fix the internal return on dynamic contracts d endogenously. Because fiat money now competes with dynamic insurance contracts as an alternative investment opportunity, high-income earners (savers) compare the performance of dynamic insurance with that of holding money. Therefore, provided that the internal return on back-loaded payoffs (d) is greater than or equal to the return on fiat money as an alternative (1−π), the nature of the back-loaded payoffs prevents high-income earners from reporting dishonestly. Thus, the incentive compatibility condition is given by
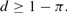
As before, d represents the degree of insurance efficiency; the lower d is, the smaller are agency costs. Hence, this incentive compatibility is binding for a second-best insurance contract, or d=1−π.
According to intensive numerical calculations, if α is well below unity, then money demand m is positive. The next subsection makes a remark on how small α should be to obtain the coexistence case as a main result. In the case of coexistence, the following budget constraints are obtainable. With a realization of low income, we have
and
while with a realization of high income, we have

with the binding incentive compatibility condition d=1−π.
Numerical Examples
Numerical examples in this section demonstrate that the Tobin effect persists in the case of coexistence of insurance contracts and fiat money. There are two competing effects on the optimal steady-state rate of inflation in this environment. A wider insurance cover against idiosyncratic shocks generally leads to higher real returns on risk-free assets (that is, returns closer to time preference rates) in the real economy, and leads to lower rates of inflation (higher rates of deflation) with weaker money demand in the monetary economy. In this regard, the introduction of dynamic insurance contracts, though limited, generates overall downward pressure on equilibrium rates of inflation π. However, as equation (7) implies, incentive compatibility conditions would be relaxed by higher rates of inflation, so that more efficient insurance contracts could be implemented in an inflationary environment. This dependence of incentive compatibility constraints on inflation rates would mitigate the welfare cost of holding money due to inflation, and thereby contribute to an increase in equilibrium rates of inflation with welfare improvement.
These competing effects on the optimal steady-state rate of inflation are illuminated by the following numerical examples. As suggested in the previous section, if middle-aged income fluctuations (yh−yl) increase, if returns on irreversible investment (r) fall, or if insurance coverage (α) is narrower, then money demand m is more likely to be positive. For example, Figure 1 depicts ranges for insurance coverage (α) and income volatility (
) for positive values of money demand (m) when r=0.2, d=1, π=0, and s=0.8
Note that the incentive compatibility condition (7) and the market-clearing condition (3) are satisfied when d=1, π=0, and s=0.

Conditions for positive money demand
Motivated by these numerical properties of money demand, we choose a set of parameters as follows. To obtain conditions under which money demand is positive, we choose low returns on irreversible investment (r=0.05), volatile income fluctuations (
), and moderate insurance coverage (α=0.3). We set a seigniorage level (s) that is consistent with a given steady-state rate of inflation (π), so that equation (3) is satisfied, and calculate the welfare gain relative to autarky corresponding to each steady-state rate of inflation. Given the above set of parameters, as long as α is smaller than 0.76, positive money demand (although rather small when α is above around 0.6) can coexist with dynamic insurance with binding incentive compatibility at the optimal rate of inflation.
We suppose the following three cases: (1) there exists no insurance contract; (2) insurance contracts promise payoffs that are independent of inflation rates; and (3) insurance contracts have binding incentive compatibility. The first case corresponds to the one analyzed in Dutta and Kapur (1998), where there is no alternative to holding money. In case (2), the degree of insurance efficiency d is constant and is set to unity regardless of all positive rates of inflation π.9
In this case, equation (7) is not binding, but it is satisfied.
Figure 2 depicts the welfare gain relative to autarky corresponding to each steady-state rate of inflation, and thereby indicates the optimal rate of inflation for the three cases. When there are no insurance contracts, the optimal rate of inflation (denoted by a square) is positive because of the effect of the seigniorage transfer to young consumers who make irreversible decisions. More precisely, such a seigniorage transfer promotes irreversible but productive investment, so that it may mitigate the welfare cost of holding money due to inflation. As welfare costs of money holdings are associated with rising inflation, the optimal rate of inflation is moderate.

Welfare gain relative to autarky. Steady-state inflation rate: (—) w/o insurance, (—) w/i insurance (IC binding), (- - -) w/i insurance (independent payoff)
When insurance payoffs are independent of inflation rates, overall welfare is higher due to the insurance effect, while steady-state rates of inflation are lower. In that case, the curve represented by the dotted line shifts to the northwest in Figure 2. Consequently, the optimal rate of inflation (denoted by a triangle) in Figure 2 is lower than in the previous case in which there are no insurance contracts.
When incentive-compatible contracts are binding, as a result of the constraint-relaxing effects, the optimal rate of inflation (denoted by a circle) in Figure 2 is higher than when insurance has inflation-independent payoffs. In other words, the constraint-relaxing effect cancels out the downward effect of insurance on steady-state rates of inflation. For the following reason, the optimal rate of inflation is the same as when there are no insurance contracts. As equation (8) indicates, due to indifference between insurance and money, the budget constraint of high-income earners is reduced to the one that applies in the absence of dynamic insurance contracts. Consequently, the first-order conditions of the optimization problems are the same.
These numerical examples demonstrate that the presence of a constraint-relaxing effect, in addition to the seigniorage-transfer effect emphasized by Dutta and Kapur (1998), contributes to the maintenance of the Tobin effect with larger welfare impacts at the same optimal rate of inflation.
CONCLUDING REMARKS
This paper has examined interaction between monetary policies and dynamic insurance contracts when fiat money coexists with dynamic contracts as a result of limited insurance coverage. In particular, it has demonstrated that incentive compatibility constraints could be relaxed with higher rates of inflation in a moderately inflationary environment, so that more efficient insurance contracts can be implemented there. This dependence of incentive compatibility constraints on inflation rates mitigates the welfare cost of holding money due to inflation and thereby sustains the optimal steady-state inflation rate at a positive level. Consequently, the Tobin effect could persist even with the addition of sophisticated financial contracts in the case of coexistence of money and insurance.
APPENDIX: A PROOF OF THE PROPOSITION IN SECTION 2
When only low-income earners are subject to liquidity constraints, given positive money demand m, an indirect utility V is derived by substituting budget constraints into equation (1). The derivative of this indirect utility V with respect to s evaluated at s=π=0 reduces to
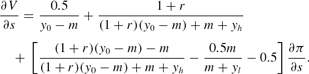
From total differentiation of the market-clearing condition (equation (3)),

is obtained when s=π=0. Substituting equation (A1.2) into equation (A.1), and rearranging yields

at s=0, because
and
when only low-income earners are subject to liquidity constraints.
The authors acknowledge helpful and encouraging comments from an anonymous referee, Naohito Abe, Kosuke Aoki, Toni Braun, Roger Farmer, Shin-ichi Fukuda, Akiomi Kitagawa, Kenji Miyazaki, Shinsuke Nakamura, Akihisa Shibata, and seminar participants at Tokyo, Kyoto, Osaka, Hitotsubashi, and Keio Universities and the Bank of Japan. We are also grateful for grants from the Economic and Social Research Institute, the Cabinet Office, Japan. The first author is thankful for a grant-in-aid from the Ministry of Education and Science, Japan.




