INTRODUCTION
The Divisia approach to monetary aggregation pioneered by Barnett (1978, 1980, 1982) has enjoyed widespread usage in economic research. Moreover, as financial innovation has led economists to focus on broader monetary aggregates, the Divisia approach has become increasingly attractive relative to conventional monetary aggregates [see Lucas (2000)]. Divisia aggregates are now published by the Bank of England [Hancock (2005)] and the Federal Reserve Bank of St. Louis [Anderson, Jones, and Nesmith (1997)]. In addition, Stracca (2004) investigates a synthetic Divisia index for the Euro area [see also Barnett (2003)]. In the Divisia approach, a necessary condition for a monetary aggregate to exist is that the components of the monetary aggregate form a weakly separable grouping. We test groups of UK household sector monetary assets for weak separability over the post-ERM period (1992:4–2005:1) using nonparametric tests and the new data underlying the Bank of England's recent benchmark revision of its household sector Divisia index. Based on the results of these tests, we construct Divisia aggregates for four asset groupings. We then investigate their information content with respect to inflation and nominal output growth and we test whether or not these Divisia aggregates have direct effects on aggregate demand.
Short-term interest rates are the focus of U.K. monetary policy actions in the current inflation targeting framework. Nevertheless, Nelson (2003, p. 1030) argued that even if actual monetary policy can be approximated by an interest rate rule that does not explicitly contain a money term, this does not preclude an important role for monetary aggregates in the transmission of monetary policy or the analysis of inflation. Nelson (2002, p. 705; 2003, p. 1032) argues that money can convey information about economic conditions not summarized by short-term interest rates, because a “spectrum of yields” matter for the determination of both aggregate demand and money demand. With respect to the relationship between money and inflation, Nelson (2003, p. 1045) concluded that the proposition that inflation is always and everywhere a monetary phenomena remains valid in present-day New Keynesian macroeconomic models, irrespective of the monetary policy regime, and that it can be applied to both steady state inflation and inflation dynamics. In a largely dissenting opinion, Svensson (2003, p. 1070) argued that “ … to the extent that money has information about the underlying state of the economy … it makes perfect sense and is completely uncontroversial to use money as one indicator among others.” Ultimately, he argued, the indicator role for money is an “empirical issue, without ideological overtones.”
Belongia (1996) showed that the qualitative conclusions of several important empirical studies were reversed when Divisia aggregates were used instead of conventional “simple sum” monetary aggregates. He argued that (unlike Divisia aggregates) conventional aggregates do not internalize pure substitution effects. He emphasized, however, that the composition of the monetary aggregates must be based on weak separability tests. Weak separability implies that the marginal rates of substitution between pairs of assets in the aggregate are independent of the quantities of all variables that are not in the aggregate. This, in turn, implies that the monetary aggregate is unaffected by pure shifts in the composition of spending on nonmonetary goods. Thus, the monetary aggregate depends on total income and does not depend on the composition of expenditures [Swofford and Whitney (1991, p. 752)].
In this paper, we use nonparametric tests to identify weakly separable groupings of household sector monetary assets for the United Kingdom. One major innovation in our study is that we use new underlying data from the Bank of England's recent benchmark revision of its widely used household sector Divisia index [Hancock (2005)]. The benchmark revision affected several key aspects of how their Divisia index is constructed. In particular, the revision affects how the benchmark rate, which is used to calculate user costs for the monetary assets, is constructed and how break-adjusted and non–break-adjusted monetary asset data are used. A second innovation is that we use the most advanced nonparametric tests of weak separability currently available. We initially use the test proposed by Fleissig and Whitney (2003). If that test rejects, then we employ an unbiased joint test of the necessary and sufficient conditions for weak separability proposed by Swofford and Whitney (1994).
Our weak separability analysis focuses on the post-ERM period, which is appealing since there is a single monetary policy regime over the sample period.1
See Patterson (1991), Belongia and Chrystal (1991), and Drake (1997) for studies of earlier periods.
In an earlier version of this paper, we tested these four groupings for weak separability using data from 1985 to 2000. Weak separability was rejected for all four groupings over the full sample, but better results were obtained by partitioning the full sample into three subsample periods. In this version of the paper, we present results for only the most recent sample period, which we extended up through 2005, following several suggestions of the referees.
Based on these results, we construct household sector Divisia aggregates for these four groupings and investigate their properties in two empirical applications. Our first application is based on Estrella and Mishkin (1997). Several recent studies have examined the forecasting abilities of monetary aggregates, including those of Estrella and Mishkin (1997), Stock and Watson (1999), Schunk (2001), Drake and Mills (2005), and Elger, Jones, and Nilsson (2006). In particular, Estrella and Mishkin (1997) investigated whether monetary aggregates could play a role in the conduct of monetary policy in the United States either in an informal way as information variables or in some more ambitious way. Money could, for example, be used to signal the policy intentions of the central bank. Such more ambitious uses presuppose that the aggregates have some value as information variables. We estimate a trivariate VAR model that includes nominal output growth, inflation, and nominal money growth and apply causality tests to determine if money helps predict the other two nominal variables, following Estrella and Mishkin (1997). Our main findings are that the growth rates of the four nominal Divisia aggregates help predict nominal output growth, but that generally they do not appear to help predict inflation.
Our second application is based on Nelson (2002), who investigated whether or not real balances enter into backward-looking specifications of the IS curve for the United States and the United Kingdom. He found evidence that the real monetary base had “direct effects” on aggregate demand meaning that it had explanatory power for aggregate demand that is not captured by the short-term real interest rate. In particular, real monetary base growth enters the IS-curve “sizably, positively, and significantly” for both countries [Nelson (2002, p. 693)]. In contrast, he cites evidence for the United States indicating that lags of the broad M2 monetary aggregate were invariably insignificant in the IS-curve. We find that all four of the Divisia monetary aggregates we consider have direct effects on aggregate demand for the United Kingdom.
NONPARAMETRIC WEAK SEPARABILITY TESTS
We test whether groups of household sector monetary assets are weakly separable from consumption goods and services and all other (if any) household sector monetary assets. A group of monetary assets is said to be weakly separable if a subutility function separates them from all other variables in the utility function, which implies that the marginal rates of substitution between pairs of assets in the weakly separable grouping are functions only of the quantities of assets within the group.
In what follows, particular observations are denoted by a superscript i, where i runs from 1 to T. Let
and
denote the vectors of observed quantities and prices for all n variables. Let also xi =(yi, zi) and pi =(ri, vi) denote partitions of the quantity and price vectors into two groups. In the partition,
denotes the quantities of the monetary assets being tested for weak separability with user cost prices
, and
denotes the quantities of all other variables with prices
.
Varian (1982) showed that if a data set satisfies the generalized axiom of revealed preference (GARP), then there exists a utility function such that the quantity data maximize that utility function given prices and expenditure for all observations. Varian (1983) derived the necessary and sufficient conditions for weak separability.
Swofford and Whitney's Weak Separability Test
Swofford and Whitney (1994) proposed a joint test of the necessary and sufficient conditions for weak separability. Their test for weak separability of y from z is to minimize the objective function:

subject to
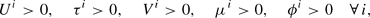


If no feasible solution is found to (2)–(4), then the data are inconsistent with weak separability of the y goods from the z goods. If a feasible solution is found and G can be minimized to exactly zero, equivalently μiϕi−τi = 0 ∀ i, then the data satisfy Varian's (1983) necessary and sufficient conditions for weak separability.3
Swofford and Whitney (1994) also discuss the case when a feasible solution is found, but the objective function is not minimized to zero, which they interpret as weak separability with incomplete adjustment. We do not consider the possibility of incomplete adjustment in this paper.
Fleissig and Whitney's Weak Separability Test
A less computationally burdensome test can be based on constructing positive indexes
satisfying (3) without reference to (4) using a numerical algorithm and then testing
for GARP. If either of the two necessary conditions is violated or this additional GARP condition is violated, then weak separability is rejected. If none of the three conditions are violated, then weak separability is accepted. Fleissig and Whitney (2003) provide a linear programming algorithm for constructing such indexes, which they employ in their weak separability test. Their test could, however, incorrectly reject weak separability, because the necessary and sufficient conditions are tested sequentially rather than jointly as in Swofford and Whitney's (1994) test. In our empirical work, we initially run Fleissig and Whitney's (2003) test and if that test rejects, then we run Swofford and Whitney's test.
DATA FOR WEAK SEPARABILITY TESTS
Our weak separability analysis is based on quarterly seasonally adjusted data and focuses on the post-ERM period 1992:4–2005:1. This period is appealing, as there is a single monetary policy regime over the entire sample. In this section, we provide a description of the data used in our weak separability tests.
Nonmonetary Data
We use data on the eight components of nondurable goods and the 10 components of services as defined by the Office for National Statistics (2005).5
The data are available in Tables 6.2 and 6.3 in Office for National Statistics (2005).
Home population figures were obtained from DataStream. Population figures for 2004 and 2005 are estimates from the Government Actuary's Office.
Monetary Data
We use break-adjusted quantity data on five monetary assets included in the Bank of England's household sector Divisia index: Notes and Coins (NC); non–interest bearing bank deposits (NIBD); interest bearing bank sight deposits (IBSD); interest bearing bank time deposits (IBTD); and total building society deposits (BSD). We aggregate NC and NIBD into a single component, which we call non–interest bearing monetary assets (NI).7
See Hancock (2005) for extensive discussion regarding the way break-adjusted data is used in the construction of the Bank of England's Divisia index.
Real per capita monetary asset holdings are calculated using a superlative price index (for nondurables and services) and an estimate of the U.K. home population. Real user costs of the monetary assets are calculated as the discounted difference between the rate of return on a benchmark asset and the own-rate of the particular asset [Barnett (1978)]. Interest rates are tax-adjusted as appropriate. Nominal user costs are constructed by multiplying the real user costs by the same superlative price index that was used to convert nominal monetary asset holdings into real asset holdings.
The Bank of England constructs the benchmark rate as the upper envelope over the component rates, which include rates on Tax-Exempt Special Savings Accounts (TESSA) beginning in 1991 and Individual Savings Accounts (ISA) beginning in 1999. The upper envelope is dominated by the rate on TESSA from 1991 until 1999. It is dominated by the rate on ISA, once they are introduced; See Hancock (2005). Consequently, TESSA are treated as a monetary asset by the Bank of England from 1999:2 until 2004:1 (after which they were phased out completely). The TESSA expenditure share is, however, low and declines rapidly over this short period. To avoid testing over shorter periods with different sets of assets and to allow testing up through 2005:1, we aggregate TESSA and ISA together. We include a weighted average of their interest rates in the upper envelope with weights determined by the amounts deposited in each type of account. This aggregate rate dominates the upper envelope throughout the post-ERM period for our data.
The Bank's upper envelope also contains the rate on local government bills plus 200 basis points while they were in issuance until 1993 and the upper envelope is dominated by this rate up through 1990. Thus, user costs are based on different benchmark rates before and after TESSAs are introduced in 1991. In addition, as noted by Hancock (2005), the 200 basis point adjustment was ad hoc.
The Bank of England also switches from using quoted rates to using effective rates, when such data becomes available. Effective rates are calculated by dividing the value of interest paid by the outstanding level of balances, whereas quoted rates only reflect interest rates paid on new deposits. Hancock (2005, p. 42) argues that effective rates “are both practically and theoretically more appealing than quoted rates.” We follow the Bank of England's practice of using effective rates when possible.
Finally, from 1999, the Bank of England separates instant access accounts at building societies from accounts requiring a period of notice. We continue to treat total BSD as a single asset, however, which facilitates testing weak separability over a longer period using consistent data. When they are available, we weight together the two different reported interest rates (for instant access and notice accounts) with weights determined by the amounts deposited in each type of account.
WEAKLY SEPARABLE GROUPINGS AND DIVISIA MONETARY AGGREGATES
We test four groupings of monetary assets for weak separability. The narrowest grouping, D1, consists of NI and IBSD. The broadest grouping, D4, consists of all assets considered in our study. D3 excludes IBTD from D4 and D2 excludes BSD from D4. The four groupings are summarized in Table 1.

Barnett (1982, p. 697) argued that, in addition to being weakly separable, an admissible monetary aggregate should be nested about “hard core money,” which must include currency. In our view, the monetary aggregates should be nested about (at a minimum) all non–interest bearing assets. We chose to further include interest-bearing sight deposits in all tested groupings.
We found that the quantity and price data for all goods, services, and household sector monetary assets satisfies GARP over the post-ERM period. This implies that the data can be rationalized by a well-behaved utility function and is, therefore, consistent with utility maximization. We also tested the quantity and user cost data for the monetary asset groupings for GARP, which is a necessary condition for weak separability.
The D1 and D3 monetary asset groupings satisfy GARP. The D4 monetary asset grouping had two GARP violations, but these could be eliminated by excluding three quarterly observations from our data set (1998:4–1999:2) around the time of the change from using quoted rates to using effective rates to construct user costs. The exact dates when effective rates become available appear to differ slightly across assets, making user cost comparisons problematic over this short period. Thus, it seems defensible to exclude these observations. The D2 monetary asset grouping had 19 GARP violations. The number of GARP violations is reduced to 10 if we exclude the same three quarterly observations. The remaining GARP violations can be eliminated by removing, in addition, the first six quarters of the period.
Subsequent testing indicated that the D1 and D3 groupings are weakly separable over the entire post-ERM period. The D2 and D4 groupings both violate GARP and, therefore, weak separability. D2 is, however, found to be weakly separable over the sample period 1994:2 to 2005:1 (excluding 1998:4 to 1999:2) for which it satisfies GARP. The D4 grouping violates weak separability over the post-ERM period even if we exclude 1998:4 to 1999:2, although excluding these observations is sufficient for it to satisfy GARP. Weak separability is accepted, however, if we also exclude the first five quarters of the period.8
Specifically, we reject weak separability for D4 for 1993:4 to 2005:1 (excluding 1998:4–1999:2) using Swofford and Whitney's (1994) test, but we accept weak separability for 1994:1–2005:1.
Thus, the tests indicate that the D1 and D3 groupings are weakly separable over the entire post-ERM period. Strictly speaking, D2 and D4 violate weak separability over the post-ERM period. These violations can be eliminated, however, by removing three quarterly observations around the time of the change from using quoted rates to using effective rates and slightly shortening the sample period. To summarize, we conclude that the four groupings we consider, D1 through D4, are weakly separable over either all (D1 and D3) or almost all (D2 and D4) of the post-ERM period.
We constructed Divisia aggregates for the D1–D4 groupings using the same methods as the Bank of England, which are described in Hancock (2005). In the next two sections, we provide empirical results using these Divisia aggregates. Our D4 aggregate differs very slightly from the Bank of England's household sector Divisia index in that the latter treats TESSA as a monetary asset from 1999:2 to 2004:1. To facilitate easy replication of our empirical results, we report results for the official Bank of England index instead of for D4.
DOES NOMINAL DIVISIA MONEY CONTAIN INFORMATION ABOUT OTHER NOMINAL VARIABLES?
In this section, we estimate trivariate vector autoregressive (VAR) models comprised of log-changes in nominal Divisia money, log changes in nominal GDP, and log changes in the GDP-deflator. We then test for Granger causality of each variable against all other variables in the model. Our analysis in this section is closely based on Estrella and Mishkin's (1997) study of the United States.
We estimate the VAR over the longest sample period for which the Divisia aggregates can be constructed (1977:1–2005:1). The VAR model contains three lags of each variable to maintain consistency with Estrella and Mishkin (1997). The test results are qualitatively similar in the range of one to four lags. In most cases, results are somewhat stronger for one to two lags and slightly weaker for four lags. The significance probabilities (p-values) reported in Table 2 come from an F-test of the hypothesis that the coefficients of all of the lags of a given variable in a given equation are zero. At the 5% significance level, we find that all four Divisia aggregates aid in predicting nominal output growth, but neither nominal output growth nor inflation aid in predicting nominal money growth (irrespective of aggregation level). In addition, none of the Divisia aggregates aid in predicting inflation at reasonable significance levels, except for D1, which is significant at the 10% level. Nevertheless, the long-run coefficient on nominal D1 growth in the corresponding inflation equation is negative. In contrast, the long-run coefficients on nominal Divisia money growth in the corresponding nominal output growth equations are in the range from 0.41 for D1 to 0.70 for the Bank of England's index with D2 and D3 both being close to 0.54.9
It is possible that our results could be strengthened by considering co-integration. For example, Estrella and Mishkin (1997, p. 285) estimated a cointegration relation between velocity and a short-term market interest rate and included the first lag of the residual from this relation in the nominal growth equation of the VAR. This led to somewhat stronger results for their longer sample period but not for their shorter period. For Divisia money, one also could consider a cointegration relation involving a dual-user cost index for the monetary aggregate, which can account for the payment of interest on the monetary assets. We note, however, that the Bank of England does not publish an official dual user cost index for their household Divisia index.

We also considered the shorter post-ERM period, which was used in the weak separability analysis. Our results for this period (again with three lags) are substantially weaker than those obtained for the full sample. Specifically, only D1 is significant in the nominal income equation at the 5% level of significance, but its long-run coefficient is negative. D2 and D3 are significant at the 10% level, but D4 is not.
DOES DIVISIA MONEY HAVE DIRECT EFFECTS ON AGGREGATE DEMAND?
Nelson (2002) tested whether real monetary base growth enters into backward-looking specifications of the IS curve using U.K. and U.S. data. We extend his analysis by testing whether real Divisia money growth enters into Nelson's specification of the IS curve for the United Kingdom.
In particular, let yt be quarterly real output gap at time t, let Δ(m−p)t be the quarterly change in the logarithm of a real money measure, let Rt be a short-term quarterly nominal interest rate, and let pt be the logarithm of a price index. Nelson (2002) measures real interest rates as
, where Δ4pt = pt−pt−4, which he interprets as a smoothed version of the pseudo-real interest rate. The standard IS curve is estimated by regressing yt against four lags of itself and four lags of the real interest rate. The IS curve with money is estimated by adding four lags of real money growth to the regression.
We measure real output gap as deviations of the logarithm of real GDP (seasonally adjusted) from a quadratic trend.10
The detrending regression uses data for 1960:1–2005:1 to be consistent with Nelson (2002).
Nelson (2002) used RPIX as his price index, which is not seasonally adjusted. He removed any residual seasonality from the real money growth rate by regressing it against seasonal dummies. Results using that method are very similar to the results we report.

The estimations reveal a number of interesting findings. First, we find evidence of direct effects of both Divisia and base money in the IS relation. The first three lags of Divisia money growth (using all four aggregates) are almost all individually significant. Four lags of Divisia money growth are jointly significant based on an F-test for all Divisia aggregates. The long-run coefficients on Divisia money growth are positive and statistically significant, ranging from a low of 3.23 to a high of 3.93.12
Nelson (2002) finds values of 3.42 for the United Kingdom and 3.40 for the United States for monetary base.
A second major finding is that the long-run coefficient on the real interest rate is often positive, but is statistically insignificant in all equations. In the regression that omits all monetary variables, the long-run coefficient is 0.36, but it falls to 0.32 when base money growth is included. When Divisia money is included, the long-run coefficient is lower, ranging from 0.08 to–0.09. One finding, which is more in agreement with economic theory, is that the second lag of the real interest rate is always negative and statistically significant with a value of approximately–0.25.
Our main findings are very similar to Nelson's (2002) results for his 1982–1999 period. Most importantly, we find that real money growth enters the IS curve positively and significantly for both Divisia and base money. It is worth noting, however, that the improvement in fit from the model that omits money to the best fitting specification that includes real money growth (based on D1) is very modest–R2 improves from 0.948 to at best 0.963. This finding mirrors Nelson's results for his full sample 1961–1999 with and without monetary base in the IS-curve (he does not report results for a model that omits money for his shorter sample period).
CONCLUSIONS
The Bank of England's recently revised household sector Divisia index pays careful attention to an array of measurement and aggregation issues, but does not consider the aggregation-theoretic admissibility criteria of weak separability, which underlies Divisia aggregation. Instead, the Bank of England constructs a single index for the household sector monetary assets. Empirical research has often stressed that both the composition and construction of monetary aggregates matter for gauging their value in empirical settings [see, for examples, Swofford and Whitney (1991), Belongia (1996), and Schunk (2001)]. Moreover, the widely acknowledged theoretical superiority of the Divisia monetary aggregate rests on the property of weak separability of the components of the aggregate.
We tested various groupings of U.K. household sector monetary assets for weak separability, focusing on the recent post-ERM period. We identify four groupings of monetary assets that are weakly separable over all or almost all of the post-ERM period. We then evaluate the potential for the corresponding Divisia aggregates to be used as indicator or information variables.
First, we examined whether or not the growth rates of the nominal Divisia indexes Granger cause inflation and nominal output growth. Our results suggest that the Divisia indexes may be helpful in predicting nominal income growth, but appear to be unhelpful for predicting inflation.
Estrella and Mishkin (1997, pp. 300–301) argued that velocity (or, more generally, money demand) shocks are a form of noise that obscures the information contained in monetary aggregates, since such shocks alter the relationship between nominal money growth and other key macroeconomic variables. Thus, during periods when nominal money growth, nominal income growth, and inflation are subdued, the “signal-to-noise ratio” for the monetary aggregates is likely to be low. On the one hand, this argument may help explain why Divisia money is not very helpful in explaining inflation in our application, since UK inflation can be characterized as relatively low and stable after 1982. On the other hand, our results for nominal income growth are fairly encouraging.
Next, we found that real Divisia money growth enters positively and significantly into a backward looking specification of the IS-curve for the United Kingdom. Thus, Divisia aggregates appear to have direct effects on aggregate demand. In contrast, long-run coefficients on the real interest rate are generally not significant in the IS curve. At a minimum, these findings reinforce the claim that the short-term real interest rate fails to fully summarize the effects of monetary policy actions on the economy [Meltzer (2001)].
All in all, our findings suggest that a range of Divisia aggregates may provide additional information with respect to both nominal and real variables for the United Kingdom. In particular, our evidence lends support to the claim that Divisia monetary aggregates contain more information than short-term real interest rates with respect to the business cycle and should, therefore, be used alongside such variables in policy-relevant research. Whether or not monetary aggregates can be used in a more ambitious way, however, remains the subject of future research.
We gratefully acknowledge funding for this project from the Jan Wallander and Tom Hedelius Foundation (J03/19). Barry Jones thanks Aston University for support of this research. We thank AEM Design for allowing us to use their commercial solver FFSQP free of charge as academics [Zhou et al. (1997)]. We thank members of the European Central Bank for helpful comments made in a seminar delivered there. We thank staff of the Bank of England (in particular Matthew Hancock and Norbert Janssen) for discussing the benchmark revision of the Bank of England's Divisia index and the underlying data with us and for assisting us in interpreting and using the data. Finally, we thank the two anonymous referees whose comments and suggestions substantially improved the paper. All errors and interpretations are the responsibility of the authors.





