INTRODUCTION
Following the seminal article of Lucas (1978), increasing attention has been paid to the analysis of the stochastic behavior of equilibrium asset prices in a one-good, pure-exchange economy with identical consumers. Most of the literature relies on simulations to undertake such an analysis as a closed-form solution is usually not available for this type of problem. Closed-form solutions for the price to dividend ratio can, however, be obtained assuming either an i.i.d. rate of growth of endowment [see Abel (1990)] or a simple finite-state first-order Markov process [see, e.g., Mehra and Prescott (1985) and Cecchetti, Lam, and Mark (1993)]. More recently, Burnside (1998) has shown that exact solution to the asset pricing problem can be obtained when the rate of growth of dividends follows an autoregressive process with Gaussian shocks provided preferences are represented by a constant relative risk aversion utility function. The closed-form solution obtains because, in the case of a CRAA utility function, the marginal rate of substitution between consumption at two dates is an exponential function of the growth rate of consumption between these two dates and when the growth rate of endowment is Gaussian. Tsionas (2003) extends these results to the case of non-gaussian innovations and furnishes additional conditions for a stationary bounded equilibrium. It is, however, worth noting that all the last results obtain in the case of time-separable preferences.
In this paper, we further extend Burnside's results to the case where preferences are not time-separable, when the nonseparability stems from habit formation. Following Abel (1990, 1999), we assume that the utility function of the representative agent can be written as a power function of the ratio of current to past consumption, therefore keeping with the homogeneity assumption that allows for a closed-form solution. This paper, therefore, builds a bridge between Abel (1990) and Burnside (1998). It is, however, well known since Abel (1990) that this form of preferences does not preclude the existence of negative asset prices. In order to solve this problem, we assume that the innovations of the dividend growth process are drawn from a truncated Gaussian distribution. Hence, this paper improves on Abel (1990) in two ways: (i) we extend Abel's model to the case of serially correlated endowments and (ii) we consider a more general case in which the habit persistence parameter can take any value within its admissible range. We provide an exact solution for the price-dividend ratio and give conditions that guarantee the existence of a stationary bounded equilibrium. Note that for comparability purposes, we consider a utility function that nests the time-separable utility function of Lucas (1978) and Burnside (1998), and assume that the rate of growth of endowment follows an autoregressive process.
The paper is organized as follows. The next section presents the model. Sec- tion 2 gives the exact solution to the asset pricing model by iterating forward on the Euler equation expressed in terms of the price-dividend ratio and making use of properties of the stochastic process governing the rate of growth of dividends. In Section 3, conditions for a bounded solution are given. We also discuss the implications of habit persistence on the price-dividend ratio. A last section offers some concluding remarks.
AN ASSET PRICING MODEL WITH HABIT PERSISTENCE
We consider the problem of an infinitely lived representative agent who derives utility from consuming a single consumption good. The agent has preferences over both her current and past consumption, therefore reflecting the existence of some habit persistence phenomenon. She determines her consumption, asset holdings plans so as to maximize the expected sum of discounted future utility

where
. Ct denotes the agent's consumption of a single perishable good at date t. Et(.) denotes mathematical conditional expectations. Expectations are conditional on information available at the beginning of period t. β>0 is a subjective constant discount factor, θ>0 denotes the curvature parameter, and φ∈[0, 1] is the habit persistence parameter. When determining her consumption/asset holdings plans, the agent faces the budget constraint

where St denotes the share of the asset owned by the agent, Pt is the price of a share in period t. Dt denotes dividends, which should be thought of as the stochastic endowments paid to the owner of each unit of the asset held from period t−1 to t. The agent determines her consumption/asset holdings plans,
, maximizing her expected utility (1) subject to the budget constraint (2). The first-order condition that determines the agent's consumption choices is given by

In an equilibrium, St=1 for all t so that Ct=Dt. Then equation (3) rewrites:

EXACT SOLUTION FOR THE PRICE–DIVIDEND RATIO
Up to now, no restrictions have been placed on the stochastic process of dividends. Most of the literature assumes the rate of growth of dividends is i.i.d. and normally distributed [see, e.g., Abel (1990) and (1999), among others]. We depart from this assumption in two respects. First, following Burnside (1998), we relax the i.i.d. assumption. The growth rate of the endowment γt≡log(Dt/Dt−1) is indeed assumed to follow an AR(1) process

where |ρ|<1 and εt is an i.i.d. process. Second, we depart from the commonly adopted Gaussian distribution assumption and rather consider a truncated normal distribution, such that εt is distributed as a truncated Gaussian distribution over the support
. The latter restriction implies E(ε)=0. We further denote
. As previously noted by Abel (1990), the asset pricing model with habit persistence does not preclude the existence of negative asset prices. The possibility of negative prices comes from (i) the log–normal assumption and (ii) the marginal utility of consumption, which can be negative when the habit persistence or relative risk aversion are too large. Using the Markov chain approximation of the law of motion of γt, Abel shows that it is possible to determine the upper and lower bounds on the process that guarantee positive prices. Truncating the support of the distribution amounts to impose such a restriction provided
is not too large. Note that this assumption can be relaxed when φ=0 as the price is always positive, because the model just reduces to a time-separable model.
In order to characterize a solution for equation (4), it is convenient to rewrite the Euler equation. We first denote vt≡Pt/Dt as the price-dividend ratio. Second, we define zt≡exp((1−θ)γt−φ(1−θ)γt−1) and yt≡vt[1−βφEtzt+1]. It follows that equation (4) rewrites

Equation (5) has to be solved for yt. This forward looking stochastic difference equation admits an exact solution reported in the next proposition (see Appendix A for a proof).
PROPOSITION 1. The equilibrium price-dividend ratio is given by

where

and

and

where Φ(·) denotes the cdf of the Gaussian distribution.
Equation (6) nests many asset pricing formula. For instance, setting θ=1 (logarithmic utility function), the price-dividend ratio is constant for all states of the nature as Pt/Dt=βχ/(1−βχ). Then habit persistence does not matter for the behavior of the price-dividend ratio, as the parameter φ does not enter in the pricing formula. However, the constant term χ still distorts the price-dividend ratio, as the agents must formulate forecasts on the stream of discounted dividends using a truncated distribution. Nevertheless, as
, χ tends to 1, the price-dividend ratio tends to the usual Pt/Dt=β/(1−β).
Setting φ=0—that is, imposing time separability in preferences—we recover Burnside's (1998) solution. In this case, the price-dividend ratio rewrites:

where
and
. Once again, the truncation assumption affects the solution as long as
.
Finally, when the rate of growth of endowments is i.i.d. over time (
) and φ is set to 1, we recover the solution used by Abel (1990) to compute unconditional expected returns (see Abel (1990), Table 1, panel C, p. 41):

with
. In this latter case, as equation (7) makes it clear, the price-dividend ratio is an increasing (resp. decreasing) and convex function of consumption growth if θ>1 (resp. θ<1). In other words, only the position of the curvature parameter around unity matters.
DISCUSSION
Note that the solution for the price-dividend ratio involves a series, which convergence properties have not been yet discussed. The following proposition determines a necessary and sufficient condition for the existence of a stationary bounded equilibrium (see Appendix B for a proof).
PROPOSITION 2. The series in (6) converges if and only if

This proposition makes clear that as in Burnside (1998), β<1 is neither necessary nor sufficient to insure finite asset prices. Moreover, it shows that habit persistence help guaranteing a bounded solution. For instance, let us focus on the case θ>1 and first consider the time separable case (φ=0). If the future path of endowment is uncertain, risk adverse consumers (θ very large) are willing to purchase a large amount of assets today to insure themselves against future bad outcomes—that is, the series goes to infinity. Conversely, when habit persistence is strong enough (large φ), the solution is bounded as the effect of uncertainty is lowered by the smoother consumption path, even for large value of θ. In the limiting case where φ=1, the price-dividend ratio takes the form of equation (7) and therefore the series drops out as the forecasting horizon reduces to one period ahead. Other- wise stated, discounted future risk would be inconsequential. Also note that truncation of the distribution makes conditions for boundedness less demanding as a lower
reduces the overall volatility of dividends and therefore reduces risk. Households are therefore less willing to purchase assets, which puts downward pressure on asset prices.
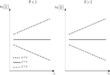
Endowed with conditions for boundedness, we are now in a position to discuss the form of the solution. Let us consider the general model, where endowments are serially correlated (|ρ|[les ]1) and φ is not restricted to either 0 or 1 [see Abel (1990)]. In this case, as can be seen from the form of parameter bi, both the position of the curvature parameter, θ, around 1 and the position of the habit persistence parameter, φ, around ρ matter. This is illustrated in Figure 1, which reports the price-dividend ratio as a function of dividend growth for different values for φ.

Price–dividend ratio Pt/Dt.
As can be seen from the figure, when θ>1 (resp. θ<1), the decision rule is increasing (resp. decreasing) with dividend growth when φ>ρ (resp. φ<ρ). The economic intuition underlying this result is clear. Let us consider the case θ>1 A shock on dividends exerts three effects: (i) a standard wealth effect, (ii) a stochastic discount factor effect, and (iii) a habit persistence effect. The two latter effects play in opposite direction on intertemporal substitution. When φ>ρ, the stochastic discount factor effect is dominated by the force of habits, as the shock on dividend growth exhibits less persistence than habits. Therefore, the second and the third effects partially offset each other and the wealth effect plays a greater role. The price-dividend ratio increases. Conversely, when φ<ρ habit persistence cannot counter the effects of expected stochastic discounting, and intertemporal substitution motives take the upper hand. The price-dividend ratio decreases. Note that in the limiting case where ρ=φ (plain dark line in Figure 1) the persistence of dividend growth exactly offsets the effects of habit persistence and all three effects cancel out. Therefore, just alike the case of a logarithmic utility function, the price–dividend ratio is constant. The reasoning is reversed when θ<1 (see left panel of Figure 1).
A final remark regards the numerical accuracy of the solution. Indeed, although we have a closed-form solution, it involves an infinite series that cannot be exactly computed as it requires truncation. Nevertheless, we can determine the truncation breakpoint that yields an arbitrarily small error. Let us focus on the infinite series and denote the truncated series at horizon K by SK, such that
. One way to determine a truncation point is to select K such that P(ΔSK[ges ]δ)[les ]η where ΔSK=SK−SK−1 and δ, η>0. Since
, Markov's inequality implies that

It is then easy to select K such that
, where δ may be given by machine precision and η a low enough probability.
CONCLUDING REMARKS
This paper offers an exact solution for the price-dividend ratio in a standard asset pricing model with (i) an autoregressive process for the endowments with a truncated Gaussian distribution of innovations and (ii) habit formation, therefore extending Abel's (1990) and Burnside's (1998) results. We establish conditions under which the solution is bounded and give some restrictions on the parameters to guarantee positive asset prices, and a practical way of determining an accurate numerical evaluation of the closed-form solution.
APPENDIX
A PROOF OF PROPOSITION 1
Iterating forward, and imposing the transversality condition, a solution to this forward looking stochastic difference equation (5) is given by

Note that, from the definition of zt, we have

Since γt follows an AR(1) process, we have
. This implies that

and

Furthermore, because we assumed that dividend growth is normally distributed, we can make use of standard results on truncated log–normal distributions, to compute

where
,
and

with Φ(·) is the cdf of a gaussian distribution.
Using (A.1) and (A.2), the first term is simply given by
. The calculation of
requires more algebra

Likewise,
. Therefore, the solution to (5) is given by

where

Recalling that yt=vt[1−βφEtzt+1] and making use of the calculation of Etzt+1, we finally get the price to dividend ratio. This completes the proof.
B PROOF OF PROPOSITION 2
Let us define

where ai and bi are defined in the main text. Then the series in vt may be written as

It follows that

where

Then, provided |ρ|<1, we have

Therefore

Using the ratio test, we now face three situations:
- When r<1, then and the ratio test implies that converges.
- When r>1, the ratio test implies that diverges.
- When r=1, the ratio test is inconclusive. But, if r=1, we know that

and the parameter ai rewrites

After replacement in wi, we get:

where

Since
, the series
diverges.
Therefore, r<1 is the only situation in which a stationary bounded equilibrium exists.
This paper has benefited from discussions at the T2M Conference (Orléans, January 2004). We also would like to thank K.E. Beaubrun-Diant, J. Matheron, William A. Barnett, and two anonymous referees for helpful comments. The traditional disclaimer applies.