INTRODUCTION
Milton Friedman devoted an important part of his outstanding career looking at the contribution of government policies to business cycle fluctuations. He asked many relevant questions: Under what conditions will policies contribute to reduce business cycle fluctuations? Can vigorous countercyclical policy lead to instability? Should medium-term goals, such as price stability, be given primacy? He also questioned what policy might, realistically, achieve by stressing what policy cannot feasibly do. The limits to policy stem from long and variable lags in transmission, from endogenous expectations on the part of households and firms, and from imperfect knowledge on the part of policy makers about the structure, current state, and prospects for the economy. Today's lecture will revisit some questions within Friedman's research program.
The title of this lecture is “Monetary Policy over Time.” It may be understood as relating to a number of very different questions:
How have monetary policy regimes evolved historically?
How does the profile of monetary policy action look like in response to relevant economic disturbances (demand shocks, supply shocks, cost-push shocks and so on)?
How does the adjustment look like in the event of a change in the policy regime?
In this lecture, we will have the opportunity to cover some limited aspects of all three questions. On the first, we will limit ourselves to some comments on the Great Inflation of the 1970s, and the early 1980s, and the subsequent disinflation. The second and the third questions will provide the main focus for the lecture. Friedman (1968) provides a natural starting point. In this paper, Friedman criticised the interpretation of the Phillips curve (Phillips, 1958) as providing a permanent and exploitable tradeoff between inflation and unemployment. He states: “… there is always a temporary trade-off between inflation and unemployment; there is no permanent trade-off. The temporary trade-off comes not from inflation per se but from unanticipated inflation, which generally means from a rising rate of inflation.” In Friedman's view, there is a temporary tradeoff only because expectations are slow to adjust. However, because people will not make systematic mistakes forever, there cannot be a permanent tradeoff.
Friedman did not formalize expectation formation explicitly. However, the natural rate hypothesis provided fertile ground to apply the rational expectations approach of John Muth (Muth, 1961). Rational expectations are fully model-consistent. Formally, rational expectations are defined as the mathematical conditional expectation of the relevant variables. They do respect a number of very desirable properties that any endogenous expectation mechanism must fulfil. They imply that agents do take into account all relevant information at their disposal and do not make systematic mistakes. Assuming that firms and households make systematic mistakes, and refuse to learn from experience, does not look like an attractive alternative.
The rational expectations revolution in macroeconomics had deep implications for our understanding of policy making. Kydland and Prescott (1977) pointed to a very important tension between optimal and consistent policy over time. Specifically, they show that, in their inflation-unemployment example, that the time-consistent policy maker will not take the effects of future policies on private sector expectations into account. In doing so, she ignores the endogeneity of private sector expectations and departs from optimal policy. In the example, the time-consistent policy is dominated by a simple rule requiring the central bank to deliver price stability. The recognition of the importance of private sector's expectations led to increased emphasis on the concepts of credibility and reputation. Barro and Gordon (1983a, 1983b) used time-consistency to identify the possibility of an “inflation bias.” They argue that such bias could explain the “Great Inflation” that occurred after the demise of Bretton Woods, and the transition to fiduciary monetary regimes around the world.
The relevance of the “inflation bias” to explain the behavior of actual policy makers is controversial. Recently, many authors have emphasized the importance of the profile of monetary policy actions over time, under rational expectations, even disregarding inflation bias [see, for example, Clarida, Gali, and Gertler (1999) and Woodford (2003)]. Facing a shock inducing a tradeoff between price stability and output gap stability, the policy decision maker may, by credibly committing to a persistent policy response, reduce the initial impact of the shock, thereby spreading its impact over time. A regime characterized by such a policy rule generates expectations, which act as automatic stabilisers, mitigating the impact of economic disturbances. One question addressed in the current paper is whether and how intertemporal effects of policy making play a role when private sector agents depart from rational expectations.
Specifically, we follow Marcet and Sargent (1989) and Evans and Honkapohja (1998, 2001). They have explored a new view, on expectation formation, and labeled it adaptive learning. The idea is that households and firms revise their views on the economy with new data. They are “bounded rational” à la Sargent (1993) and, under favorable conditions, their beliefs converge to rational expectations. In this lecture, we will explore implications of departures from rational expectations in the direction of a specific example of adaptive learning. There is a growing literature exploring the implications of adaptive learning for the conduct of monetary policy.1
It includes, among others, Orphanides (2001, 2002, 2003), Orphanides and Williams (2002a, 2003c, 2003d), and Bullard and Mitra (2002).
A very relevant example is policy regime change. Change in the policy regime, which generates policy actions over time, would, under rational expectations, be anticipated by the private sector. Therefore, a policy maker relying on a macroeconometric model estimated by a competent econometrician, based on historical data, will be dismayed and frustrated by systematic and persistent deviations between outturns and model forecasts. In his original paper, Lucas (1976) explored a number of examples under rational expectations. He conjectured that there was no reason to believe that the structure of a macroeconometric model would be invariant even if the expectation formation process would depart from rational expectations.
McCallum (2005) has argued that the instantaneous adjustment of expectations to a regime change implied by rational expectations is unreasonable. Moreover, there is some tension in the rational expectations account of regime change. The new regime is assumed completely unanticipated ex ante and perfectly credible ex post. Typically, rational expectations assume a seamless transition between two perfectly credible policy regimes. Regime change itself is never anticipated. Adaptive learning may provide a better approach to modeling the transition dynamics of regime change. In this lecture, we will assume adaptive learning to model regime change.
The purpose of this lecture is to look at the implications, for the conduct of monetary policy over time, assuming endogenous private sector expectations, according to adaptive learning. We will consider the simplest possible new Keynesian model with sticky prices and endogenous persistence [see, for example, Clarida, Gali, and Gertler (1999) and Woodford (2003)]. We will completely abstract from the monetary transmission mechanism and simply assume that the central bank controls inflation by means of the output gap. This lecture is organized as follows: in Section 2, we introduce the model and characterise the optimal policy under discretion and commitment under rational expectations. Optimal policy under commitment shows a high degree of persistence over time.
In Section 3, we consider the implications associated with assuming adaptive learning dynamics, on the side of the private sector. We contrast two cases. In the first, a naïve policy maker simply follows the first-order condition derived for optimal policy under discretion and rational expectations. In the alternative case, the central banker is assumed to know everything. She even knows that private sector expectations are endogenous and follow an equation generated by a learning algorithm. Because agents are backward-looking, announcements don't matter. Actions do. The sophisticated CB recognizes that policy actions affect not only current outcomes but also the future environment through the slowly moving expectations formation process. We will investigate questions such as: Are policy actions persistent under learning? How do differences between naïve and sophisticated policy under learning compare with differences between discretion and commitment under rational expectations? How well anchored is the inflation process under the various alternatives?
In Section 4, we will discuss issues of regime transition under learning. Specifically, we will want to look at the transition from a naïve regime that has been found to be unstable to a sophisticated regime. How will the sophisticated CB go about anchoring back the inflation process? How long will it take for the learning equation to come back? How are policy actions and macroeconomic outcomes characterized in the transition? We will use the insights from our simulations to look at the regime change in monetary policy making, in the United States, after October 1979. In order to revisit the taming of inflation, by Paul Volckers's Fed, we will heavily rely on the fascinating account recently made available by Lindsey, Orphanides, and Rasche (2005). We will argue that our model helps to rationalize a number of important features of the Great Inflation and the subsequent long adjustment toward price stability.
Section 5 will conclude.
A SIMPLE MODEL: OPTIMAL POLICY UNDER RATIONAL EXPECTATIONS
In this section, we use a very simple model of inflation dynamics and analyze the optimal policy response under rational expectations.
The model is consistent with the following microeconomic assumptions. Producers set prices in an environment of nominal rigidity, formalized using the Calvo (1983) shortcut. That is, in a given period, a specific firm will be “allowed” to reset its price optimally with an exogenous and constant probability. Firms produce using a technology that exhibits decreasing returns to labor. Furthermore, preferences of Dixit and Stiglitz (1977) type introduce monopolistic competition, with a continuum of otherwise identical firms. Finally, output is assumed to be demand determined, which means that firms will sell whatever quantity demanded at its current price. These four assumptions create a role for monetary policy, as without intervention markets may produce inefficiently. A simple way to see that this is the case is to note that as all firms are symmetric and marginal cost is increasing in production, the optimal allocation will be such that all firms have the same level of output. However, with some prices fixed, this will typically not be the case. Optimal monetary policy will strive to equalize relative prices of firms of the two groups, to avoid dispersion in the output distribution. The features described so far are almost always present in new Keynesian models.
In order to examine the issues we are interested in, we introduce two further components. First, motivated by the empirical fact that inflation is relatively persistent, we introduce indexation to lagged inflation among the firms, which do not reset their price optimally along the lines of Christiano et al. (2005) and Smets and Wouters (2003). In this case, current inflation will have two components, one coming from the optimally reset prices (the only component in the standard framework) and one a result of all other prices change in proportion to lagged inflation. This assumption has the pleasant by-product of reducing the extreme dispersion of prices that may otherwise surface (in the standard Calvo framework, there will be a positive measure of firms that have never changed their prices during the last x periods, with x arbitrary).
Second, we assume that there is a temporary cost-push shock that affects inflation. In terms of microeconomics, this can be motivated by a stochastic intratemporal elasticity of substitution between goods, as in Steinsson (2003), leading to a time-varying markup on marginal cost. We introduce this feature as a short cut to get a tradeoff for optimal monetary policy, which otherwise will be trivial under the perfect information assumption.
In terms of equations, Woodford (2003) shows that these assumptions implies a Phillips curve of the form

where π is inflation, x is the output-gap, u is the cost-push shock and ω=(1+βγ)−1. Furthermore, the loss function (which is, up to a second-order approximation, the negative of the social welfare function consistent with the micro foundations) is of the form

We assume that the central bank uses (2) to guide its policy decisions.
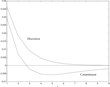
We start by solving for the rational expectations equilibrium under both discretion and commitment using standard methods. Figures 1 and 2 show the impulse responses of inflation and the output-gap, under discretion and commitment in response to a positive (one-off) cost-push shock. It is interesting to note that, under discretion, the output gap moves only at the time of the shock. Monetary policy tightens on impact and immediately returns to normal. In contrast, the commitment response displays a clear inertial character. Monetary policy tightens on impact and stays tight for a while, allowing output to return to potential only gradually.

Inflation response to a cost-push shock, rational expectations.

Output response to a cost-push shock, rational expectations.
Figures 1 and 2 illustrate the time-consistency problem of the optimal policy under commitment. The point is clear-looking at any period after the first. In fact, from the second period onward inflation is below target (here assumed to be zero) and output is below potential. It seems clear that policy should be expansionary. Why is the inertial response optimal? By committing to a gradual and persistent response to cost-push shocks the central bank is able to mitigate the initial impact of cost-push shocks and to spread their impact over time. Figure 1 shows that, under commitment, inflation actually undershoots the inflation target. The reason for undershooting is the favorable impact it has on current price setting. Woodford (2003) interprets the dependence of current policy on past shocks as “history dependence.” The path of the inflation response under commitment resembles what would be expected under a price-level targeting regime. Finally, it is also clear from Figures 1 and 2 that inflation comes down significantly quicker under commitment than under discretion. In contrast, the output gap in much more persistent under commitment. Clarida, Gali, and Gertler (1999) interpret this discrepancy as a stabilization bias under discretion. Notice that the formulation we have adopted for the policy problem, in particular the absence of an overambitious output target, ensures the absence of an “inflation level bias.”
INTRODUCING LEARNING DYNAMICS: NAÏVE VERSUS SOPHISTICATED CENTRAL BANKING
We now consider how the behavior of the economy changes when the rational expectations assumption is replaced by the assumption that expectations are formed on the basis of a “constant gain” least squares algorithm implying perpetual learning.
We assume (following Gaspar and Smets, 2002) that agents use lagged information to update their parameters and form their expectations. Such simplifying assumption avoids simultaneity of current inflation and inflation expectations. Specifically, the agents estimate the following reduced form equation for inflation,

The sense in which agents are bounded rational is that they do not take into account the fact that the parameter c varies over time in an optimal way. That is, assuming that the agents know the structure of the model, they could instead use a Kalman filter to optimally update their perception of the persistence parameter. However, as lagged inflation and the cost-push shock are the only two state-variables, this specification is in fact consistent with the rational expectations equilibrium under discretion. Hence, it is not the case that agents are using an arbitrary forecasting model. In fact, one way of thinking about the behavior of the private sectors in terms of robustness. Many different structural models are consistent with the same reduced form (with possibly different parameter values). Hence, basing the forecast of inflation on a reduced form model is one way to hedge against relying on an incorrect structural model, even though it is less efficient in case one happens to know the correct model.
To be able to formulate the optimal policy problem in a recursive form, we note that the following equations describe the recursive updating of the parameters estimated by the private sector.
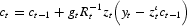

where c is the vector of estimated parameters, R is the moment matrix, y is the explained variable, z is the vector of explanatory variables and g is the gain.
In our case, we assume that the gain is constant, gt=φ. The lagged information assumption means that yt=πt−1 and that zt=πt−2. It is important to note that because of the learning dynamics, the number of state variables is now expanded to four: (ut, πt−1, Rt, ct), where we note that the last two variables are predetermined and known by the central bank at the time they set policy at time t. We further note that there are two reasons for considering the constant gain case. The first is that it is only with this case that there will be permanent action coming from the learning algorithm. In case the gain is 1/t, which corresponds to agents running an OLS regression with an increasing sample length, the estimated parameter will converge to a constant. Transition regimes could still be studied, but there would be the additional problem that the value function would not be time invariant. This problem could likely be addressed by treating time as an extra state variable, but we do not want to enter into these complications and therefore focus on the constant gain case.
All of this implies that inflation expectations, in period t, for period t+1 may be written simply as:

which may be used in (1), the standard new-keynesian Phillips curve to obtain:
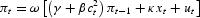
We want to contrast two cases. In the first, the central banker perceives no influence of his policy actions on inflation expectations and on the way they are formed. Specifically, we assume that the central banker uses a rule for the control variable, in our case the output gap x, that is derived from the optimal policy under discretion and rational expectations. For this case, which we label naïve central banking, the timing is as follows: in the beginning of the period, agents update their parameter estimates. Then they form their expectations. The shock is realized and observed by the central bank. The central bank chooses policy in accordance with the discretionary, rational expectations rule, which maximizes (2). Finally, inflation is realised [the algorithm is described in detail in Gaspar, Smets, and Vestin (2005)].
The alternative case is that of sophisticated (optimal) central banking. In this case, the central banker is well aware that policy actions influence expectations formation and thereby inflation dynamics. The central bank is assumed to know the expectation formation mechanism in full. We may therefore look at sophisticated central banking as implying behavior that mimics the solution of an optimal control (dynamic optimization) problem.
Specifically, it is as if the central bank would solve:

subject to the expectations adjusted Phillips curve (7) and the recursive parameter updating equations (4) and (5).
We note that the presence of learning instead of fully rational agents introduces three modifications relative to the standard framework. First, the agents simply run their regression and make their forecast, so that actual inflation is not the outcome of a game between the central bank and the private sector. Second, promises of future policy play no role as agents look only at inflation outcomes. Hence, there is no scope for the type of commitment gains discussed in Section 2. Third, we leave the linear-quadratic world, as the learning algorithm makes the model nonlinear.
From a technical perspective, the first two aspects simplify finding the optimal policy, whereas the third is a substantial complication. The problem is that the value function will not be linear-quadratic in the states and hence we have to resort to nonlinear methods in order to solve the policy problem. We therefore employ the collocation methods described in Judd (1998) and Miranda and Fackler (2002), which amount to approximating the value function with a combination of nonlinear polynomials, which translates the problem to a root-finding exercise [the details of the numerical solution method are explained in Gaspar, Smets, and Vestin (2005)].
In the simulations, we are going to assume the same parameters used for the case with rational expectations. Specifically:

Before presenting results, we want to argue that the learning algorithm we have assumed is a reasonable one. In order to do so, we note that, under recursive learning, the model eventually converges to the rational expectations equilibrium, under discretion.
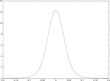
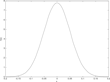
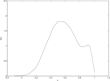
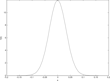
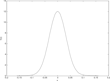
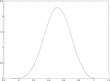
For the two cases of naïve and sophisticated central banking, Figures 3–8 show three sets of results. Figures 3 and 6 show the distribution of the persistence parameter. Figures 4 and 7 shows the distribution of inflation and Figures 5 and 8 shows the distribution of the output gap. Figures 3–5 deal with the naïve case and 6–8 the optimal policy case.

Distribution of inflation (naïve central banker).

Distribution of the output gap (naïve central banker).

Distribution of perceived inflation persistence (naïve central banker).

Distribution of inflation (sophisticated central banker).

Distribution of the output gap (sophisticated central banker).

Distribution of the perceived inflation persistence (sophisticated central banker).
Outcomes under sophisticated (optimal) central banking are better in terms of inflation (compare Figure 3 and Figure 6). Volatility of the output gap is also reduced under sophisticated central banking (compare Figure 4 and Figure 7). The result is somewhat analogous to what obtains when we compare the results under commitment and discretion in the case of rational expectations. Specifically, we see that taking explicitly into account the effects of policy over time allows for an improvement of economic performance along the relevant dimensions. There is one complication in interpreting these results, which is related to the lagged information assumption. Expectations react less strongly with this assumption, which would have an implication on the policy conducted under rational expectations if this assumption was imposed also for that case. Hence, our discretionary central banker will have a tendency to react more strongly to inflationary shocks. This reinforces the conclusion from the results related to inflation, as the dispersion there would be larger if we adjusted for this fact. However, it works in the other direction for the case of output, so that result must be considered with caution.
Under rational expectations, as argued earlier, commitment allows the central banker to use the future course of policy to spread the impact of economic shocks over time. As we have seen, in Section 2 the mechanism may be interpreted as a form of automatic stabilization. The central bank, by committing to a persistent response to a cost-push shock, induces an undershooting inflation. Under rational expectations, it brings inflation anticipations down thereby mitigating the impact of the shock.
Under adaptive learning the mechanism must be different as future policy as such plays no role at all. The intuition may be grasped from Figures 5 and 8. Under sophisticated central banking, the distribution, of perceived persistence, has lower mean (and mode) and lower variance. Moreover, and most important, sophisticated central banking avoids the right asymmetry of the distribution, and the substantial probability mass, for perceived inflation persistence just below one, which is clearly apparent from Figure 5. Therefore, inflation and inflation expectations are much better anchored under sophisticated (optimal) central banking.
Furthermore, Figure 9 shows the mean dynamic responses (the equivalent of impulse responses in a nonlinear model) of inflation and the output gap when the learning coefficient is around its normal (steady state) level of about 0.5. The top panels show the naïve case and the lower panels the optimal policy. Here we see that there is a tendency for the optimal policy to be persistent in the response to shocks, but that the response of inflation is not much different in the two cases.

Mean dynamics (perceived inflation persistence at steady state).
Figures 10 (naïve) and 11 (optimal policy) show the corresponding responses when the persistence parameter is relatively high around 0.75. Here we note that the optimal policy responds more aggressively and in a much more prolonged fashion with the associated effect that inflation does come down more quickly in this case. Perhaps the most interesting aspect to note that the persistence parameter comes down (after increasing from its central values) much faster under optimal policy, an indication that taking explicit account of the endogenous character expectations seriously is important, to avoid entrenchment of inflation persistence.

Mean dynamics under naïve central banking.

Mean dynamics under sophisticated central banking.
Hence, as in the case of commitment, the result is achieved through a persistent response to cost-push shocks. Such response offsets the adverse effects of cost-push shocks on inflation expectations and on the expectation formation mechanism. It is interesting to note that as the persistence coefficient increases, optimal policy becomes more and more inertial.
One interpretation of the results is that when the coefficient is getting out of control, optimal policy wants to bring it back. The way it does that is to generate a sequence of negative forecast errors, that is, deliver inflation rates below the private sector expectations, which through the recursive learning equations leads to a decrease in the estimated persistence.
In the preceding comments, we have abstracted from a very important feature of the model in the case of naïve central banking. The interaction of naïve central banking with adaptive learning dynamics gives rise to potential explosive dynamics when perceived inflation persistence goes to unity.2
Similar results for the case of a Taylor rule are reported by Orphanides and Williams (2004).
In Section 4, we will explicitly look at an explosive path and how it can be controlled when sophisticated central banking takes over from naïve central banking.
TAMING INFLATION: EXPLOSIVE DYNAMICS AND THE TRANSITION TO SOPHISTICATED CENTRAL BANKING
We have seen in Section 3 that the model maybe unstable under naïve central banking. In Section 3, following Orphanides and Williams (2004), we truncated the process in order to be able to exhibit the long-run distribution of perceived inflation persistence, inflation, and the output gap. Such procedure leads, naturally, to underestimates of the potential instability associated with disregarding the long-run primacy of price stability (and of expectations anchored on price stability). In this section, we want to look at one example of an unstable, explosive path and how it unfolds. Because such development would, eventually, prove unsustainable we argue that it provides a natural way to look at a regime change. Indeed, as it becomes increasingly clear that the economy is embarking on an unsustainable, unstable path it becomes increasingly clear that a regime change is necessary in order to anchor inflation and inflation expectations. Specifically, we will look at the dynamics following the transition from naïve central banking to sophisticated (optimal) central banking.
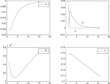
Figures 12 and 13 portray, respectively, the time path of the inflation rate, πt, and of the perceived inflation persistence parameter, ct. The figures show that naïve central banking may prove compatible with stability for a long period of time. However, eventually, a sufficiently long string of cost-push shocks will push the estimated persistence parameter close to and finally above one. When ct goes above one, the path for the economy explodes rapidly with the inflation process basically feeding on itself. Shocks are now significantly magnified through their impact on expectations. This, in turn, contributes to perpetuate inflation. Failing to recognize the importance and endogenous response of inflation expectations, the naïve central banker is unable to stop the process.3
Our model is fully simmetrical. It is as likely to get an inflation escape as it is to get a deflation escape. Given our assumptions, the two possibilities are like mirror images.

Inflation with and without regime change.

Estimated inflation persistence and regime change.
Such an explosive process will necessarily lead—at some point in time—to the realization that regime change is necessary, unavoidable, and desirable. Many alternative regimes can be imagined. We will assume that the change will take the form of a transition to sophisticated (optimal) central banking. Our assumption will allow us to use the framework discussed in Section 3. Figures 12 and 13 also portray the dynamics for the case sophisticated central banking takes over just at the moment when the perceived inflation persistence parameter is about to go above unity. After the regime change, the perceived persistence parameter and inflation are brought under control.
Figure 14 shows the response of the output gap under the two alternative regimes, just after the date of the hypothetical regime change. In such circumstances, output is much lower under optimal policy. Optimal policy deliberately opens a significant output gap in order to anchor inflation and inflation expectations. It does so by surprising the private sector with inflation consistently lower than expected. After a long transition, the path of the output gap and the alternative policies is no longer visible. In the fullness of time, we know from Section 3 that optimal (sophisticated) central banking leads to lower inflation and output gap volatility. It is so even when the explosive escapes are excluded.

Regime change and the output gap.
How does our very simple story compare with the buildup of the Great Inflation from the late 1960s until October 1979 and the subsequent Volcker disinflation? To look at this question, we rely on the account of the episode given in Lindsey, Orphanides, and Rasche (2005). The sample of texts reproduced below represents our own selection and does not aim to present a complete and balanced historical account of this important episode in U.S. monetary history.4
Such an account and relevant references are available in Lindsey, Orphanides, and Rasche (2005). All texts quoted in the remainder of this section are also quoted in their paper.
Wider recognition of the limits on the ability of demand management to keep the economy at a steady full employment path, especially when expectations are hypersensitive to the threat of more inflation, provides a more realistic point for policy formulation. So do the increasing, and in my mind well justified, concerns with the problem of inflation by the national administration and the citizenry.
Quoting from the transcripts from the 1979 meetings of the FOMC. These transcripts have only recently been made available. See Lindsey, Orphanides, and Rasche, 2005.
When I look at the past year or two I am impressed myself by an intangible: the degree to which inflation psychology has really changed…. [I]t would be very nice if in some sense we could restore our own credentials and [the credibility] of economic policy in general on the inflation issue.
…on the price front expectations have certainly gotten worse rather than better…. I certainly conclude from all this that we can't walk away today without a program that is strong in fact and perceived as strong in terms of dealing with the situation…. [W]e are not dealing with a stable psychological or stable expectational situation by any means.6
Chairman Volcker's emphasis on stable inflation expectations is so strong that it provides the basis for his definition of price stability. Indeed, in his address to the American Economic Association, in December 1983, he proposed the following definition of price stability:
“A workable definition of reasonable “price stability” would seem to me to be a situation in which expectations of generally rising (or falling) prices over a considerable period are not a pervasive influence on economic and financial behavior.”
A similar approach has been followed by Alan Greenspan, who stated that price stability could be said to exist when:
“Price levels (… are …) sufficiently stable, so that expectations of change do not become major factors in key economic decisions.”
Alan Greenspan, in a statement before the Committee on Finance, U.S. Senate, January 26, 1989.
I think in general you know the background of these actions; the inflation rate has been moving at an excessive rate and the fact that inflation and the anticipations of inflation have been unsettling to markets both at home and abroad. That unsettlement in itself and its reflection in some commodity markets is, I think, contrary to the basic objective of an orderly development of economic activity.
An entire generation of young adults has grown up since the mid-1960s knowing only inflation, indeed an inflation that seemed to accelerate inexorably. In the circumstances, it is hardly surprising that many citizens have begun to wonder whether it is realistic to anticipate a return to general price stability and have begun to change their behaviour accordingly. Inflation feeds in part on itself. So part of the job to a more stable and more productive economy must be to break the grip of inflation expectations. […] Over a longer period of time, the uncertainties and distortions inherent in inflation have a debilitating influence on investment, productivity and growth.
February 19, 1980, Paul Volcker's statement before the committee on banking, finance, and urban Affairs.
… dealing with inflation has properly been elevated to a position of highest national priority. Success will require that policy be consistently and persistently oriented to that end. Vacillation and procrastination, out of fears of recession or otherwise, would run grave risks. Amid the present uncertainties, stimulative policies could well be misdirected in the short run. More importantly far from assuring more growth over time, by aggravating the inflation process and psychology, they would threaten more instability and unemployment.
- A long history of inflation leads to a revision of the expectation formation mechanism. There is a substantial risk that inflation will feed on itself.
- Unhinged inflation expectations are a threat to economic stability in general.
- In order to anchor inflation and inflation expectations a change in policy regime is required. A continuation of past policies is unlikely to work under such circumstances (in the model it would not work at all).
- It is crucial to accept the short-run costs—in terms of output below potential—in order to restore stability and to be able to reap the long-run benefits, associated with price stability, for real economic variables.
There are two further points that may be made using historical hindsight:
- The process was far from instantaneous. It took several years for long-term interest rates, inflation, and inflation expectations to converge to levels compatible with price stability.8
Milton Friedman (1968) quoted Irving Fisher as showing that inflation expectations are slow to develop and slow to disappear. He conjectures that it may take a couple of decades for the new equilibrium to be reached.
- The recent performance of the U.S. economy in terms of inflation and output growth and volatility has been remarkable.
We do not claim that our simple model provides a complete account of the Great Inflation period and the subsequent regime change. Nevertheless, we want to stress that our model matches many aspects of this historical episode.
CONCLUSIONS
Progress in stochastic macroeconomic modeling and stochastic simulation makes revisiting the research program on macroeconomic stability and stabilization policy an exciting prospect. In this paper, we have shown that adaptive learning induces nonlinear dynamics implying stark departures from certainty equivalence.
In our examples, departures from rational expectations increase the likelihood of explosive behavior. In a sense, rational expectations impose so much discipline that (conditional on the existence of equilibrium) short-run departures, from a stability oriented course, have limited consequences. Under rational expectations short-lived policy mistakes are, to a certain extent, forgiven.
There is some analogy between the behavior of optimal policy under commitment (and rational expectations) and sophisticated (optimal) central banking under adaptive learning. In fact, under adaptive learning, sophisticated central banking implies a persistent policy response when inflation expectations threaten to become unhinged. Such policy response helps to anchor inflation and inflation expectations contributing to greater overall stability of inflation and economic activity. Stability comes, in part, through insurance against explosive dynamics.
Adaptive learning implies protracted adjustment dynamics in the event of a regime change. The dynamic behavior of the economy, in our simulations, is not unlike the behavior of the U.S. economy around the Volcker transition (October 1979). Irving Fisher would not have been surprised. In his Theory of Interest, he documented both the long lags in the adjustment of inflation expectations and the sensitivity (endogeneity) of their behavior relative to economic conditions. Specifically, he showed that in times of sharp changes in the price level, the adjustment became much faster.
The experience of the last 40 years suggests that independent central banks, with a mandate to ensure price stability, provide insurance against runaway inflation or deflation. Naïve central banking with a short-run horizon may deliver reasonable results for a long while. It leaves the economy vulnerable to a string of unfavorable cost-push shocks. Our story of naïve central banking illustrates the wisdom of Machiavelli when he wrote: “For when men have little virtue fortune shows its power very much.”9
Niccolò Machiavelli (1996), Book II, 31.5, p. 202.
The views expressed are the authors' own and do not necessarily reflect those of the ECB, Banco de Portugal, or the Eurosystem. The authors are indebted to Klaus Adam, Athanasios Orphanides, and John Williams for helpful discussions. William Barnett provided the necessary incentives for working on this Lecture.