INTRODUCTION
This paper examines the dynamic effects of international commodity trade by merging two benchmark environments, namely, the static factor endowments model and the neoclassical growth model. The central modification of the static trade model is thus a simple one: one of the factor endowments, physical capital, is permitted to accumulate over time rather than remain fixed in each of two trading countries. With this modification, the concept of relative factor abundance becomes an endogenous, rather than exogenous, feature that is reflective of national savings characteristics and potentially time variant. The main questions asked in the context of this hybrid model are then the natural ones. First, how does commodity trade affect the capital-accumulation paths of two trade partners? Second, do the welfare effects associated with these dynamics serve to reinforce or mitigate the well-known welfare effects associated with the static factor endowments model? Although these questions could not be more straightforward, it may be surprising to realize that equally straightforward answers are not yet part of the trade literature.
A positive connection between openness and economic growth via capital accumulation, if legitimate, is analogous to a prescription for economic development. It is in this practical sense that this study finds underlying importance. Additionally, although the static factor endowments model has long affirmed a positive connection between trade and welfare, it has in fact left as an open question the role that such trade may have for growth and development. Thus, there is also a theoretical gap toward which this study is directed. Moreover, in the absence of such a theory, conjectures abound as to the dynamic implications of commodity trade. It is not infrequent, however, to hear the presumption that these effects are not only positive but also are more significant than the initial, or static, effects. On all of these grounds, a growth-modified version of the factor endowments model could be illuminating.
To be more precise about the relation of this paper to the static trade model on which it is based, the latter is first briefly reviewed. Factor endowment trade theory describes the welfare effects of commodity trade for two large countries that differ from one another only with respect to their fixed endowments of the two productive factors. A pair of results that comprise the traditional welfare, or gains from trade, arguments are well established. The first and most notable result is that trade is mutually advantageous for the partnered countries. The second result, a caveat to the first, is that the gains from trade are unevenly distributed within each country. Thus, within each country engaged in trade there are distinct winners and losers. To sum, the static model concludes that the introduction of free commodity trade generates conflict within but not across countries. It is the robustness of this insight in the presence of trade-induced changes in growth that is to be explored in the model presented.1
Of course, the gains from trade concepts must first be suitably adapted to the OLG framework in which the model is embedded. Below, an identification of regime preferences across countries, but within a generation, determines whether or not trade is mutually advantageous at that point in time. Similarly, the identification of regime preferences across generations, but within a country, determines whether there are intergenerational winners and losers.
There is, of course, already a sizable literature that reexamines the gains from trade in dynamic environments. Some of the recent work in this direction has made use of the two-sector overlapping generations (OLG) model, as does the model that follows, and is therefore deserving of specific comment. Serra (1991) and Fried (1980), for example, provide welfare analyses of commodity trade for a small country, in environments with and without reproducible capital goods, respectively. Both Galor (1994) and Kemp and Wong (1995) include reproducible capital and examine small countries, and further incorporate the possibility of asset trade. In a small country model, Bental (1985) examines the welfare implications of asset trade, given the existence of free commodity trade. Kareken and Wallace (1977) do likewise in a two-country model, although their asset is nonreproducible capital (land). It is significant to note that in each of these models it is demonstrated that an uncompensated move to openness may harm some or all of the economic agents engaged in trade.
Collectively, however, this research falls short of providing the straightforward, growth-modified version of the static trade model that is pursued here. Most particularly, the small-country assumption—employed by all but one of the above-mentioned articles2
Kareken and Wallace (1977) provide the only exception; their model, however, assumes a nonreproducible physical asset (land), and is therefore not a growth model.
A related literature provides a hint, however, as to what can be expected in the absence of a small country assumption. This literature utilizes the one-sector OLG model to examine the welfare implications of international factor mobility. Buiter (1981) examines financial openness and Galor (1986) examines international migration, both using a two-country model and assuming different national rates of time preference. Both models emphasize the effects of an introduction of factor mobility on welfare via the endogenous effects on capital accumulation. Moreover, both draw the conclusion that openness narrows or eliminates the difference between domestic steady state capital-labor ratios. Most generally, one of the two countries will incur a welfare loss as a result of this change. Thus, for these models, openness does not deliver unambiguous mutual gains for the two countries.
Finally, it should be noted that the dynamic gains from trade have been analyzed earlier in the context of a two-sector infinitely lived representative agent model.3
However, conclusions drawn from this framework are less than straightforward, primarily because of an incompatibility of the framework itself with the heterogeneity assumptions that trade models typically employ. As a case in point, with differing rates of time preference across countries, steady state in a trade regime requires that at least one of the two countries be completely specialized in production [Stiglitz (1970)], in obvious violation to the starting assumptions of factor endowments trade theory. This incompatibility then serves to highlight the significance of the OLG model to the present study. Since the existence of equilibrium in the two-sector OLG model was established [see Galor (1992)], it has been recognized that this framework does not share this difficulty with heterogeneity [Cremers (2001)]. That is, in a two-sector OLG model, both trading countries may remain diversified along a transition path and in a steady state. This compatibility with diversification requirements implies the promise of the OLG model in producing a more straightforward dynamic analogue to the earlier static trade arguments.4The OLG framework has been utilized to examine other related trade issues as well [see Gale (1971, 1974), Eaton (1987), Galor and Polemarchakis (1987), Matsuyama (1988a, 1988b), Fisher (1995), and Mountford (1998)].
The two-sector OLG model introduced here presents a dynamic reinterpretation of the factor endowments environment that is modified primarily to include, and therefore to clarify the role of, capital accumulation in the welfare analysis. In this dynamic adaptation, countries are assumed to differ solely by the determinants of their factor endowments at each date, or equivalently, by the determinants of their capital accumulation paths. These exogenous determinants include an initial endowment of capital and a national discount factor (i.e., rate of time preference).5
This paper thus follows in the long tradition of the trade literature by assuming inherent differences between countries serve as the basis for trade. A country's initial endowments (here, a capital-labor ratio) may reflect the stage of economic development that has been reached at the time during which a trade regime is being considered. A country's discount rate may reflect a cultural attitude toward saving or even a reaction to environmental considerations that are outside the current modeling exercise, such as the presence or absence of a social security system or the additional possibility of investment in human capital (see also footnote 7). There is no presumption, a priori, that two countries are identical in either of these respects at a given point in time.
The log-linear specification serves three purposes. First, as is well known, it implies that the equilibrium is unique. Second, by simplifying the analytics, it is possible to describe welfare effects for all transitional generations, rather than a subset of generations comprised of those living only during the steady state [as in Galor (1986)] and the initial period [as in Buiter (1981)]. Third, it enables the ambiguity raised by opposing static and dynamic welfare effects to be resolved, and in that sense is essential to the demonstration that trade may not be mutually advantageous in a growth setting.
For simplicity, results are presented for two alternative cases: either the two countries differ only with respect to their initial endowments, or, they differ only with respect to their discount rate. It is shown that, in the first case, the effects of trade on accumulation and welfare are limited to the transitional periods. In the second case, the effects are instead shown to extend into the steady state. Thus, one finding from this exercise is that starting assumptions regarding rates of time preference are not at all innocuous when it comes to characterizing the dynamic effects of trade. A second finding is that, in both cases, the effects of trade on capital accumulation are sufficiently large so as to dominate the traditional gains from trade and therefore determine the direction of the welfare change. That is, the dynamic effects of trade may indeed be stronger than the static effects. Furthermore, the trade-induced changes in the domestic capital accumulation paths cannot be uniformly characterized over time so that, for example, some generations in one country may benefit from an increased capital labor ratio, whereas other generations in the same country suffer from a decreased capital-labor ratio. Consequently, a third result is that trade in a dynamic setting does produce intergenerational winners and losers within each country. Most important, however, trade is shown to eventually, if not immediately, narrow the difference in the pair of domestic capital accumulation paths relative to autarky. Because for one country there is decreased capital accumulation, it can be concluded that the dynamic effects of trade are not always welfare enhancing. More particularly, it is shown that it is the high saving country that will have a lower steady state capital-labor ratio and, as a consequence, steady state generations in this country find themselves worse off as a result of the move to free commodity trade.7
This model suggests that the more advanced economy is the one to be harmed by trade in the long run. That is, in this model, all savings are channeled toward the accumulation of physical capital and, hence, the high-saving country would accurately be regarded as the most advanced of the two countries. However, if the model is viewed as one that has abstracted from human capital accumulation as an alternative to physical capital accumulation, then this interpretation might need revision. That is, it is possible that the country that invests most heavily in physical capital goods is also that which has invested the least in human capital. In this circumstance, it would not be incorrect to say that the least advanced country is the one harmed by trade. Such behavior could be rationalized, for example, in a model that allows two countries to be at different stages in the evolution from an industrialized to a knowledge-intensive economy. [See Galor and Moav (2002) for an example of an evolutionary growth model.]
These results are developed as follows. Section 2 describes the economic environment and derives preliminary optimization results regarding consumption and production. Section 3 describes the equilibrium path for an integrated world economy and also for a two-country version of the same world in both an autarkic and a trade regime. In particular, price sequences and capital accumulation paths are described for both countries under the two regimes, and are further differentiated according to whether the countries differ in terms of their endowments or their discount factors. Also, an expression is derived that reveals the pattern of trade in the free trade regime. Section 4 details the impact of a trade regime on capital accumulation, and the welfare of the initial old, transitional, and steady state generations for both countries in each of the two characterizations of the world. Section 5 summarizes and provides an overview of the results. Concluding remarks are presented in Section 6.
ENVIRONMENT
Production
Consider a world economy in which consumption goods and physical capital goods are produced by firms every period using capital and labor services that are acquired in perfectly competitive factor markets. Let ki(t) denote the factor intensity ratio of industry i at date t, and
, 0 < αi < 1, the per worker production function for consumption goods (i=1) and capital goods (i=2). For any positive capital-labor ratio, these technologies yield a production possibilities frontier, which is strictly concave to the origin. It is assumed that α2>α1, or, that capital-goods are more capital-intensive that consumption goods, and that capital depreciates fully each period. Output of good i per capita at date t is given by xi(t)=li(t)fi(ki(t)), where li(t) denotes the fraction of the working population employed in sector i at that date.
Let k(t) and p(t) denote, respectively, the ratio of capital to labor available in world resource markets and the relative price of the capital good, at date t. With perfect capital mobility across sectors, competitive firms collectively maximize the value of output at given market prices at each date. That is, given k(t), p(t)>0, resource allocations across sectors, ki(t) and li(t), i=1, 2, are solutions to the following problem:
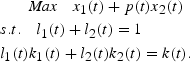
It can be shown that these solutions are given by:
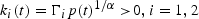
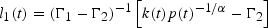
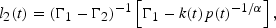
where α=α1−α2<0, and Γi=
i, i′=1, 2 and Γ1−Γ2<0. If the li(t) are positive so that production is diversified, then date t competitive factor payments are given by
and
, where w(t) and r(t) are the date t wage and (gross) rental, respectively, expressed in units of date t consumption goods. Substituting (1) yields,
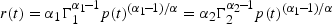
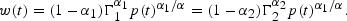
These expressions reflect the well-known Stolper-Samuelson finding; that is, an increase in the relative price of newly produced capital increases the payment to the factor (preexisting capital) used intensively in its production and reduces the payment of the other factor (labor) at the same date.
Finally, full depreciation is assumed so that the world capital-labor ratio evolves according to k(t+1)=x2(t), for all t.
Utility Maximization
Let L denote the constant number of two-period lived individuals born to generation t, t≥1, in the world economy. Let the term “per capita” denote any variable divided by L. Individuals from generations t≥1 are endowed only with one unit of labor when young. The initial old, members of generation 0 alive at t=1, are collectively endowed with the initial capital stock, expressed in per capita terms by k(1), and are each without labor endowment.
For members of generations t≥1, utility is derived from consumption in both youth and old age. When young, individuals use labor income to purchase assets in addition to consumption goods. Old age consumption is financed by the return on these assets. It is assumed that there is only one consumption good and one asset, physical capital. The maximization of lifetime utility subject to the pair of budget constraints imposed during youth and old age for representative agent h, h=1, …, L, of generation t≥1 is given by:
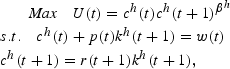
where ch(t) and ch(t+1) denote consumption when young and old, respectively, βh ∈(0, 1) is the individual's discount factor, kh(t+1) is the physical capital demanded when young.
Interior solutions to this maximization problem are the demand functions of the young for consumption goods
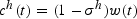
and physical capital
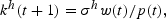
where σh=βh/(1+βh). These demand functions yield an indirect utility function for a member of generation t given by
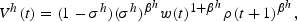
where ρ(t+1)≡r(t+1)/p(t) denotes the return on capital ownership between periods t and t+1. From this expression, it can be seen that the welfare of all generations other than the initial old will depend only on their discount factor and the the wage and the return on capital relevant to their lifetime.
Utility of the initial old is derived entirely from consumption at t=1, purchased with the proceeds from their initial capital endowment. It is assumed that utility of the initial old is increasing in consumption, the latter being given by ch(1)=r(1)kh(1).
AN INTEGRATED WORLD ECONOMY
As a preliminary to the comparison of autarkic and trade regimes, the equilibrium path of an integrated world economy—for which all factors, goods and assets are internationally mobile—is first derived. Let σ=L−1[sum ]σh denote the average savings rate. Then, the world capital market-clearing condition, or, equivalently, the world trade balance condition, is given by
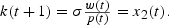
Substituting (5) and the definition of x2(t), it follows that l2(t)=σ(1−α2). Together with (3), it is possible to solve for the equilibrium relative price of capital at date t,
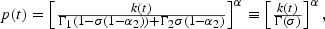
where Γ′(σ)>0. Recalling that α is negative, (8) demonstrates that the date t relative price of capital decreases in the capital-labor ratio at that date and increases with the savings rate.
From (5), (7), and then (8), the equilibrium path for the capital-labor ratio is given by
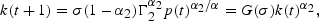
where
and G′(σ)>0. Backwards substitution allows for k(t+1) to be further expressed:
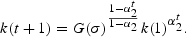
Clearly, k(t+1) increases with both k(1) and σ. However, the significance of the initial endowment decreases, and that of σ increases, over time. Taking the limit of this expression as t→∞, (or substituting k=k(t+1)=k(t) into the preceding equation), gives the steady state capital labor ratio
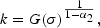
which, as might be expected, is independent of the inital endowment and increasing in σ. (All further variables for which time indices are foregone also represent steady state values.) Note that from (10), for a given σ and k(1)<k, the capital accumulation path increases monotonically and consequently, from (8), the p(t) sequence is decreasing over time. From (5) and (4), respectively, it also follows that the wage will rise and the rental will fall, both monotonically along the equilibrium path.
Now, the t+1 version of (8) and (9) together imply that:
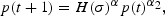
where H(σ)≡
and H′(σ)>0. Substituting p=p(t) =p(t+1) implies that in the steady state,
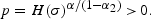
With the relative price of capital falling, or depreciating, over time, it follows from (12) that p(t+1)/p(t) is less than one, increases monotonically along the equilibrium path, and from (13), approaches one as t→∞. Furthermore, because ρ(t+1)=[p(t+1)/p(t)] r(t+1)/p(t+1), the t+1 version of (4) and (12), imply that
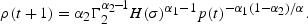
Thus, the effect of the falling rental (diminishing returns) dominates that of a decreasing rate of depreciation, so that overall the return on capital ownership declines monotonically along the equilibrium path.
The evolution of capital-labor ratios and price sequences as just described will determine, via (6), the welfare of each generation in an integrated world economy. In the following section, these derivations also will enable the alternate characterizations of welfare under autarkic and (commodity) trade regimes.
A Two-Country World
It is now assumed that the same world economy is comprised of two countries, indexed by n=A, B, and that the world operates under either a regime of autarky or free commodity trade beginning with t=1. The effects of trade on prices, capital-labor ratios, and utility will therefore involve a datewise comparison of these variables across regimes for each country.8
It might be worthwhile to issue a caution here. It is important to recognize that even in the autarkic regime, both countries accumulate capital endogenously. Thus, in comparing entire sequences of capital-labor ratios under the two regimes, we are questioning whether capital accumulation in a trade regime is greater or less than would be the case in autarky, given identical initial conditions. In other words, the paper does not conduct the much simpler comparison of the capital-labor ratio at successive dates in a trade regime with an unchanging initial value representative of autarky.
It is assumed that the two countries differ only with regard to their initial endowments of capital and their national discount factors. They are therefore identical with regard to the composition and size of their populations at any date, so that each generation born within a particular country has L/2, or one-half of the total, members. The initial world capital-labor ratio is an average of the initial capital-labor ratios of the two countries, k(1)=[kA(1)+kB(1)]/2, where kn(1) denotes the initial capital-labor of country n, n=A, B. Both of these initial capital-labor ratios are assumed to be sufficiently low so that convergence to the steady state in either regime will be from below. Technologies of production remain as described in Section 2 and are everywhere identical. Individuals belonging to generations t≥1 will have preferences as given by (6), although discount factors are now assumed identical within, but not across, countries. Let the discount factor for residents of country n be denoted by βn. The world savings rate is therefore also an average, σ=[σA+σB]/2, where σn=βn/[1+βn], n=A, B. To summarize, the world is comprised of two countries, A and B, which are identical except for the parameters kn(1) and βn (and consequently σn).
With appropriate substitution of this country-specific notation, the equilibrium path of the closed economy described earlier can now be used to characterize either country operating autarkically. That is, for each country, the price sequence is described by (8), (12), and (13) and the capital accumulation path is described by (9)–(11), except that in each equation all savings rates, prices, and capital-labor ratios are now indexed by country. In particular, let kn(t), t>1, be a notation reserved for the capital-labor ratio that evolves in country n in the autarkic regime.
There are a few observations regarding the pair of autarkic equilibrium paths that are useful to acknowledge at the outset. First, in an autarkic regime, capital accumulation paths differ across countries according to their initial endowments of capital and savings rates. If the countries differ only with regard to the former, then the high- (low-) endowment country will have a capital accumulation path that lies above (below) that of both the low- (high-) endowment country and the integrated world economy described in Section 3 at all dates before the steady state, at which time the three paths coincide. Also, the autarkic price sequence for the initially capital scarce country will exceed that of the initially capital abundant country at all transitional dates, but both countries will have identical steady state prices. Second, if countries differ only with regard to their savings rates, then at t=1 they have identical capital-labor ratios, but the country with the high savings rate will ever after have a capital accumulation path that lies above that of the low savings rate country and the integrated world economy. Furthermore, in the initial period and steady state, respectively, the high-saving country will have a greater and lower relative price of capital than the low-saving country. That is, the autarkic price sequences of the two countries will eventually cross.
Turning to the equilibrium path, which evolves under free trade, it should first be noted that this commodity trade regime differs from that of the integrated world economy in that neither factors nor assets are traded. Nevertheless, it is well understood that the equilibrium path of the integrated world remains a valid description of equilibrium prices and world allocations in a commodity trade regime under the proviso that both countries remain diversified at all dates. Moreover, in an OLG model of the type examined here, there also are known sufficient conditions under which this proviso is met, so that diversification at each date need not be assumed exogenously. That is, given sufficient similarity in the initial endowments and savings rates of the two countries, the price sequence given by (8), (12), and (13) generates factor price equalization at every date, while simultaneously clearing world markets at the output levels of the integrated world economy.9
Cremers (2001) provides a detailed construction of these arguments in a more general setting. Here, the relevant diversification conditions are simply stated. If, for n=A, B, i) kn(1)/k(1)∈(Γ1/Γ(σ), Γ2/Γ(σ)) and ii) σn/σ∈(Γ1/Γ(σ), Γ2/Γ(σ)), then both countries A and B are diversified at all dates under the free trade regime.
It remains, then, only to describe capital accumulation paths of individual countries under the trade regime. Let
t>1, denote the capital-labor ratio of country n at date t that evolves in the free trade regime. As only commodities are traded, this capital-labor ratio must satisfy a trade balance condition at each date. With factor price equalization, this condition is given for country n by
for n=A, B, t≥1. Together with world production at the levels of the integrated world economy, this confirms that the world (average) capital-labor ratio at each date under free trade is identical to that of the integrated world, as
σw(t)/p(t)=k(t+1) (see also (7)). Noting further that
(9) implies that, for country n, capital accumulation under free trade is given by
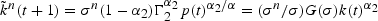
for t≥1. Letting t→∞, the steady state capital-labor ratio in country n under free trade is
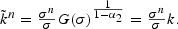
There are again several immediate and relevant implications. First, in the initial period, capital-labor ratios are given and therefore may or may not be equal for the two countries. However, at every subsequent date, the capital-labor ratio of country n in the free trade regime depends on its own savings rate, the world average saving rate, and the world capital-labor ratio of the previous period, but not on the initial endowment or the previous capital-labor ratio of country n. This is because the relative price of capital and the associated real wage at each date in a free trade regime reflect world, rather than country, characteristics. Second, if countries A and B have identical savings rates, it is clear from (14) that they will have identical capital accumulation paths for t>1. With identical endowments and different savings rates, however, the two countries will generate different capital accumulation paths in the trade regime. Thus, under free trade, a country with a higher (lower) than average savings rate will have, as of t>1, a capital accumulation path that lies above (below) that of both the low- (high-) saving country and also the integrated world. Over time, the capital accumulation paths of the two countries will differ only by a factor of proportionality.
The descriptions of the capital-accumulation paths under free trade make it is possible to derive an expression for the net exports of country n. Each country regards
and p(t) as given while maximizing the value of date t output. Substituting these parameters into equations (1) and (3) imply that the date t production of capital by country n in a free trade regime is given by
Demand for capital by country n at that date is given by (14). Substituting (8) and simplifying, date t net exports of capital by country n, denoted by en(t), are given by
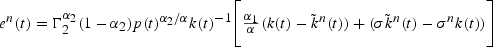
for t≥1. More specifically, for t>1,
and
therefore recalling that α<0,
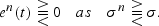
Thus, if there are differences in the savings rates of the two countries, then it is immediate that the high saving country will export capital for t>1 and also the steady state. If there are no differences in savings rates, however, then there is an absence of net trade over both time intervals.
WELFARE
Whether or not individual members of each generation and country experience an increase in welfare as a result of having embarked on a trade regime at t=1 will follow from a comparison of their lifetime utility levels across regimes. To begin the welfare analysis, recall that the effect of trade on the utility of the initial old—members of generation 0—in country n will arise entirely from the effect of trade on the rental earned in that country at t=1. As for transitional generations t≥1 residing in country n, it has previously been noted that utility is determined by the intertemporal preference parameter, now βn, in addition to the date t wage and the date t+1 return on capital (see (6)). In moving from an autarkic to a trade regime, the effect on welfare will therefore be reflected entirely by changes in the latter pair of variables. Suppressing the indexation, the effect of trade on welfare will be determined via
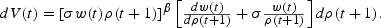
The disposition of each of these generations for or against free trade is revealed by the sign of dV(t). Setting dV(t)=0 defines an iso-utility curve for the autarkic equilbrium in the (ρ(t+1), w(t)) plane with slope equal to −σw(t)/ρ(t+1). The first step in determining the effects of trade on welfare, then, is to compare this slope with a ratio of the trade-induced changes in factor prices, dw(t)/dρ(t+1); that is, with the slope of the date t factor price frontier in (ρ(t+1), w(t)) space. The bracketed expression is positive, equal to zero, or negative as dw(t)/dρ(t+1)>reqless−σw(t)/ρ(t+1). The sign of dρ(t+1), meanwhile, will be shown to depend on the relative characterization of the country.10
The analytics involved in this welfare analysis follow a graphical approach utilized by Matsuyama (1991) to explore the effects of technological progress on transitional and steady state welfare in a one-sector OLG model.
It is instructive, at this juncture, to momentarily digress on the steady state welfare effects to gain some sense of their relationship to more traditional gains from trade arguments. A steady state version of (17) can be expressed by
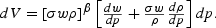
Because ρ=r/p, it follows that dρ/dp=p−1[dr/dp−r/p]. With constant returns to scale, x1+px2=w+rk for each country, so that by the envelope theorem, x2=dw/dp+kdr/dp. Solve this expression for dw/dp and further note that trade balance implies k=σw/p. These relationships then together yield the alternative expression
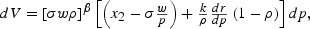
where dp denotes the effect of trade on the steady state relative price of capital. As a point of reference, the first term in brackets equals zero in a closed economy. Solving for dV/dp=0 in the closed economy identifies the return on capital at the golden rule; ρg=1. Thus, with a constant population and full depreciation, the marginal productivity of capital at the golden rule allocation exhibits standard properties. It has been shown [see Cremers (2005)] that the particular savings rate that supports the golden rule capital stock in this environment is given by
As ρ is decreasing in σ, it follows that σ<σg corresponds to ρ>1 and the second term in the bracketed expression is negative. In this case, steady state utility is decreasing in the relative price of capital. Recalling the closed economy of Section 3, an increase in the savings rate will decrease the steady state relative price of capital [see (13)], and thereby raise utility. Moreover, from (11), the increase in the savings rate will simultaneously increase the steady state capital-labor ratio. Taken together, these relationships imply that for σ<σg, steady state utility is increasing in the steady state capital-labor ratio, and thus the steady state is dynamically efficient. Hereafter, it will be assumed that all savings rates considered are below that associated with the golden rule, so that only dynamically efficient steady states are being considered.11
The analysis presented in this paper does carry over to cases involving dynamic inefficiency, although interpretations of the results will differ significantly from those presented later. For brevity, discussion of such cases has been omitted.
As for the commodity trade regime, equation (19) reveals a second factor that contributes to welfare. As
the steady state export of capital goods, the first term in the bracketed expression may generally be either positive or negative. If en>0 (en<0), then increases in p have a positive (negative) effect on the utility of residents in country n living in the steady state; that is, residents of the country that exports (imports) the capital good in the steady state benefit from (are harmed by) an increase (decrease) in their terms of trade. This part of the expression clearly represents the traditional gains from specialization and trade. As this term may either reinforce or couteract the second term in the bracketed expression, their combined effect cannot be signed without further model specification, a task pursued later. The insight critical to the current welfare analysis, however, is that equation (9) leaves open the possibility of a tradeoff between the traditional gains from trade and the effects of trade on capital accumulation, where the welfare effects associated with the latter reflect the positioning of the capital-labor ratio below that of the golden rule.
Returning to the formal analysis, it already has been noted that the switch from an autarkic to a trade regime will change the relative price of capital for each country at each date; this change will further induce respective movements along the factor price frontier, as described by dw(t)/dρ(t+1). From (5) and the t+1 version of (4)
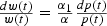
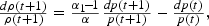
where dp(t) denotes the change in the relative price of capital at date t relative to autarky. The change in p(t) is endogenously determined and, as was noted earlier, reflects a shift from the country-specific savings rates and initial endowments that determine the autarkic equilibrium price sequences to the world savings rate and world initial endowment that generate the equilibrium price sequence in the free trade regime. Denote these changes by dσ and dk(1) so that, for example, dσ>0 for a low saving country that adopts prices generated by the higher world savings rate in the switch to a free trade regime. Similar interpretations may be given regarding the sign of dk(1). Therefore, from (12),
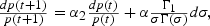
for t≥1. Furthermore, (8) implies that
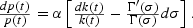
Similarly, the capital-labor ratio of the autarkic and integrated world at each date differ by the same pair of parameter changes (see (10)), so that
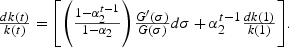
Together these equations give
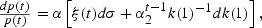
where
In moving to a free trade regime, all prices, capital-labor ratios and savings rates in equations (20)–(25) refer to those of the autarkic regime, although notation to that effect has been suppressed.
LEMMA 1. Suppose dk(1)=0, dσ≠0. There is a transitional date, denoted τ, such that ξ(t)<0 for t<τ, and ξ(t)>0 for t>τ. In the steady state, ξ>0.
Initially,
For
implies that ξ(t) increases monotonically over time. As t→∞,
, which is sufficient to prove the Lemma.
From the Lemma and (25), it becomes evident that the effects of trade on the equilibrium price sequence, and ultimately utility levels, will generally be ambiguous along the transition path. To circumvent this ambiguity, two cases are considered separately (in Sections 4.1 and 4.2, respectively), as the effect of trade on the price sequences, capital accumulation paths and the welfare of each generation within each country are examined: either dσ=0, so that the two countries have identical savings rates at all times, or, dk(1)=0 and they have identical initial capital-labor ratios.
Before proceding with these cases, there are two general and immediate implications of a move to a trading regime that are now simply stated.
PROPOSITION 1. The capital-labor ratio of country n at time t+1, t≥1, under free trade exceeds (is exceeded by, is equal to) that under autarky if dp(t)<0 (dp(t)>0, dp(t)=0). The steady state capital-labor ratio of country n under free trade exceeds (is exceeded by, is equal to) that under autarky as dp<0 (dp>0, dp=0).
The proof is immediate from equations (14), the autarky version of (9), and their steady state equivalents.
PROPOSITION 2. The welfare of the initial old of country n in a free trade regime exceeds (is exceeded by, is identical to) that in an autarkic regime if dp(1)>0 (dp(1)<0, dp(1)=0).
The proposition follows immediately from the t=1 version of (4).
Identical Savings Rates
Suppose that countries A and B differ only in their initial endowments so that kA(1)<k(1)<kB(1) and βA=βB=β. In this case, all differences in the equilibrium paths of the two countries within a particular regime are accounted for by these differences in initial endowments. With equal discount rates, worldwide preferences are homogeneous. Therefore, this environment differs from that of traditional (static) welfare arguments only in that it includes a capital accumulation process in both countries and is embedded in an OLG framework.
For this characterization, the following proposition describes the effects of regime choice on the price sequence within each country. These changes, as noted earlier, represent a move by both countries to a common free trade price sequence.
PROPOSITION 3. Suppose dk(1)≠0, dσ=0. Then dp(t)/dk(1)<0 for all transitional periods and dp/dk(1)=0 in the steady state.
The proof is immediate from (25) and its limit as t→∞.
From Proposition 3, it follows that for capital-scarce country A, for which dk(1)>0 at the opening of trade, the relative price of capital will fall relative to autarky at all dates along the transition path. By Proposition 1, the capital accumulation path of country A under free trade will therefore exceed that under autarky, for transitional dates t>1. Similarly, for initially capital-abundant country B, dk(1)<0, and the relative price of capital is increased at all transitional dates, and the capital accumulation path in these periods is reduced relative to autarky. As noted earlier, in the trade regime, the initial spread in the capital accumulation paths is eliminated in entirety as of t=2, so these describe moves to a common path. For both countries, dp=0, so that by Proposition 1, the steady state capital labor ratio of each country is unchanged by a switch in regimes. With identical savings rates across countries, the steady state capital-labor ratio is also common to both.
To summarize, with dσ=0, the autarkic price sequences of the two countries flank the common free trade price sequence at each transitional date, according to pB(t)<p(t)<pA(t), and converge to a common relative price, pB=p=pA, in the steady state. Also, the autarkic pair of capital accumulation paths lie on either side of the common path implied by free trade during transitional periods, according to kA(t)<k(t)<kB(t), and also converge to a common ratio, kA=k=kB, in the steady state. Notably, the effects of trade on capital accumulation during the transitional periods are asymmetric for the two countries.
It also follows from (16) and dσ=0 that for n=A, B, en(t)=0, for t>1 and en=0 in the steady state. The absence of net trade in the free trade regime arises because the basis for trade is eliminated when capital accumulation paths become identical. At t=1, dσ=0 and (15) are sufficient to imply that country B, with the high initial endowment of capital, will export capital goods to, and import consumption goods from, country A.
Together with Proposition 2, Propositions 4 and 5 will describe the welfare effects of trade on the on the initial, transitional, and steady state generations for the case of identical savings rates.
PROPOSITION 4. Suppose dk(1)≠0, dσ=0. The utility of members of transitional generation t in the free trade regime exceeds (is exceeded by) that of the autarkic regime if dk(1)>0 (dk(1)<0).
Because dσ=0, (25) implies that dp(t)≠0 for each transitional period. Using (20) and (25),
Also, from (21), (22), and (25),
. Together, these relationships imply that dw(t)/dρ(t+1)=−(1−α2)−1w(t)/ρ(t+1)<0. As (1−α2)−1>1>σ, the bracketed expression in (17) is negative. Because, for all t,
it then follows that dV(t)/dk(1)>0 for all dates t comprising the transition path.
From this analysis, it becomes clear that with dσ=0, the factor price frontier is always negatively sloped, and furthermore, always steeper than the iso-utility curve. Trade between the two countries, for which the respective dk(1) are of opposite sign, induces moves in opposing directions along the factor price frontier at every date and accounts for opposing welfare implications. Specifically, for low-endowment country A, the higher world endowment of capital implies that, relative to autarky, wages will rise and the return on capital ownership will fall throughout the transition period. Because this movement along the factor price frontier at each date corresponds to an increase in utility, the transitional generations are unambiguously better off in a free trade regime than in autarky. Conversely, for high-endowment county B, trade lowers the wage and raises the return on ownership relative to autarky at each date, and country B will experience a consequent reduction in utility. Thus, transitional generations in country B are unambiguously better off in the autarkic regime.
PROPOSITION 5. Suppose dk(1)≠0, dσ=0. The welfare of the steady state generations in country n, n=A, B, is unaffected by a switch to the free trade regime.
By Proposition 3, dp=0. As (20) and (21) now imply that there are no movements along the steady state factor price frontier, it follows that dV=0.
Summing up, Propositions 2, 4, and 5, respectively, imply that, for country A, trade worsens the welfare of the initial old, leads to a welfare improvement for the initial young and all transitional generations, and leaves the steady state generations unaffected. For country B, trade improves the welfare of the initial old, worsens welfare for each of the transitional generations and again leaves steady state generations unaffected. Let AU and AU denote preferences for autarky and free trade, respectively, and AU an indifference between the two regimes. Table 1 records these welfare effects in the form of a regime preference for generations born in the indicated time periods in both countries.

From Table 1 it is clear that there is at least one generation in each country that is worse off in the free trade regime. However, in the initially capital scarce country A there is only one generation to suffer from free trade (the initial old), and, thus, by a count of (equally weighted) generations, the opposition to trade in an intergenerational context is rather minimal. In country B, there is instead only one generation (again the initial old) to benefit from trade and thus, the opposition to trade is far more significant in this initially capital abundant country.12
That the initial old may hold regime preferences that differ from those of every other generation within the same country is not a new result [see Fried (1980), for an example in a stationary environment]. The novelty of this finding here is that it demonstrates the same may occur in environments involving capital accumulation.
A second observation is that only in the steady state will concurrent generations in the two countries agree with regard to their regime preferences. The shared view, it is significant to note, is not one favoring a trade regime. And, at every transitional date, only country A, the low-endowment country, favors the trade regime; high-endowment country B has a simultaneous preference for autarky. These opposing regime preferences correspond directly to the effects of trade on domestic capital accumulation, which, as noted earlier, are asymmetric for the two countries during the transitional periods.
Identical Initial Endowments
Now consider the case which initial endowments are equal for the two countries, kA(1)=k(1)=kB(1), but discount rates differ according to βA<β<βB. This case represents a more serious dynamic modification of the static factor endowments model because it allows for differences in the capital accumulation paths of countries in the trade regime and also introduces heterogeneity in the intertemporal preferences of residents of the two countries.13
The end implication of this modification is that the two countries will have different savings rates, a fact that encounters little empirical resistance. There are, of course, other ways of arriving at the same implication but these would unnecessarily complicate the main findings of this paper. For example, Carroll, Overland, and Weil (2000) model habit formation to show that saving rates can be an increasing function of the growth rate.
By assumption, the two countries have identical capital-labor ratios in the initial period. As established in Section 3, both autarky and free trade result in the capital accumulation path of high-saving country B exceeding that of low-saving country A at all subsequent dates. Also established in the same section, the higher than average savings rate implies that autarkic relative price sequence in country B will cross that of the low saving country A from above.
The free trade regime is once again characterized by an identical price sequences in both countries. The following proposition, which describes the effect of trade on the relative price sequence of each country relative to autarky, demonstrates inconsistent effects across time. This highlights the importance of incorporating market-clearing (that is, the large country assumption), in the welfare analysis.
PROPOSITION 6. Suppose dk(1)=0, dσ≠0. Then, dp(t)/dσ>0 for t<τ and dp(t)/dσ<0 for t>τ. In the steady state, dp/dσ<0.
The proof follows immediately from the lemma and (25).
Proposition 6 demonstrates that, with differences in savings rates across countries, the short- and long-run price effects within each country associated with a change from the autarkic to the trade regime will at some point reverse in sign. Thus, for low-saving country A, the relative price of capital will initially rise relative to autarky but eventually fall, whereas-high saving country B will have the opposite experience. In other words, both autarkic price sequences will cross that of the trade equilibrium, country B from above and country A from below.14
It can be shown that τ is increasing in σ, implying that τA<τB. With discrete time, this may or may not be of consequence to the analysis. To avoid this minor and uninteresting complication, it is assumed that both fall between a pair of successive time periods; so that, for example, t< τA< τB<t+1.
The changes in the capital accumulation paths of each country are determined via Propositions 1 and 6. At t=1, the effect of the higher relative price of capital on low saving country A is to decrease the capital-labor ratio of that country vis-à-vis autarky at t=2. The same effect occurs at all transitional dates before τ, with the price above, and the capital labor ratio of the subsequent period below the autarkic value at the same date. After date τ, the now lower than autarky relative price of capital in country A implies a higher than autarky capital-labor ratio in the subsequent period. To sum, the capital accumulation path of country A under free trade will cross its autarkic path from below. The reverse is true for high-saving country B; that is, the capital accumulation path of country B in the free trade regime will cut its autarkic path from above. Therefore, trade implies an initial widening and then eventual narrowing of the gap between capital accumulation paths of the two countries. In both early and late periods, however, the effects on capital accumulation in the two countries are asymmetric. Furthermore, special notice should be taken of the fact that the difference between the steady state capital-labor ratios of the two countries is reduced, but not altogether eliminated, by trade.15
Here, the steady state capital-labor ratio of the high- (low-) saving country in free trade is exceeded by (exceeds) its autarkic ratio. This result contrasts with that of Findlay (1984), for which trade between two countries that differ only in terms of their national savings rate will result in an exacerbation of differences in their autarkic steady states.
As for the pattern of trade, substituting kn(1)=k(1) into (15), implies that in a free trade regime high-saving country B will import capital goods at t=1. From (16), country B will thereafter export capital goods. Both results are reversed for low-saving country A. The steady state pattern of trade is identical to that of the late transitional generations.
Moving on to the welfare analysis, Propositions 2 and 6 are sufficient to give the regime preferences of the initial old. The following proposition will be used to derive the welfare implications for transitional and steady state generations when countries differ only in terms of intertemporal preferences.
PROPOSITION 7. Suppose dk(1)=0,
If dσ<0 (dσ>0), then there is a date
such that free trade increases (decreases) the utility of transitional generations
and decreases (increases) the utility of transitional generations
and also steady state generations.
From dk(1)=0, (20), and (25), it follows that dw(t)=α1w(t)ξ(t)dσ. Recalling the properties of ξ(t), it follows that
for t<τ and
for t>τ. From dk(1)=0,(21), (22), and (25), it also follows that dρ(t+1)=−ρ(t+1)[(1−α1)Γ1/σΓ+α1(1−α2)ξ(t)]dσ, where it can be shown that the bracketed term is initially positive and increasing for all t; therefore,
for all t. The same equations imply that in the steady state,
and
Using these derivations, it is possible to derive the slope of the factor price frontier: dw(t)/dρ(t+1)=−Δ(t)w(t)/ρ(t+1), where
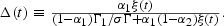
The numerator in this expression is initially negative, increases over time and becomes positive at date τ (see Lemma 1). It can be shown that the denominator is initially positive and increases over time but at a slower rate. Therefore, Δ(t)<0 at t=1, Δ′(t)>0 and, recalling that ξ(t) → Γ1[σ(1−α2)Γ]−1 as t → ∞, Δ(t) → σg as t→∞. That is, the slope of the factor price frontier is initially positive, decreases over time and turns negative for dates t>τ. In the steady state, the slope of the factor price frontier is constant and equal to −σgw/ρ.
From this discussion, it becomes apparent that the second critical term in (17) is positive, equal to zero or negative as Δ(t)[leg ]σ, where σ<σg by assumption. It is immediate, therefore that dV(t)/dσ<0 for t <τ, as Δ(t)<0<σ for these dates. For transitional dates t>τ, then there is a transitional date, denoted
such that 0<Δ(t)<σ<σg for
, but 0<σ<Δ(t)≤σg for
Correspondingly, dV(t)/dσ<0 for
and dV(t)/dσ>0 for
In the steady state, σ<Δ(t)=σg and dV/dσ>0.
To summarize this argument, it is shown that the slope of the iso-utility curve in the (ρ(t+1), w(t)) space is always negative, whereas the slope of the factor price frontier in the same space is initially positive but decreases until also converging to a constant, negative steady state value.16
In a one-sector environment, the slope of the factor price frontier—typically defined by dw(t)/dr(t)—is always negatively sloped. The possibility of a positively sloped factor price frontier in the two-sector environment follows from the definition employed here, dw(t)/dρ(t+1), together with the fact that ρ(t+1)=r(t+1)/p(t)=r(t+1)/p(t+1)[p(t+1)/p(t)] and, thus, changes in ρ(t+1) reflect both the implications of a changing marginal productivity of capital and a changing rate of depreciation.
It can be shown that
is increasing in σ, so that
As before, the complications that may arise are not immediately considered.
A complete characterization of the welfare effects of trade when countries have different discount factors satisfying σA, σB<σg is now presented. As indicated by Propositions 2, 6, and 7, the effects of trade on utility of the initial old, the transitional and the steady state generations are determined entirely by the sign of dσ. In country A, where dσ>0, Proposition 6 implies that dp(1)>0 and thus by Proposition 2, the welfare of the initial old improves in the trade regime. Proposition 7 further indicates that generations
in country A suffer a deterioration in welfare. By the same proposition, both steady state and transitional generations
in country A have improved welfare under free trade. For every generation, the welfare effects are reversed in country B, with dσ<0. Table 2 summarizes these welfare effects in terms of their implied regime preference.
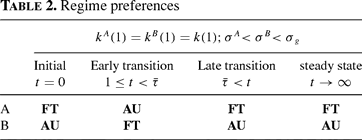
From Table 2, it is again evident that a trade regime will yield intergenerational winners and losers within each country. Table 2 also demonstrates that at every point in time the two countries disagree with regard to the preferred trade regime; thus, the finding of such conflict in the previous section not only is maintained but also is extended to include the steady state generations.18
If the savings rates of the two countries had been allowed arbitrary positions relative to the golden rule, the welfare effects could demonstrate important differences from those described by Table 2. The most interesting possibility involves two national savings rates that straddle the golden rule savings rate. Then, the late generations in both countries would come to an eventual agreement with regard to the choice of regime, both being in favor of free trade. Thus, for these generations it is possible to describe mutual gains from trade.
If the earlier noted distinction between
and
had not been assumed away, there would be only slight modifications of the presented results. With σn<σg, for n=A, B, generations t,
in both countries are now simultaneously in favor of free trade.
The regime preferences of generations born to the steady state can be more clearly understood in reference to (19). In country B, the steady state price of capital rises with trade relative to autarky whereas in country A, the reverse is true. As argued earlier, Country B is a steady state exporter of capital in the trade regime and in that role benefits from the increase in the relative price of capital. Country A is a steady state importer of capital and also benefits from a decrease in the relative price of capital. In other words, the traditionally defined gain from trade, the first term in the bracketed expression of (19), is positive for both countries.
The sign of the second term of the same expression, however, is uniformly negative due to the assumption that both countries have savings rates below that of the golden rule. Thus, the increase in the steady state relative price of capital in country B serves to worsen the welfare of generations born there in the steady state, whereas the decrease in the relative price of capital in country A introduces a positive influence on the welfare of their counterparts abroad. The sign of the second term reflects changes in steady state capital accumulation. Recall that trade always narrows the gap between the steady state capital-labor ratios of the two countries; that is, the steady state capital-labor ratio of high-saving country B falls, and that of low saving country A rises, in the move to a trade regime. With σn<σg, n=A, B, the autarkic steady state capital-labor ratios of the two countries, as well as that of the integrated world, are below those of the golden rule. In the move to a trading regime, the steady state capital labor ratio of low saving country A rises toward (but not above) the golden rule, whereas the steady state capital labor ratio of high-saving country B falls yet further below the golden rule. In country A, the falling relative price of capital is associated with increased capital accumulation, and, consequently, increased domestic production possibilities relative to autarky. Thus, for country A, both the traditional gains from trade and increased capital accumulation contribute positively to utility and free trade is the unambiguously preferred regime. Meanwhile, the rising price of capital in country B is associated with capital decumulation and reflects a loss of production possibilities relative to autarky, thereby introducing a negative influence on utility. With the log-linear specification, the latter effect dominates the traditional gain from trade. Overall, the regime preference of generations born in the steady state is consistent with that which brings the steady state capital labor ratio of the country in which they reside closest to the golden rule.
As for dates before to the steady state, it is also the case that the effects on capital accumulation in the two countries are asymmetric and large enough to dominate the welfare prediction. Recall that, relative to autarky, the gap between the capital-labor ratios of the two countries initially widens but then narrows. In the early periods, during which the gap is widening, capital accumulation is unambiguously welfare improving. Thus, country A suffers a both a decline in capital accumulation and a loss of welfare as a consequence of trade during this time period. In country B, both capital accumulation and welfare are instead enhanced. At date τ, the effect of trade on the relative price of capital in each country changes in sign, and at a lag, so does the effect on domestic capital accumulation and welfare. In the latter periods, capital accumulation is also welfare improving since savings rates are below those of the golden rule.20
That is, both before and after date τ the factor price frontier that is steeper than the iso-utility curve, thus implying that capital accumulation is welfare improving.
DISCUSSION
The dynamic effects of commodity trade are now briefly summarized for the two cases considered, beginning with the effects on capital accumulation. Initial capital-labor ratios are given and do not change across regimes of autarky and trade for either case. When countries have different initial endowments but identical savings rates, the effects of trade on capital accumulation are limited to the transitional periods, where the gap in capital-labor ratios that would have persisted in autarky is eliminated by trade as of t=2. Thus, the country with the greatest initial endowment of capital will see its capital-labor ratio diminished at every transitional date, whereas the country with the least initial endowment of capital will see its capital-labor ratio increased. The two countries have an identical steady state capital-labor ratio that remains unchanged across regimes. When countries have identical endowments of capital but instead differ in terms of their savings rates, the gap between capital-labor ratios that would have appeared in autarky is initially widened, but subsequently narrowed, by trade. Thus, steady state capital-labor ratios for the two countries are more similar under trade than they would have been under autarky, although they do not become identical. The high-saving country will have a lower steady state capital-labor ratio as a consequence of its participation in a trade regime, whereas the capital-labor ratio of the low-saving country will have increased. From these two cases, it can be concluded that commodity trade most often diminishes differences in domestic capital accumulation paths. In that sense, the growth effects of commodity trade are similar to those that would have been produced by financial openness or international migration.21
There is an interesting contrast, however, between this model and those illustrating financial openness. Unlike models of financial openness, the narrowing of differences is incomplete and achieved in a gradual manner. That is, with two sectors and factor price equalization, there is no need for an equality between the pair of domestic capital-labor ratios in either the short or long run. Thus, the instantaneous equality in capital-labor ratios that has been viewed as unrealistic and thus problematic for one-sector models, is irrelevant here.
As for welfare, Tables 1 and 2 make evident that in any given time period the living generations of the two countries are most generally at odds with one another with regard to their regime preferences; that is, conflict between countries is a predominant feature of trade. Although this environment embeds the same possibilities for productive specialization as the static factor endowments model, the static welfare gains may be either augmented, mitigated or nullified by trade-induced changes in the pattern of capital-accumulation for each country. As described earlier, it is never the case that both countries experience increased accumulation as a result of trade. With identical discount rates, long-run capital-labor ratios are unchanged by regime and identical across countries; thus, neither specialization and trade nor altered capital accumulation become sources of welfare change. With differences in discount rates only, the incomplete convergence of capital-labor ratios does imply a basis for long-run gains from specialization in both countries. With discount rates of the two countries uniformly below those supporting the golden rule, trade will bring only one of the two steady states closer to the golden rule and will therefore bring additional benefits to only one of the two countries. Although the country whose steady state moves closer benefits on both counts from trade, the second country does not; the negative welfare effect associated with a capital-labor ratio that lies further from the golden rule dominates the positive gains from specialization. Overall, it can be concluded that even when traditional gains are present, the effects of trade on capital accumulation are of greater significance to long-run welfare, at least for the log-linear specification.
Also revealed by Tables 1 and 2, is the fact that commodity trade in a neoclassical growth model always results in a conflicting view toward trade within each country. Although internal conflict is not new to analyses of commodity trade and welfare, the present case involves conflict between generations rather than the traditional conflict between factors of production. The underlying explanation for intergenerational differences in perspective towards trade is that its effects on capital accumulation are not uniform over time. The initial old, it should be noted, experience only the price effects acknowledged by static trade models. The initial young, experience the same price effect but also an additional, and stronger, capital accumulation effect that is responsible for reversing the regime preference for this and following generations. Thus, conflict between these early generations is ever-present. With different savings rates across countries, and a dynamically efficient steady state, additional conflict may arise within a country as a consequence of a reversal in the direction of change for the domestic capital accumulation path relative to autarky. That is, the regime preference will also reverse from early to late generations.
Finally, it is interesting to note that if this model is placed in a voting context, external conflict in the short run has profound implications for the viability of a trade regime. That is, if the regime on which an economy will embark is determined by a vote at time 0, then voting can be undertaken by the only living generation, namely, the initial old. Without a social planner to consider the welfare of the unborn, the initial old will vote for their preferred regime, even though it may leave every subsequent generation in the same country worse off (see Table 1, for example). More surprising, however, examination of Tables 1 and 2 further reveals that in only one of the two countries will the initial old actually vote for the free trade regime; that is, for both characterizations of the world, there is conflict between members of generation 0. Without international agreement as to the benefits of free trade for the initial old, then both countries will be forced to adopt the autarkic regime in default. Thus, the failure to reproduce mutual gains from trade for generation 0 is, in the absence of a social planner, sufficient to undermine all possibilities for world trade.
CONCLUSION
This paper reconsiders the effects of commodity trade on welfare while incorporating trade-induced changes in the pattern of capital accumulation. In narrowing focus to the most realistic case of the two presented—that where savings rates of the two countries differ—the results can be stated in the simplest and perhaps most startling form. At every date, the effects of trade on the high-saving country are the opposite of the effects of trade on the low-saving country. Relative to autarky, the high-saving country experiences increased capital accumulation during the early periods but decreased accumulation in the late periods, including the steady state.22
Note that the steady state effects described are “level” effects; that is, the steady state growth “rate” is zero in both regimes.
To maintain ease of comparison with the static factor endowments model, this paper has intentionally limited the environment to be one for which there exists a unique steady state equilibrium. It is relatively easy, however, to imagine similar and more pronounced effects arising from an environment that instead allows for multiple steady state equilibria [see Azariadis (1996) and Galor (1996)]. Suppose, in that context, that there are two countries and the low- (high-) saving country converges to its lowest (highest) stable equilibrium in autarky. Then, for the same two countries under trade, it is possible that the world steady state may converge to the lowest of its stable equilibria [see Mountford (1998)]. Despite having a steady state capital-labor ratio that exceeds that of its trade partner (and the world) in the trade equilibrium, it may nevertheless be the case that the high-saving country has a steady state capital labor ratio below its autarkic steady state ratio. In this case, trade has pulled the high-saving country into a “poverty trap” with a dramatic decrease in capital accumulation and a correspondingly large welfare deterioration for its residents.
There are a few perspectives on these results that are worthy of further comment. First, as mentioned in the introduction, an often-made presumption is that the dynamic effects of trade are postive add-ons to the static gains from trade. The results of this paper do not support that presumption, as commodity trade is demonstrated to be detrimental to the growth and welfare of high-saving countries in the long run. Second, theoretically based discussions relating to the effects of trade on growth and welfare outside the neoclassical setting have produced highly ambiguous results. Endogenous growth models that predict a lowering of welfare under openness, however, typically make use of either externalities or monopolistic firms and thus get detrimental effects via the theory of the second best. That is, the removal of one distortion, namely autarky, in the presence of other distortions does not lead to a welfare improvement. In contrast, the negative aspects associated with commodity trade presented in this paper apply even in a first-best, dynamically efficient, world. In this world, the move from autarky to openness involves the removal of a final distortion. Finally, there is currently a great deal of debate regarding the desirability of financial openness for developing or emerging economies in light of the recent and harmful volatility of international capital flows, but there is very little concern associated with trade on the current account. As gradual trade liberalization—in which commodity markets open prior to asset markets—is a reasonable reaction to this debate, it is not at all irrelevant to wonder about the growth and welfare consequences of commodity trade in a world absent international (financial) capital mobility.
The author is grateful for helpful comments received from participants at the Vienna DEGIT VI meetings and the Denver WEA conference.




