INTRODUCTION
It is well known that industrial espionage activities can affect the growth process (Cozzi 2001). In contemporary economies, the most important assets are immaterial: blueprints and production methods are often much more costly1
According to DiMasi, Hansen, and Grabowsky (2003), the research and development of a new marketable drug costs on average around $802 million.
Moreover, in the Congress report held in Buenos Aires on 19 December 2002 we can read: “In addition to information provided by the Intelligence Community, National Counterintelligence Center (NACIC) officers also interviewed a number of industrial security specialists from the selected Fortune 500 companies, representing different sectors of the US economy. All the interviewed companies envisage intellectual information and technologies as the fundamental source of their economic activity and as the first target of misappropriation. As recognized by the interviewed firms, the collection methods for appropriating their knowledge is often legal and include: breaking away from tour groups, attempting access after normal working hours, different personnel appear at the last minute, theft of laptops, customs holding laptops for a period of time, requesting technical information, social gatherings, conferences and symposiums, trade shows, dumpster diving (searching through trash and discarded materials), nonencrypted Internet messages.” Hence, considerable resources are wasted in spying activities.
The immaterial assets are the first objective of appropriation not only by individuals and institutions that have initially developed them, but they also are the object of misappropriation by other individuals and institutions that—at least initially—have not developed these immaterial assets. In particular, ideas that may yield economic benefits to their authors—but on which property rights have not yet been completely established—are the most vulnerable, although of course these are at the heart of the innovative process. Recent legislative innovations in the United States—most notably the Economic Espionage Act (EEA) of 1996—have spurred considerable effort to guarantee the correct functioning of a “weightless economy” mainly based on nonrival assets.
Theoretical analyses of the macroeconomic2
See Grossman (2001) for an interesting microfoundation of intellectual piracy that includes counterespionage activities by firms.
Although Cozzi's (2001) results may be consistent with some well-known empirical evidence of the absence of scale effects generated by a larger R&D effort on the per-capita output growth rate (see, for example, Jones 1995), it predicts that with a growing population the fraction of skilled workers engaged in spying other people's ideas will tend to 1.
Because Cozzi (2001) envisages a fixed number of sectors, it seems interesting to us to test how his results could change considering the fundamental innovative entrepreneurial Schumpeterian activity consisting of a startup with completely new product lines. Following Howitt (1999), we consider a more complex framework in which heterogeneous abilities allow a fraction of population size to undertake research aiming to improve the existing products—either as pure innovators or spies—but also to escape this form of competition in opening completely new sectors. This is also done in light of a recent report suggesting that vertical innovation is the main target of industrial espionage, although this is a new topic for data collection. In fact, from the acts of the Congress held in Buenos Aires on 19 December 2002, we can read: “The majority of the technology targeted in 1999 consisted of components rather than complete systems. This collection trend is associated with both developed and developing countries and seems to be driven by a requirement to upgrade existing platforms, rather than obtain new systems. This means that the existing sectors are the target of intellectual misappropriation and the fundamental aim is to update and upgrade the existing technologies and information in order to maintain the pace of technology accumulation and hence to compete with the existing firms” [italics added]. Hence the vertical innovation process—that is, the upgrading of preexisting products and processes—seems to be the main target of current industrial espionage.
From a theoretical perspective, we maintain that these phenomena may be enhanced by the patent law itself. In fact, a fundamental difference between vertical and horizontal innovation in the R&D–based growth theory is that each horizontal innovation is defined as the introduction of a completely new sector that never existed before, satisfying a yet unsatisfied consumer/producer need, whereas vertical innovation is viewed as the result of an improvement of an existing good or service in a preexisting sector. This distinction between vertical and horizontal innovation is relevant with respect to the main aspects of patent protection. Most notably, Title 35 of the U.S. Code states that in order to obtain a patent grant a product has to be novel, useful, and the improvements with respect to the previous art have to be nonobvious. Sections 102 and 103 of Title 35 of U.S Code define the conditions for patentability, where the novelty requirement of the innovation is defined in negative terms.3
U.S. Code section 102 of Title 35 states that “A person shall be entitled to a patent unless—(a) the invention was known or used by others in this country, or patented or described in a printed publication in this or a foreign country, before the invention thereof by the applicant for patent, or (b) the invention was patented or described in a printed publication in this or a foreign country or in public use or on sale in this country, more than one year prior to the date of the application for patent in the United States, or … (d) the invention was first patented or caused to be patented, or was the subject of an inventor's certificate, by the applicant or his legal representatives or assigns in a foreign country prior to the date of the application for patent in this country on an application for patent or inventor's certificate filed more than twelve months before the filing of the application in the United States … ”
Section 101 of Title 35 of the U.S. Code states that “Whoever invents or discovers any new and useful process, machine, manufacture, or composition of matter, or any new and useful improvement thereof, may obtain a patent therefor, subject to the conditions and requirements of this title.”
Instead, because each vertical innovation builds on previous products, it is far from granted that it will meet the novelty and nonobviousness requisites for obtaining a patent grant. In fact, vertical innovation aims to improving on the previous art, and this process can be ideally decomposed into the summation of continuous and gradual improvements on the existing products. Therefore, such innovation not only has to be novel and useful but also has to convincingly look like a nonobvious improvement on the previous art.5
Section 103 states “(a) A patent may not be obtained though the invention is not identically disclosed or described as set forth in section 102 of this title, if the differences between the subject matter sought to be patented and the prior art are such that the subject matter as a whole would have been obvious at the time the invention was made to a person having ordinary skill in the art to which said subject matter pertains.”
Finally, in the presence of laws such as the EEA, it seems much more dangerous to steal trade secrets regarding a drastically new product line. In fact, it would be much easier to claim that the similar product improvements were being searched for by more firms simultaneously than to convince the FBI that the same completely new product line was being developed almost simultaneously by two independent firms.
Given the macroeconomic focus of this paper, we capture this asymmetric exposure to spying by assuming that only vertical innovation can be spied. This can be interpreted as a drastically reduced form of a more articulated microfoundation of the espionage activity.
The asymmetric exposure to spying of vertical and horizontal innovation allows us to show the existence of a trade-off between long-run productivity growth and income levels related to the enforcement of the intellectual protection of vertical innovations. The work is organized as follows: Section 1 sets up the main framework of our model; Sections 2, 3, and 4 analyze the equilibrium; Section 5 concludes with some comments.
BASIC FRAMEWORK
Let us assume continuous time and unbounded horizon; in this economy there is a mass L(t)>0 of infinitely lived families with identical preferences for nonnegative consumption flows C(t) represented by utility function
, and endowed with a unit mass of flow labor time bearing no disutility; r>0 is the common and constant subjective rate of time preference. Population growth is constant and equal to gL. Capital markets are perfect, the linear instantaneous utility implies constant real interest rate always equal to r. The labor market is perfectly competitive and the inelastic supply of labor L(t) is instantaneously employed by manufacturing firms and by R&D firms. Workers can be hired by intermediate goods firms producing their intermediate goods on a one-to-one basis from labor, or by perfectly competitive R&D firms aiming to improve the quality of an intermediate good and to introduce completely new product lines.
There is a continuum of intermediate good sectors each working under constant returns to scale and free entry. Legally imposed distortions render each of them a local monopoly: this is caused by the Patent System. In fact, in order to stimulate innovation the legislation guarantees that the first to show that she has achieved a nontrivial and useful innovation will be granted full monopoly power over the productive uses of the invention. The legal life of the patent is assumed infinite, but the effective life depends on new discoveries that nontrivially improve on the existing useful invention.
Final output is produced by perfectly competitive firms by combining the fixed factor with a large variety of intermediate goods, according to the following production function:

where Yt is the flow of final consumption good at time t, xit is the amount of intermediate good i produced and used as an input, and Ait is the productivity parameter of the current version of this good. M>0 is the constant aggregate mass of fixed factor (as for example, “minerals, oil”).
Nt∈[0, ∞) denotes the mass of intermediate goods already invented in the economy at date t [ges ] 0. Notice that now t∈R+ is not a product quality index but calendar time. Because in each sector instantaneous Bertrand competition guarantees that only the most advanced patent holder will be producing, Nt also denotes the mass of active intermediate good industries, that is, the mass of producing local monopolies.
In this economy, there exists a different research sector for each intermediate good in which perfectly competing R&D firms try to achieve and appropriate the next generation of that particular good (vertical innovation process). Following Howitt (1999), we consider the leading-edge technological level, with an economy-wide leading edge productivity parameter
that exerts positive R&D spillovers in all sectors. When a new discovery is introduced into an intermediate good sector (a better quality of that intermediate good is introduced) the productivity parameter Ait in that sector jumps to
. This specification incarnates Aghion and Howitt's (1998, Ch. 3) and Howitt's (1999) intersector knowledge spillover: hence the main role of the research firms consists in rendering such spillover endogenous. Therefore, vertical innovation can be considered as the way in which R&D firms try to adapt the most advanced societal knowledge achievements to their own industry.
As in Howitt (1999), the Poisson arrival rate of vertical innovations in any sector is λlt, where λ>0 indicates the productivity in research technology, and where lt is the mass of pure innovator labor time for each intermediate good. As shown in the Appendix (point 1) the economy-wide rate of vertical technological progress is

According to this framework, in equilibrium we will observe an ever-evolving intersectoral distribution of absolute productivity parameters Ait, with values ranging from 0 to
. Defining
, we can concentrate on the relative intersectoral distribution, that—as shown in Aghion and Howitt (1998, Ch. 3) and in Howitt (1999)—converges to the unique stationary distribution of relative productivity parameters—a—characterized by cumulative distribution function H(a)=a1/In γ, with 0[les ]a[les ]1.6
To simplify matters, we suppose that a is distributed according to H([bull ]) right from the beginning date 0.
Following Cozzi (2001), as a result of insecure intellectual appropriability, the author of an innovation could, in each intermediate sector, win the race to the Patent Office with probability
, whereas individual success in spying the newly produced and still unappropriated innovation has density
.
The analysis of the introduction of completely new product lines is borrowed from Howitt's (1999) framework. In fact, we are assuming heterogeneous individual abilities in the horizontal innovation process, whereas there are no quality differences among workers employed in vertical R&D and in manufacturing. Let us define F(θ) to be the distribution of the “entrepreneurial ability” θ, with θ taking value on R+ and with the usual properties F′(θ)>0, F(0)=0, F(∞)=1.
We denote θ0 the “threshold” value of the “entrepreneurial ability”: θ0 ability entrepreneurs are indifferent between trying to develop a new intermediate industry or trying to innovate one of the existing intermediate goods (as a pure innovator or as a spy), to be employed in the manufacturing sector. The individuals endowed by ability greater than θ0 could be engaged in the introduction of a completely new product line.
The horizontal innovation is far less prespecified on the basis of the current state of knowledge and it requires a creativity effort better interpreted in the spirit of Schumpeter's (1934 and 1939) entrepreneurial ingenuity. Moreover, from empirical observations and from the fact that the novelty and nonobvious requirement are immediately met by each horizontal innovation, the creation of a completely new market niche is far less easy to spy than any vertical innovation. In the main part of this paper, we will translate these considerations into the drastic assumption that horizontal innovations cannot be spied at all.
MANUFACTURING, INVENTING, SPYING, OR DIFFERENTIATING?
As proved in the Appendix (point 2), the labor demand function for a sector with relative productivity a at date t is

where
is a labor demand function for the manufacturing firm. Interestingly, the labor force employed in the manufacturing sector depends negatively on the productivity-adjusted real wage. We will focus on the symmetric7
As shown in Cozzi (2005), Howitt's (1999) model also admits a continuum of asymmetric balanced growth paths. It is not difficult to show that all our qualitative results generalize to the case of asymmetric balanced growth paths.

In the LHS of (3) appears the productivity adjusted in the manufacturing sector. The term 0<υR<1 denotes a subsidy to R&D activity financed with a lump-sum tax by the government. Because the government pays the subsidy to all the declared R&D activities, the subsidy is distributed indifferently to pure researchers (vertical and horizontal) and to spies. The RHS of (3) indicates the productivity adjusted expected marginal value product of research
. Vt is the value of a leading edge firm at time t. We have considered the probability of appropriating the new innovation by its true author, the discount rate (r+λlt) and the profit flow accruing to a successful innovator
from date t to infinity.
Each researcher could engage in pure inventive activity by improving the quality of the existing intermediate goods; or she could decide to spy. Finally, the researcher can decide to introduce a new intermediate good. We need an additional arbitrage condition between improving/spying and introducing a new intermediate good. That is [see Howitt (1999)]:

where
. The LHS of (4) indicates the expected flow return improving a product quality, whereas the RHS of (4) indicates the expected flow return from introducing a completely new product line. As in Howitt (1999), each horizontal innovation results in a new intermediate product whose productivity parameter is drawn randomly from the distribution of the existing intermediate products; hence, we can consider the expected value of the long-run cross-sector distribution of the relative productivities. The term ln>0 is a factor of proportionality representing the entrepreneurial labor coefficient in the introduction of a new product line. Hence, θ0 denotes the “threshold” value of the “entrepreneurial ability,” θ, that satisfies equality (4): θ0 ability entrepreneurs are indifferent between trying to develop a new intermediate industry, trying to innovate one of the existing intermediate goods (as a pure innovator or as a spy), or getting employed in the manufacturing sector.
We have to impose the following parameter restriction in order to guarantee the existence of a steady state with positive vertical R&D and espionage activity:

Assumption (A) guarantees that the number of product lines does not outgrow population so as to over dilute consumption demand across sectors and to annihilate any incentive for both vertical innovation and spying. A similar positive lower bound for the population growth rate was implicit in Howitt's (1999, p. 723, Fig. 1) equation for curve (V), where for low population growth rate the incentive to vertical R&D could disappear.
From (4), H(a)=a1/ln γ, and lt=cμ (see point 3 in the Appendix for the derivation of this result) follows

Hence, each individual with an entrepreneurial ability θ>θ0 will find it convenient to start up with a completely new industry line. Hence, in such an economy, for θ>θ0, there will be [1−F(θ0)]Lt individuals sufficiently endowed with “entrepreneurial ability” to pioneer an entirely new industry in which to start up a new intermediate good firm. Instead, all individuals who are endowed with an entrepreneurial ability θ<θ0, that is F(θ0)Lt, will decide either to introduce a better quality of the existing intermediate goods—by inventing or by spying—or to work in the manufacturing sector.
LABOR AND ASSET MARKET EQUILIBRIUM
As shown, each researcher decides to allocate her research labor to inventive activity endogenously, determining a constant amount of per-sector pure inventors. Because each sufficiently endowed research unit—that is, the individuals with ability higher than θ0—can also decide to start up a completely new market niche, the no-arbitrage equation (5) allows us to determine a fixed number of spies in each sector. From (5), we obtain

therefore the number of researchers engaged in the quality upgrade of each of the already existing Nt intermediate goods and the number of spies are fixed in each sector.
Assumption (A) guarantees that in equilibrium the right-hand side of (6) is always strictly positive. Interestingly, from (6) we obtain that the larger the appropriability parameter the larger the number of spies in each sector. This is because the number of purely creative workers is larger, too. Hence, more “preys” (more ideas being created per unit time) stimulates proportionally more “predators” (spies). Moreover, the higher the cost of entrepreneurship the larger the number of spies. This is a consequence of the fact that the only way to get rid of espionage is to try to invent a totally unprecedented product line, that is, to pioneer a new industry.
Notice that now—unlike in Cozzi's (2001) framework—any further increase in the research labor, that is any further increase in population size, will not be only channeled into the espionage activity. More specifically, some of the additional research labor will engage in the horizontal innovation process, which, in turn, will give birth to new industries in which additional manufacturing workers, purely creative vertical R&D workers and spies, will be working.
Let us note that the number of spies is decreasing in θ0. In fact, the number of pure innovators is pinned down in each sector by the inventing or spying arbitrage and θ0 is the “entrepreneurial ability” determined by (5). It follows that the larger the number of spies in each sector the lower the entrepreneurial talent above which people decide to pioneer new industries. Plugging these results into the manufacturing/R&D arbitrage condition (3), and solving the integral yields:

By solving arbitrage condition (7) for
and using (6), we get the labor force employed in the production of each intermediate good

inverting (8) we can determine the productivity adjusted real wage as an increasing function of θ0, i.d. ϖ(θ0). Notice that the existence of R&D subsidies reduces the equilibrium manufacturing employment and production.
As shown in the Appendix (point 4), we can write the labor market-clearing condition as (dropping time index for notational simplicity from now onward)

This equation implies that the larger the number of spies per-sector, the lower the expected profitability of vertical innovation and the more the entrepreneurs encouraged to do horizontal innovation. As we shall see shortly, more entrepreneurs in turn generate faster growth of N.
From equation (9), we obtain a direct and positive relationship between θ0 and the number of sectors/firms per worker

Because the LHS of (10) is a strictly increasing function of θ0, we can invert it and state that in equilibrium there exists a positive relationship between θ0 and (N/L), that is θ0(N/L) with, θ0(0)=0, and
.
This is a natural result. In fact, as the number of sectors grows, more manufacturing and vertical R&D workers (both inventing and spying) are employed, leaving fewer workers in the horizontal innovative activity.
From (1), and classifying sectors by their relative productivities, we can compute aggregate GDP as (see Aghion and Howitt 1998, Ch. 3; Howitt 1999):

GENERAL EQUILIBRIUM
We are now ready to study the balanced growth path of our model and its transitional properties. We will obtain a unique balanced growth path and we will perform a global stability analysis of this steady state. As we shall see, the balanced growth path is globally stable.
From our assumptions about horizontal innovation it follows that:

where
is the cumulated entrepreneurial activity belonging to [θ0(N/L), ∞). We note that this value is a decreasing function of the number of sectors/firms per worker: the greater the number of intermediate goods, the higher the threshold ability parameter θ0, and the fewer the people left to horizontal innovation, thereby reducing the range in which the expected value is obtained.
We can now derive the limit number of varieties produced in the economy, that is, the long run attractor for the number of product lines or horizontally differentiated firms. In fact, define z ≡ (N/L) as the number of sectors/firms per worker. The evolution of z is described by:

which admits a unique and globally stable steady state because of the negative relationship between z and m[θ0(z)], as seen above. Denote the steady state value of z as:

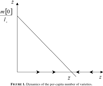
The dynamics can be represented in Figure 1.

Dynamics of the per-capita number of varieties.
Any per-capita number of varieties to the left (right) of
will increase (decrease) over time. Hence, the equilibrium point is globally stable. Moreover, absolute velocity is higher the further z is from the steady state.
The economic intuition for global stability is easily described. Consider a situation with few sectors per-capita. As population increases, in the first place it will be channeled into espionage, exactly as in Cozzi (2001). However, this reduces the returns to vertical innovation and encourages lower ability individuals to try to become Schumpeterian entrepreneurs and to found new industries. This accelerates horizontal innovation by making it proceed at a higher rate than population growth. When the increasing number of sectors has diluted the spy population enough, the profitability of vertical R&D will increase again. As a consequence, entrepreneurship will decline in relative terms, leaving only the more able individuals doing it. In the long run, the number of sectors will tend to increase at the same rate as population growth.
From (10) we have obtained a direct relationship between θ0F(θ0) and z, ∀z∈[0,+∞). In particular, considering the steady state value of z, (13), and defining
, it follows

Notice that the higher the population growth rate, the higher the fraction of population employed in the horizontal R&D sector. Depending on the distribution of entrepreneurial talent in the population, there will exist a lower bound for gL such that the right-hand side of (6) is positive. If population grows too slowly, there will be no steady state equilibrium espionage activity in this economy.
Notice that we can express (13) as

where
is the solution of (14).
Because the LHS of (14) is a strictly increasing and differentiable function of
, the inverse function theorem can be applied and we can write
as a strictly increasing function of λcμ. Therefore, the steady state entrepreneurial ability threshold is an increasing function of the appropriability parameters and of the productivity of vertical R&D. It follows that the steady state per-capita number of sectors is a decreasing function of the appropriability parameters and of the productivity of vertical R&D. Because both sides of (14) increase with λcμ, more appropriability increases the sum of per-sector vertical R&D employment and manufacturing employment. If the interest rate is not too high, more manufacturing in turn implies higher productivity adjusted real wage. The existence of a subsidy to R&D reduces the equilibrium value of the threshold ability parameter
. A larger aid from the public sector to all R&D activities—that is, a larger subsidy υR—reduces the equilibrium value of the threshold ability parameter, and then increases the per-capita number of industry lines.
In the balanced growth path equilibrium a direct and proportional relationship exists between L and N: a greater population size determines a greater number of firms, each producing a horizontally differentiated good. Moreover, as we have seen, the per-capita number of sectors tends to be a decreasing function of cμ, that is, less intellectual appropriability leads to more differentiated product lines. Interestingly, in this way espionage has a positive level effect on per-capita GDP.
Taking into account (8), (13′), and (14), in the balanced growth path we are able to obtain per-capita output and its growth rate as:

The equilibrium level of productivity adjusted per-capita output is a function of all parameters in the model. Profitability considerations in all markets combine in the determination of the long run scale of this stylized economy. Because in this model, following Howitt (1999), only per-sector inventive R&D matters in the determination of the productivity growth rate, the inventing and spying technologies deliver a growth result that appears much less endogenous:

To summarize our main findings, we can state:
PROPOSITION 1. Under assumption (A), the fractions of the population engaged in vertical and horizontal innovation, in vertical espionage, and in manufacturing tend to be positive constants. Along the balanced growth path, per-capita output growth only depends on the growth rate of the leading-edge product quality. The lower the intellectual appropriability, the lower the asymptotic growth rate. Moreover, the lower the intellectual appropriability, the larger the number of sectors per-capita and the higher productivity-adjusted per-capita output. The level of per-capita output does not depend on the population level. Subsidies cannot affect long-run growth rate but positively affect per-capita output and wages.
By a generalization of Cozzi's (2001) model of R&D espionage, we have obtained a trade-off between quality improvement and product differentiation: institutions that guarantee more intellectual protection stimulate more rapid quality improvement, but they reduce product variety and entrepreneurship. Entrepreneurship and research are two aspects of labor creativity that are affected differently by imperfections in intellectual protection. Researchers who target well-specified technical or product improvements are more easily copied than entrepreneurs trying to figure out entirely new industries. Therefore, weaker intellectual protection discourages the first kind of creativity to the advantage of the second. Somewhat paradoxically, espionage encourages entrepreneurship.
The economic mechanism at work is quite natural and easily described. If intellectual property is less protected, vertical innovation will pay off less than horizontal innovation, and a larger pool of people will become Schumpeterian entrepreneurs. This spurs product differentiation and allows a higher level of per-capita GDP. On the other side of the coin, more horizontal R&D has a cost in terms of less vertical R&D, which thereby implies less intense vertical innovation. The economy will tend to stabilize on a long run equilibrium in which constant shares of the population are employed in the manufacturing and undertake the different forms of R&D and spying.
Unlike all existing models without scale effects, in this model population size has no long-run level effect on per-capita consumption. Hence, this model is immune to strong and weak scale effects.8
See Jones (1999) and (2004) for a discussion.
The main growth policy instruments are the effectiveness of espionage law and all the instruments and institutions that might affect the distribution of the entrepreneurial ability of skilled workers. In our framework, a tighter intellectual protection and a higher difficulty to spying increase the per-capita output growth rate and depress the incentive to start up with completely new industry lines. A lower steady state per-capita number of varieties reduce the per-capita output level. This trade-off between per-capita output growth rate and output level can be dampened by all the policy instruments and institutions that shift rightward the distribution of entrepreneurial ability F(θ0). For example, an educational system oriented to develop entrepreneurial capacity, and research institutions (both public and private) that are prone to develop completely new varieties with respect to the already existing and marketed products, could alter the distribution of entrepreneurial ability by shifting it rightward.
The mere existence of imperfect intellectual property rights annihilates the positive growth effects of subsidies to the vertical R&D activity, because in the steady state all additional R&D gets channeled to the spying activity. However, although the per-capita output growth rate remains unaffected by the direct government aid, the R&D subsidy positively affects the per-capita number of varieties existing in the economy, which in turn raise the per-capita output level and the productivity adjusted real wage.
CONCLUSIONS
In this paper, we have shown how accounting for the possibility for R&D firms to escape industrial espionage by searching for entirely new sectors implies that in equilibrium a constant fraction of the researchers will tend to carry out purely inventive activities. Hence, the presence of espionage in the already discovered sectors overwhelms neither horizontal nor vertical creative activities. These questions are motivated by some empirical evidence, which suggests that espionage activity hits the immaterial assets in the existing sectors with the aim of upgrading the products. Since 1995, the annual reports by ORI show that the fundamental aim of espionage activity in both developed and developing countries is to update and upgrade their existing technologies, that is espionage activity seems to hit the existing product leaders.9
We refer the reader to the Introduction for the empirical evidence on this point.
We have drawn the long-run macroeconomic implications of the assumption that the current institutional conditions allow the safer appropriation of an innovation by its “pure” author who invents a completely new product line rather than by who ameliorates existing products. In particular, we obtain that a growing population does not imply a growing fraction of spies to R&D workers, but this fraction will tend to a constant. This result seems corroborated also by indirect evidence. In fact, although industrial espionage is on the rise, available evidence does not suggest that the fraction of spies in the economy is tending to 1, as Cozzi's (2001) model implied.
In this paper, the effectiveness of espionage law in deterring the misappropriation of ideas in the process of being developed is the main policy instrument. We have shown that increasing intellectual protection against spies implies more quality upgrading, but it also will have a negative effect on entrepreneurship and on product differentiation. In fact, a greater ease of spying produces a positive effect on the number of entrepreneurs engaged in horizontal innovation, and, hence, on the flow of new sectors per unit of time. Because the per-capita output growth rate depends on the vertical innovation productivity, whereas per-capita consumption depends positively on the per-capita number of sectors, the less perfect intellectual property rights lower the per-capita output growth rate but raise the productivity-adjusted per-capita output levels.
Moreover, the existence of a direct aid to R&D through a subsidy to all research activities does not affect the per-capita output growth rate of the economy. However, a higher subsidy rate induces a larger mass of individuals to start up with completely new industry lines, thereby increasing the per-capita number of varieties, real wages, and the per-capita output level.
We would like to thank an associate editor and two anonymous referees for very helpful and detailed comments and suggestions. We also thank Vincenzo Denicoló for useful suggestions.
APPENDIX
1. In this first part of the Appendix, we derive the economy-wide rate of vertical innovation described in (2). As in Howitt (1999)
grows deterministically at a rate proportional to the per-sector rate of vertical innovations measured by λlt, with a factor of proportionality equal to ln γ>0, where γ>1 is a constant factor measuring the increase of the productivity parameter
. As the economy develops an increasing number of intermediate goods, an innovation of a given size in any product will have a smaller impact on the aggregate economy; hence, the marginal impact of each innovation on the stock of public knowledge will be ln γ/Nt. The aggregate flow of vertical innovations is the number of intermediate goods Nt times the expected flow of vertical innovations per sector λlt times the marginal impact indicated above by ln γ/Nt. Q.E.D.
2. We here obtain the labor demand function for an intermediate sector. Applying Aghion and Howitt's (1992 and 1998) methods, it is easily seen that the intermediate good i production level that maximizes the monopolist profits at time t is

Because the distribution of relative productivities is unchanging, we do not classify the sectors by their index i, but by their relative productivity
. Defining the productivity adjusted real wage as
and normalizing the fixed factor to one (that is positing M=1), we can rewrite the labor demand function for a sector with relative productivity a at date t as in the text. Q.E.D.
3. Repeating Cozzi's (2001) analysis for every sector, it is easy to see that the inventing or spying arbitrage condition determines the fixed number of research labor engaged in pure inventive activity lt. Each research unit allocates its research labor to the inventive activity by solving

subject to l+s=m, l[ges ]0, and s[ges ]0. Here s and l are, respectively, the time that each research unit spends in spying or inventive activity. The first term of the maximization problem indicates the expected profit flow from the purely inventive activity, whereas the second term indicates the expected profit flow from the espionage activity. Hence, at interior solutions—that is, with positive espionage activity—the arbitrage between inventing and spying gives the constant amount of per-sector pure inventors, lt=cμ. Notice that the R&D subsidy affects the pure research and the spying activity in the same way. Q.E.D.
4. We now derive the labor market clearing condition (9). Because the total mass of existing intermediate goods at any time t is Nt (equal to the total number of firms each producing an intermediate good), the total labor force employed in the intermediate sector is Nt[xcirc ]
. Because Lt denotes the population size at time t, the labor market clearing condition for manufacturing, vertical innovation, and spying is:

where
is the labor demand function per sector with relative productivity parameter a at the date t, and h(a) is the density function of the distribution of relative productivities H(a) seen above. By following the same derivation as in Aghion and Howitt (1998, Ch. 3, App. 2) we obtain equation (9). Q.E.D.