INTRODUCTION
In history, the evolution of global income distribution has been characterized by shifts in the ranking of countries, as well as by divergence or convergence among them. As documented by Maddison (2001, Table B-21), the Netherlands, whose per capita GDP had been the highest in Europe since 1600, was overtaken by the United Kingdom by 1870, and then economic leadership shifted to the United States at the beginning of the twentieth century.1
In Maddison's (1982, Table C.10) productivity ranking among 16 countries between 1870 and 1979, Abramovitz (1986) finds that Australia fell by 8 places, Italy by 2½, Switzerland by 8, and the United Kingdom by 10, whereas the United States rose by 4, Germany by 4½, Norway by 5, Sweden by 7, and France by 8. See Jones (1997) and Pritchett (1997) for empirical discussions on convergence and divergence.
Growth theorists have attempted to construct the theoretical foundations that account for these unpredictable phenomena. Among others, Brezis, Krugman, and Tsiddon (1993) argue that overtaking reflects a leading country's failure to switch to a new technology that is initially less productive than the existing technology. Goodfriend and McDermott (1998) develop a model in which familiarity with a trading partner facilitates knowledge inflows and enhances learning productivity, human capital accumulation, and economic growth. Overtaking results from unilateral familiarization of a less-developed country with the leading country. Galor, Moav, and Vollrath (2005) suggest that although land abundance is beneficial for the process of development in the early stages, land inequality hinders the implementation of educational reforms.2
Among other related theories, Fischer and Serra (1996) demonstrate that a highly equal country tends to overtake an unequal country in the presence of a human capital production function characterized by concavity and externality. Mountford (1998) finds overtaking by a country with a high saving rate in a dynamic version of the standard Heckscher-Ohlin model.
This research examines the role of income inequality within countries in the emergence of overtaking in economic performance among countries. By focusing on two opposing effects of inequality on factor accumulation, it examines the link between income distribution and the pattern of development. The important premises here are that individual savings are convex with respect to income, whereas returns on education are subject to diminishing marginal returns. In these circumstances, inequality promotes the accumulation of aggregate physical capital by stimulating the savings of the rich.3
See Keynes (1936), Kaldor (1978), Stiglitz (1969) and Moav (2002) for theoretical considerations, and Mayer (1966) and Dynan, Skinner and Zeldes (2004) for empirical evidence. The last paper supports bequest motives as in Becker and Tomes (1986), in explaining higher saving rates for higher-income groups.
Galor and Zeira (1993) present a seminal theory in this field. Flug, Spilimbergo, and Wachtenheim (1998) draw evidence from cross-country and panel regressions that credit market imperfections and unequal wealth distribution have negative impacts on average secondary enrollment. Perotti (1996) empirically supports the view that income equality encourages both male and female educational attainment.
The relationship between income distribution and economic growth has been one of the most controversial topics in macroeconomics over the last decade. Despite the considerable number of empirical investigations, little is known about the relationship between these two elements within a single country. Most studies in the 1990s support the view that inequality is a hindrance to growth, whereas some recent articles find that their relationship turns positive in the short run.5
See Barro (2000) as well as Benabou's (1996) careful overview of the empirical studies in the early 1990s. A recent empirical work by Forbes (2000, p. 885) concludes that “the relationship between inequality and growth is far from resolved.”
For instance, Banerjee and Duflo (2003) argue that the differences in previous estimates can be explained by the linearity of the estimated models. Atkinson and Brandolini (2001) find it inappropriate to simply use “high-quality” observations in Deininger and Squire's (1996) data set on income inequality.
The proposed theory attributes the overtaking phenomena to a qualitative change in the combined effect of inequality on factor accumulation. The positive effect on physical capital formation is dominant at low levels of output. This is because, under low output and thus low wage rates, the saving-rate differential between the rich (capitalists) and the poor (workers) is significant, whereas investment in education provides few benefits.7
An empirical study by Perotti (1996) finds that income equality encourages investment in education more significantly in a group of high-income countries.
Note that this reversal is not a sufficient condition for the emergence of overtaking, as high wages ultimately permit educational investment by the poor in developed stages. What is additionally necessary is the diverse degrees of within-country inequality among countries in their initial development stages: On the one hand, high inequality delays human capital accumulation significantly and thereby generates the aforementioned reversal before the wage rate becomes sufficiently high. This early reversal leads the inegalitarian economy to a steady state where the poor cannot afford to invest in education. On the other hand, an egalitarian economy is driven by universal investment in education and converges to a steady state characterized by higher output and persistent equality.8
Due to the convexity of individual savings, a certain amount of initial resources is necessary to ensure subsequent capital accumulation. This paper does not go into the case of zero (or negative) growth resulting from the scarcity of initial resources.
These results indicate that initial income distribution plays a significant role in determining both long-run economic performance and the welfare of individuals.9
This is the notion emphasized by two seminal papers, Banerjee and Newman (1993) and Galor and Zeira (1993).
While this is a meaningful implication, in this article, initial inequality is taken as exogenous and it is not political factors but (endogenously determined) low wages that generate persistent inequality. Galor and Moav (2006, in press) alternatively propose a political economy view that capitalists would be willing to support the accumulation of human capital by workers in order to sustain their profit rates.
In addition to the two types of economies mentioned here, it is shown that an economy with moderate inequality may catch up with an egalitarian economy after being overtaken. Moderate inequality mitigates delays in the spread of education across individuals, and thus wages can reach a level that permits educational investment by the poor. Then credit constraints become less binding among the poor with the reduction in inequality, and the resulting universal investment in education leads the economy to a developed steady state. As a result, the evolution of inequality displays an inverted U-curve, as conjectured by Kuznets (1955).
The theory also reveals that convergence or divergence may occur instead of overtaking, depending on the initial degrees of inequality and the respective development stage of the countries concerned: Countries with similar degrees of inequality converge to similar growth paths, as long as their initial resources are sufficient to ensure the subsequent capital accumulation. Countries with differing degrees of inequality tend to diverge from each other if they are already at an intermediate stage of development. In this sense overtaking is perhaps less probable than divergence in the current world economy, which is more developed than ever.11
The other central reason is that, as argued by Galor and Moav (2004), nowadays international capital markets encourage the flow of capital across borders, making domestic savings less important for physical capital accumulation.
The general tendency toward divergence is supported by some empirical evidence. Benabou (1996) examines the role of inequality in the economic development of South Korea and the Philippines, which were similar with respect to all major macroeconomic variables such as GDP per capita, population, urbanization, and secondary school enrollment in the early 1960s. As a key factor to interpret South Korea's superior economic performance over the next 25 years, he points out significant differences in their initial distributions of income and land ownership: Inequality was much lower in South Korea as a result of its successful land reform following World War II. In fact, the combination of equality and rapid growth also was achieved by other East Asian economies (Hong Kong, Indonesia, Japan, Malaysia, Singapore, Taiwan, Thailand) during 1965–89 (Birdsall, Ross, and Sabot 1995). Engerman and Sokoloff (2002) and Galor, Moav, and Vollrath (2005) propose the relevance of different distributions of land ownership and human capital to the divergence in income levels between North and Latin America in the second half of the twentieth century.
The analytical framework is based on Galor and Moav's (2004) unified growth model that features capital market imperfections, altruistic linkage, capital-skill complementarity, and the above-mentioned contrasting properties of the saving and human capital functions.12
When physical capital is complementary with human capital in production, returns on and the demand for skills rise with capital intensity. See Goldin and Katz (1998) for empirical evidence.
Galor and Weil (2000) and Galor and Moav (2002) theoretically analyze the transition from stagnation to sustained growth in the longer term. Unlike this research, they do not discuss the role of income inequality.
The development path proposed by Galor and Moav (2004) corresponds to the case of moderate inequality explained earlier.
The rest of the paper is organized as follows. Section 2 outlines the basic structure of the model, and Section 3 derives short-run equilibrium. Section 4 finds the multiplicity of steady-state equilibria, and then elucidates the global behavior of the dynamical system that governs the evolution of inequality. Utilizing these results, Section 5 analyzes the impact of income distribution on the behavior of output growth, by comparing the growth paths of hypothetical economies that differ only in their initial income distributions. Section 6 summarizes the discussion and proposes future research. Proofs of technical results are placed in the Appendix.
THE MODEL
Consider a closed overlapping-generations economy operating over an infinite discrete time horizon, starting with period 0. Individuals with perfect foresight invest in assets and education in the presence of imperfect capital markets. In perfectly competitive environments, producers generate a single final good that can be consumed or passed on to the next generation. Population and technology are exogenously determined and stationary over time.
Producers
The amount of aggregate output produced at time t, Yt, is determined by the aggregate stocks of physical and human capital at time t, Kt and Ht, respectively. The production function takes the Cobb-Douglas form:

where α∈(0, 1), kt≡Kt/Ht, and A>0 stands for the level of technology. The market price of the final good is normalized to 1.
In contrast to individuals' loans taken out to cover the cost of education, producers freely rent the services of capital and labor from households through competitive factor markets.15
This assumption is consistent with the fact that compared to human capital, physical capital is easily collateralized.

Note that the rate of return on human capital, wt, increases with physical capital because of the complementarity between the two types of capital. Physical capital depreciates at a constant rate
in each period.
Households
Environment
A new generation of individuals is born in every period, living over the course of two periods. Namely, there are two generations in society at any point in time. Individuals may be different in their initial wealth, yet they are homogeneous in terms of all other aspects. The population size of each generation is normalized to one, and an individual born in period t is referred to as a member
of generation t.
In the first period of life, when young, a member i of generation t engages in skill acquisition. Human capital formation is augmented by physical investment, without which an individual will obtain only basic skills. In this circumstance, the individual allocates transfers from her single parent, bti, between education, eti, and savings, sti. That is to say,
In the second period of life, when an adult, the individual acquires human capital
, where h(·) is an increasing and strictly concave function defined on
satisfying h(0)=1 and the Inada conditions.16
Alternatively, the minimal level of labor h(0) can be viewed as the level of human capital acquired by public primary and secondary education. In this case, inequality still generates differences in individual attainments in higher education.
, is

where Rt+1=1+rt+1−δ≡R(kt+1).
The preferences of a member i of generation t are defined over
, consumption in period t+1, and
, transfers to her single child.17
One may suppose that
includes the consumption of her child.

where β∈(0, 1) and
. The underlying premise here is that intergenerational transfers are a luxury good and are motivated by the “joy of giving.” The budget constraint faced by the individual is

Optimization
Each member of generation t maximizes her utility from (4) subject to (5). The optimal amount of transfers chosen by a member i of generation t is

where
. The convexity of this transfer function asserts that inequality in wealth It+1i across individuals enhances aggregate transfers.
Noting that the resultant indirect utility strictly monotonically increases with It+1i, this member chooses educational expenditures eti so as to maximize It+1i in (3). Hence, the optimal level of education where no credit constraints exist, denoted as et, is
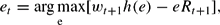
where the factor prices are taken as given and predicted accurately. In light of (3) and the properties of h(·), the education level et is a unique maximum satisfying the first order condition

Without loss of generality, it is assumed that no physical resources are invested in education if the economy is expected to be inactive in the next period; that is, et=0 if kt+1=0. It then follows that there exists a continuous single-valued function

where e(0)=0 and e′(kt+1)>0, implying that et>0 as long as kt+1>0.18
That is to say, this paper omits Galor and Moav (2004)'s Regime I, where et=0 and kt+1>0 (i.e. no investment in education), by assuming that h′(e)→∞ as e→0. As will become apparent, however, this omission does not alter the dominance of the capital-enhancing effect of inequality in the early stages of development.
Note that et is the amount that any member of generation t is willing to invest if she can. In this economy, however, imperfect capital markets completely limit individuals' access to credit and all of them cannot necessarily afford et. Bearing this in mind, the optimal level of education for a member i of generation t, eti, is

Hence, eti may differ across individuals, depending on the transfers they receive. The resultant savings are

It follows from (6) that individual savings sti are convex with respect to wealth Iti.19
This convexity holds within each household, rather than for each individual, in the sense that
is the savings by a member i of generation t, whereas
is the wealth owned by her parent. By contrast, Galor and Moav (2004) assume that adult individuals accumulate savings, so that individuals' savings are convex with respect to their own wealth. Such difference is not essential for the main results later, and to simplify the exposition this paper does not follow their assumption.

This shows that members receiving more transfers will earn more income, as a result of the monotonicity of returns both on physical and on human capital investment.
Group Structure
In period 0, there are two income groups, R (Rich) and P (Poor), which respectively comprise fixed fractions λ∈(0, 1) and 1−λ of adult individuals. The entire stock of initial physical capital is owned by group R, and the initial members of group P have only basic skills as a means of earning income. Because there is no within-group heterogeneity, their descendants can be fully classified by i=P, R in each period.
The government may execute a redistribution policy in period 0. For the sake of simplicity, suppose that redistribution is accomplished by using a lump sum transfer τ among adults, in such a way that
It follows from (6) that initial transfers are

where it is assumed that
for technical convenience.20
This assumption is made so that equation (32) below can be applied to period 0. However, this is not essential for the qualitative results, and one may alternatively assume that members of group R have only basic skills.

In other words, the initial wealth ranking between the two groups never reverses in the future.
SHORT-RUN EQUILIBRIUM
This section considers the determination of economic variables in each period.
The Capital-Labor Ratio
In this closed economy, savings are the only source for physical capital in the next period. Moreover, note that credit constraints are not binding for members of group R in equilibrium (i.e.,
); otherwise no aggregate savings lead to e(kt+1)=e(0), a contradiction to the fact that
. It thus follows from (11) that

where
denotes aggregate transfers, and nt is the fraction of young individuals for whom credit constraints are not binding in period t. By contrast, equation (10) yields the aggregate stock of human capital:

Accordingly, in view of (9), the capital-labor ratio in period t+1 is

Given the properties of h(·) and e(·), this equation implies a continuous single-valued function

where k(0, 0, nt)=0,
kB(·)>0, and kb(·)≤0 for
(with equality if and only if nt=1). Noting that credit constraints are never binding for group R, nt is determined in a way that

Figure 1 illustrates the determination of nt on the
space, where
The Credit Constraint Frontier CC is defined as the set of all pairs
for which
that is to say,
on the frontier.21
These two equalities hold because q(·, 1)=q(·, λ) if and only if
Without loss of generality, one can choose nt=1 if
so that nt denotes the fraction of young members for whom credit constraints are not binding in period t.
and thus kt+1 go to zero, and its slope is positive and less than unity. Observe that
on the region below the frontier and
on the region above the frontier—both cases are consistent with the definition of nt. Noting that the effectiveness of credit constraints depends on between-group inequality, the
space in the diagram can be divided into three regimes:22
Regimes 1–3 in the present paper are the counterparts of Stages I–III (of Regime II) defined by Galor and Moav (2004). Because, unlike the growth path they focus on, the economy considered here does not necessarily go through Stages I–III sequentially, they are renamed Regimes 1–3 in this paper. The counterpart of their Regime I does not exist here, as mentioned in Note 18.

The Credit-Constraint Frontier CC. On the frontier, credit constraints are not binding for members of group P, and they have no savings (i.e., btP=et).
Regime 1.
: Credit constraints are binding for members of group P, and they acquire only basic skills with no savings.
Regime 2.
: Although all members of generation t invest their endowments in education, credit constraints are binding for group P.
Regime 3.
: All members of generation t attain the educational level et, and credit constraints are not binding for any of them.
It is now clear that the equilibrium capital-labor ratio is expressed as a continuous single-valued function

Aggregate Output
In order to simplify the following analysis of the dynamical system, complete capital depreciation, δ=1, is assumed so that aggregate income equals aggregate wealth in each period.23
This restriction would not contaminate any qualitative properties of the dynamical system.

where Y(0, 0, nt)=0 and YB(·)=Rt+1, as (2) and (7) imply that
Thus, as a result of the properties of k(·) in (18), the function Y(·) is increasing and strictly concave in Bt, and the marginal productivity YB(·) diminishes toward zero as Bt goes to infinity. These results reflect the neoclassical properties of the production function with respect to physical capital. Also, Yb(·, λ)>0 for
and Yb(·, 1)=0, because a rise in btP enhances human capital h(etP) and thus output Yt+1 if and only if credit constraints are binding.
THE DYNAMICAL SYSTEM
Equations (2) and (15) assert that the second period's income
in (12) is affected by the transfer of the other group through the wage and the interest rates (yet not through et because
One may thus write

where Ii(0, 0)=0, as no aggregate transfers lead to no aggregate output in the subsequent period. As shown in the Appendix,

where the equalities hold only if
These properties are a result of the fact that capital income is more important than wage income for group R, whereas the opposite is true for group P. In addition, for
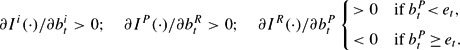
The first two properties above, together with (21), yield that
as
. This Inada condition results from the nonincreasing returns to scale both in physical and in human capital investment, as well as the neoclassical properties of the production function. While the monotonicity of the within-group effects,
is intuitive, the difference in the between-group effects,
is explained by the following three facts. First, as implied by (23), capital income is more important than wage income for group R, while the opposite is true for group P. Second, a rise in
raises the capital-labor ratio and thus the wage rate. Third, if credit constraints are binding, a rise in
will decrease the capital-labor ratio and thus increase the interest rate, otherwise the effect reverses.
Substituting (22) into (6), a trajectory
is fully governed by a two-dimensional first-order autonomous system:

with the initial condition
in (13). It is clear that this system has a trivial steady-state equilibrium (0, 0).
Steady-State Equilibria
This subsection examines the existence of nontrivial steady-state equilibria characterizing the dynamical system (25).
Egalitarian case
First, consider an egalitarian steady-state equilibrium where
∀t. This symmetry implies that all individuals earn the same income and credit constraints are not binding (i.e., Regime 3) in the steady state. It then follows from (18) and (21) that
and kb(·, 1)=Yb(·, 1)=0. In these circumstances the system (25) yields

As a result of the properties of the function Y(·), this condition is satisfied by two positive values of btR if the technological level A is sufficiently high. In order to assure their existence, it is assumed that

where
is the critical level of technology that yields a unique steady-state value
in (26). As shown below, without this condition there is no nontrivial steady-state equilibrium in Regime 3.
LEMMA 1. There is no inequality and
∀t in the steady-state equilibria of Regime 3.
Proof. See the Appendix
This result can be explained in the following manner. Because of the linearity of the return on physical capital investment, given the factor prices, the income It+1i is linear with respect to the transfer
(i.e.,
) for all individuals in Regime 3. In this circumstance, they earn the same amount in any steady-state equilibrium of Regime 3.
Inegalitarian case
Next, consider an inegalitarian steady-state equilibrium where
∀t. This asymmetry and (19) imply that credit constraints are binding for group P in the steady state (i.e.,
. It then follows from (25) that

In light of (17) and (23), decreasing the fraction of capitalists will raise the interest rate and thus their income
, as capital income is more important than wage income for capitalists. This property assures that at least two positive values of
satisfy (27) under (A1). The inegalitarian steady-state equilibrium occurs if
additionally satisfies the condition
a condition that prevents intergenerational transfers within group P.
Let n∈(0, 1] be a steady-state value of the fraction nt. Then (26) and (27) can be jointly expressed as:

Let
and
denote the largest and the second-largest transfers satisfying this steady-state condition. Then it follows that they are expressed as single-valued functions
and
(n) such that, for different fractions of the rich, λS<λL,

where gi≡g(λi) and g*≡g(1) for a function g(·).24
This notation applies to all functions in what follows. In order to obtain (29), note that the function
is continuous on (0, 1], as implied by the proof of Lemma 2 in the Appendix.
Let
a the critical level of transfers such that

implying a single-valued function
. Then, if and only if
there exists an inegalitarian steady-state equilibrium where wt≤θ and
∀t.25
In this case, the pair (
(λ), 0) also generates one of the steady-state equilibria because
LEMMA 2. Under (A1), the difference
is strictly increasing in n.
Proof. See the Appendix.
Thus, the sign of
depends on the level of n if there exists a critical value
such that26
In light of (2) and (30), assumption (A2) is equivalent to assuming that
Because
the left-hand side is smaller than the right-hand side if A is sufficiently large, and the opposite is true if α is sufficiently close to 1. Hence, the equality holds under the appropriate values of α and A.
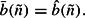
This condition implies that
for a sufficiently small λ, and thus assures the existence of the inegalitarian steady-state equilibrium
characterized by a small fraction of group R. The condition also implies that
; namely, the wage rate is higher than θ in the egalitarian steady-state equilibrium
The analysis below builds on (A2) and refers to λS and λL as significantly different values such that
and
As will become apparent, the economic take-off depends on whether the fraction of group R is either λS or λL.
LEMMA 3. Under (A1)–(A2),
namely{\rm}, long-run aggregate transfers are maximized in the egalitarian steady-state equilibrium
.
Proof. The result follows from (33) and Lemma 4 below, noting that
and
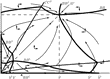
Global Dynamics
This subsection analyzes global behaviors of intergenerational transfers by utilizing a phase diagram. It also reveals the role of initial inequality in determining the long-run wealth distribution. Basic properties of global dynamics are illustrated in Figure 2. In the diagram, there are two income groups, S (Small) and L (Large), which respectively have fractions λS and λL(=1−λS) of population. Either of them becomes group R, depending on the pair
On the region below the 45° line, λ=λS and group S is wealthier than group L. On the region above the 45° line, λ=λL and group L is wealthier than group S. As is apparent from the earlier discussions, the evolution of the economy is independent of λ in the perfectly egalitarian case,
.

The Evolution of Intergenerational Transfers. The regions below and above the 45° line, respectively, depict the evolution of intergenerational transfers for a small fraction of the rich, λS, and for a large fraction of the rich, λL. The pair (btS,btL) converges to one of the points (0,0), ($\skew{-1}\bar{b}^{S},0)$ or $(\skew{-1}\bar{b}^{\ast},\skew{-1}\bar{b}^{\ast}),$ depending on the initial amount and allocation of aggregate transfers.
The space is divided by the two Credit Constraint Frontiers, CCS and CCL, on which
and
respectively. Note that
on the region below (above) CCS, whereas
on the region above (below) CCL. Therefore, Regime 3 occurs on the space surrounded by the two frontiers.
In the phase diagram, the BBi loci, including the interval
on the
axis, are defined as the set of all pairs
for which
.27
The BBi loci reflect the properties of
in (24). They are plotted so as to be gradual, and this way of plotting rules out some steady states that otherwise might exist. As will become apparent, this simplification does not affect the qualitative nature of the dynamical system.
but not at
The pair
converges to one of the points (0, 0),
or
depending on the initial amount and distribution of aggregate transfers.
We are now in a position to examine how the allocation of the initial resources, B0, between the two groups affects the evolution of intergenerational transfers within each group. As will become apparent, initial inequality may play a significant role in determining individual living standards in the long run, depending on the level of
.
First consider the case of B0∈(
by using the diagram.28
The analysis here focuses on the case
, which occurs under assumption (A3) later. As will become apparent, given the initial condition B0∈(
both inegalitarian and egalitarian economies attain positive growth of output per worker in the subsequent periods.
and
, meaning Regime 1 in period 0. Then
grows over time while
remains zero, and the pair
converges to the inegalitarian steady-state equilibrium
in the same regime. As will become apparent in Section 5, the economic intuition here is that the economy encounters a considerable delay in human capital accumulation and thus an economic growth slowdown before
exceeds the take-off level
Because (29) implies that members of group S(=R) obtain the highest long-run income in the inegalitarian steady state, this initial condition is ideal for the rich in the long run as well as in the short run. If, instead of group S, group L holds the entire amount of the initial transfers (i.e., lower inequality), between-group inequality is not persistent. In this situation (29) and Lemma 3 yield that
and
, meaning Regime 1 as in the first case. Because of the relationship
however, there is a period when
is greater than the take-off level
and consequently the pair
converges to the egalitarian steady-state equilibrium
in Regime 3 by way of Regime 2. It should be noted that the economy does not go through Regime 1 if initial inequality is even lower. For instance, in view of Lemma 3, the perfectly egalitarian case
results in
and nt=1 for all t.
Second, consider the case of scarce resources, B0∈(λS
S,
*). As in the first case, high inequality such as
yields
, and thus the economy converges to the nontrivial steady-state equilibria
in Regime 1.29
In the case of lower inequality,
, the long-run result depends on the level of B0: The pair
converges to (0, 0) if
and to
if B0∈(λL
L,
*).
Third, and finally, the allocation of B0 does not affect the long-run outcome if B0<λS
S or
Regardless of initial inequality, intergenerational transfers within each group decrease toward zero in the former case, whereas converging toward
in the latter case.
It is worthwhile mentioning that the diagram illustrates the growth path presented by Galor and Moav (2004). According to their scenario, the initial state is Regime 1 where the number of group R is sufficiently large to assure the take-off condition
However, this does not mean that the population size of group R, λ, cannot be less than 1/2 in their scenario because the critical level of
in Note 6 can be less than 1/2, depending on the structural parameters.
and
. In this case
increases in Regime 1 and ultimately exceeds the take-off level
—a transition to Regime 2. Thus, even though inequality expands initially, the economy converges to the egalitarian steady-state equilibrium where
.
OUTPUT GROWTH
The preceding section showed that the dynamic transition of the economic regime depends on initial inequality. This section considers the underlying evolution of output and thereby examines the impact of income distribution on economic growth.
The Evolution of Output
This section focuses on regime-changing redistribution policies in period 0. Moreover, for the sake of simplicity, the analysis is limited to the development paths on which a chain of intergenerational transfers does not break once it emerges (that is to say,
if
Under these circumstances (12) and (13) yield that

where lt denotes the fraction of adults leaving transfers in period t. The condition lt=λ means that the economy has been in Regime 1 until period t. Hence, the wage rate in Regime 1 is expressed as ω(Yt, λ)≡w(π(Yt, λ)), where π(Yt, lt) is the capital-labor ratio kt satisfying the relationship

Given the properties of the functions h(·) and e(·), one finds that πY(·) > 0, πl(·)<0, π(0, lt)=0 and
It follows from (21) that aggregate transfers are expressed as

Let
be the critical output level below which no individuals leave transfers to the offspring. It follows that B(·)=0 for
BY(·)>0 for
and
The zero-transfer output level
is expressed as a single-valued function
such that
and
In light of (1), (2) and (16), the aggregate income of group R in Regime 1 is Yt−(1−λ)wt=αYt+λw(kt)h(e(kt)). This assures the existence of
and the properties of B(Yt, lt) with respect to Yt. Moreover, the property
follows from the fact that
which is obtained from the relationship

, which reflect the positive effect of inequality on aggregate transfers, are generated by the convexity of the transfer function (6): Because at least θ units of income must be consumed to induce parental transfers, θ is interpreted as the fixed cost of bequeathing. Increasing the ratio of the poor whose income level is below θ saves the total amount of this cost in the economy, and thereby enhances aggregate transfers.
Substituting (33) into (21), the evolution of output throughout the three regimes is given by

where

As shown by Figure 2, the economic regime in period t is fully determined by
and
. The analysis below compares and investigates the evolution of output in each regime.
Regimes 1 and 3
Noting that
in Regime 1 and Φb(·)=0 in Regime 3, the evolution of output in these regimes is expressed as Yt+1=Φ(Yt, 0, lt, nt). Then one finds that Φ(Yt, 0, ·)=0 for
where the zero-transfer output level
is constant in each regime. Moreover, for
,

using (7). The first property above implies that ΦY(Yt, 0, ·)→0 as Yt→∞, noting that BY(·)≤β.
The partial derivative Φl(Yt, 0, ·) above reflects the effect of equality on output through physical capital accumulation. The effect becomes negative and infinitely large as Yt decreases to the zero-transfer output level
where, as mentioned earlier, inequality enhances aggregate transfers. By contrast, the effect turns positive as Yt increases toward
which is defined as a critical output level such that
Since
and
from Note 32, the second result in (35) yields that Φl(Yt, 0, ·)→−∞ as
One also can find that
by noting that ωl(·) in Note 32 has a negative sign.
One can confirm from (17) that an increase in Bt positively affects kt+1, Ht+1, and thus Kt+1.
The property Φn(Yt, 0, ·)>0 shows the positive effect of equality arising from the concavity of the human capital production function h(·). In the presence of credit constraints, equality enhances aggregate human capital by raising the ratio of well skilled workers. Yet this effect is not dominant at immature stages of development; it becomes less significant as Yt decreases toward the zero-transfer output level
This is explained by the fact that these stages are characterized by scarce physical capital, which leads to low wage rates relative to interest rates (i.e., low returns on education relative to savings) because of the capital-labor complementarity in production. That is to say, the scarcity of physical capital, rather than income inequality with credit constraints, is the prime factor for low stocks of aggregate human capital in this situation.
To summarize, although the positive effect of inequality outweighs the negative effect in underdeveloped stages, the relative intensity between these opposing forces reverses in more developed stages where sufficient physical capital boosts wage rates. More formally,

where ε1 and ε2 are sufficiently small positive values.
These results allow the comparison among the levels of output per worker in the egalitarian and the inegalitarian steady-state equilibria. Using (21), they are expressed as

where, as mentioned earlier, g(1)≡g* and g(λi)≡gi for a function g(·). Recalling that
and
note that
is a steady-state output conditional on the economy's presence in Regime 1, whereas
is an unconditional steady-state output in Regime 1. In this sense,
is regarded as a potential steady-state output per worker.
LEMMA 4. Under (A1)–(A2),
S<
L<
* and
.
Proof. The first result follows from (29) and the property Φn(Yt, 0, ·)>0. Regarding the second result, noting that
as well as (21), (30) and (32) yields

which is increasing in lt. It thus follows that
and
. It also follows that the overall effect of equality in (36) is positive for any lt and nt as long as output is greater than
Hence
for any λ and the result follows.
In order to understand the economic intuition behind the properties
and
above, note that the steady-state output in Regime 3,
is higher than the critical level
under the condition (A2). This implies that if λ is sufficiently large, the negative effect of inequality on human capital accumulation is modest and the potential steady-state output in Regime 1,
remains higher than the take-off level
despite the negativity of the overall effect of inequality around
. By contrast, if λ is sufficiently small, high inequality significantly delays human capital accumulation and economic growth as output approaches
and accordingly an unconditional steady-state output
emerges at a level lower than
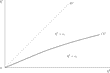
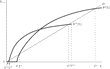
The properties shown above are depicted by Figures 3 and 4. In these diagrams,

where superscripts 1 and 3 respectively are used to denote functions for Regimes 1 and 3. That is to say, Figure 3 illustrates the case in which group R is small in size (i.e., high inequality), corresponding to the lower right part of Figure 2; Figure 4 illustrates the case in which group R is large (i.e., lower inequality), corresponding to the upper left part of Figure 2. The function Φ3(Yt), which is identical between both diagrams, is strictly concave and increasing in
. The function Φ1i(Yt) is also strictly increasing in
although the concavity is not guaranteed. In light of (37), it must be the case that Yt=Φ1i(Yt) for Yt=
,
, and Yt=Φ3(Yt) for Yt=
,
. The diagrams depict the quantitative relationships among the steady-state output levels in Lemma 4. Although Φ3(Yt) is lower than Φ1i(Yt) for low levels of Yt, their relationship reverses somewhere below
.

The Evolution of Output for a Small Fraction of the Rich. There exists a locally stable steady-state equilibrium in both Regimes 1 and 3. In the early stages of development, an inegalitarian economy operates in Regime 1 and produces higher output than a more egalitarian economy in Regime 3. However, the former's output is unable to exceed the take-off level $\skew2\hat{Y}^{S}$, thus converging to the lower steady-state level $\bar{Y}^{S}$ in Regime 1.

The Evolution of Output for a Large Fraction of the Rich. Unlike $\bar{Y}^{S}$ in Figure 3, $\bar{Y%}^{L}$ is a conditional steady-state level of output in Regime 1, because it is higher than the take-off level $\skew2\hat{Y}^{L}$. Hence, even if the economy initially operates in Regime 1, its output ultimately exceeds $\skew2\hat{Y}^{L}$ and converges to the steady-state level $\bar{Y}^{\ast}$ in Regime 3.
Regime 2
The evolution of output in Regime 2 is given by

where
and
It follows that there is no impact of income inequality on aggregate transfers. Hence, for Yt and
in Regime 2, Φn(·)>0 and
, implying that

This result reflects that binding credit constraints cause inefficiencies in resource allocation.
Inequality and the Patterns of Growth
This subsection investigates the impact of income distribution on the output behavior over the entire process of development. The analysis here is limited to the case in which both egalitarian and inegalitarian economies attain output growth over time. For this purpose, (A1) is replaced with a stronger assumption that the technological level A is sufficiently high to satisfy

where Y0 is the initial output per worker.
First consider an inegalitarian policy such that τ=0 in (13). It follows that
and

meaning that the initial state is Regime 1.34
The results in (A4) can be explained in the following manner. Because
as shown earlier, assumption (A3) yields that w0=ω(Y0, λ)<θ for any λ, and thus
. Because, moreover, 0< \b{{}Y}
for any λ, one finds the other results.
remains in Regime 1 in all periods and converges to the inegalitarian steady-state equilibrium
By contrast, if λ is as large as λL, the pair evolves through Regimes 1–3 sequentially and converges to the egalitarian steady-state equilibrium
. Note that aggregate transfers monotonically increase over the first two regimes.
PROPOSITION 1. Under (A2)–(A4),
- The economy characterized by a small fraction of the rich, λS, remains in Regime 1 for all periods. Meanwhile, output per worker increases monotonically and converges to the steady-state level
- The economy characterized by a large fraction of the rich, λL, goes through Regimes 1–3 sequentially. Meanwhile, output per worker increases monotonically and converges to the steady-state level
Proof. The results, except the monotonic growth in Regime 3, follow from (21), (37) and the evolution of transfers described earlier. They also show that the output level is below
during Regime 1, and that Bt>0 and thus Yt>0 in all periods. It thus follows from (38), Lemma 4 and the monotonicity ΦY(·)≥0 that
Y
after Regime 1, implying monotonic output growth in Regime 3.
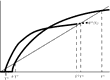
Figure 3 depicts the evolution of output described in Proposition 1(a). Starting out at
Y
, output monotonically increases over Regime 1 toward the steady-state level
which is lower than both the take-off level,
and the steady-state output in Regime 3,
. The economy remains trapped in Regime 1 since wage rates do not exceed the take-off level θ. Figure 4 depicts the evolution of output described in Proposition 1(b). Starting out at
Y
output monotonically increases over Regime 1 toward the take-off level
which is lower than the conditional steady-state output
. In this case Yt eventually exceeds
and the economy enters Regime 2. Because the above proof shows that
Y
afterward,
lies between
* and
, and output monotonically converges to\ the highest steady-state level
Next, consider an egalitarian policy such that a sufficiently large τ in (13) leads to

where
and
), as follows from (26) and (37). It can be seen from Figure 2 that the pair
evolves in either Regimes 2 or 3 in all periods, converging to the egalitarian steady-state equilibrium
in Stage 3.
PROPOSITION 2. Under (A2), (A3), and (A4′), output per worker increases monotonically in either Regimes 2 or 3 for all periods{\rm}, converging to the steady-state level
in Regime 3.
Proof. The results, except the monotonic growth, follow from (37) and the evolution of transfers described above. Because
the properties of Φ3(·) and (38) show that
and that Yt+1>Yt if the economy is in Regime 3 in period t. If the economy is in Regime 2 in period t, it can be seen from Figure 2 that
. This implies that Yt+1>Yt, as Bt=β(Yt−θ) ∀t≥0.
Propositions 1(b) and 2 reveal that moderately or highly egalitarian economies grow toward the steady-state equilibrium where
and
despite the possibility of initially experiencing Regime 1. As asserted later, although the inegalitarian economy in Proposition 1(a) grows faster than these economies in the early stages of development, it ends up with falling behind.
THEOREM 1 (Overtaking) Under (A2)–(A3), consider a group of countries that differ only in their initial income distributions. Although less egalitarian countries may initially attain faster growth of output per worker, they converge to a lower growth path.
Proof. The theorem follows from Propositions 1–2 and Figures 3–4.
The theorem reflects a reversal of the qualitative effects of inequality on factor accumulation in the process of development. As shown earlier, inequality has two opposing effects on factor accumulation: it promotes aggregate savings and thus physical capital accumulation, while constraining the spread of educational investment. Although the capital-enhancing force is initially dominant, it vanishes at high levels of wages (and thus of output), whereas the negative effect of inequality increases with output.35
The adverse effect of credit constraints is reflected in the expanding difference between et and
in the growth process.
is lower than the steady-state output in Regime 3,
Recall that
becomes the unconditional steady-state output if the fraction of the rich is as small as λS. As explained earlier, high inequality significantly delays the accumulation of aggregate human capital and thereby makes the steady-state output level
lower than the take-off level
The point here is that
is not sufficiently high to permit bequeathing by wage earners in Regime 1. In this circumstance, an inegalitarian economy characterized by (A4) and λ=λS converges to the underdeveloped steady state in Regime 1, while being overtaken by egalitarian economies growing to the developed steady state in Regime 3. The failure to take off is likely to occur if the inegalitarian economy is characterized by a large value of α (i.e., disparity in returns between capital and labor), which delays the growth in wages relative to output. In this situation the potential steady-state level
would be lower than the take-off level
, as implied by Note 27. Note that the share of labor income is less important for the long-run performance of egalitarian economies where most individuals obtain asset earnings as well as wages.
By contrast, if the economy is characterized by (A4) and λ=λL, output ultimately exceeds the take-off level
and grows toward the highest steady-state level
in Regime 3. Such moderate inequality mitigates the adverse effect of credit constraints, and thus the conditional steady-sate output
becomes higher than
as depicted by Figure 4. Hence, despite the possibility of being overtaken at some point in time, this economy catches up with more egalitarian economies in the long run.
The developed theory implies that convergence and divergence (without overtaking) are attributable in part to the initial income distributions of the countries concerned: Similarity in this respect leads them to similar growth paths in the long run, whereas dissimilarity propels semi-developed countries to diverge from each other. Such divergence is explained by the fact that in intermediate development stages, sufficiently high wages diminish the saving-rate differential between the rich and the poor, nullifying the capital-enhancing force of inequality.36
Income divergence is not discussed by Galor and Moav (2004), as they deal with only marginal changes in inequality.
Finally, the theory confirms the tendency that individuals have conflicting viewpoints regarding redistribution policies.
PROPOSITION 3. Under (A2)–(A3), egalitarian policies are undesirable from the viewpoint of the rich in any period, even though they maximize long-run output per worker.
Proof. Because the initial condition for positive output growth, (A3), implies that
the proposition follows from the analysis in Section 4 and Theorem 1.
CONCLUDING REMARKS
This research has developed a theory about the role of income inequality in the emergence of overtaking in economic performance among countries. The theory highlights two opposing effects of inequality on factor accumulation. On the one hand, concentrating wealth in the hands of a small group promotes physical capital accumulation, because of the convex behavior of household savings with respect to income. On the other hand, such inequality, together with borrowing constraints, acts as a barrier to widespread investment in human capital—a prerequisite for sustained growth. The former effect works only in early development stages where wages are low, whereas the latter becomes more significant at higher output levels and under wider inequality. The resultant qualitative change in their combined effect permits egalitarian countries to overtake highly inegalitarian countries, which remain underdeveloped.
The essential assumptions for this overtaking phenomenon are the convexity of the saving function, the concavity of the human capital production function, and capital market imperfections. However, they do not assure that overtaking is inevitable. Because the convexity limits the saving-enhancing effect to underdeveloped stages with low wages, income divergence occurs among semideveloped countries if their degrees of initial inequality are diverse. By contrast, countries converge to similar growth paths if they have similar degrees of inequality. These results indicate that the initial levels of inequality as well as of output play a significant role in determining a country's growth pattern.
The established theory asserts that egalitarian policies are undesirable from the viewpoint of the rich, even though they promote long-run economic performance. This confirms the political difficulty of implementing a drastic redistribution in reality, and it is crucial to figure out how to reach a compromise between these conflicting interests. This topic is left for future research.
APPENDIX
Proofx of Equations (23) and (24). Noting that Rt+1=rt+1, the first-order condition (8) is expressed as kt+1h′(et)=α/(1−α) for kt+1>0. In light of this result and (17), the Implicit Function Theorem yields

where
and 0<nt≤1 (and thus kt+1>0). It follows that, in each regime,

Now, (7) and (22) yield that for a given k>0,
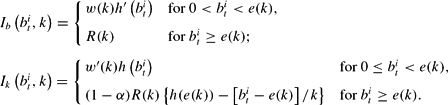
This, together with (17) and (19), yields (23) and (24).
LEMMA 5. If
and k=k(nbi, 0, n)>0, then
for
Proof. Equations (25) and (39) imply that
for
and k>0. Thus if βR(k)=1, the steady-state condition
does not yield the unique value of bi, a contradiction to the one-to-one relationship between bi and k=k(nbi, 0, n). Hence, βR(k)≠1 and the result follows.
Proof. of Lemma 1. Noting the independence of the function
from i, Regime 3 has an egalitarian steady state where
and k=k(bR, 0, 1)≥0. Then in light of Lemma 5 and the fact that
, this k assures that both bR and bP are unique. Hence, the result follows.
Proof of Lemma 2. In light of (28), let
and note the following facts: First, as follows from (23) and Lemma 5,
and
for all n. Second,
, as
is the locally stable steady-state transfer satisfying (26). Third, the steady-state capital-labor ratio
is increasing in both
and n. Therefore, applying the Implicit Function Theorem to (28) establishes that χ′(n)>0 for all n. Because, by contrast,
in (30) is constant for all n, the result follows.
This is a revised version of Chapter 2 of my Ph.D. dissertation submitted to Brown University in 2004. I am grateful to Oded Galor, whose insightful comments and suggestions improved the paper considerably. Furthermore, I wish to thank Gareth Lee, Fumiko Tamura, Kenichi Ueda, two anonymous referees, and participants at Brown University Macro Lunch for their helpful comments.