INTRODUCTION
It is well known that self-fulfilling expectations may cause business fluctuations if there are certain types of coordination failures in the markets. In the real business cycle (RBC) literature, researchers emphasize the importance of increasing returns in generating such fluctuations [Farmer and Guo (1994)]. Increasing returns are usually originated from externalities or monopolistic competitions. Coordination failures also have important implications for economic agents who do not possess rational expectations and try to learn about the economic structure adaptively. The rational expectations equilibrium (REE) may not be “expectationally stable” (E-stable) under learning [Duffy and Xiao (2007); Evans and McGough (2005)]. The recent literature of monetary policy design, however, emphasizes the role of interest rate policies in either facilitating or restraining fluctuations caused by self-fulfilling expectations or E-instability. It is believed that if an interest rate policy is properly designed, it leads the economy to a determinate (free from self-fulfilling fluctuations) and E-stable REE [Bullard and Mitra (2002)]. Determinacy and E-stability have undoubtedly become two crucial criteria in evaluating monetary policies [Evans and Honkapohja (2003)].
Interestingly, when selecting the proper interest rate rules to prevent excess volatilities, researchers prefer to condition on an economic environment that is free from such coordination failures. In other words, the possibility that indeterminacy and E-instability come from a source other than inappropriate policies has been largely neglected. For example, there are extensive studies of the potential benefits and risks associated with Taylor-type interest rate rules. Yet when specifying the economic environment for these studies, researchers seem to ignore the possibility of increasing returns, which are known to cause indeterminacy and E-instability. The workhorse for this area—the New Keynesian model, has monopolistic competitions, staggered prices, but constant returns to scale. Because increasing returns are widely believed to occur in monopolistically competitive economies, one naturally wonders how robust the current findings are if the assumption of constant returns to scale does not hold. Indeed, to some researchers, one is “required” to postulate increasing returns in a monopolistic competition framework, as it is the “only way to account for the absence of significant pure profits in the United States economy” [Rotemberg and Woodford (1995)]. Therefore, incorporating increasing returns into the study of interest rate policy design seems the next logical step to take in extending this research.
In this paper, we propose a first step toward such an extension. We introduce increasing returns to scale into an otherwise standard New Keynesian model with capital, and study the determinacy and E-stability of equilibrium under Taylor-type interest rate rules, as in Bullard and Mitra (2002). Bullard and Mitra's important finding is that if the interest rate rule follows the so-called Taylor principle, the REE of the model is mostly likely both determinate and E-stable. The Taylor principle asserts that the monetary authority must adjust the short-term interest rate more than one-for-one with changes in inflation. Our research question is: when there are increasing returns in the economy, how must the interest rate rules be changed to achieve a stable macroeconomic equilibrium? Does the Taylor principle still guarantee the determinacy and E-stability of the REE?
Our major findings are as follows. We reexamine the determinacy and E-stability of REE under four variants of the Taylor rule studied by Bullard and Mitra (2002). The four variants are (1) the contemporaneous data rule, (2) the lagged data rule, (3) the forward expectations rule, and (4) the contemporaneous expectations rule. Bullard and Mitra (2002) find that in most cases the Taylor principle is sufficient to guarantee both determinacy and E-stability. Moreover, with rule 1 and rule 4 a determinate REE is always E-stable and vice versa. We find that with small increasing returns that are consistent with empirical estimates, these findings no longer hold. In particular, the Taylor principle cannot guarantee either determinacy or E-stability with any of the four rules. In some cases, a less than one-for-one response of the interest rate to inflation can lead to determinacy and E-stability. The policy implications are clear. To rule out indeterminacy and E-instability, it is critical for the monetary authority to identify the level of increasing returns—given a certain level of increasing returns, a distinct set of parameters for the interest rate rule will maintain the determinacy and E-stability of the REE.
The assumption of increasing returns to scale is widely considered in the business cycle and growth literature.1
See, among others, Hornstein (1993), Benhabib and Farmer (1994), Roternberg and Woodford (1995), and Benhabib and Wen (2004).
In general, this paper adds to a series of other research that study the limitations of the Taylor principle as a criterion to design interest rate rules. Benhabib et al. (2001), for example, find that the Taylor principle does not necessarily lead to determinate REEs when there is zero bound on nominal rates. Fair (2005) argues that the Taylor principle cannot guarantee determinacy if aggregate demand responds to nominal interest rates and inflation has a negative effect on consumption. Gali et al. (2004) find that the existence of rule-of-thumb consumers will render the REE indeterminate when the Taylor principle holds. Carlstrom and Fuerst (2005), Sveen and Weinke (2005) and Benhabib and Eusepi (2005) find that in models with capital, the Taylor principle may not yield determinate REE if the interest rate rule does not react to output changes. All these works focus on the determinacy of the REE. We have not seen any papers that challenge the role of the Taylor principle in maintaining the E-stability of the REE.
In the literature, the baseline New Keynesian model ignores endogenous variations in capital, on the ground that capital fluctuations do not correlate much with output at the business cycle frequency [McCallum and Nelson (1999)]. However, a number of researchers have recently pointed out that certain topics can only be studied when capital is allowed to vary endogenously.2
Gali et al. (2004) show that endogenous capital is required for rule-of-thumb consumers to make a difference in system dynamics. Christiano et al. (2001) use investment adjustment costs to generate hump-shaped response of output to a monetary shock. Edge (2000) shows that investment adjustment with a time-to-build technology helps generating a liquidity effect.
The rest of the paper is organized as follows. Section 2 lays out the micro-founded model framework and derives the equilibrium conditions. Section 3 discusses the methodology and calibration of the model. Section 4 presents the results. Section 5 concludes.
A NEW KEYNESIAN MODEL WITH CAPITAL AND INCREASING RETURNS
This is a New Keynesian model with capital. Incorporating capital into a sticky price model is a relatively new topic, and economists have not reached any consensus on how capital should be introduced into the model, and to what extent it will change the determinacy and E-stability properties of the equilibrium. Therefore, before we formally lay out the model environment, we discuss this issue.
Modeling Capital
The standard neoclassical assumption for modeling capital is that households own the capital stock and rent it to firms in a capital rental market in each period. A number of authors [Carlstrom and Fuerst (2005); Dupor (2001); Gali et al. (2004)] have adopted this approach when introducing capital into the New Keynesian Model. This approach is appealing in its simplicity and its consistency with the real business cycle literature. Another approach of modeling capital is to assume that firms own their capital and can only change it by varying the rate of investment. This approach is first advocated by Woodford (2003 and 2004), and is adopted by authors such as Altig et al. (2005) and Eichenbaum and Fisher (2004). This approach is potentially advantageous because it captures the degree of price stickiness in the data without requiring firms to adjust prices too infrequently in the model.
The key question is to what extent adding capital will change the determinacy and E-stability properties of the REE in the model. According to Carlstrom and Fuerst (2005), allowing a rental market for capital in the model will not significantly change the determinacy property of the REE if the central bank follows the Taylor principle in reacting to changes in current inflation. But if its reacts to expected inflation, the equilibrium is much more likely to become indeterminate than in the labor-only model. Kurozumi and Van Zandweghe (2005) study a version of Carlstrom and Fuerst's model, and point out that if the central bank also includes output or consumption in its reaction function, the result will be overturned. Specifically, the expectation based rule no longer facilitates indeterminacy. They also find that with capital, the determinate equilibrium is very likely to be E-stable under adaptive learning. Benhabib and Eusepi (2005) investigate this issue from a global perspective, and conclude that adding capital will generate local and global indeterminacy, unless the interest rate rules also include output as a target. Sveen and Weinke (2005) study the determinacy of REE with firm-specific capital, and find that the Taylor principle does not guarantee determinacy if the central bank only targets inflation. If output is also in the interest rate rules, however, indeterminacy is easily ruled out. We are not aware of any authors who examine the E-stability conditions for models with firm-specific capital.3
Woodford (2004) shows that when capital is firm-specific, the new Phillips curve can be derived using the method of undetermined coefficients, which implicitly requires agents to have rational expectations. Therefore, researchers who study adaptive learning might have to derive the new Phillips curve with the learning assumption first before studying its E-stability conditions.
In this paper, we do not intend to expand on the issue of how capital should be modelled since the novelty of this paper is not capital itself. Our goal is to study the impact of increasing returns, and we need to keep the other parts of the model as standard as possible. Therefore, we choose to adopt the more conventional rental market assumption when modeling capital, and leave the alternative approach for future research. We find that adding capital to an otherwise standard new Keynesian model with constant returns to scale basically does not change the determinacy and E-stability conditions of the REE. In particular, adding capital alone does not change the importance of the Taylor principle in generating determinate and E-stable REEs. This convenient feature will help us isolate the effect of increasing returns. Note that the policy rules we use allow for the interest rate to respond to output changes. Our result is therefore consistent with those of Benhabib and Eusepi (2005), Kurozumi and Van Zandweghe (2005), and Sveen and Weinke (2005).
Households
The economy is composed of a large number of infinitely lived consumers. Each of them consumes a final good Ct, and supplies labor Nt. Savings can be held in the form of real money balances Mt/Pt, bonds Bt, and capital Kt. Consumers seek to maximize lifetime utility

where σ, γ, b, v, χ>0 and 0<β<1. The random shock ut represents shifts in tastes that affect the marginal utility of leisure. This is suggested by Clarida et al. (2001) as a means to incorporate a “cost-push” shock in the inflation adjustment equation. The budget constraint is

and the capital accumulation equation is
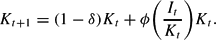
Hence, the consumers receive real labor income (Wt/Pt)Nt, and real capital rental income (Rt/Pt)Kt. Bt−1 is the quantity of riskless one-period bonds carried over from period t−1 which pay out interests at a nominal rate of 1+it−1. Dt are dividends from ownership of firms. Mt−1/Pt are real money holdings carried over from period t−1. The consumers spend their income on consumption Ct, new money holdings Mt/Pt, new bond purchases Bt/Pt, and new investment It. Capital adjustment costs are introduced through the term ϕ(It/Kt)Kt, which determines the change in capital stock induced by investment spending It. We assume ϕ′>0, and ϕ′ ′≤0, with ϕ′(δ) = 1 and ϕ(δ) = δ as in Gali et al. (2004).
The first-order conditions for the consumer's problem can be written as

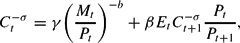
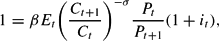
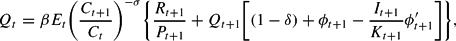
where ϕt+1=ϕ(It+1/Kt+1) and
, respectively. Qt is the real shadow value of capital, that is, Tobin's Q. This is defined as
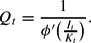
Given our assumption about ϕ, the elasticity of the investment-capital ratio with respect to Q is −1/ϕ′ ′(δ)δ=η.
Firms
There exists a continuum of monopolistically competitive firms producing differentiated intermediate goods. The latter are used as inputs by perfectly competitive firms producing a single final good.
Final goods producers
The final goods are produced by a representative, perfectly competitive firm with a constant returns to scale technology
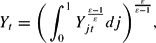
where yjt is the quantity of intermediate goods j used as an input, and ε > 1 governs the price elasticity of individual goods. Profit maximization yields the demand schedule
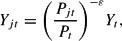
which, when plugged back into (8), yields

Intermediate goods producers
The intermediate goods market features a large number of monopolistic competitive firms. The production function of a typical intermediate goods firm is

where Kjt and Njt represent the capital and labor services hired by firm j, and At is a technology shock. The parameter θ measures the level of returns to scale. When θ = 1, the production technology reduces to the constant-return Cobb-Douglas production function. When θ > 1, the intermediate goods firm has increasing returns to scale.
The firms' real marginal costs φjt is derived by minimizing costs:
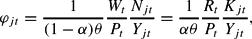
which in turn implies the optimality condition
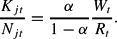
Note that when there are constant returns to scale, (12) and (13) imply that the real marginal costs
are given by

which is equalized across all firms because there is no j in the expression. When there are increasing or decreasing returns to scale, a firm's real marginal costs are associated with its production levels. In this case we can define the average level of marginal costs as

Using (12), (13), and the demand schedule, we can relate the real marginal costs of a firm φjt to the average level of marginal costs φt as
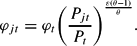
Intermediate firms set nominal prices in a staggered fashion, according to the stochastic time dependent rule proposed by Calvo (1983). Each firm resets its price with probability 1−ω each period, independent of the time elapsed since the last price adjustment. A firm resetting its price in period t seeks to maximize
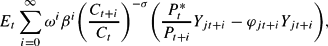
where
represents the (common) optimal price chosen by firms resetting prices at time t.
Finally, the equation describing the dynamics for the aggregate price level is
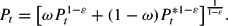
Monetary Authority
The central bank sets the nominal interest rate it every period according to a simple linear rule contingent on information about output and inflation. Following Bullard and Mitra (2002), we consider four variants of the interest rate rule. The first variant is called the “contemporaneous data rule”:
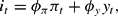
where ϕπ≥0 and ϕy≥0, and it, πt and yt denote percentage deviations of the interest rate, the inflation rate, and output from their steady state values. This is the original Taylor rule that conditions the interest rate on current output and inflation rate.4
In the standard New Keynesian model without capital, the interest rate rule conditions on output “gaps” rather than on output levels. It should be noted that the properties of the REE will not change whatsoever if output gaps are replaced by output levels in those models. See our discussion in Section 2.5.

The third rule is called “forward expectations rule”:
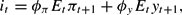
where central bankers use the market's expectations about the future to set the interest rate. The fourth rule is called the “contemporaneous expectations rule”:
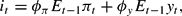
where the underlined assumption is that the market does not have current data and attempts to use past data to estimate today's output and inflation.
Equilibrium and Reduced Linear Systems
The following conditions clear the factors and goods markets:
,
,
and Ct+It = Yt.
We need to derive the linearized versions of the key optimality conditions in order to conduct our analysis. We use lowercase letters to denote percentage deviations of a variable from its steady state value. There are six nondynamic equations and four dynamic equations. The first equation is the linearized version of the labor supply schedule (3):
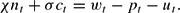
The second equation is the linearized version of (7), which defines Tobin's Q:
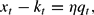
where, to avoid confusion with the nominal interest rate, we have denoted investment by the letter xt. The third and fourth equations are the linearized versions of (12). We are interested in the average level of marginal costs, which are given by

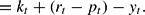
The fifth equation is the linearized production function
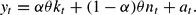
The sixth equation is the market clearing condition
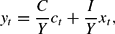
where C, I, and Y are steady state levels of consumption, investment and output.
The first dynamic equation is the Phillips curve, which is derived by solving the firm's dynamic price-setting problem and combining it with (18). The equation is given by

where κ =(1−ω)(1−βω)/ω and B = ε(1−θ)/θ.
The second dynamic equation is the linearized version of (6), which describes the evolution of Tobin's Q:
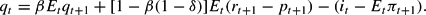
The third dynamic equation is the Euler equation (5), which can be linearized as

The last dynamic equation is the capital accumulation equation (2), which is linearized as
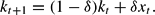
Finally, we add the interest rate rule and use the nondynamic equations to substitute out seven variables qt, wt−pt, rt−pt, xt, it, φt, and yt. The system becomes a four-dimensional linear difference equation system consisting of st =(ct, nt, kt, πt)′ and a vector of shocks εt =(ut, at)′.
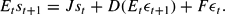
We note that when researchers study the labor-only model, a convention is to convert all variables into “gaps”—the difference between a lower-case variable and its flexible-price counterpart. When capital is added, it becomes very difficult, if not impossible, to make such conversions. Therefore researchers in this field choose to keep the levels of the variables in the system. It is important, however, that when we compare this model with the labor-only model, the gap portion of the variables do not alter any of the fundamental results. To ensure that this is the case, we first convert all the variables in the labor-only model into levels, and then examine the model's equilibrium properties. We find that the determinacy and the E-stability conditions of the labor-only model are not altered at all by such conversion. This ensures us that the comparisons we made in Section 4 are inherently consistent.
METHODOLOGY AND CALIBRATION
General Methodology
Next, we examine the determinacy and E-stability of the REEs with four variants of the Taylor-type interest rate rules. When we study the E-stability properties, we only focus on REEs that are determinate, as in Bullard and Mitra (2002).5
For an analysis of the E-stability properties of indeterminate rational expectations equilibria, see Honkapohja and Mitra (2004) and Evans and McGough (2005).
For each variant of the Taylor rule, the determinacy of the REE is decided by computing the eigenvalues of the system (33). Because there is only one predetermined variable kt, an REE is determinate if the number of explosive roots is three and the number of stable roots is one. If the number of stable roots are bigger than one, we have an indeterminate REE. If there is no stable root, the system is explosive.6
With the lagged data rule, the interest rate rule itself is a dynamic equation with state variables πt−1 and yt−1. In that case, we require two stable roots to yield determinacy.
To study adaptive learning, we rewrite the system as
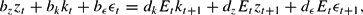
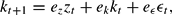
where the second equation is derived from the capital accumulation equation that does not involve any expectations and does not need to be learned. We assume agents have the perceived law of motion (PLM)
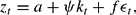
which is in the same form as the MSV solution under REE. The parameter vectors a, ψ and f will have to be learned. Because the properties of the shock vector εt is not essential to our result, we make a convenient assumption that the shock is white noise with mean 0. Given this PLM, we calculate the forward expectation of zt as

Plugging this expression into (34), we obtain the T-mapping from (a, ψ, f)′ to combinations of the true parameters of the model. The model is E-stable if
have eigenvalues less than 0.
It is worth pointing out that the assumptions about agents' information set are crucial in determining the E-stability result. In the baseline case outlined earlier, we implicitly assume that both the private sectors and the central bank observe current values of the variable kt and the shock εt. They use this information to obtain forecasts Etzt+1 and Etkt+1, which in turn determine the current values of zt. This applies to the cases with the current data rule and the forward expectation rule. However, this is sometimes criticized as being unrealistic, since current data are usually not available to economic agents in real life.7
The case with the current data rule is especially controversial. As pointed out by Bullard and Mitra (2002), the central bank has “superior information,” in that it reacts to current values of yt and πt while the private sectors do not possess such information.
Benchmark Calibration
The system (33) has four dynamic equations and four variables. We cannot obtain analytical solutions for either determinacy or E-stability. We therefore rely on numerical simulations to study the properties of the equilibrium. Table 1 summarizes the values we used for the benchmark calibration.

Most parameters are chosen to conform with parameters used in the literature. For example, the discount factor is set at 0.99, the depreciation rate is set at 0.025, and the capital share in production is set at 1/3. The steady state markup is set at a mild level of 1.05, which implicitly defines a value for the elasticity of substitution across intermediate goods, ε. The inverse of the elasticity of labor supply, χ, is set to 1. The curvature of the utility function σ is set to 1 so that the utility is in logarithm form. The fraction of firms that keep their prices unchanged, ω, is given a value of 0.75, which corresponds to an average price duration of about one year. The elasticity of investment with respect to Tobin's Q, η, is set to 1, following King and Watson (1996).
The weights for inflation and output in the interest rate rule, ϕy and ϕπ, and the level of increasing returns θ are left open so we can experiment with different values.
DETERMINACY AND E-STABILITY OF INTEREST RATE RULES
In this section, we study the determinacy and E-stability of REEs under different interest rate rules. Because the results for the four variants of the Taylor rule bear some similarities, our strategy is to closely examine the results for the contemporaneous rule, and then go over the results for the other three variants briefly. To simplify exposition, we use the term “stable REE” to refer to an REE that is both determinate and E-stable, and the term “active policy” to refer to an interest rate rule that responds more than one-for-one to changes in inflation.
Contemporaneous Data Rule
In this section we consider the interest rate rule (19):
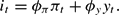
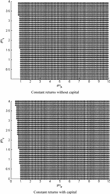
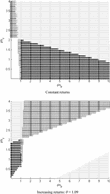
A standard New Keynesian model does not have endogenous capital. Therefore, our first question is whether adding capital alone will change the properties of the equilibrium. To answer this question, we do a side-by-side comparison of a model with capital and a model without. The latter is a special case of the model in Section 2 and is essentially the same as in Bullard and Mitra (2002). In both cases, the production function has constant returns to scale, and we keep all other parameters identical when necessary. We vary the policy weights for output (Y-axis) and inflation (X-axis) and examine the properties of the REE for each combination of the parameters. The results are presented in Figure 1. We use a dark-colored star “*” to indicate that an REE is both determinate E-stable, a square to indicate that an REE is determinate but not E-stable, and a light-colored circle “o” to indicate that an REE is explosive. We left indeterminacy areas blank.

Properties of the REE with the contemporaneous data rule and constant returns. The areas of determinacy and E-stability are marked dark. The areas of indeterminacy are left blank.
The top panel of Figure 1 shows the REE properties of the model without capital. Not surprisingly, the results are identical to those of Bullard and Mitra (2002). When the policy weight for inflation is larger than 1, the REE is always determinate and E-stable. The Taylor principle therefore guarantees the uniqueness and stability of the REE. The bottom panel of Figure 1 shows the results for the model with capital. We note that the stability area nearly coincides with that of the top panel. Most of the determinate and E-stable regions require an inflation weight higher than 1. When the inflation weight goes below 1, the required output weight must adjust upward. Moreover, a determinate REE also must be E-stable, and vice versa, as there is no region denoted by squares or circles. The Taylor principle undoubtedly still guarantees stability in this case. We hence conclude that adding capital alone basically does not change the equilibrium properties of the model. We reiterate that our result is consistent with those of Benhabib and Eusepi (2005), Kurozumi and Van Zandweghe (2005) and Sveen and Weinke (2005).
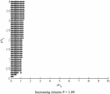
Next, we examine the effect of increasing returns to scale. As a first step, we fix the policy parameters for output and inflation to be 1.5 and 0.5, as originally proposed by Taylor, and increase the level of θ to see if the REE properties will change. We find that when θ is between 1 and 1.05, the REE remains determinate and E-stable. But when θ rises to 1.06, the system becomes indeterminate and E-unstable. This is a first hint that the Taylor principle might not lead to stable equilibria with increasing returns.
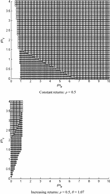
To examine the issue more closely, we next study how the policy parameters ϕy and ϕπ affect the outcomes when increasing returns exist. We fix the level of increasing returns to be 1.09. We choose this number for the benchmark experiment because it is the lower bound of the recent value estimated by Laitner and Stolyarov (2004), and is the upper bound estimated by Basu and Fernald (1994). Other values will be examined shortly. The results are presented in Figure 2.

Properties of the REE with the contemporaneous data rule and increasing returns. The area of determinacy and E-stability is marked dark. The area of indeterminacy is left blank.
The results are striking. With moderate increasing returns, the Taylor principle no longer guarantees stability: the area of indeterminacy and the area of determinacy and E-stability almost exactly reversed when compared with the constant-return case. Although the area of determinacy and the area of E-stability still coincide, this area requires policy weights for inflation that are mostly less than one. Contrary to previous studies, this suggests that an inactive monetary policy is appropriate in terms of stabilizing the equilibrium.
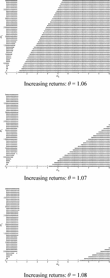
One naturally wonders how the area of stability shifted from the right to the left as the level of increasing returns changes. Next we plot a series of three graphs in Figure 3 to show the transition process. The level of returns to scale starts from 1.06 and increases at an increment of 0.01 in these graphs. We can clearly see that as θ increases, an area of indeterminacy and E-instability is created and gradually expands to the right and wipes off the stability areas on the right. In the meantime, a stable area occurs on the left and slowly expands. The E-stability and determinacy areas always coincide with each other, as in the case of constant returns (there is no area of squares).

REE properties as returns to scale increase from 1.06 to 1.08. The areas of determinacy and E-stability are marked dark. The areas of indeterminacy are left blank.
In Farmer and Guo (1994)'s original analysis of indeterminacy in an RBC model, the required level of increasing returns to generate indeterminacy is quite high (more than 1.2). As we reported earlier, this required level is significantly lower in our model (1.06 for the benchmark calibration). The key difference is that the new Keynesian model allows for price rigidity which links the real marginal cost with inflation (equation 29). As Benhabib and Eusepi (2005) point out, this generates an additional “cost channel” that enhances the effect of inflation expectations on actual future inflation, which makes these expectations more likely to become self-fulfilling than in the flexible price (or RBC) case.
In our simulation exercises, we also find that the steady-state level of markups, denoted by
, significantly affects the required levels of increasing returns to generate indeterminacy. In our benchmark study, we set the markup level to be 1.05. It turns out that if we lower the markup level, the REE is more likely to become indeterminate. We show this finding in Table 2, where all results are obtained by setting the policy weight for output to 0.5 and for inflation to 1.5. When the level of markup is 1.03, for example, an increasing return of 1.04 is enough to generate indeterminacy. When the level of markup is 1.11, the required level of increasing returns is 1.12. This suggests that if an economy has small markups, it is more likely for the REE to be unstable. The intuition is straightforward: the steady-state markup level affects the size of the reaction parameter
in front of the real marginal cost in equation (29). The higher the markup, the smaller this parameter. A smaller reaction coefficient for the real marginal cost reduces the impact of the “cost channel,” which in turn requires a stronger level of increasing returns to generate self-fulfilling equilibria.

The series of results have important implications for policy making. First, it is no longer safe to implement the rule-of-thumb principle of reacting “more than one-for-one” to changes in the inflation rates. As Figure 2 shows, when increasing returns are at a moderate level, the Taylor principle will exactly lead to an unstable equilibrium. Second, the designing of policy rules should condition heavily on the status (level of increasing returns) of the economy. The combinations of policy parameters that lead to determinate and E-stable vary as the level of increasing returns vary. When θ is 1.06 (top panel of Figure 3), a strong response to inflation combined with a weak response to output will almost always guarantee stability, but when θ is 1.09 (Figure 2), such a policy always leads to instability.
In the next three sections, we show that similar results hold for the other three variants of the Taylor rule.
Forward Expectations Rule
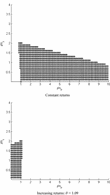
We now turn to the interest rate rule (21):
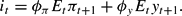
Just as in the previous section, a first experiment shows that when θ = 1.06, the Taylor-suggested policy weights 1.5 for inflation and 0.5 for output no longer guarantee stability. We therefore make a side-by-side comparison of two different REEs, one with constant returns, and the other with increasing returns (θ = 1.09). The results are presented in Figure 4.

Properties of the REE with the forward expectations rule. The areas of determinacy and E-stability are marked with dark stars. The areas of indeterminacy are left blank.
The top panel of Figure 4 displays the results for the case of constant returns to scale. The plot is again almost identical to the no-capital case studied by Bullard and Mitra (2002). Although in general the stability area is smaller than the contemporaneous data case, a more than one-for-one response to inflation combined with a moderate response to output still guarantee the determinacy and E-stability of the REE. The bottom panel of Figure 4 displays the results for the increasing returns case. The conclusion is again reversed. With increasing returns, a less than one-for-one response to inflation is required to obtain determinacy and E-stability of the REE. The smaller stability area compared with the contemporaneous data case shows that an expectation-based rule is in general less desirable.
Lagged Data Rule
We next examine the rule (20):

We present the results in Figure 5.

Properties of the REE with the lagged data rule. The areas of determinacy and E-stability are marked with dark stars. The indeterminate areas are left blank. The determinate but E-unstable areas are denoted by squares. The explosive areas are marked by light circles.
The top panel of Figure 5 shows the results for the constant returns to scale economy. With a lagged data rule, it is no longer true that a determinate REE is always E-stable. Instead, two new areas are introduced. The areas denoted by squares represent determinate equilibria that are not E-stable. The areas denoted by light circles represent REEs that are explosive. While stability seems harder to achieve, it is still true that the Taylor principle basically guarantees determinacy and E-stability, as long as the weight for output is mild enough. The bottom panel shows the results for the increasing returns economy. As before, the small area of determinacy and E-stability violates the Taylor principle and requires a less than one-for-one response to inflation. Active response to inflation leads to either indeterminacy or explosive REEs.
Contemporaneous Expectations Rule
Finally, we examine the economy with the rule (22):
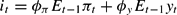
The results are presented in Figure 6.

Properties of the REE with the contemporaneous expectations rule. The areas of determinacy and E-stability are marked with dark stars. The indeterminate areas are left blank. The determinate but E-unstable areas aredenoted by squares. The explosive areas are marked by light circles.
Bullard and Mitra (2002) believe that the contemporaneous expectations rule is both practical and desirable—practical because current data on output and inflation are generally not available but can be estimated, and desirable because it guarantees stability when the policy weight for inflation is larger than 1. This can be seen from the top panel of Figure 6. The large area of stability resides to right of the area where ϕπ is equal to 1. However, as we introduce increase returns, the conclusion no longer holds. As shown in the bottom panel of Figure 6, if we increase the level of θ to 1.09, the area of stability switches to the left, just as in the previous cases we studied. Now an active response to inflation will only lead to indeterminate or E-unstable REEs.
Discussion
When increasing returns are introduced, implementing the Taylor principle often leads to indeterminacy and E-instability. What explains this puzzling result? The key is to understand the role of increasing returns in generating self-fulfilling business cycles.
When Benhabib (1998) first explains the intuition of indeterminacy, he uses the example of sunspot-driven investment booms. When agents expect higher investment returns, they increase investment and accumulate more capital. But with constant returns, the return of investment (marginal product of capital) decreases with more capital accumulation, and the expectations of higher returns will never be self-fulfilled. When increasing returns are high enough, however, more capital will actually increase the return of investment and fulfill the earlier expectations. In our context, this implies that with constant returns, we have the standard increasing marginal cost curve; but with sufficient increasing returns, the firms operates on the part of the marginal cost curve that decreases with the level of inputs.
The rest of the intuition is straightforward. In our model, the monetary authority's job is to dampen any fluctuations driven by inflation expectations. When consumers expect higher inflations, the monetary authority responds by raising the nominal interest rate more than one-for-one with the expected inflation rate. As a result, the real interest rate will rise, which in turn will curb the rise in aggregate demand. With lower demand and a standard marginal cost curve, firms will cut their prices—an action that goes against the earlier expectations of high inflation. This is why the Taylor principle leads to a determinate equilibrium with constant returns to scale. If the firms operate on the decreasing part of the marginal cost curve, on the other hand, lower demand will actually lead them to increase prices, which exactly fulfills the consumers' earlier expectations about high inflation rates. This is why the Taylor principle leads to indeterminacy in the increasing returns case.
Interest Rate Smoothing
Interest rate smoothing has been proposed by the literature to be a desirable policy which is conducive to determinacy and E-stability in models without capital [Woodford (2003); Bullard and Mitra (2003)]. In this section we extend our analysis to include this feature, and obtain some preliminary results. Our job is to examine if the Taylor principle can survive the test of increasing returns when policy smoothing is in the model. We consider the following policy rule:

where ρ∈(0, 1). We experiment with several different combinations of parameter values, particularly for ρ and θ. Our general findings are as follows: with constant returns, the Taylor principle yields determinate REEs as long as the policy response to inflation is not too strong (greater than 6.5% when ρ = 0.5). Moreover, the higher the value for the smoothing parameter ρ, the more likely the REE will also be E-stable under learning. This finding is consistent with the current literature. With increasing returns, the result is again reversed as in previous sections: the REE is more likely to be indeterminate and E-unstable when the reaction parameter for inflation ϕπ is greater than unity. We present a typical result in Figure 7. We therefore conclude that the key mechanism we discussed in previous sections still prevails with policy smoothing.

Properties of the REE with the interest rate smoothing rule. The areas of determinacy and E-stability are marked with dark stars. The indeterminate areas are left blank. The determinate but E-unstable areas aredenoted by squares.
CONCLUSION
This paper incorporates increasing returns into an otherwise standard New Keynesian model with capital. Within this framework, we reexamine the determinacy and E-stability of REE under four variants of the Taylor rule studied by Bullard and Mitra (2002). Although Bullard and Mitra (2002) find that in most cases the Taylor principle is sufficient to guarantee both determinacy and E-stability, we find that with small increasing returns that are consistent with empirical estimates, these findings no longer hold. In particular, some levels of increasing returns require a less-than-one-for-one response of the interest rate rule to inflation to obtain determinacy and E-stability.
The results in this paper suggest that designing the interest rule is much more complicated than simply following a rule of thumb. In our context, a successful interest rule must condition on the level of returns to scale of the economy. There is no reason to believe that the returns to scale of the economy is constant over time. For example, when arguing about the existence of a “new economy,” some researchers point out that the widespread usage of IT technology generates additional externality effect that gives rise to increasing returns. Our results suggest that the monetary authority may well be required to adjust its policy with such changes to ensure market stability.
This paper suggests that the types of interest rate rules that can maintain the stability of the REE are different when there are increasing returns in the economy. Given this result, opportunities now exist for us to study other implications of increasing returns for monetary policy making. In particular, we wonder what effect increasing returns will have when the monetary authority designs its interest rate rules by minimizing a loss function, either with discretion or with commitment. We leave this for future research.
APPENDIX A
In this section, we derive the E-stability conditions for all four variants of the interest rate rules. It is straightforward to show that the white noise shock εt has no impact on the E-stability properties of the system. We therefore ignore this shock in the following calculations. We rewrite the system as
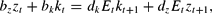
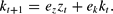
The second equation is derived from the capital accumulation equation that does not involve any expectations.
CONTEMPORANEOUS DATA AND FORWARD EXPECTATIONS RULES
With the contemporaneous data rule and the forward expectations rule, the information sets available for the learning agents are the same, therefore the E-stability conditions are similar. We assume agents have the perceived law of motion (PLM)
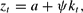
which is in the same form as the MSV solution under REE. The parameter vectors a and ψ will have to be learned. Given this PLM, we calculate the forward expectation of zt as

Plugging this into (A.1), we get

where
. Therefore we obtain the T-mappings:

The REE solution consists of values
and
. The E-stability of
is governed by the local asymptotic stability of the matrix differential equation:

The conditions for expectational stability of the REE solutions are addressed in Evans and Honkapohja (2001, Section 10.3). These conditions are that the eigenvalues of the matrices DT(a) and DT(ψ) all have real parts less than unity. The relevant matrices are as follows:
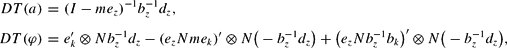
where N =(I−mez)−1 and a and ψ are evaluated at the steady state values.
LAGGED DATA RULE
With the lagged data rule

the implicit assumption is that the agents do not possess knowledge of current data. Therefore, the perceived law of motion must be different. If we plug the interest rate rule into the set of equilibrium conditions, the system becomes

The PLM of the agents is

Given this PLM, the T-mapping of parameters are derived as

The key matrices that determine the E-stability property of the REE are

CONTEMPORANEOUS EXPECTATIONS RULE
With the contemporaneous expectations rule

our implicit assumption about agents' information set is that they do not possess knowledge of current data, and have to use past data to estimate today's output and inflation. We can substitute out the variable yt and rewrite the interest rate rule as

The system can be rewritten as

Plugging the PLM

into the system, the system becomes

Following the similar procedures, we derive the critical matrices as