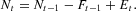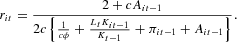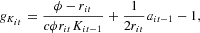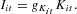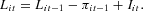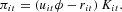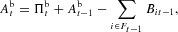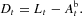INTRODUCTION
In the 1990s a large body of literature—sometimes referred to as the financial accelerator hypothesis, broad credit view, or balance sheet channel—focused on the role of financial factors in business fluctuations and in the transmission of monetary shocks [Bernanke and Gertler (1989, 1990, 1995), Bernanke et al. (1996, 1999), Greenwald and Stiglitz (1988, 1990, 1993), Stiglitz and Greenwald (2003)]. Insightful new additions to the literature, albeit along different lines, have been provided by Kiyotaki and Moore (1997, 2002) and Cooley and Quadrini (2001).
In these models, in principle, agents are heterogeneous, and sometimes it is also recognized that heterogeneity is a necessary ingredient of important business cycle features (such as composition effects), but the nature and consequences of heterogeneity are not thoroughly explored. At a certain point of the analysis, the representative agent pops up and heterogeneity gets lost or is simply neglected.
The temptation to keep the analysis simple by resorting to the representative agent is understandable. After all, the representative agent framework has been one of the most successful tools in economics [Hartley (1997); Stoker (1993)] and is still the cornerstone of standard macroeconomics. This modeling strategy, however, is justified if heterogeneity is temporary, that is, if the population of different households/firms converges over time to a stationary distribution in which agents are identical. This condition is generally not fulfilled empirically. In real economies heterogeneity is not bound to disappear and the evolution over time of the distribution of heterogeneous agents affects the dynamics of the macrovariables. If macroeconomic modeling relies on the representative agent, therefore, the analysis of business fluctuations and of the transmission mechanism of monetary policy will be too simple and sometimes even simplistic.
In this and in a companion paper [Delli Gatti et al. (2005)],1
Previous attempts to cope with the same problem are Delli Gatti et al. (2003) and Gallegati et al. (2003).
To overcome the intrinsic difficulty of dealing with many heterogeneous firms, we adopt the agent-based framework. The evolution over time of microvariables such as the individual level of capital stock, net worth, and output can be tracked by means of simulations. In each period, macrovariables are determined by adding up the levels of the microvariables (bottom-up procedure).
Our model is very simple. Only two markets are considered, goods and credit. In the goods market, output is supply-driven: by assumption, firms can sell all the output they (optimally) decide to produce. Because firms adopt a linear technology whose only input is capital, output follows the evolution over time of the capital stock, which in turn is determined by investment. Finally, investment depends on the interest rate and the degree of financial fragility, which is inversely related to the equity base or net worth. In fact, each firm runs the risk of default, which yields additional bankruptcy costs. The higher the equity base, the lower the probability of bankruptcy and the higher the level of supply and investment.
Firms raise funds on the credit market. The demand for credit is related to investment expenditure and therefore it depends on the interest rate. For the sake of simplicity, we assume that banks are lumped together in a vertically integrated banking sector (“the bank” for short). The supply of credit is a multiple of the bank's equity base because the bank adopts a (spontaneous or enforced through prudential regulation) system of risk management based upon a target equity/loans ratio. Each firm is allotted a portion of total credit proportional to the collateral it can provide, that is, its capital stock. The equilibrium rate of interest for each firm—and therefore its investment and output decisions—therefore depends on the bank's and the firm's net worth.
If a firm goes bankrupt, aggregate output shrinks and the equity base of the banking system is eroded by nonperforming loans or “bad debt.” As a consequence, credit extended goes down, pushing up the interest rate charged to each and every firm. Some of the firms that were on the brink of bankruptcy will default and leave the market, whereas the surviving firms will curtail investment and production. Bankruptcies will spread and a domino or snowball effect will follow.
The source of the domino effect is the positive feedback of bankruptcy on aggregate financial fragility, which in turn is a consequence of the indirect interaction of firms through the banking system: if one firm goes bankrupt, the terms on which the others get credit become more restrictive and their debt commitments become heavier.2
Our model, therefore, is populated by heterogeneous and (at least indirectly) interacting agents in a noisy environment. This scenario recalls the interaction of heterogeneous particles subject to random shocks that is the main theme of statistical mechanics in contemporary physics. In this case, self-organizing phenomena can occur. The theory of self-organized criticality [Bak (1997)] has proved fruitful in many scientific domains and has been applied also in economics [Bak et al. (1993)]. See also Krugman (1996).
The model is extremely simple but capable of replicating through simulations several stylized facts emphasized in the empirical literature:
- the distribution of firms' size is right-skewed and described by a power law [Axtell (2001), Gaffeo et al. (2003)];
- cumulative output changes during expansions and contractions follow a Weibull distribution [Di Guilmi et al. (2003)];
- the growth rate of aggregate and individual output follow similar Laplace distributions [Stanley et al. (1996), Canning et al. (1998)];
- the power law distribution of firms' sizes shifts and rotates over the business cycle [Gaffeo et al. (2003)];
- the age of exiting firms is exponentially distributed [Fujiwara (2003)];
- the distribution of profits follows a power law and is characterized by the time reversal property [Fujiwara et al. (2004)];
- bad debt follows a Weibull distribution [Delli Gatti et al. (2004)].
The rest of the paper is organized as follows. In Section 2 we briefly present and discuss the (optimal) production and investment decisions of the single firm. In the present context, capital accumulation turns out to depend on the financial conditions of the firm, proxied by the net worth of the previous period. Section 3 is devoted to discussion of banks' lending decisions. In equilibrium, each firm is charged an interest rate that depends on the net worth, that is, the financial condition, of the firm and the banking system. Incorporating these results into the law of motion of microvariables such as the capital stock and the equity base of the firms and simulating the model (see the Appendix for the details on the simulation procedure), we can replicate the stylized facts listed above, as shown in Section 4. Section 5 concludes.
FIRMS
In each period, there are a large number—say Nt—of firms. Nt changes over time due to industrial dynamics. Firms produce a homogeneous good using a constant-returns-to-scale technology whose unique input is capital. We assume that the output of the ith firm (Yit) increases linearly with capital (Kit) according to the production function Yit=ϕKit, where ϕ is the productivity of capital, constant and uniform across firms.
In order to simplify the analysis, we assume that production decisions are not constrained by aggregate demand: firms can sell all the output they (optimally) decide to produce.3
Two scenarios are consistent with this assumption. In the equilibrium scenario, aggregate demand accommodates supply; that is, households and firms absorb all the output produced by the latter and the goods market is always in equilibrium. In this scenario, aggregate investment must be equal to the sum of retained profits and households' saving. As we will see, both investment and retained profit are determined in the model, so we have to assume that households' saving adjusts to fill the gap between the two. In the disequilibrium scenario, aggregate demand does not (necessarily) accommodate supply, so that the goods market is generally not in equilibrium. In this case, the difference between aggregate investment on the one hand and the sum of profit and households' saving on the other shows up as involuntary inventories decrease.
Firms differ according to their financial condition. The financial robustness of a firm is proxied by the equity base or net worth Ait.
Firms sell their output at an uncertain price. The individual selling price Pit is a random variable with expected value Pt, the market price, and finite variance. As a consequence, the relative price uit= Pit/Pt is a random variable with expected value E(uit)=1 and finite variance. Moreover, firms are rationed on the equity market and have to rely on banks to obtain external finance. Debt commitments are ritKit, where rit is the interest rate (which will be determined on the credit market; see Section 3).4
Strictly speaking, because Kit=Lit+Ait, debt commitments are ritLit=rit(Kit−Ait). We assume, for the sake of convenience, that firms pay dividends equal to ritAit. Therefore, debt commitments and dividends sum up to rit(Kit−Ait)+ritAit=ritKit.
Profit in real terms is
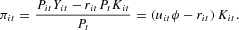
Because of the uncertain environment, firms may go bankrupt. Bankruptcy occurs if net worth at time t becomes negative. The firm accumulates net worth by means of profits. The law of motion of net worth therefore is5
Matter of factly, πit is retained profits. Recalling the definition given in the previous note (Kit=Lit+Ait), in fact, it turns out that πit=uitϕKit−ritLit−ritAit, that is, revenues (uitϕKit) net of debt commitments (ritLit) and dividends (ritAit).
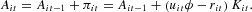
The firm goes bankrupt if Ait<0; that is,
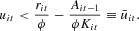
In other words, bankruptcy occurs if the relative price uit falls below the critical threshold
. When a firm goes bankrupt, it leaves the market. The Greenwald and Stiglitz framework, therefore, provides a simple and straightforward way to model the exit process: a firm goes out of the market if its financial conditions are so fragile—that is, its equity is so low—that an adverse shock makes net worth become negative, or if it suffers a loss so huge as to deplete all the net worth accumulated in the past.6
As to the entry process, in the literature, it is modeled either as a purely stochastic process [Winter et al. (1997)] or as an endogenous process [Hopenhayn (1992)] in which the number of entrants depends on the current profit margins. On empirical grounds, we are not able to discriminate between the two views. For the sake of simplicity, in the simulations we model entry as a stochastic process. The number of entrant firms is drawn from a normal distribution. For a detailed discussion and a different modelling of industrial dynamics in Greenwald–Stiglitz models see Delli Gatti et al. (2003).
The probability of bankruptcy is
, where Φ(.) denotes the c.d.f. of uit. Therefore, the probability of bankruptcy is an increasing function of the interest rate and the capital stock and a decreasing function of the equity base inherited from the past. For the sake of simplicity, in the following we assume that uit is distributed uniformly on the interval (0, 2) so that we can specify the probability of bankruptcy as
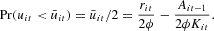
Bankruptcy is costly and the cost of bankruptcy is increasing with the scale of production. For the sake of analytical convenience, bankruptcy costs are increasing and quadratic in the level of output:
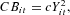
where c is a positive parameter.
Following Greenwald and Stiglitz, we assume that the firm is formally risk-neutral, but it evaluates in each period the probability of bankruptcy and corrects expected profit accordingly. Therefore, the firm's objective function is the difference between expected profit,
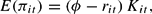
and the cost of bankruptcy in case bankruptcy occurs:
Taking into account (6), (5), and (4) and recalling that Yit=ϕKit, we can formulate the problem of the firm as:7
For high equity ratios the term
is negative. In this case the following objecting function is still valid thinking at this term as a premium for financially solid firms.
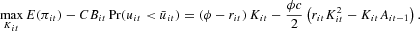
From the first-order conditions (FOC) we obtain
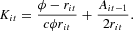
According to (7), the (optimal) capital stock is an increasing linear function of the equity base (lagged one period) and a decreasing nonlinear function of the interest rate. Assuming no depreciation, the law of motion of the capital stock is Kit=Kit−1+Iit, where Iit is investment. The rate of capital accumulation of the ith firm therefore is
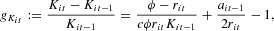
where
is the equity ratio of the firm, an indicator of financial robustness.
Substituting (7) into (1), we obtain
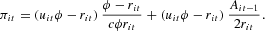
When (9) is substituted into (2), the law of motion of the equity base of the ith firm turns out to be
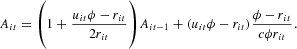
The equity base in period t depends linearly on the equity base lagged one period and nonlinearly on the interest rate.
Because firms raise funds only on the credit market, due to equity rationing [Greenwald et al. (1984), Myers and Majluf (1984)], capital accumulation is financed by means of internal funds (retained profits) and new bank loans; we can write
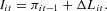
Using the definitions Iit=Kit−Kit−1 and ΔLit=Lit−Lit−1 and substituting equations (7), one obtains the demand for credit of the ith firm,
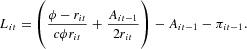
BANKS
For the sake of simplicity and as a first step toward a more satisfactory but necessarily more complex framework, we assume that banks are lumped together in a vertically integrated banking sector (“the bank” hereafter). Therefore many heterogeneous firms interact with only one bank on the credit market.
To determine the supply of credit and its allocation to each firm, let us start from the bank's balance sheet. Without loss of generality, let us assume that there are no reserve requirements. Therefore
where Lt is the aggregate supply of credit and Dt and
represent deposits and the equity base of the bank, respectively.
The bank tries to avoid excess lending by targeting a risk coefficient
—that is, a minimum “capital requirement” of equity (of the previous period) per unit of credit extended—either because of a discretionary strategy of risk management [Estrella et al. (2000)] or as a consequence of prudential regulation on the part of the monetary authorities. Therefore the aggregate supply of credit turns out to be a multiple (1/α) of equity:
Credit has to be allotted to the heterogeneous firms. Because of asymmetric information, the bank does not know the “true” equity of each borrower, but can observe its size, which is used as a proxy for collateral. We assume that the ith firm obtains a portion of total credit equal to its relative size, that is, to the ratio of the ith firm capital stock to the aggregate capital stock (of the previous period),
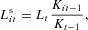
where
. In other words, highly capitalized (i.e., collateralized) borrowers benefit from a large credit flow and vice versa. Hence
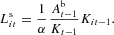
The credit market is in equilibrium when total demand for bank loans is equal to aggregate supply, that is, when the demand for credit of each firm [see equation (11)] is equal to the credit extended by the bank to that firm [equation (12)]. Imposing the equilibrium condition, one gets the equilibrium interest rate:
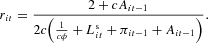
The profit of the bank,
, is the difference between revenues, that is, interest payments on loans extended to solvent firms (
), and costs due to the remuneration of deposits
and of the bank's own capital
:
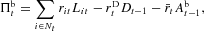
where
is the rate of interest on deposits and
is the rate of return on the bank's equity.
To close the model, we assume that the rate of return on the bank's equity is equal to the average interest rate on loans, that is,
, and that the interest rate on deposits is determined by means of a markdown on the average interest rate, that is,
. Therefore (15) boils down to8
Recalling (12) and (13), interest payments on loans can be expressed in different ways:
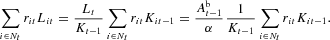
Using the first equality, the average interest rate is
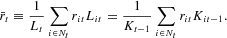
Multiplying both sides of the definition by Lt, one gets
.
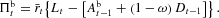
From the balance sheet equation
Moreover,
and
. Substituting these expressions into (16) and rearranging, we get
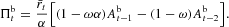
Notice that, by construction, the average interest rate is affected by the equity base (Ait−1) and the relative size
} of the solvent firms and by the equity base of the bank
, which are the determinants of the interest rates on loans extended to the single firms. Therefore, the profit of the bank reflects in a complicated way the financial conditions and the relative size of the borrowing firms and its own financial robustness, captured by the equity base (of the previous periods).
When a firm goes bankrupt, the bank records a nonperforming loan or “bad debt,” which will affect its own equity base negatively. We can define the bad debt as Bit=−Ait if Ait<0, that is, if the ith firm belongs to the set Ft of bankrupt firms. The total amount of bad debt therefore is
.
The bank's equity base evolves according to the following law of motion;
Substituting (17) into this expression and rearranging, one gets
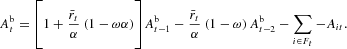
If a firm goes bankrupt, therefore, not only aggregate output but also the bank's equity goes down. As a consequence, aggregate credit goes down, pushing up the interest rate and increasing the risk of bankruptcy for the other firms. Some of the firms that were on the brink of bankruptcy will default and leave the market, and the surviving firms will curtail investment and production. Bankruptcies will spread and a domino effect will follow.
SIMULATIONS
We ran simulations to study the dynamics of the model. There are only four parameters, which are calibrated as follows: ϕ=0.1, c=1, α=0.08, and ω=0.02. Details on the simulation procedure can be found in the Appendix.
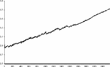
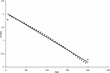
The behavior of aggregate output is shown in Figure 1. Phases of smooth growth follow periods of large output variability; sudden drifts appear from time to time. Each phase of the business cycle has its own amplitude, duration, and depth. There is evidence of asymmetry between expansions and recessions. The standard deviation and autocorrelation of output are 0.27 and 0.79, respectively. The corresponding figures for investment are 1.42 and 0.47.

Aggregate output (in logs).
According to equation (8), growth and fluctuations can be attributed to changes in the equity ratio: the more financially sound a firm is, the more it can invest and grow. Shifts, drifts, and volatility changes, however, can be attributed to the interaction of firms and the banking system. In fact, changes in the firms' and the bank's net worth feed back on the interest rate via the credit market.
Simulations also show that output variance may change over time. This fact can be attributed to changes of the ratio of large to small firms due to interaction and random idiosyncratic shocks. Gabaix (2002) claims that if big firms have a large share of total production, micro shocks will induce large macrofluctuations. In fact, if a large firm goes bankrupt, the aggregate output loss is significant, bad debt spreads through a domino effect and propagates the shock.
We now turn to the stylized facts concerning the shape and evolution over time of the distribution of firms' size, rate of growth, profit and age.
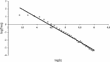
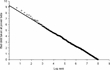
As to firms' size, the empirical literature [Axtell (2001), Gaffeo et al. (2003)] found that the distribution of firms' size is right-skewed and follows a power law. Also, the distribution of firms' size in the simulated data is characterized by persistent heterogeneity and is described by a power law, as shown in the plot of firms' size proxied by the capital stock against the frequency on the log–log plane (Figure 2).
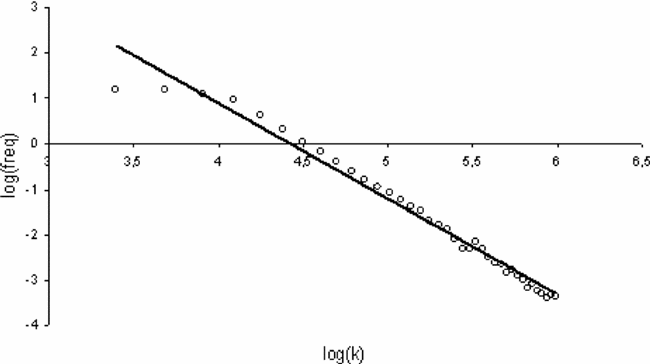
Power law of firms' size.
Gaffeo et al. (2003) found in the data that
- during expansions, the distribution of firms' size shifts to the right—that is, the intercept of the interpolating line in the log–log plane increases;
- the scaling exponent, that is, the slope of the regression line, increases during the transition from recession to expansion.
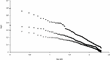
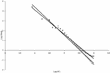
Our simulations replicate these results. The Zipf plots for three different periods of constant growth reported in Figure 3 show the shifting power laws during expansions. In Figure 4 we report the distribution during expansions (circles) and recessions (squares). The slopes of the interpolation lines are 3.30 and 2.60, respectively. Hence, also, for simulated data, the scaling exponent in recessions is lower than in expansions. This means that during upturns concentration goes up.

Distributions for two successive periods of expansion (solid symbols) and a period of recession (empty squares).

Different distributions for firms during expansions (circles) and recessions (squares).
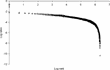
Di Guilmi et al. (2004) found that the plot of cumulative rates of change of GDP for industrialized countries against their rank in a log–log plane is characterized by a large downward curvature, a feature of the Weibull distribution.9
Cumulative rates of change measure the gross change in output over consecutive periods characterized by changes of the same sign (expansions and recessions, respectively).
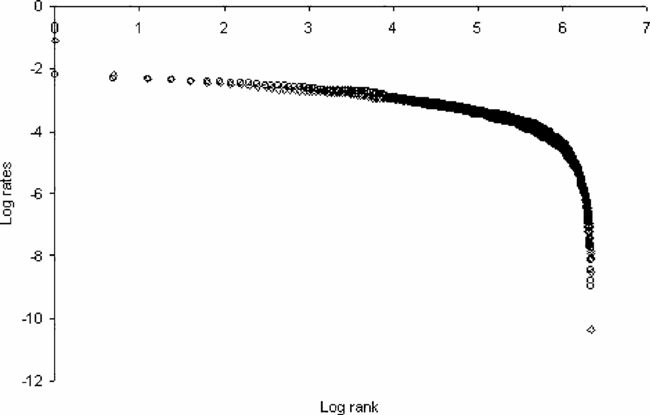
Cumulative rates of changes in output.
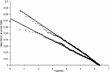
In the same paper, the rates of change during expansions and recessions were interpolated by a Weibull rank regression line, obtaining a good fit. The test of such a distribution for simulated data confirms the reliability of the model (see Figure 6). The fit is very good in both cases (R2 is over 0.99), even if the estimation of the slope parameter returns slightly higher values than the ones found in real data.

Weibull rank regression for rates of expansion (circles) and recession (diamonds).
Canning et al. (1998) found in the data that the distribution of the annual growth rate of GDP is tent-shaped and characterized by exponential scaling. Moreover, Stanley et al. (1996) showed that
- the empirical distribution of firms' growth rates (in the United States) can be approximated by a tent-shaped curve;
- the distribution of the growth rates of firms' size and aggregate output are similar.
In agreement with the evidence reported in the papers above, the rate of change of aggregate output for simulated data follows a Laplace distribution (squares in Figure 7) similar to the distribution of the growth rates of firms' size (circles). The data obtained from our simulations do not collapse onto the same curve: the distribution of firms' growth rates seems to exhibit a slightly steeper slope.

Laplace distributions of output (squares) and capital (circles) growth rates.
Fujiwara (2003) plots the age of exiting firms (in Japan) against the log of their rank. The distribution is exponential, as shown by the good linear fit. We apply the same procedure to simulated data, plotting the ages of exiting firms against the log of their absolute frequency (see Figure 8). The OLS interpolation returns an R2 of 0.99.
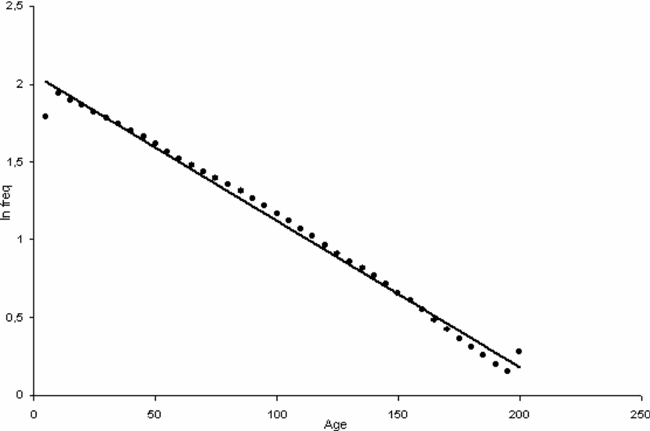
Exponential distribution of firms exits sorted by age.
As widely acknowledged since the pioneering work of Pareto on personal income (1897), firms' operating revenues are also distributed as a power law, with exponent very close to 1. Fujiwara (2003) and Di Guilmi et al. (2003) found in the data that
- the distribution of profits is described by a power law;
- the distribution of profits is characterized by time-reversal symmetry [see Fujiwara et al. (2004)].10
Time-reversal symmetry occurs when the joint distribution of profits in t and t−1 does not change after exchanging the profits recorded in t and t−1 by each firm.
Also, the pattern of the simulated distribution of profits is of the power law type and displays the time-reversal property. The scatter diagram obtained for simulated data shown in Figure 9, in which every point represents a firm, is similar to the ones reported in the above-mentioned papers.

Scatterplot of firms' profits in periods t (x-axis) and t+1 (y-axis).
Di Guilmi et al. (2004) found that bad debt data follow a stretched exponential distribution. Data on bad debt obtained from the simulation (Figure 10) follow a stretched exponential distribution [Laherrere and Sornette (1999)].11
The shape parameter is equal to 0.7654 for simulated data and 0.7060 for real data. In comparing simulated to real data on bad debt, however, a word of caution is appropriate. So far we have used yearly data for firms. Delli Gatti et al. (2004) resorted to monthly data because usually banks record their unpaid credits on a monthly basis. Aggregating the monthly observations of the real data set to obtain yearly data, the two distributions become more similar, because the shape parameter is 0.7658.

Weibull rank regression for bad debt.
CONCLUSIONS
In this paper we have presented a skeletal agent-based model in which the financial fragility of heterogeneous firms and the banking system and their interaction on the credit market play a crucial role in shaping the evolution over time of output, the capital stock, and net worth.
The capability of the model to mimic well-established regularities found in the empirical data is an encouraging signal of a solid microfoundation. Its simplicity notwithstanding, in fact, simulations of the model replicate surprisingly well a whole array of stylized facts: the distribution of firms' size is right-skewed and described by a power law that shifts and rotates over the business cycle; cumulative changes of output during business cycles follow a Weibull distribution; the rates of change of aggregate and firms' output follow a similar Laplace distribution; the distribution of the age of exiting firms is exponentially distributed.
The model can be extended in a number of ways to take into account, among other things, the role of aggregate demand, different degrees of market power on the goods and credit markets, policy variables, and learning processes. Our conjecture, however, is that the empirical validation of more complex models will be due to basic ingredients already present in the benchmark framework: non-linearities, random idiosyncratic shocks, and changing financial conditions of interacting firms and banks.
APPENDIX: SIMULATION PROCEDURES
In this Appendix we briefly describe assumptions and procedures followed to run the simulations. A simulation is completely described by the parameter values, the initial conditions and the rules to be iterated period after period.
First of all, we set the parameter values and the initial conditions for state variables needed to start the simulation. There are only four parameters in the model: the productivity of capital ϕ, the parameter of the bankruptcy cost equation c, the bank's equity-loan ratio α, and the markdown on interest rate ω. They are set as follows: ϕ=0.1; c=1; α=0.08; ω=0.002.
The first step of the simulation occurs at time t=1. To perform calculations in period 1 for each firm we must set initial conditions for firms' capital, the equity base, loans, profit, and bad debt: Ki0, Ai0, Li0, πi0, Bi0. We chose the following:
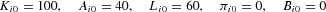
These initial conditions are uniform across firms. Therefore in period 0 firms are identical. The degree of financial robustness as measured by the initial equity ratio is ai0=0.4. We set the initial number of firms at N0 = 1,000.
We must set initial conditions also for the bank. Aggregate credit supply is
. From the definition of credit supply,
, we can derive the equity base of the bank in period −1,
. We assume also that
, so that
Therefore we can also set
From t=1 on we have the following list of operations:
- Bankrupt firms in t−1 exit the market. Their number is Ft−1.
- New firms enter the market. Their number Et is drawn from a normal distribution with mean μE and variance . They are given the initial conditions as in (A.1). The number of existing (surviving and entrant) firms is

- The bank determines the total supply of credit according to

- Each firm is charged the interest rate
This expression reflects equilibrium between demand and availability of credit for each firm (see note 8).

- Each firm determines the optimal rate of capital accumulation [see equation (8)],
and investment,


- Each firm determines the demand for loans,

- Each firm is hit by the idiosyncratic shock. Therefore profits are

- The bank calculates the profit,

- The bank calculates its equity base,
and deposit,


- Each firm determines its net worth,

- Each firm is checked for bankruptcy. The number of bankruptcies (Ft) is determined. Bad debt is calculated according to

- All the available data (from surviving and bankrupt firms and the bank) are recorded. We are ready for the next period loop starting again from 1.