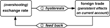INTRODUCTION
The seminal overshooting model of Dornbusch (1976) has been a key reference regarding the long-run neutrality of money for the last twenty-five years. Monetary shocks are assumed to affect real variables in the short run while prices are sticky, but the shocks are neutralised as prices adjust—and the real effects decay over time. The economic turbulence of the 1980s, with large exchange rate misalignments, questioned the validity of the long-run neutrality hypothesis. Several authors claimed that economic systems could contain hysteresis, making economic processes path-dependent and to some extent invalidating the reasoning based on unique long-run equilibrium (e.g., Layard et al., 1991; Soskice et al., 1989). At first, the hysteresis approach gained recognition within labor market theories (Lindbeck and Snower, 1988; Gottfries and Horn, 1987), but after some time it was introduced to economics in general. The relationship between foreign trade and exchange rates was one of the new extensions of this theory.1
For an overview of hysteresis in economics, see Cross and Allan (1988), Cross (1993), Franz (1990), or Göcke (2002).
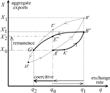
Of course, there is an interaction between both phenomena, that is, exchange rate fluctuations or overshooting, on the one hand, and persistent hysteresis effects in foreign trade, on the other hand. A temporary exchange rate misalignment will induce persistent effects on the current account (hysteresis effect

in Figure 1) and this persistent change in the current account will alter the equilibrium level of the exchange rate (feedback effect
in Figure 1).

Interaction between exchange rate and hysteresis in foreign trade.
Baldwin and Lyons (1994) explicitly integrated a model of hysteresis in foreign trade into an overshooting model, and showed how hysteresis in such a case could be transferred back into the exchange rate process itself. However, they applied a concept of hysteresis on a macroeconomic level that is equivalent to the microeconomic hysteresis behavior of a single exporting firm.
2Ljungqvist (1994) illustrates this feedback effect of microeconomic hysteresis in a general equilibrium model.

is modeled inadequately via a microeconomic type of hysteresis, the resulting feedback effect
on the exchange rate may be an insufficient description of the exchange rate process on a macroeconomic level.
Based on panel data sunk cost hysteresis has been corroborated by several studies on a micro-firm level, for example, by Roberts and Tybout (1997) for Colombian exports; by Giovannetti and Samiei (1996) for Japanese exports; by Máñez et al. (2004), Campa (2004), and Martinez-Zarzoso (2001) for Spanish exports, by Bernard and Wagner (1998) for German exports, and by Bernard and Jensen (2004) for U.S. manufacturing exports. Remarkably, in these empirical studies the heterogeneity effects between firms are identified. Hence, the consequences of heterogeneity should be taken into consideration in theoretical modeling.
Amable et al. (1991) and Cross (1994) introduced a Mayergoyz (1986)-aggregation procedure into economics, explicitly deriving a continuous nonlinear macroeconomic hysteresis loop. The aggregation procedure is based on heterogeneous firms each with a microeconomic noncontinuous market entry/exit switching behavior. In this approach, persistence comes about continuously with every change in the direction of the input path. The passing of extreme trigger values (i.e., a “large” exchange rate shock) is not necessary any more in order to introduce persistent effects.3
For the implementation of macro hysteresis into a Branson portfolio balance model, see McClausland (2000). See Göcke (2001) for an integration of a linear approximation of macro hysteresis in a Mundell-Fleming-type model. Hule (2000) implements an alternative type of hysteresis (with a pattern similar to mechanical play) into a Dornbusch overshooting model. Another common way to model persistence effects is via difference (differential) equations showing unit (zero) root dynamics. See O'Shaughnessy (2000) for a recent example. The inadequacy of unit-root dynamics as an approximation to the nonlinear hysteresis-dynamics is discussed in Amable et al. (1993, 1994). For an overview of the variance in interpreting the term “hysteresis” in economics, see Göcke (2002). For a detailed mathematical analysis of various forms of hysteresis, see Krasnosel'skii and Pokrovskii (1989) and Brokate and Sprekels (1996).
This paper integrates an overshooting model with such a continuous macroeconomic hysteresis loop in a simple way, deriving a path-dependent relationship between the exchange rate and foreign trade. The model shows how sticky prices and overshooting effects provide a framework in which persistence can occur continuously in an economy, and not only as extreme trigger values of the exchange rate are realised. Moreover, because of the continuous nature of macroeconomic hysteresis, a variable amount of interaction between the hysteresis effect and exchange rate overshooting is shown to exist: the stronger the overshooting, the more severe the persistent effect is on the new long-run equilibrium exchange rate. In addition, the degree of overshooting is reduced by the degree of persistence: The higher the persistence, the weaker the overshooting impact effect on the exchange rate. Hence, the long-run persistent effects in foreign trade dampen the short run exchange rate fluctuations in general. In addition, we will show that hysteretic effects introduce a violation of the long-run neutrality of money, as long-run effects on the equilibrium real exchange rate are induced; that is, Purchasing Power Parity (PPP) is violated, in contrast to the situation of the original Dornbusch (1976) overshooting model.
The paper first repeats the hysteresis concept in foreign trade on the microeconomic level, as well as an adequate aggregation approach. In Section 3, a combined overshooting and hysteresis framework is set out, in which the persistent effects of a monetary policy are analyzed. A numerical simulation is conducted in Section 4 and the last part draws the conclusions of the paper.
HYSTERESIS IN FOREIGN TRADE
Discontinuous Hysteresis Effects on a Microeconomic Level
Hysteresis is a property of open dynamic systems in which effects of past values of the explanatory variable remain behind. In foreign trade, persisting consequences of temporary exchange rate shocks on quantities and prices can be a result of the existence of sunk market-entry costs.4
For models with sunk-cost hysteresis in foreign trade, see, for example, Baldwin (1989, 1990), Dixit (1989, 1989a), Giovanetti and Samiei (1996), Göcke (1994), Han (1991), Harris (1993), Ljungqvist (1994), and Roberts and Tybout (1997). For other reasons of hysteresis in foreign trade, see, for example, Froot and Klemperer (1989).
For a thorough discussion of the theory on the relationship between exchange rates and tradable goods prices, see Goldberg and Knetterer (1997).
An incomplete exchange rate pass-through is presumed, that is, the foreign prices for exported goods do not change in proportion to the exchange rate variation. Thus, for exchange rate alterations, the exporting firms have to bear revenue changes in their own currency. For a model explaining this pricing to market behaviour based on a long run optimization, see Borgersen (2001).
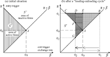
Because hysteresis effects are based on the decisions of single firms, foreign trade hysteresis is mainly examined in a microeconomic framework. At the microeconomic level, hysteresis implies a difference between the exchange rates, which trigger market entry and exit of potentially exporting firms. The path-dependence occurs discontinuously when “passing” the respective rates. This pattern is illustrated in Figure 2.7
For a more detailed derivation of the entry/exit triggers (corresponding to the modeling of exchange rate expectations as applied in the next section of this paper), see the appendix A.
This is referred to as the “hysteresis band” by Baldwin (1988).
See Hule (2000) for a sophisticated definition of irreversibility.

Discontinuous microeconomic hysteresis loop for asingle firm j.
The microeconomic exporting behavior of a single firm (as illustrated in Figure 2) is determined by a noncontinuous hysteresis loop (characterized as a “nonideal relay”). The qualitative characteristics of this stylized pattern remain the same if the optimisation problem of the firm is extended to a multiperiod optimization, including consideration of the advantages of current activity for future costs. Even a situation with uncertainty—introducing an option value of a “wait-and-see strategy”—will result in the same shape of the supply pattern. However, the option value effects will amplify the core sunk costs of entry or exit and lead to a widening of the band-of-inaction, thus reinforcing the hysteresis property (Dixit, 1989, 1989a; Belke and Göcke, 1999).
Aggregation and Hysteresis on the Macroeconomic Level
In this section, we give a brief outline of the Mayergoyz (1986) aggregation procedure, which allows an aggregation of heterogeneous single firms, each characterized by a micro hysteresis loop, resulting in a continuous macro loop of overall exports.10
For a more detailed description of the aggregation procedure, see Amable et al. (1991, 1994), Cross (1994), or Göcke (1994).

Active (heterogeneous) firms dependent on the exchange rate.
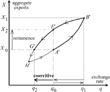
Assume an initial situation in point A [in Figure 3 (a)] with a preceding time path of the exchange rate that has created an area containing all actively exporting firms S+ (and, correspondingly, an area of inactive firms S−). The area of S+ summarizes the aggregate exports X of the economy. As a simplifying assumption, S+ has an upper borderline toward S− with a negative slope equal to one and the heterogeneous firms are assumed to be continuously distributed in the α≥β-triangle.11
The simplifying assumptions concerning the initial shape of S+-borderline and on the distribution of heterogeneous firms in the α>β-plane are not crucial for the essential qualitative features of the aggregate macro-hysteresis loop. However, the curvature of the macro loop depends upon the distribution of the firms. Under the assumption of continuously distributed firms, a continuous macro loop can be derived. For a derivation of the macro loop under more general assumptions, see, for example, Amable et al. (1991, 1994).
With an increase in the exchange rate from
(i.e., for a depreciation of the domestic currency), some previously inactive firms will enter the foreign market. This reaction is represented in Figure 3 (b) by an expansion of S+ by the triangle ABC (i.e., by an upward shift of the horizontal S+−S−-borderline CB). A subsequent reversal of the exchange rate back to the initial level
results in an exit of the firms represented by the triangle ABE (along the vertical line AE). Although the exchange rate has regained its initial level, some firms that have entered the foreign market during the period of depreciation, will stay: the triangle AEC represents this persistent macroeconomic remanence effect. In order to obtain the initial level of aggregate exports X0, a further decrease beyond the initial exchange rate is necessary. For q2 the triangle AFG of initially active firms, which subsequently have left the market, is compensated by the triangle area FDC, which represents remanent firms that have entered during the depreciation but that have not yet reexited. This extra change (q2−q0) of the forcing variable, which exceeds the reversal of the impulse, is called (analogously to magnetics) the “coercitive (force).” The size of this coercitive force depends on two factors: (1) the magnitude of the initial impulse (
, and (2) the distribution of (potentially) exporting firms in the α≥β-triangle. In the particular case of equally distributed firms (and, additionally, with every firm representing the same amount of exports), a direct geometrical interpretation is possible: the area of the triangle AFG must be identical to the area of FDC in order to determine the coercitive extra change (q2−q0). However, in a more general case, the size of AFG and FDC need not be identical. If, for example, the majority of firms faces moderate sunk costs, the region near to the 45° line (e.g., AFG) is “populated” more densely compared to the more “outlying” northwestern region (e.g., FDC) representing very hysteretic firms with high sunk costs. In this case, a relatively small geometric area of AFG represents a huge amount of exports. Thus, a small AFG could compensate a geometrically large FDC triangle, which—as a result of a low population density—represents the same amount of exports. In such a case, the coercitive (q2−q0) is small compared to the initial impulse (
. In the opposite case of a very hysteretic economy with a higher population density in the northwestern area (e.g., the majority of firms confronted with severe sunk costs), AFG must be geometrically larger than FDC in order to represent the same export weight. Consequently, in this case, the coercitive must be large compared to the initial impulse.
The effects of the exchange rate sequence
on aggregate exports are depicted in Figure 4. The initial impulse
leads to an increase of exports of
. The exchange rate reversal
results in a level of export of X2>X0, that is, a hysteretic remanence effect (X2−X0) occurs. In order to reach the initial export level X0 the exchange rate has to attain q2<q0, with the difference (q2−q0) being the coercitive force.12
A reversal of the effects of the temporary exchange rate alteration requires an even further decrease of the exchange rate, as depicted with the path G′H′A′ in Figure 4.

Continuous macroeconomic hysteresis loop.
The differences between the micro loop in Figure 2 and the aggregate macro loop in Figure 4 are obvious. In the case of micro hysteresis, only two states are possible. A jump between these two noncontinuously linked equilibria only occurs with the passing of certain thresholds. The continuous macro loop results from aggregation over a high number of heterogeneous micro elements. Because of the lack of thresholds and discontinuities, even small changes in the exchange rate can have durable effects on the aggregate level.
In the special case of not only continuously but also equally distributed firms in the α≥β-triangle, we have a one-to-one correspondence between aggregate reaction and the corresponding geometrical area. Thus, a direct geometrical interpretation of the rectangular triangles ABC, ABE, AFG, and FDC is possible in this case: an application of the theorem of Pythagoras results in the following relation between the initial impact (q1−q0) and the coercitive force c1=(q2−q0):13
See Appendix B for the derivation.
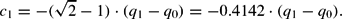
However, under more general distribution assumptions, the factor/relation between c1 and (q1−q0) would be different and generally not constant with respect to the size of (q1−q0). In the following we will apply a more general formulation of the coercitive effect but remain with the (simplifying) linearity assumption, through a constant factor χ relating the coercitive to the initial impact:14
In the case of a very hysteretic economy with a relatively high population density in the northwestern region, we would expect a parameter χ>0.4142; and in the opposite case of an economy based on a majority of firms with moderate sunk costs we would expect χ<0.4142.
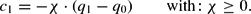
So far, the logic of micro- and macro-hysteresis is explicitly outlined only for the domestic exporters. Of course, an identical logic applies for the domestic imports, that is, for foreign firms considering to enter or to leave the domestic market in the presence of sunk costs. Hence, the statements concerning the qualitative features of the aggregate export loop will also apply for the aggregate imports of a country. Thus, of course, the impulse and coercitive force relation in (2) can be applied to the entire current account as well.
By including the macro-hysteretic relationship into a macroeconomic overshooting model, the effect of temporary fluctuations on the long-run equilibrium exchange rate can be derived. The model allows for a path-dependent current account impact on demand, prices, and exchange rates, invalidating the hypothesis regarding the long-run neutrality of money.
THE OVERSHOOTING MODEL CONTAINING HYSTERESIS IN FOREIGN TRADE
The Money and the International Capital Market
Our starting point is a conventional sticky price model along the lines of Dornbusch (1976). We assume a small open economy, facing a given world market interest rate and perfect capital mobility. The interest parity condition is assumed to hold. The hysteresis model explains the foreign trade structure of the economy, that is, the dynamic relationship between real exchange rates and the current account is characterized by a macro-hysteresis loop, as illustrated in Figure 4. Because hysteresis is at first a goods market phenomenon, the description of the money and capital market remains the same as in Dornbusch (1976). Hysteresis is introduced to the model via the goods market but shows repercussion effects on the equilibrium of the other markets.
The money market determines the domestic interest rate and is described by a conventional equilibrium condition, where the real money supply (M/P) equals the real money demand. Demand is increasing in real income (Y) and decreasing in the interest rate (r). Small letters represent natural logs. To keep the notification simple, an explicit time index ‘t’ is suppressed. The equilibrium condition equals:

In order to capture domestic price effects, the nominal spot exchange rate e (as log of the nominal price of foreign exchange), and the log of the real exchange rate q is explicitly distinguished. The world market price is assumed fixed (and normalized: ln(P*)=0), so that the real exchange rate is equal to:
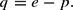
The expected rate of nominal depreciation is adaptively adjusted with reference to the steady state equilibrium
. Note that in the case of hysteresis, the equilibrium is not unique but path-dependent. This is the essential difference to the original Dornbusch (1976) overshooting model. The expected rate of exchange rate depreciation
is assumed to be proportional to the discrepancy between the actual rate and the long-run equilibrium exchange rate. The speed-of-adjustment coefficient θ is (for the moment) exogenously given:
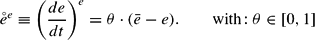
Capital mobility is characterised by an interest parity condition that implies perfect substitutability between assets denominated in domestic and foreign currency. The interest rate is approximated by r≈ln(1+i). The world market interest rate is given by r*, and is fixed due to the small country assumption.
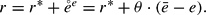
Combining equations (3), (5), and (6) leads to a relationship between the nominal spot rate, the price level and the long-run equilibrium exchange rate, given the money market clearance and the asset market equilibrium condition:
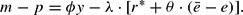
In the long-run equilibrium, expectations are correct (
) and the expected rate of depreciation is zero, making the domestic interest rate equal to the world market interest rate (r=r*). Thus, the steady state price level is:
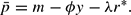
The combination of equations (7) and (8) results in:
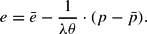
Thus, the nominal exchange rate is determined by the price level. The price determines the interest rate via the real money supply; and via interest parity the nominal exchange rate is set.
The Goods Market Containing Hysteresis in Foreign Trade
Now we have to implement hysteresis effects into the goods market. The goods market is characterized by a real income, which is fixed by the supply side (y= const.).15
Later in this paper, we will show that the equilibrium real exchange will show hysteresis effects. Of course, a shift in the terms of trade has an effect on the value added by the economy (i.e., on output y). As a simplification, these effects are neglected and the output is assumed to be constant.
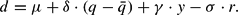
The inflation rate
is assumed to be proportional to an excessive demand factor:
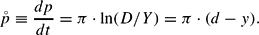
An exogenous shock, which leads to a temporary deviation from an initial equilibrium level of the real exchange rate
, will result in a new equilibrium level
provided that hysteretic remanence effects on the current account occur. The difference between the old and the new equilibrium of the real exchange rate is given with the coercitive force c1. It guarantees that the initial (equilibrium) level of the current account will be regained in the new steady state. The real exchange rate in the first moment after the shock (t=+0)—that is, the overshooting exchange rate after the impact effect—is stated as q1. Hence, the initial impulse is (
) and the new equilibrium level of the real exchange rate is:
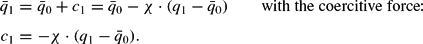
The real demand after a shock is
. Thus, the change of the price level is now given as:
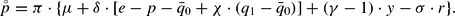
An actual remanence and coercitive effect as stated in (12) requires a real entry or exit of exporting firms into the foreign market. Thus, although the supply is fixed, the current account is not. When q rises in the course of a real depreciation, firms will enter the foreign market, as the real exchange rate change brings about a rise in unit revenues converted into the home currency. At the same time, the unit revenue on the domestic market, that is, the price, is sticky and lags behind.16
The world market price is assumed constant (and normalized), that is, concerning the foreign market a “total pricing-to-market” of domestic exporters is assumed. Thus, converted in domestic currency the (log nominal) unit revenue of exported goods is the nominal exchange rate e. Hence, the real exchange rate q states the relation of unit revenues of foreign sales compared to domestic sales. Without any frictions the unit revenues would be equal on both markets (this would be the PPP-case). However, because of sunk-market entry costs, unit revenues on the foreign market e must exceed p in order to lead to market entries; and because of sunk-market exit costs p must exceed e for market exits. In contrast to the foreign price level, the domestic price is not constant but reacts in a sticky way. This pattern is a result of some kind of adjustment costs, which are not addressed explicitly in this paper. However, the smooth and monotonous adjustment process of the domestic price cannot be based on fixed sunk costs but on a convex adjustment cost technology, leading to a delayed adjustment but not to permanent deviations. This is in contrast to the foreign market, where fixed sunk adjustment costs result in permanent effects. For a discussion of different types of adjustment costs and pricing-to-market, see Kasa (1992).
In the long run, a goods market equilibrium implies
. With r=r* the new long-run equilibrium of the nominal exchange rate after a shock (
) is under consideration of the coercitive characterised by:
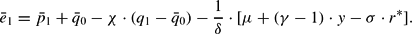
Using (12), the definition of the new equilibrium of the nominal exchange rate
can be reformulated with explicit consideration of the coercitive. In the first moment after the shock the nominal exchange rate “jumps” to e1 while the price level is sticky and, for the present, remains on its initial level
.
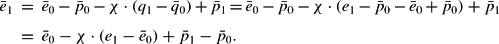
Reformulating (9) yields:
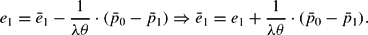
Equating (15) and (16) gives the instantaneous jump of the nominal exchange rate directly after the shock:
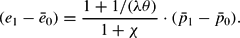
The price dynamics can be derived from (13), by inserting e1 as implicitly given in (17), and using
corresponding to (14), by substituting e as stated in (9), and under application of the definition equations q1=e1−p1 and
as well the sticky price condition
. The result shows that the price dynamics are described as an autonomous first order differential equation of the form
; that is, the only endogenous variable that determines the change of the price is the price level itself.
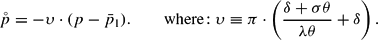
Equation (18) is equivalent to Dornbusch's (1976, p. 1165) equation (10). However, the interpretation is different. As a result of hysteresis effects, the new equilibrium level
is different compared to a situation without hysteretic coercitive effects (i.e., when χ=0). In a situation without hysteresis, the equilibrium level of the real exchange rate (which determines the long-run level of p and e) is unique; that is, long-term changes of the nominal variables e and p must be proportional and no real effect will occur in the long run. Thus, monetary shocks are neutral in the long run. However, in a situation with hysteresis in foreign trade (χ>0), the long-run effects on p and e are not proportional, as the real exchange rate q changes. Hysteresis implies long-run non-neutrality of monetary disturbances and the violation of Purchasing Power Parity even in the long run.
The solution of (18) is straightforward (under consideration of the initial condition
):
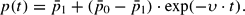
Substitution of p(t) in (9)
[with:
] gives the time path of the nominal exchange rate:
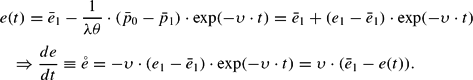
Rational Expectations
A perfect foresight path requires the actual exchange rate dynamics
to equal the expected rate of nominal depreciation as stated in (5). Thus, the adaptive model shows rational expectations if the following constraint applies to the adaptive expectations coefficient θ (Dornbusch, 1976, p. 1167):
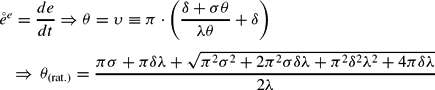
A Monetary Shock
As an example, we will now discuss the effects of a monetary shock. The money supply is increased once, from an initial level m0 to m1 by an increment dm≡m1−m0. According to (8) the long-term equilibrium price level shows a change that is proportional to the monetary shock:

Inserting this long-run price effect into (17) gives the impact effect on the exchange rate, that is, the jump in the first moment after the monetary shock:
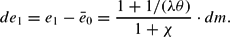
Because the prices are sticky, the real exchange rate jump equals the nominal impact effect in the first moment after the shock (
. As can be seen from (23), an interaction between hysteresis effects and exchange rate overshooting exists. The higher the hysteretic coercitive effects (the higher χ), the lower is the new long-run equilibrium rate of the real exchange rate
and, thus, the lower is the first period jump of the exchange rate (dq1=de1) immediately after the shock. Hence, the overshooting of the exchange rate is reduced via long-run coercitive force effects introduced by hysteresis in foreign trade. For χ=0, our (23) reduces to Dornbusch's (1976, p. 1169) equation (16).
With (15), (22), and (23), the hysteretic long-run equilibrium effect on the nominal exchange rate can be calculated:
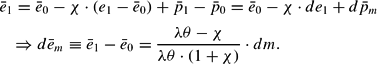
In a situation without hysteresis (χ=0), we have a proportional long-run effect on the nominal exchange rate (
), and, thus, for χ=0 there is no long-run effect on the real exchange rate q—that is, as a result of long-term monetary neutrality the PPP holds. However, in a situation with hysteresis effects in foreign trade (χ>0), the monetary expansion has a long-run effect on the real exchange rate. The real depreciation in the short run ultimately results in a real appreciation in the long run (for dm>0⇒dq1>0 and
):
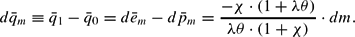
A Graphical Illustration of the Dynamics
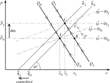
The dynamics of the hysteretic system can be illustrated by a two-dimensional (e, p)-plane using the phase diagram technique (see Figure 5).17
For the corresponding graph in a situation without hysteresis effects, see Dornbusch (1976, p. 1169).
) the line QQ represents the stable saddle-path of the system. To illustrate the point more fully the (
)-isokline, as implicitly given in (9), and the (
)-isokline, as derived from (13), are depicted. The initial equilibrium situation is represented by point A. As the monetary expansion has a positive long-run effect on the price level and as the real exchange rate is reduced in the long run by the temporary devaluation, the 45° line characterizing a constant real exchange rate based on its definition (
) is shifted to the left, because of the hysteretic coercitive force. This dampens the impact effect on the exchange rate. The short-run impact effect in Figure 5 is shown via the jump from A to point B. The adjustment to the new long-run equilibrium (from B to point C) takes place along the new saddle-path Q1Q1.18
If
were the unique equilibrium PPP level of the real exchange rate in the standard case without hysteresis, the monetary shock would result in a jump to point D in Figure 5. Subsequently, the transitional dynamics toward the unique
-equilibrium line in point E would take place on the saddle-path DE.

Effects of a monetary expansion in a phase diagram.
A NUMERICAL EXAMPLE
The process of hysteresis and the persistent real exchange rates can be illustrated by a simulation of the model. The parameters of the model are set to χ=0.4, π=0.5, δ=3, σ=4, μ=1, λ=4, ϕ=0.25, γ=0.8. The initial situation in the economy is given as m0=1, y0=1, r*=0.1, e0=1. The economy is assumed to be in equilibrium initially, where the money market is given as
and
. The rational expectation coefficient
equals the price adjustment coefficient υ:
. Both the level of production and the foreign interest rate are assumed fixed—that is, dy=dr*=0.
Consider a monetary expansion equal to dm=m1−m0=0.5. The new equilibrium price level is
, and the nominal exchange rate immediately before the monetary shock (in t=−0) is e0=e(t=−0)=1. In the first moment after the shock (t=+0), it equals e1=e(t=+0)=1.398239034. The new long-run equilibrium exchange rate is
, making the first moment overshooting over its long-run equilibrium level equal to
. The differential equations reflecting the speed of adjustment of the price level and its solution can be calculated as:

The slow price adjustment and the excessive overshooting of the nominal exchange rate initiated by the monetary expansion are illustrated in Figure 6. Corresponding to the stylized representation in Figure 5, the simulated saddle-path dynamics are depicted in a standard (e,p)-diagram in Figure 7. Additionally, the time path is explicitly given in an (e, p, t)-3D-plot.

Reaction of the sticky price level p and of the overshooting nominal exchange rate e on a monetary expansion.

Saddle-path dynamics of the price level and the nominal exchange rate.
In the new long-run equilibrium
and
, the total equilibrium effect on domestic prices, the nominal exchange rate, and the resulting negative long-run effect on the real exchange rate are:
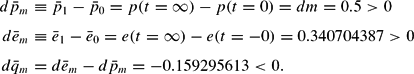
These results imply that with a monetary expansion the price effects are neutral in a conventional sense. However, because there is an underproportional nominal exchange rate depreciation, the exchange rate shows nonneutral effects. The combination of these two nominal effects produces a real exchange rate effect, which makes the monetary shock nonneutral in the long run. Although in the short run a real depreciation takes place, the real exchange rate appreciates in the long run.
CONCLUSION
The overshooting model of Dornbusch (1976) is often used to show the consequences of short-run exchange rate fluctuations in a situation when the long-run neutrality of money hypothesis holds. The combination of sticky prices and flexible asset markets produces real effects in the short run, but as prices adjust these effects decay over time. However, we present a Dornbusch type model with sticky prices and overshooting exchange rates where long-run hysteresis effects in foreign trade flows can come about. For instance, a short-run (overshooting) depreciation leads to an entry of some domestic firms on the foreign market, which, because of sunk-entry/exit costs, is not easily reversed. These market entries result in a remanent positive effect on the current account. Because of the feedback on the exchange rate process, this ultimately induces a long-run equilibrium appreciation of the real exchange rate. In analogy to the concept of hysteresis in magnetics this effect is called “coercitive (force).” Consequently, an expansionary monetary shock that leads to a temporary exchange rate depreciation eventually will be followed by a persistent appreciation (i.e., the coercitive effect).
In our model, the hysteresis effects are based on a continuous hysteresis loop as typical for macroeconomic relations based on heterogeneous microeconomic agents. Thus, in contrast to the microeconomic pattern of hysteresis as applied in Baldwin and Lyons (1994), in our model passing of extreme trigger values is not necessary in order to produce remanent effects on an aggregate macroeconomic level. From a technical point of view, the hysteretic coercitive effect on the long-run equilibrium level of the real exchange rate is introduced into the original Dornbusch model in a very simple way—via merely adding a single extra parameter χ, which describes the (inverted) relation between initial overshooting and the long-run coercitive effect. Moreover, our model exhibits an interaction between the long-run coercitive equilibrium effects and the short-run overshooting exchange rate fluctuation. First, the more severe the overshooting, the bigger the persistent effect is on the long-term equilibrium. But, simultaneously, the coercitive equilibrium effect induces a feedback on the size of the initial short-run overshooting. Consider again a monetary shock that leads to a temporary exchange rate depreciation, which is followed by a persistent equilibrium appreciation. The expectation of this long-run equilibrium appreciation already dampens the initial overshooting depreciation. Thus, the stronger the long-run persistence effect (i.e., the larger the coercitive parameter χ), the weaker the initial exchange rate “jump” is. So it can be said that introduction of a path-dependent variation in the long-run equilibrium dampens the short-run fluctuations of the exchange rate.
As short-run fluctuations can cause long-run effects on the real exchange rate, even in the long run the neutrality of money is invalidated in our model. Because there is no unique level of the equilibrium real exchange rate, but a path-dependent equilibrium, naturally, PPP is also invalidated. It should be noted that the process of overshooting and the resulting coercitive force leading to a new equilibrium is connected to social costs19
In magnetism the corresponding actions result in a loss of energy in the form of heat.
See Roberts and Tybout (1997) for a thorough policy discussion.
APPENDIX A
Determination of Entry and Exit Triggers, Adaptive Expectations, and the Size of the Coercitive
If an unexpected shock has taken place, an adaptive adjustment process to the (new) long-term equilibrium
is expected. Note that, because of hysteresis effects, the long-term equilibrium
is changed in the course of the shock. The combination of equations (5), (18), and (21) leads to:
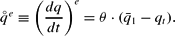
If a previously inactive firm j enters the market it has to bear sunk entry costs Hj>0. Revenues in domestic currency are a positive function of the relative price of foreign exchange. For simplification, let this positive effect of exchange rate on revenues simply be expressed by q (i.e., the log of the real exchange rate). The variable costs for our firm are εj. Thus the instantaneous profit for the firm is (qt−εj). In the case of an entry directly after a shock (with a temporary exchange rate extremum qt=q1), the expected present value of firm j can be calculated under the application of the (constant) interest rate r*:
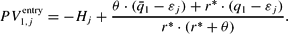
For simplification, the firm does not consider a “now entry and later reexit” but only an “entry and stay forever” strategy. Furthermore, we do not consider the effects of the value of the option of waiting created by uncertainty.21
In a situation with uncertainty the consideration of an option value of waiting leads to an amplification of the hysteresis effects (equivalent to an increase in the size of Hj and Fj, that is, raising the entry trigger and lowering the exit trigger, and thus widening the band of inaction). See Belke and Göcke (1999) for entry/reexit strategies and for the calculation of the option value effects.
:
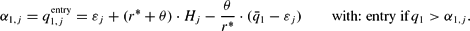
In a situation with static expectations (i.e., with
) or in a long-term equilibrium (with q
) the results reduce to:

If, in the case of an appreciation, a previously active firm j leaves the foreign market it has to pay sunk exit costs Fj. However, the firm will stay active as long as an exit is more expensive than the negative present value of continued activity
. Thus, the exit trigger is given by the condition
. (A later reentry is not considered.)
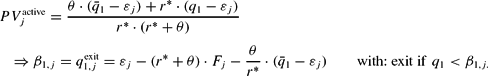
In a situation with static expectations (θ=0) or in a long-run equilibrium (
), we get:
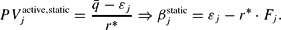
Summarizing, if subsequent to a shock and to an overshooting exchange rate an adjustment process toward the (new) long-run equilibrium is expected, the entry and exit trigger exchange rates are:
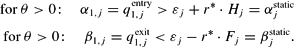
That is, as compared to static expectations, the entry trigger is higher and the exit trigger is lower if the firm expects the exchange rate to be only transitory on an extreme overshooting level.
However, up to now we have not explicitly taken into consideration the coercitive effect of a temporary overshooting on the long-term equilibrium. A temporary depreciation (
) eventually results in a long-term appreciation (
). As is obvious from (
), the reduction of the long-run equilibrium exchange rate
leads to a further increase of the entry trigger α1,j. In the opposite case of a temporary appreciation (
), a long-run coercitive depreciation results (
). Thus, from (
), a negative effect on the exit trigger β1,j follows.
Summarizing all effects on the trigger levels, the band of inaction is widened compared to a situation with static expectations. Thus, for θ>0 we expect the same qualitative consequences on the band of inaction as portrayed for the option value of waiting in a situation with stochastically volatile exchange rates. Belke and Göcke (2001, 2005) describe the consequences of the option value of waiting on the aggregation procedure. Compared to a situation with static expectations (i.e., with θ=0), in Figure 3 the αj/βj–points of the firms are projected to the northwest if the firm considers the adjustment process toward the long-run equilibrium (i.e., if θ>0). As a result, the aggregate macro hysteresis loop will exhibit a kind of behaviour similar to (mechanical) “play”: after a change in the direction of the exchange rate path, we will observe only a very weak (or even no) reaction on changes of q—that is, “play” (see the movement from point A′ to K′ in Figure A.1). Only for bigger exchange rate changes22
Remarkably, the macro behavior now (with a “play” area of weak/no reaction) becomes more similar to the micro behavior (“band of inaction” with no reaction) as described by Baldwin and Lyons (1994).

Effects of adaptive expectations on the size of theremanence and of the coercitive force.
In our very stylized macroeconomic model, we explicitly consider the coercitive effect on the macro level merely via the parameter χ. Thus, all the aspects addressed in this appendix (e.g., the formulation of expectations and the calculation of the triggers, the exact distribution of the heterogeneous firms in the α/β-space as well as the microeconomic effects of changes in the expected long-run equilibrium as a result of macroeconomic coercitive effects) are captured in a very implicit/reduced way via the size of χ. Consequently, our model serves as a first step in analysing path dependence in foreign trade and exchange rate interaction, when agents are heterogeneous.
APPENDIX B
Calculation of the Coercitive Force in the Case of Equally Distributed Firms
The relation between the first impact (q1−q0) and the coercitive adjustment (q2−q1) is equivalent to the relation between the distance AB [between the points A and B in Figure 3(b)] and the distance GB on the 45° line:
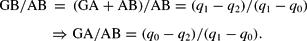
The area of the rectangular triangle AFG equals the area of the triangle FDC of remanent firms, if the triangle GBD and the triangle ABC have the same area. Thus, both hypotenuses (GB and CB) and all catheds (AB and AC of ABC, and DG and DB of GBD) have equal length. Based on the theorem of Pythagoras, the following holds:
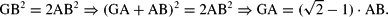
A combination of) and) yields:
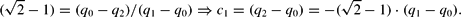
This paper was written when Borgersen visited the University of Münster. The support given to this research by the Norwegian Research Foundation is gratefully acknowledged. The authors thank Eric C. Meyer and Werner Smolny and an anonymous referee for helpful comments. The usual caveats apply.