Published online by Cambridge University Press: 14 July 2005
We study the influence of wage differential on the emergence of endogenous fluctuations. In this way, we introduce a dual labor market, based on the Shapiro–Stiglitz efficiency wage theory in an overlapping generations model. We show that wage inequality is a source of endogenous fluctuations. Indeed, a sufficiently strong wage differential leads to the occurrence of cycles of period 2 and local indeterminacy. Moreover, in contrast to several existing contributions, these results depend neither on increasing returns to scale nor on the degree of capital–labor substitution.
In this paper, we focus on the role of labor market imperfections in the emergence of endogenous fluctuations. More precisely, we analyze the effect of a wage inequality on local stability of the steady state and occurrence of bifurcations.
For the past 20 years, a lot of economists have been interested in the emergence of endogenous fluctuations in macroeconomic models.1
However, most of these authors consider the labor market as perfectly competitive [see, e.g., Benhabib and Nishimura (1985, 1998), Grandmont (1985), Reichlin (1986), Grandmont et al. (1998)]. Recently, in some articles, imperfections in labor market have been introduced. For example, Jacobsen (2000) considers a monetary economy characterized by monopolistic competition on goods and labor markets. In that model, cycles of period 2 can emerge in an economy where involuntary unemployment takes place. Coimbra et al. (2005) introduce unions in an overlapping generations model. In an efficient bargaining framework, these authors conclude that the bargaining power of unions influences the local indeterminacy and occurrence of endogenous cycles.2See also Lloyd-Braga and Modesto (2003) who introduce unions in a model à la Woodford (1986).
Nevertheless, in this field of research, the literature has ignored an important stylized fact of the labor market, namely, the existence of wage differentials. Indeed, empirical studies by Dickens and Katz (1987), Krueger and Summers (1987), Katz and Summers (1989), Gibbons and Katz (1992), and Abowd Kra et al. (1994) highlight the existence and the persistence of wage inequalities in most industrialized countries. A lot of factors can explain these wage differentials, such as the size of the firms, the gender, or the union rate. However, most of these empirical studies show that the existence of wage gaps between employees results from differences in individuals' characteristics, notably skill. Thus, it seems to be important to take into account a wage inequality, based on skilled heterogeneity, in a macroeconomic dynamic perspective. New labor market approaches allow us to explain this wage differential theoretically. In particular, the dual labor market approach, based on the efficiency wage theory developed by Shapiro and Stiglitz (1984), provides an explanation to the rational existence of wage inequalities [Bulow and Summers (1986), Jones (1987a,b), Saint-Paul (1996), or Agenor and Aizenman (1997)].3
See Yellen (1984), Akerlof and Yellen (1986), or Weiss (1991) for a survey on the efficiency wage theory.
The aim of this paper is not to provide an explanation of the existence of dual labor market [Rebitzer and Taylor (1991), Saint-Paul (1991, 1996), Albrecht and Vroman (1992), Teulings (1993)], but rather to show implications of such labor market structure on the dynamic stability. Furthermore, it is important to note that our version of efficiency wage does not correspond to the dynamic approach of Shapiro and Stiglitz (1984). Such a field of research has been explored by Kimball (1994), for instance.
In this way, we consider an overlapping generations model with perfect foresight. The production of a unique final good takes place in two sectors, namely, the primary sector and the secondary sector.5
Contrary to a lot of papers [Benhabib and Nishimura (1985, 1998), Boldrin (1989), Galor (1992), Benhabib and Farmer (1996), Harrison and Weder (2002)], we do not consider a two-sector model with a consumption good and investment good because we essentially focus our attention on the role of labor market imperfections.
As argued by Agenor and Aizenman (1997), this kind of labor segmentation can be interpreted as the coexistence of a services sector assimilated to white collars and an industrial sector assimilated to blue collars.
The dynamics of the model are entirely governed by a two-dimensional system, which directly depends on the wage structure. To analyze this system, we first show the existence and the uniqueness of the steady state. However, the main result concerns the emergence of endogenous fluctuations due to the existence of a wage inequality. Indeed, we show that endogenous fluctuations cannot occur under a weak wage differential. However, when the wage inequality becomes sufficiently high, cycles of period 2 can appear through the occurrence of a flip bifurcation and the steady state is locally indeterminate. Hence, we put in light that wage inequalities are a source of endogenous fluctuations. In other words, when efficiency considerations play an important role in the primary sector, that is, the level of skilled worker effort is relatively high, the nonshirking condition is a source of cycles. Moreover, contrary to a lot of contributions, our results depend neither on increasing returns to scale, nor on the degree of the capital–labor substitution [Reichlin (1986), Woodford (1986), Lloyd-Braga (1995), Cazzavillan et al. (1998), Grandmont et al. (1998), Cazzavillan (2001)]. More generally, this paper shows that labor market imperfections can explain fluctuations due to self-fulfilling expectations and endogenous cycles.
This article is organized as follows: In Section 2, we present the model. In Section 3, we show the existence and uniqueness of the steady state. In Section 4, we analyze the emergence of endogenous fluctuations. Finally, we conclude in Section 5.
In this paper, we consider an overlapping generations model with perfect foresight and discrete time,
. The population is constant and equal to
. Each generation lives two periods. In period t, young consumers born at t and old consumers born at t-1 live together. Households consume at the two periods of their life a unique final good, which is the numeraire. At the first period of his life, each young consumer chooses to supply or not to supply one unit of labor and rents capital to the firms at the real interest rate.
The final good is supplied on a perfectly competitive market. We assume that two types of technology can produce this good. Each type of technology is assimilated to a sector called, primary or secondary sector. Following the dual labor market literature [Doeringer and Piore (1971), Bulow and Summers (1986)], jobs of the primary sector are remunerated at a higher level than in the secondary sector. In this way, we can notably think of a segmented labor market characterized by the coexistence of skilled and unskilled workers who respectively belong to primary and secondary sectors. We can consider that the unskilled workers are more substitutable to the physical capital than skilled workers [Flug and Hercowitz (2000), Koebel et al. (2003)]. Moreover, the secondary sector where the unskilled workers are employed is the most capital intensive. That is why we consider the limit case where capital is only used in the secondary sector. Furthermore, the qualified workers are able to provide a higher level of effort than the unqualified workers.
More precisely, in the first sector, the technology is characterized by constant returns to scale and the firms use a unique input, labor. The firms cannot perfectly observe the skilled worker's effort. To deter the workers from shirking, an efficiency wage of the type in Shapiro and Stiglitz (1984) is set above the competitive one. Therefore, we observe an excess of labor supply in this sector. In the secondary sector, the final good is produced using capital and labor. The production takes place under constant returns to scale. Moreover, we assume that the worker's effort is perfectly observable, and so, the wage is perfectly competitive. Furthermore, each generation is composed of skilled workers (
) and unskilled workers (
), in fixed proportion. The unqualified employees can only work in the secondary sector, whereas the qualified employees who do not find a job in the primary sector can immediately enter the unqualified sector. This last remark is based on the fact that the technology in the primary sector requires a higher level of effort (or qualification) than in the secondary sector. Finally, assuming a perfect mobility of workers between the two sectors, unemployment cannot occur in this economy.
We first present the primary sector. We assume that the production function can be written as follows:

where
denotes the final good product in the primary sector,
the number of skilled workers hired in this sector, and e their level of effort. We suppose in the following that
.
We recall that, in this sector, firms cannot perfectly observe workers' effort. Hence, the employer has to set an efficiency wage so as to deter skilled workers from shirking and incite them to provide a strictly positive level of effort. Assuming that workers' preferences on consumption and effort are separable, the indirect utility function is given by
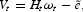
where
denotes the real wage and
the level of effort of the worker, which can be equal to 0 or e1 in the primary sector, and
in the secondary sector. Moreover,
represents the worker indirect utility of consumption per unit of wage; we define it more precisely in the next section. We further suppose that firms consider
as given at period t. The level of effort will be strictly positive (
) if the skilled worker is employed in the primary sector and does not shirk. It will be zero if this worker shirks in the qualified sector and
if he works in the secondary sector. We assume also that the control rate of each worker is constant and noted
. Following Shapiro and Stiglitz (1984), the employer determines the level of wage such that the expected utility of an employee, who produces the effort, is greater than the expected utility of an employee who shirks (nonshirking condition):
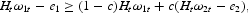
where
denotes the real wage in the primary sector and
the real wage in the secondary sector. The left-hand side in expression (3) measures the expected utility derived by a worker who is not shirking and provides a level of effort equal to e1, while the right-hand side measures the expected utility of a shirking worker as a weighted average of the consumer utility if it is caught shirking and fired (with probability c), and if it is not caught (with probability 1-c). In this last case, the level of effort is zero. We further notice that a shirking skilled worker who is caught immediately enters the secondary sector and provides the same effort as an unskilled worker, e2. At the equilibrium, the employer sets the wage such that the employee will be indifferent between shirking and not shirking.7
In this case, we consider that the employee decides to produce the positive effort e1.
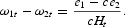
We can note that the nonshirking condition (4) implies the existence of a wage differential, at the equilibrium. This wage inequality increases with respect to the qualification gap between skilled and unskilled workers. Indeed, a greater level of effort in the primary sector constrains the employer to give a higher remuneration in order to deter skilled workers from shirking. We also remark that an increase of the probability of getting caught, c, reduces the wage differential. In other words, employees provide a strictly positive effort for smaller wages in the primary sector, when the probability of detected shirking workers rises. Moreover, we notice that a higher
decreases wage inequality. Indeed, it raises indirect utility per unit of wage, which reduces the incentive for workers to shirk. Then, employers of the primary sector put the wage at a lower level with respect to the competitive wage. Finally, we clarify that, in contrast to Kimball (1994) who is interested in dynamics of the Shapiro and Stiglitz efficiency wage, our nonshirking condition is based on a static version of this last one.
The firms of the primary sector maximize their profits. The first-order condition can be written

In the secondary sector, a continuum of firms of unit mass uses two inputs, the labor
and the capital
in order to produce the final good. Assuming constant returns to scale, the production function can be written
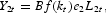
where
is the capital labor ratio in the secondary sector, f the intensive production function and B>0 a scaling parameter. Moreover, we make Assumption 1.
Assumption 1. The intensive production function
is continuous for
for
and p sufficiently high, increasing [
] and strictly concave [
].
At each period, firms maximize their profits. So, we can deduce the usual first-order conditions:
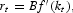
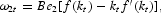
where rt denotes the real interest rate and
the perfectly competitive wage. We represent the dual labor market in Figure 1.

Dual labor market
Before presenting the consumption sector, it is convenient to define the following relationships. First, we note the capital share in the secondary-sector income
. Moreover, we also note
the elasticity of capital–labor substitution. Using (7) and (8),
. Since,
, we can deduce that
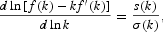
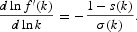
We assume that preferences of a representative household born at
are additively separable between consumption and effort. We further suppose Cobb-Douglas preferences over consumption when young and old, that we, respectively, note
and
. When the individual is young, he supplies one unit of labor. The labor income is spent in final good or saved through the purchase of capital
. The capital fully depreciates after one period of production. When old, individuals rent to firms the capital good at the expected rate
. At the first period, a generation of old lives only one period and has the capital stock as unique endowment. Then, the problem solved by the representative consumer born at
is
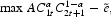
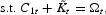
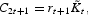
where
is a scaling factor,
,
denotes the level of effort and
is the income of the representative consumer. We derive the following conditions:

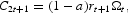
and
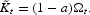
Substituting (14) and (15) into (11), we obtain the indirect utility
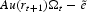
with
. We can note that the relation (17) justifies the indirect utility used in the nonshirking condition (3). Indeed, the real interest rate
is considered as given by the firm at period t and so we identify
to
. Referring to the preceding section, it notably means that a higher
, which corresponds to a higher
, leads to a weaker wage inequality.
To determine the intertemporal equilibrium, we begin by given the expression of the global labor income. Since workers' mobility is perfect (
), we have
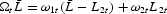
At the equilibrium,
is predetermined by the savings of the previous young generation. Then, substituting (5), (7), (8), and (18) into (4) and (16), we obtain:
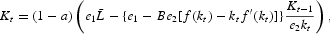
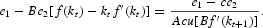
DEFINITION 1. An intertemporal equilibrium with perfect foresight is a sequence
, such that (19) and (20) are satisfied.
The two equations (19) and (20) govern the dynamics of the economy. Indeed, they determine a two-dimensional dynamic system with one predetermined variable, the capital. Moreover, we can remark that these two relations directly depend on the wage and employment structure. More precisely, savings [equation (19)] is defined by earnings of skilled and unskilled workers and and size of the two sectors. Equation (20) corresponds to the nonshirking condition, which shows the extent of the wage gap. We notice that this wage inequality does not only depend on skill heterogeneity, but also negatively on the future interest rate.
In this section, we study the existence and uniqueness of the stationary state of the dynamical system (19) and (20). Our analysis will closely follow Cazzavillan et al. (1998) and Aloi et al. (2000).
A steady state
is a solution satisfying
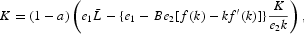
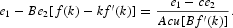
Existence is established by scaling the two parameters A and B in order to normalize the steady-state values of capital and capital labor ratio. In what follows, we ensure the existence of a steady-state, namely with
and
by choosing appropriate values of the scaling parameters
and
such that
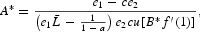
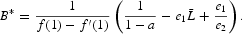
Considering
and under Assumption 1, e1 has to be included in
to ensure that
and
are strictly positive, where
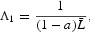

Furthermore, it is obvious to remark that the steady state is unique. Indeed, the left-hand side of (22) is decreasing with respect to k, while the right-hand side is increasing with respect to k. We deduce the uniqueness of K from (21).
PROPOSITION 1. Assuming
, let
where
and
are the solutions of (25) and (26). Under Assumption 1, if A and B are defined by the relations (23) and (24), then
is the unique stationary solution of the dynamic system (19) and (20).
We can remark that the condition
means that the efficiency wage in the primary sector is always greater than competitive wage of the secondary sector, that is,
. In other words, we ensure that the level of effort in the primary sector is such that the nonshirking condition is always relevant. Furthermore, the inequality
implies that the secondary-sector wage is strictly positive.
In this section, we analyze the role of wage differential on the emergence of local endogenous fluctuations. In particular, we show that endogenous fluctuations can occur only if the wage differential is sufficiently strong. In this way, we study the local indeterminacy of the steady state and the occurrence of local bifurcations. So, we first differentiate the dynamic system (19) and (20) in the neighborhood of the steady state
. Indeed, from the Hartman–Grobman Theorem,8
This theorem can be applied if the Jacobian matrix evaluated at the steady state is invertible and if it has no eigenvalue of modulus 1.
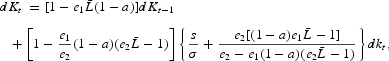
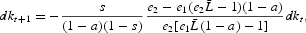
where
and
.
At this stage, we can remark that the wage differential is an increasing function of the parameter e1 at the steady state. Indeed, we have
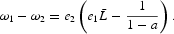
Moreover, when e1 tends to
,
tends to
, and the wage inequality becomes weak. On the contrary, when e1 tends to
,
tends to 0, and the wage inequality is the highest. Most of these remarks allow us to study the influence of the wage differential on the occurrence of endogenous fluctuations.
PROPOSITION 2. Let
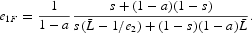
Assuming
, when the wage inequality is small
, the steady state is a saddle. When the wage differential raises, a flip bifurcation occurs
and the steady state becomes a sink when the wage inequality is sufficiently high
.
Proof. From the relations (27) and (28), we can easily compute the two eigenvalues of the Jacobian matrix:
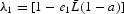
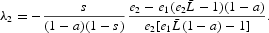
Since
,
. We can notice that
. Furthermore,
is strictly increasing with respect to e1 and varies from
to 0 when e1 increases from
to
. So, there is a unique value
such that
, with
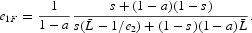
We can conclude that when
, the steady state is a saddle, a flip bifurcation occurs when
, and the steady state becomes a sink for
.
We can first note that a weak wage inequality (
tends to
) implies that the steady state is a saddle. Then, endogenous fluctuations cannot emerge in the model. However, when the wage differential increases, a cycle of period 2 appears through the occurrence of a flip bifurcation. Moreover, the steady-state equilibrium is locally indeterminate when the wage inequality is sufficiently high.9
We recall that the steady state is locally indeterminate if it is locally stable (sink) because the capital is predetermined.
Before explaining these economic features, we recall that the extent of the wage differential depends on the skill gap between qualified and unqualified workers and on the incentives to deter skilled workers from shirking. Furthermore, in our dynamic framework, this wage inequality is also negatively correlated to the level of future interest rate. Indeed, a higher level of the interest rate raises the indirect utility of a worker employed in the primary sector more than if it is hired in the secondary sector. So, it reduces the worker incentive to shirk. In other words, a higher interest rate increases the cost of being fired in the primary sector. Then, the skilled worker will not shirk for a weaker wage differential.
We can now give a more intuitive explanation of the emergence of endogenous fluctuations in this model. In what follows, we first present why a sufficiently high wage differential promotes the occurrence of indeterminacy and endogenous cycles. Then, we highlight the dynamics around the cycle.
To show what the main mechanism is that generates indeterminacy and endogenous cycles, we can rewrite the dynamic system (19) and (20) as
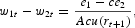
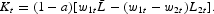
We can easily remark that capital accumulation is strongly correlated to the wage structure. More precisely, in the case of a small wage inequality, due for instance to a small skill gap, the second term in the brackets in equation (34) becomes arbitrarily small. So, capital accumulation mainly depends on a constant term
. On the contrary, when the wage differential is relatively high, it strongly affects the aggregate savings
. Since wage inequality is decreasing with respect to expected interest rate [equation (33)], a variation of this interest rate, yielding a modification of wage differential, implies a large variability of capital accumulation only when the wage inequality is strong enough.
Taking into account that wage inequality is sufficiently high to generate an endogenous cycle, we now give a more detailed explanation of the evolution of the variables around the cycle. To do that, consider that one deviates from the steady state following an increase of the future expected interest rate. Through the nonshirking condition (33), wage inequality is weaker. Since the efficiency wage is constant, it means that the competitive wage becomes higher and then labor in the secondary sector decreases. From equation (34), this leads to a greater level of capital. So, future interest rate increases, and expectations are self-fulfilling, only if the labor in the secondary sector rises in the next period (
). This more important size of the secondary sector reduces the competitive wage in this sector, and raises the wage inequality at the next period. These last effects negatively influence savings and then capital accumulation at the following period (
). These elements clearly explain what happens around a cycle.
It is important to notice that our results do not require increasing returns to scale and the existence of externalities as has often been shown by a large literature [Benhabib and Farmer (1994), Lloyd-Braga (1995), Cazzavillan et al. (1998), or Cazzavillan (2001)]. Furthermore, we can notice that the conditions for the emergence of endogenous fluctuations do not depend on the elasticity of capital–labor substitution. So, contrary to a lot of existing contributions [Reichlin (1986), Woodford (1986), Grandmont et al. (1998)], local indeterminacy and deterministic cycles can appear for all values of this elasticity. Finally, using equation (32), we can easily see that
is an increasing function of s. Hence, a smaller capital share in the secondary-sector income promotes the occurrence of local indeterminacy.
In this paper, we consider a dual labor market, based on the Shapiro and Stiglitz (1984) efficiency wage, in an overlapping generations model. The introduction of such labor market imperfection leads to a wage differential at the equilibrium. In this framework, we show that a sufficiently strong wage inequality promotes the emergence of endogenous fluctuations. Moreover, our results depend neither on increasing returns to scale, nor on the degree of capital–labor substitution. So, this article shows more generally that the introduction of new labor market approaches plays an important role in the emergence of endogenous fluctuations. Future research has to take into account other labor market specifications (unions, matching, etc.) in order to study their influence on the occurrence of endogenous fluctuations.
We thank Rodolphe Dos Santos Ferreira, Teresa Lloyd-Braga, Alain Venditti, an associate editor, and two anonymous referees for helpful suggestions. We also benefited from the comments of participants to the 5th International Conference on Macroeconomic Analysis and International Finance in Crete, May 2001; Fourth International Summer School in Economics in Rome, June 2001; and Conference Theories and Methods in Macroeconomics in Evry, June 2002.
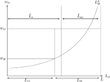
Dual labor market