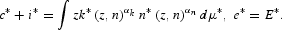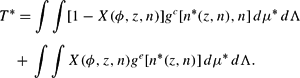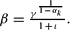INTRODUCTION
An extensive literature addresses the macroeconomic implications of institutional firing costs, a central feature of employment protection legislation (EPL).1
This paper argues that insights into the effects of EPL can be obtained by considering its effect on establishment closure, or “exit.”Exit is an event that leads to potentially large and costly dismissals. Hence, dismissal costs discourage exit as well as firing, which may affect the distribution of establishment characteristics. This creates a new channel through which EPL might have aggregate implications.
Moreover, depending on the regulatory and judicial environment, exit may in fact constitute a way of avoiding dismissal costs. A well-known theoretical result is that EPL should have no effect on allocations in a world of complete markets, and Lazear (1990) conjectures that exit could be one point at which this incompleteness arises. Exit is an important factor of job destruction around the world: consequently, these observations may be of quantitative importance.2
In the United States, Davis and Haltiwanger (1992) find that exit accounts for 12% of quarterly job destruction, rising to 23% and 57% for annual and quinquennial data, respectively. The OECD (1996) reports that, in some countries, over half of annual job destruction is a result of establishment closures.
The paper has two aims. First, it examines the relationship between exit and EPL, and argues that, empirically, exit indeed does appear to offer relief from institutional firing costs. Second, to address the macroeconomic implications of this finding, it develops a general equilibrium model in which the decision to open and close establishments is endogenous. The model nests alternative formulations of exit as special cases, and chooses among them via calibration to measured hazard rates over the lifecycle.
There are four main results. First, the effects of dismissal costs are sensitive to the endogeneity of the exit decision. In an economy with heterogeneous plants, EPL affects aggregates through two channels:
- Reallocation: by changing their hiring and firing decisions, EPL redistributes resources across plants.
- Composition: by affecting their continuation and exit decisions, EPL may affect the degree of heterogeneity across plants. For example, when EPL makes exit costly, unproductive plants may remain in operation when they would not have done so otherwise.
The quantitative importance of the compositional effect is an issue that only can be addressed in a model in which, as here, the exit margin is endogenous and carefully calibrated. I show that this effect significantly increases the magnitude of the impact of EPL on aggregates.
Second, the effects of dismissal costs are highly sensitive to the extent to which closing establishments in particular are obliged to pay them. When closure annuls benefits commitments, the compositional effect is eliminated, so that aggregate employment is suppressed by much less than otherwise. Although this is to be expected, what is surprising is that the effect of EPL on employment weakens by over a third, even though exit accounts for little over one-tenth of job destruction in the data.
Third, the model has implications for the relationship between EPL and the structure of job turnover that are consistent with the data. Based on a detailed comparison of labor markets in the United States and Portugal, Blanchard and Portugal (2001) argue that high dismissal costs appear associated with lower job turnover rates, and also with a higher proportion of job turnover attributable to entry and exit. When dismissal costs are lifted on exit, the model turns out to provide a simple account of these phenomena. When dismissal costs are high, exit becomes a “cheap” method of job destruction. Because the youngest plants are the ones that are at most risk of closure, this disproportionately favors them.
Finally, theory suggests that any real effects of EPL are indicative of some degree of contract incompleteness in labor markets. The results of the paper turn out to be informative as to the stage of the lifecycle at which contract incompleteness is likely to operate.
Section 2 provides an overview of the treatment of dismissal costs on exit around the world, and discusses some implications. Section 3 outlines the structure of the model. Section 4 defines the equilibrium concept for the economy, and outlines the calibration procedure. Section 5 introduces dismissal costs into the model, and Section 6 presents results on the influence of the exit margin and discusses the results.
AN OVERVIEW OF WORKER ENTITLEMENTS ON EXIT
Employment Protection
EPL is often modeled as a cost to firing. As a result, mandated severance payments have received the most attention among the different forms of EPL. They involve direct costs to job destruction, are simple to quantify, and are found by Lazear (1990) to be negatively related to employment aggregates. EPL may have other components such as advance notice requirements or the provision of a detailed justification to regulators. However, under simple assumptions, many EPL policies are equivalent to a dismissal cost.3
For example, if a firm finds it better to fire workers than to employ and pay them, a severance payment of τ quarters' wages is equivalent to having to notify them τ′>τ quarters in advance of a firing, where τ′ takes account of the fact that the marginal revenue product of the workers will be below their wage (otherwise it would not have been optimal to fire them).
See Addison and Teixeira (2003) for a survey.
What is the relationship between EPL and job flows? Blanchard and Portugal (2001) provide a detailed comparison of the labor market structure and institutions of the United States and Portugal, with an eye toward developing internationally comparable data. They find that, compared to the United States, job flows in Portugal are smaller, and argue that differences in EPL regimes can account for this difference. Table 1 reports the correlations between different measures of EPL and the magnitude of job flows: most of the correlations are indeed negative.5
The severance pay measure AT is from Addison and Teixeira (2003), whereas NICO is from Nicoletti et al. (2000). The remaining measures are broader indices of EPL, and are drawn from Mercer Human Resource Consulting (2003), Heckman and Pagés (2000), Nickell (1997), OECD (1999), Di Tella and MacCulloch (1999), and Botero et al. (2003). “WCR” = World Competitiveness Report. Labor market data is from the OECD (1999).

Blanchard and Portugal (2001) also observe that, in Portugal, entry and exit are more important as factors in job turnover than in the United States. They do not develop an account for this phenomenon, however, and it is less transparent how dismissal costs alone might be related to these findings.6
Although the contribution of entry and exit to job flows is also reported for multiple countries in OECD (1999), the authors note that their data set is likely to misidentify many entries and exits and, moreover, that, in this regard, it is not internationally comparable.
This section provides a discussion of how the treatment of dismissal costs may depend on whether firings are taking place at a continuing establishment or at one that is closing: something that all of these measures neglect. Let θ∈[0, 1] be the expected proportion of regular severance pay that impacts firms on exit: I argue that the empirically relevant values of θ are less than one. There are two reasons why this might be the case. First, the regulatory regime may grant exemptions for plant closures. Second, there may be no funds available at the firm to cover such payments.
Exemptions
Severance pay—mandated or otherwise—only constitutes a firing cost in the event that it is employer-funded at the time of dismissal. In some countries, there exist government-sponsored insurance funds that cover severance pay resulting from plant closure. In several others, there is discretionary government support.7
In the event of such payouts, the corresponding funds are drawn from the broad tax base: severance payments will not impose firing costs on the establishment, and as a result they will not affect incentives to hire and fire at any point over the lifecycle. There may be a proportion 1−θ of these funds that are covered, or an ex-ante probability 1−θ≤1 that payments from this fund are approved. Alternatively, in countries in which union presence is strong, this may be the object of negotiation: for instance, Dutch employment law requires that employers consult with unions regarding the arrangement of severance payment in case of “collective dismissals,” except in case of bankruptcy (see later). Then, in expectation, θ represents the proportion of severance pay that is assessed on the owners of closing plants.Insolvency
So far, we have assumed that a firm that closes a plant is in fact able to fulfill its financial obligations. However, this may not be the case: plants that close may often do so under conditions of insolvency.8
A point to keep in mind is that insolvency does not necessarily imply exit either. In many countries, the explicit purpose of bankruptcy law is to provide for the financial reorganization of a firm so that its plant or plants may continue in operation—see Korobkin (1996). The presumption is that a firm may find itself in financial problems that are not connected to the long-term viability of the establishment. Hence, in what follows, I discuss the case of a firm that has chosen to close an unviable plant and that in addition is insolvent.
In the event of insolvency, there are insufficient funds available at the firm to cover all its outstanding financial claims. Because the owners are residual claimants, their continuation payoff from the firm is zero, and it is the remaining creditors—potentially including workers—who are left to fight over any remaining funds. In a few countries (Austria, Italy, South Korea, and Venezuela), severance payments are secured claims in that companies must maintain book reserves to cover a portion thereof. Thus, in these countries a portion of severance payments might be disbursed even if the company is insolvent and liquidated. However, the owners receive no further income from the firm regardless: again, formal firing costs do not necessarily function as such on exit, so that the de facto value of θ is zero.
In practice, this is complicated by the fact that, although owners are residual claimants, judges have discretion in setting the relative priority of claims, and do not always strictly follow the order set down in the law. For example, Franks and Torous (1989) find that it is not uncommon for equity holders to receive priority above debt holders in liquidation proceedings in the United States, even though legally the opposite should occur. Similarly, Johnson (2003) finds that in China, although severance pay and other employee claims have first priority in liquidation proceedings, the legal order is often not followed. Hence, there may be some positive value to equity at an insolvent firm—although it is likely to be low. In principle, this value may then depend on the priority of the claims of equity in liquidation proceedings relative to those of other claimants. In particular, whether or not severance pay affects their profits at this point—and, hence, their hiring and firing earlier on—will depend on whether or not employees have priority over owners.
In the legal treatment of employee claims, many countries distinguish between different kinds of worker claims, generally between claims based on labor services that have already been delivered (e.g., unpaid wages), on the one hand, and benefits, on the other. Most countries consider back wages as preferential claims, often dealt with before other private claims. However, there is much more variation regarding the treatment of benefits such as severance pay—indeed, worker benefits are not even mentioned in the bankruptcy statutes of some countries.
In countries where worker benefits claims are treated with high priority, they will be paid. For example, in Denmark, France, and the Netherlands, the proceeds of liquidation are used first to pay for the administration of those funds, and then to cover all employee claims before bond holders' claims beyond earmarked book reserves are dealt with.9
See Johnson (2003) for a survey.
Where benefits claims are treated with low priority, they are more likely to go unpaid. In the United States, for example, employee wage claims are in the third category (out of five) of unsecured claims, behind creditors' claims for unmatured interest and some equity holders: benefits claims are in the fourth category. In the United Kingdom, to the author's knowledge, insolvency law makes no mention of employee benefit claims at all. In the extreme case of South Africa, employee contracts become void on the declaration of insolvency, so that not even back wages need be honored.10
Based on this discussion, what is a reasonable value of θ? First, assuming that θ may vary across countries, what is most relevant is its magnitude in countries where EPL is strict. For instance, consider Portugal and Spain, both among the countries with the most extensive EPL regimes. In both, large dismissals are often covered by wage guarantee funds, the explicit role of which is to finance severance pay at insolvent firms. Second, mandated benefits will not affect employer hiring behavior to the extent that these claims are placed under conditions of insolvency.11
This applies directly to single-unit plants: multi-unit plants may find themselves having to pay firing costs when they close plants. However, in the United States, Kim (1998) reports that only 20% of plants are owned by multi-unit firms. Moreover, if θ is related to the ownership structure then it may be negatively related to dismissal costs, since the choice of ownership structure is presumably endogenous to some extent. For instance, high dismissal costs might increase the cost of operating multi-unit firms as compared to single unit firms for whom, on exit, dismissal costs would be unenforcible. Alternatively, complicated holding patterns might achieve the same goal.
Further Implications: Exit, EPL, and Other Benefits
The remainder of the paper examines the aggregate effects of variation in the treatment of firing costs on exit. This inquiry will underline whether the considerations raised herein could have quantitatively important effects. Before doing so, however, it is worth noting that the treatment on exit of employee benefits more broadly also may be important, even in countries where mandated severance pay is low. First, if voluntary severance pay forms part of an optimal labor contract, then whether or not they are paid will depend on whether or not there is a guarantee fund, on bankruptcy provisions, and so on as discussed earlier. Second, even if severance payments are not present, the structure of bankruptcy priorities may still have an effect on job destruction. The reason for this is that, if employee claims have low priority, declaring bankruptcy may be a way to avoid the payment of back wages, as well as other benefits. One can think of the avoidance of back wages as a negative dismissal cost, or more generally as a lowering of dismissal costs on exit. As a result, the priority of worker claims in general may matter for job flows, and not simply the priority (or the existence of) mandated severance or other benefits. Although there is much empirical evidence suggesting that dismissal costs have negative effects on various labor market aggregates, surveys of the related literature have not entirely coincided in their conclusions.12
See, for instance, OECD (1999), Heckman and Pagés (2000), Addison and Teixeira (2003), and Cahuc and Zybelberg (2004).
More broadly, the literature on bankruptcy has concentrated on the treatment of debt holders versus shareholders,13
neglecting the treatment of employees as claimants in bankruptcy or liquidation proceedings. In most countries, it is routine to award back wages first priority (along with government tax claims). Employees, however, often have claims beyond back wages—severance and pension claims—that require satisfaction. These claims imply that employees can be thought of as long-term bond holders,14 even though their claims do not have the same priority as those of formal creditors and although—unlike the assets of formal creditors—these claims are highly illiquid. Thus, although this paper does not pursue the topic further, worker benefits may constitute a potentially interesting nexus between corporate governance and labor market regulation that, to this author's knowledge, has not been addressed in the literature and that may have important theoretical as well as welfare implications.MODEL ECONOMY
In sum, these considerations and the prevalence of exit as a factor of job destruction suggest that the treatment of dismissal costs on exit may have quantitatively important effects on labor market performance. This section develops a general equilibrium model to study these implications within an otherwise standard macroeconomic framework for labor market policy analysis.
There are two major frameworks that have been used to study the effects of firing costs: that of Hopenhayn and Rogerson (1993) (henceforth HR) and that of Mortensen and Pissarides (1994) (MP). I work within the HR framework, as it is the most natural of the two in which to address the link between firing costs and exit.
The reasons are as follows. First, differentiating between job turnover and establishment turnover is central to the issue at hand. The MP framework does not distinguish between entry and hiring, nor between exit and firing: in contrast, the HR framework is built around the industry entry and exit model of Hopenhayn (1992), which is designed to pay close attention to these distinctions.15
Although the model of Fonseca et al. (2001) can be interpreted as extending the MP model to conceptually distinguish entry from hiring, there is neither entry nor exit in equilibrium, so it does not constitute a suitable framework for the current inquiry.
There are two salient differences between the HR and MP frameworks that are relevant for the study of EPL. First, calibrated versions of the former generally imply that EPL decreases aggregate employment, whereas the MP model can imply the opposite—although neither model has an analytical prediction either way.16
See Ljungqvist and Sargent (2000), and Appendix B in the current paper.
For example, Samaniego (2001) shows that, in the presence of shocks to the rate of technical change, the HR framework can account for the 1970s decrease in employment in Europe.
For these reasons, the HR model is the most natural of the two frameworks in which to begin an inquiry into the influence of entry and exit on job flows, allowing me to address the question at hand within an otherwise standard labor market policy model. Although it is beyond the scope of the paper, it would be interesting to extend the MP framework to shed further light on the question at hand.
The main innovation of the model is the approach to exit. Exit is state-dependent, and determined on the basis of stochastic fixed costs. A similar approach has been used to endogenize other aspects of establishment dynamics in a macroeconomic framework—for example, the price adjustment model of Dotsey et al. (1999) or the “lumpy investment” models of Cooper et al. (1999) and Thomas (2002).
Establishments
Output
There is a continuum of plants of endogenous mass that operate in discrete time. At any date t a plant is characterized by an idiosyncratic productivity shock
, its capital input kt and its labor input nt. It uses these to produce output of a numeraire good yt, according to the production function

where γ is an exogenous productivity growth factor and αk + αn < 1. Idiosyncratic shocks follow a Markov process defined by a cumulative distribution function F(.|zt). Output may be used for either investment or consumption.
Let wt be the wage rate for labor and rt the rental rate of capital. There is also a tax that must be paid whenever employment is reduced. For continuing plants, this cost is gc(nt, nt−1). If a plant is firing workers because it has chosen to exit, however, the cost is ge(nt−1)≤gc(0, nt−1). The proceeds from taxation are redistributed to households via a lump-sum transfer18
An alternative is to redistribute the firing cost directly to the fired worker. However, it does not affect the aggregate behavior of the model. See Appendix B.1
Entry and exit
Aside from the numeraire, there is an intermediate or “managerial” good, one unit of which may be used to create a new establishment. They are born with nt−1=0, and their initial productivity shock is drawn from a distribution ψ(z). Let pt be the price of the managerial good. In equilibrium, pt will equal the price of a new establishment.
Independently of the idiosyncratic productivity process, establishments also are subject to “continuation shocks,” drawn from a set Φ⊂R+. At the beginning of period t, before the realization of zt, an establishment draws a value ϕt∈Φ, and must pay ϕt in units of the intermediate good in order to continue in operation. Establishments whose continuation values are below ϕtpt in expectation will optimally choose to exit. There is a cumulative distribution function Λ over Φ, and draws are independently distributed across establishments and over time.
The model of exit is one of state-dependence, based on stochastic fixed costs of operation. This allows for probabilistic exit that, along with the stochastic process underlying productivity, will capture the gently decreasing exit rates over the lifecycle that have been found in the data, as well as the fact that observationally equivalent plants may display divergent continuation behavior. This is distinct from related models, where exit is exogenous, or else is certain depending on whether productivity is above or below a particular threshold—a bifurcation that implies excessively uneven exit rates over the lifecycle.
Establishment value function
As this discussion suggests, any given establishment is characterized by its idiosyncratic shock zt and its level of employment in the previous period nt−1. Define
to be the space of possible pairs (zt, nt−1). The aggregate state variable of the economy will be xt≡{Kt, μt}, where Kt is the aggregate capital stock and
denotes the measure over individual establishment states. Let Γ be the law of motion for xt, so that xt+1=Γ(xt). The functional Γ will be determined in equilibrium by the plants' optimal employment and entry/exit decisions, as well as the shock process F.
As specified, the economy is nonstationary because of the presence of exogenous growth. However, the procedure of King et al. (2002) implies that it exhibits a balanced growth path, which allows the application of standard recursive solution methods. The paper will focus on such a path, in which there exist values of entry and labor inputs that remain constant, whereas prices wt, pt, and output increase by a factor
each period. Along this path, although aggregates are stationary, individual plants may be subject to quite complex lifecycle dynamics, and there will be significant reallocation of resources among plants.19
Although growth is not the focus of the paper, the calibration procedure of Kydland and Prescott (1982) is most appropriate for growth models, as stylized facts from the growth literature are used to pin down various parameters such as the discount factor and the form of the utility function—see Cooley and Prescott (1995). Consequently, although it complicates the presentation somewhat, this feature is consistent with the methodology of calibration.
As noted, continuation costs are paid in terms of the managerial good. This is for two main reasons. First, it ensures that payments increase geometrically along a balanced growth path. Other models either impose exogenous exit, or imply that costs such as ϕ increase exogenously. The former does not account adequately for differential hazard rates among cohorts, whereas the latter lacks an economic foundation. Second, firing costs typically lower profits, and this is one reason why labor demand decreases in the HR framework. Here, the value of entry pt equals the price of the managerial good, which is also tied to the costs of continuation. This would be expected to weaken the aggregate impact of firing costs. As noted, the HR framework diverges from the MP framework in its predictions for the effect of EPL on employment, so this is a feature that on its own should move in the direction of reconciliation.
For brevity, the dependence of variables upon the state xt is suppressed. Let ι be the interest rate. The establishment value function V is, then,

where C(zt, nt) is the expected continuation value of the firm, given by
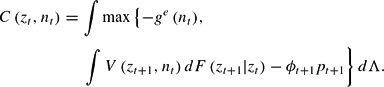
Simply put, each period the plant chooses its inputs, and makes a decision as to whether or not to close down based on whether the expected net benefit of continuation ∫V(zt+1, nt) dF(zt+1|zt)−ϕt+1pt+1 exceeds the cost of exit −ge(nt). If the continuation cost ϕt+1 is sufficiently large, it will prefer to exit.
Some comments on the solution to this problem are in order. First, given the choice of labor nt, the optimal choice of capital input k* is a static decision and is easily derived:

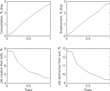
However, the presence of firing costs implies that the problem is not differentiable in nt, so the optimal choice of labor input n* cannot be characterized analytically. In general, for any given nt−1, if zt is sufficiently high then the optimal labor input n*(zt, nt−1)>nt−1 whereas, if zt is low, then some firing occurs and n*(zt, nt−1)<nt−1. However, as long as there are firing costs, there is also an intermediate range of zt such that n*(zt, nt−1)=nt−1. In this range, employment is kept constant so as to avoid the firing cost. See Figure 2 for an illustration.

Timing of events in the model.

Optimal employment rule n*(zt, nt−1), in the presence of firing costs, by plant type.
As a result, some plants may be larger than they would in the absence of firing costs, whereas others may be smaller. Consequently, whether or not firing costs increase or decrease aggregate employment depends on the distribution of plant types, as well as on general equilibrium effects that this distribution may have on the wage.
Finally, let Et be the mass of entrants in period t, and let X be the establishment's optimal probability of exit.20
Generically, X will be single-valued as it is defined after the revelation of the continuation cost ϕ. In cases of indifference, a tie-breaking rule can be assumed that will not matter for aggregate behavior as such cases will be of measure zero. It is given by:

where nt=n*(zt, nt−1).

Although complicated, this condition simply states that the measure over types in any given period is determined by the employment decisions and idiosyncratic shocks of plants that survive the previous period, plus any new entrants.
Households
There is a [0, 1] continuum of infinitely lived households. Households are involved in several activities. They supply time in the form of labor to a competitive market. They also spend time creating the intermediate or managerial good: it, too, trades on a competitive market. If a household spends mt hours producing the managerial good, the resulting output is given by a production function

Finally, using the income they derive from these activities and from assets (plants) they already own, they purchase new assets, consumption, and investment goods.
Preferences over streams of consumption
and leisure
take the standard form

A household's maximization problem may be specified recursively using the following value function:
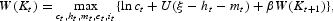
subject to its budget and capital constraints:
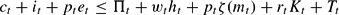
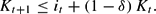
Here ct= consumption; it= investment; Kt= household capital; mt= hours spent creating the managerial good; ht= hours spent working; Πt= income from currently owned plants; et= purchases of new equity (new plants); and Tt= transfers.
The household problem is entirely standard, except for the multiple uses of time. The first-order condition for time use will be that households are indifferent between alternate activities. This pins down mt in equilibrium, playing the role usually played by a free entry condition:
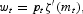
where pt, the price of the managerial good, equals the value of opening a new establishment:
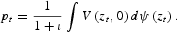
Managerial market clearing requires that output of the managerial good equals the total number of new entrants plus any continuation costs that are paid. If X is the optimal exit rule, the corresponding condition is
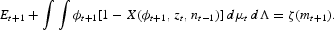
EQUILIBRIUM
This section describes the conditions that characterize equilibrium, as well as the algorithm for solving the model. In a nutshell, the framework is a general equilibrium model with neoclassical firms and households, in which entry and exit are endogenous and in which labor may be used in entrepreneurship as well as in production. The equilibrium conditions will simply be that, taking prices as given, all agents make these decisions optimally, and that markets clear.
DEFINITION. A stationary equilibrium is a value function V*, an exit rule X*, employment and capital rental rules n* and k*, entry E*, transfers T*, household decision rules regarding consumption c*, time use h* and m* and equity purchases e*, prices p*, w* and r*, an aggregate state x*=(K*, μ*) and a law of motion for the state Γ that satisfy:
- Stationarity: Et=E*, Tt=T*, ct=c*, et=e*, Kt=K*, ht=h*, mt=m*, pt=p*, wt=w*, rt=r*, xt= x* and x*=Γ(x*), where Γ satisfies equations (3) and (6).
- Optimality: the decision rules solve the establishment problem (1) and the household problem (4).
- Optimal time use: equation (7) is satisfied.
- Market clearing: equation (9) is satisfied, and the labor market clears:

- Aggregation:

- Government budget balance:


A way to make these conditions more transparent is to describe the algorithm they generate for computing the equilibrium.
Take a guess for w*. This can be used to compute V*, which yields decision rules as well as a value for entry. The optimal time use equation (7) yields mt, which maps into the supply of the managerial good.
By Lemma 1 in the Appendix, equation (3) has a unique fixed point μ*. μ* can be computed down to a constant that is equal to equilibrium entry E*. The value of E* is determined by equations (7) and (9).
At this point, labor demand and labor supply can be computed by combining the household budget constraint (5) with the aggregation and government budget balance conditions. The wage w* is simply adjusted so as to ensure that the labor market clears.
See Hopenhayn and Rogerson (1993) for a discussion of conditions for equilibrium existence in related models.
Calibration
To calibrate the model, I match a number of statistics on job and plant turnover in the United States. The United States is one of the countries among which institutional firing costs are lowest. I set mandated dismissal costs in the benchmark economy to be zero, so that gc(nt, nt−1)=0, ge(nt)=0.
Broadly, calibration proceeds as follows. The structure of the stochastic productivity process F is related to the extent of job turnover in the economy. By contrast, the entry distribution ψ is related to the relative size of the young compared to the old. Given these two distributions, the factors that govern exit (Φ and Λ) are chosen so as to ensure that hazard rates over the lifecycle match the data, subject to the constraint that plant turnover must account for a reasonable proportion of job turnover.
The following assumptions will aid in this task. Let F* be the stationary distribution of F.
Assumption 1. F(.|zt) is decreasing in zt.
Assumption 2.
for all Z∈[real ].
Dominance Assumptions 1 and 2 endow the lifecycle dynamics in the benchmark economy with the following characteristics, which are proven in Appendix A.
PROPOSITION 1. The probability of exit is decreasing in size.
PROPOSITION 2. The probability of exit decreasing in age.
PROPOSITION 3.Average size is increasing in age.
Assumption 1 implies that firms that are more productive tend to remain so, whereas Assumption 2 implies that plants are generally born small, as the empirical literature finds—see Evans (1987) and Dunne et al. (1989). The evolution of productivity at a plant may thus be interpreted as a stochastic learning process, censored by the exit rule. Propositions 1 and 2 imply that hazard rates in the benchmark economy increase with age and decrease with size, as in the data.
The length of time between periods is chosen to be one quarter. This increases the challenge of distributing endogenous hazard rates across plants of different ages in an empirically reasonable manner. To see this recall that, in the related HR model, most exit occurs within the first period of life.
The main modeling innovation of the paper is the exit structure. I choose Φ={0, ϕ, ∞}. This is the minimal structure that allows plants of all sizes to survive with positive probability, plants of all sizes to exit with positive probability, and larger plants to be more likely to continue—as documented in Dunne et al. (1989). It also nests the exit structures of related papers, so that the calibration process will be informative regarding the most appropriate choice of model. The details of the procedure may be found in Appendix B.
Table 2 displays the steady-state statistics of the model economy. The matches are remarkably good. In particular, exit rates are accurately distributed over the lifecycle. This is the case even though the extent of exit because of shocks that are small enough that at least some establishments would survive them in steady state turns out to be exactly 50%. That the model yields more realistic dynamic behavior at the establishment level, particularly across age groups, supports its empirical relevance. Although not explicitly matched, the age profile of the economy is also close to that found in U.S. data, with about one-third of plants under 6 years of age and another one-third between 6 and 20. This is another reflection of the success of the model in matching hazard rates over the lifecycle, in spite of the challenge posed by the fact that these hazard rates are endogenous and the model is quarterly.21
It is useful to consider that the only difference in terms of parametrization between this and the related HR model is that exit is governed by three parameters rather than one: for example, they share the same parametrization for the productivity shock structure. Thus, the addition of two parameters is shown to be sufficient to match lifecycle dynamics in the data much more closely. See Appendix B. 4 for a discussion.

DISMISSAL COSTS
Henceforth, I set gc(nt, nt−1)=τ×wtmax{0, nt−1 − nt}, so that there is a firing cost equivalent to τ quarters of the equilibrium wage. I also set ge(nt−1)=θ×gc(0, nt−1), so that θ is the fraction of regular dismissal costs that are assessed on exit.
This section studies the effects of introducing dismissal costs into the benchmark model. This will serve to compare the behavior of the current model to that of related models. In what follows, I refer to an economy in which dismissal costs are equivalent to one year's wage payments (τ=4). This is a widely used benchmark in the literature and is regarded as being within empirically relevant bounds.22
For the (mostly OECD) countries they examine, Addison and Teixeira (2003) use the months of salary to which blue-collar workers are entitled as severance pay on dismissal after 10 years of service, finding that this ranges between 0 and 20. They also list other indicators of EPL, finding high rank correlations across different measures.
For purposes of comparison with this literature, for now I set θ=1, so that dismissal costs must be paid regardless of whether or not an establishment is closing. The results of varying θ—the extent to which dismissal costs must be paid on exit—are the focus of the paper and are covered in Section 6 The reader who is most interested in these results may skip the remainder of Section 5
Exit and Dismissal
I begin with an examination of the long-run effects of introducing dismissal costs τ>0 into the benchmark economy. I also take this as an opportunity to compare the behavior of this framework with that of related models, and discuss the model features that appear to be important quantitative determinants of the effects of dismissal costs.
Table 3 reports the changes in employment, consumption, output, and welfare that result from the imposition of dismissal costs worth one year's wages. Table 3 also reports the results of two closely related models, those of Hopenhayn and Rogerson (1993) (HR) and Veracierto (2001).

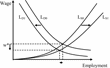
The behavior of the three models is qualitatively similar. Dismissal costs have the effect of suppressing employment, steady-state consumption, and real GDP. The reason for this is as follows. On the one hand, firing costs might be expected to increase employment by decreasing the willingness to reduce plant-level employment after negative shocks. However, the expected cost of firing also acts as a disincentive to hiring. Moreover, caeteris paribus, a rise in the firing cost decreases expected lifetime profits, and decreases total factor productivity because firing costs misallocate labor across plants. The latter effects dominate, and the labor demand schedule shifts to the left.
The decrease in expected lifetime profits also shifts the labor supply schedule to the right, so that the overall effect of firing costs is ambiguous in general equilibrium. However, the labor demand effect dominates in calibrated versions of the model.23
See Appendix B for a discussion.

Equilibrium in the labor market. Firing costs lower equilibrium profits, resulting in a shift in labor demand from LD0 to LD1. Labor supply shifts from LS0 to LS1. The high wage elasticity of labor supply in the calibrated model leads to a decrease in equilibrium employment.
However, quantitatively speaking, the aggregates of the current economy respond to firing costs much more strongly than those of related models. This suggests that endogenizing and calibrating the exit margin can have a significant impact on the aggregate policy response of the model economy.
Aside from the exit margin, there are a few other ways in which the model economy departs from the related literature. In Appendix B, further experiments isolate the endogeneity of exit and period length as the two most important features behind these quantitative differences, and the interested reader may refer to that section for details.
Effects on Job Flows, θ=1
Table 4 investigates in more detail the interaction between plant turnover and firing costs. There are two main results. First, hazard rates decrease–as is to be expected, since firing costs also make exit costly. This effect is not large (a decrease of 4%), but this is enough to significantly affect the composition of the establishment pool: the average value of zt drops by fully 10%.

Aggregate labor input in production equals the expression ∫n*(z, n) dμ*. Thus, there are two channels whereby heterogeneity across establishments might respond to the presence of firing costs:
- Reallocation: Firing costs suppress both hiring and firing, affecting the distribution of labor across plants. This channel involves variation in n*.
- Composition: When exit is endogenous, the presence of firing costs may affect which firms do and do not survive. This channel involves variation in μ*.
In a model in which exit is exogenous, exit would simply operate as another factor leading to apprehension in hiring and to the misallocation of labor. However, when exit is endogenous, plants can avoid firing costs to some extent by not exiting. The resulting change in the distribution of plant types generates a significant drop in average plant productivity. Although exit rates themselves do not change much, there also are more plants in the distribution that are likely to suffer shocks that lead to exit. In the absence of firing costs, these plants would be “weeded out” as soon as they receive a negative continuation shock, whereas here they may instead persist for several periods.
Second, the structure of job flows is little affected by firing costs. The distribution of job turnover across new, continuing, and exiting plants is essentially the same as in the undistorted economy, and the proportion of employment that is created and destroyed each quarter also varies little. The significance of this result will become clear in brief.
EXIT AND DISMISSAL COSTS
Having examined the long-term impact of dismissal costs in the benchmark economy, we turn to the quantitative implications of varying θ, the extent to which dismissal costs must be defrayed by establishments that are closing their doors. Unless otherwise mentioned, what follows continue to assume that τ=4 in the distorted economy.
Job Flows and the Value of θ
Section 2 argued that the empirically relevant values of θ are low. I show now that, in this case, the model behaves very differently from when θ = 1. Moreover, it is capable of replicating the “stylized facts” regarding firing costs and job flows reported in Section 2. To make this point clear, we examine the polar case in which θ=0, so that closing plants are exempt from firing costs.
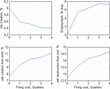
Figure 4 displays the results of varying the dismissal cost τ between 0 and 4. Notably, an increase in dismissal costs is associated with a decrease in the rate of job turnover, as well as an increase in the importance of birth and exit as factors of job turnover. This is in stark contrast to the results when θ=1.

Varying the firing cost τ, while keeping θ =0. Job creation is reported as a proportion of total employment. Because the model is stationary, job creation rates equal job destruction rates.
How do these results compare with the data? Blanchard and Portugal (2001) provide a detailed comparison of job flows in the United States and Portugal, where dismissal costs are much higher. They report that quarterly job turnover in Portugal is 60–70% of that the United States. They also report that the proportion of job destruction because of exit in Portugal is about 50% higher than the corresponding figure for the United States, and that the relative proportion of job creation because of birth is even larger. The latter findings are based on annual series for entry and exit, and such large differences may be sensitive to the extension to higher frequency data.24
For instance, quarterly data would capture some additional short-lived firms that are missing from the annual data and which are probably more common in the United States because of the presence of firing costs, high costs of entry, and other regulations in Portugal.
When θ=1, the behavior of the model is at odds with these findings. As seen in Table 4, the suppression of job turnover as a proportion of employment is weak, and there is essentially no link between plant turnover and job turnover. Hence, when firing costs treat continuing and exiting plants symmetrically, the behavior of the model is not consistent with empirical findings on the structure of job flows. However, when θ=0, the model is consistent on all counts: job turnover is suppressed, and entry and exit increase significantly as factors of job turnover. It is also interesting that the effect of EPL on entry is stronger than that on exit—which also is a feature of the data.
Why is this the case? Recall that there are two channels whereby heterogeneity across establishments might respond to the presence of firing costs: the reallocation and composition effects. Each of these also will be responsive to θ, and each is capable of increasing the importance of exit for job destruction.
- Reallocation effect on n*: Even if exit rates are not affected, firing on exit is cheaper when θ is low. Hence, hiring need not be as restrained as otherwise, and plants that close will be larger as a result.
- Compositional effect on μ*: plants that are considering firing workers may choose to exit, as, when θ is low, this allows them to avoid the firing cost.
When θ=1, the compositional effect was seen to be quite strong in that some low-productivity plants chose to remain in operation to avoid the cost of large firings on exit. However, when θ=0, this effect is eliminated: exit rates do not change compared to the benchmark economy, and neither does average zt. The only remaining channel is that of the reallocation of resources across plants.
Because exit allows for costless firing, hiring should be relatively less apprehensive among groups that face a comparatively high risk of exit—that is, the young. Hence, this also accounts for the fact that hiring at birth becomes more important as a factor of job creation in the presence of EPL.
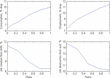
Aggregates and the value of θ
Figure 5 displays the effects of varying θ between zero and one, under constant dismissal costs equivalent to one year's wages (τ=4). When dismissal costs are imposed on exiting plants, employment decreases by 11.2%. When they are not, however, employment decreases by only 7.1%. Similarly, steady state consumption decreases by only 6.4% when θ=0, compared to a decrease of about 10% when θ=1. Moreover, the welfare cost of firing restrictions drops from 2.3% of steady state consumption when θ=1 to 0.6% when θ=0. Although it is to be expected that lowering θ should decrease the influence of EPL upon aggregates, the magnitude of these effects is surprising, as exit accounts for under 15% of job destruction, whereas relieving EPL on exit lowers the effects of EPL by more than twice as much.

Effects of varying firing costs on exit, θ, while keeping firing costs on continuing establishments constant.
Why is this the case? Recall that aggregate labor input in production equals the expression ∫n*(z, n) dμ*. Given changes to the employment rule n* in the face of dismissal costs, the magnitude of this reallocation effect will interact with any compositional changes to μ*. However, in the case that θ is low, this compositional channel was found to shut down, so the firing cost no longer affects the distribution of plant types μ*. Thus, the compositional effect magnifies distortions in the labor market due to changes in n*: consequently, its removal when θ=0 has effects that are much larger than one might expect simply based on the prevalence of exit as a factor of job destruction.
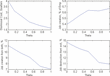
To get another sense of the quantitative importance of θ, Figure 6 examines the extent to which variations in θ could influence the measured employment effects of dismissal costs. To do so, I vary θ, plotting the values of τ that lead to the same change in employment as setting (τ, θ)=(4, 0). To put it another way, I examine the behavior of the economy along the isoquant of policy combinations (τ, θ) such that employment is exactly 7.1% lower than in the benchmark undistorted economy.

Effects of changing τ and θ together to keep the employment effect constant.
The range of dismissal costs that are consistent with the same level of employment is very large. Depending on the value of θ, firing costs of anything from 1.6 to 4 quarters' wages may be observationally equivalent in this sense. This suggests that a complicating factor when trying to obtain clear empirical results on dismissal costs may be their sensitivity to variations in the treatment of exiting establishments. Thus, although this paper argues that dismissal costs on exit are most likely small, further empirical documentation of this claim could be interesting.
Interestingly, dismissal costs discourage job creation and encourage the role of plant turnover in job turnover, even when θ is adjusted so that employment remains unchanged. This underlines the importance of the composition effect, and the link between this effect and the size of θ.
Discussion: Contract Incompleteness and the Lifecycle
The EPL literature often finds that dismissal costs can affect labor market performance, through employment-to-population ratios or unemployment rates. At the same time, Akerlof and Miyazaki (1980) suggest that a certain level of severance pay forms part of an optimal labor contract under certain circumstances. Hence, mandated severance pay below these levels should have no impact on employment outcomes. Moreover, as underlined by Lazear (1990), mandated severance pay above what would be agreed on voluntarily should be “undone” by an appropriately specified contract.
There are indeed examples of such behavior. For example, Holzmann et al. (2003) finds that in some countries companies may purchase insurance to cover severance payouts. In this event, although the burden of severance pay falls on employers, severance pay no longer plays the role of a direct dismissal cost. There also may be loopholes in the manner in which EPL is implemented.25
For instance, Posthuma et al. (2000) mention that in Mexico it was not uncommon for workers to sign resignation letters on being hired, so that employers could fire them and reduce the dismissal cost by arguing to the regulator that the dismissal was in fact a voluntary quit.
On exit, previously agreed contracts may no longer be enforceable. At that point, whether the employer can make promised severance payments will be constrained by solvency, regulatory provisions, and perhaps ownership structure. Which contracts are or are not paid then becomes a judicial matter. Indeed, Lazear (1990) conjectures that the declaration of bankruptcy could be a way for employers to void previously agreed contracts. This is equivalent to suggesting that contracts are incomplete solely to the extent to which they do not bind on exit.
What would the world look like if exit were the only margin of contract incompleteness? Quantitatively, the model can be used to address this question in two ways. As we shall see, it turns out that the assumption of contracts being complete except on exit has counterfactual implications.
First, consider the following thought experiment. Suppose that the optimal labor contract implies a severance payout of four quarter's wages. Mandated severance payments of τ≤4 will thus make no difference to the behavior of continuing establishments. However, what happens on exit does depend on mandated costs τ—and, of course, on θ. In this case,

Hence, if θ is constant across countries at some fixed level
, the effects of varying τ∈[0, 4] are identical to the effects of varying
as represented in Figure 5. Thus, mandated severance pay would be associated with a decrease in employment and a decrease in steady-state consumption as before. Observe that, in this case, θ and τ can no longer be separately identified. Thus, to the extent that there is voluntary severance pay, variation in θ may obscure results obtained by using measures of EPL that ignore θ.
Second, suppose that the optimal privately agreed severance payment is zero and, following Lazear (1990), workers and employers can “undo” mandated severance pay contracts. Equivalently, one might argue that labor contracts are set in such a manner that severance pay does not cause any direct rigidities, for example, by buying insurance. Again, this will only be true at continuing establishments: payments made by exiters will depend on legal and regulatory provisions as well as the intensity of EPL. This is equivalent to setting

so that, in the final analysis, only exiting plants need pay dismissal costs.
The results of varying θ—with dismissal costs τ=4 fixed but only impacting exiters—are reported in Figure 7. Even if continuing plants can avoid dismissal costs, firing costs of one year's wages can still lead to up to a 3% employment drop in the model.

Dismissal costs only on exit.
Alternatively, Figure 7 can be interpreted as having θ=1 fixed and varying τ from zero to four—recall that θ and τ cannot be separately identified now. As before, increasing dismissal costs decreases employment and consumption, solely because of apprehension in hiring induced by the risk of exit.
Observe that, in both these scenarios of complete contracts at continuing establishments, dismissal costs decrease the importance of entry and exit for job turnover. For instance, in Figure 7, an increase in θ (or in τ) decreases the influence of both entry and exit in the lower two panels. From a theoretical perspective this is not surprising because, by assumption, exit is the only margin along which EPL can have an effect. However, it contradicts the empirical findings of Blanchard and Portugal (2001) regarding this relationship. Thus, assuming that those findings are robust, the model suggests that some sort of market incompleteness related to EPL must affect continuing establishments also.
For example, although in some countries there exists insurance against severance pay claims, this class of claims may be subject to severe problems of asymmetric information that reduce the scope and usefulness of this kind of insurance. Adverse selection would be likely, unless all firms are obliged to purchase such insurance. In any case, identifying the sources of market incompleteness is an interesting topic for further work.
Concluding Remarks
Employment protection institutions have been emphasized in accounts of labor market differences between the United States and Western Europe. However, the impact that these may have on exit has not been investigated. The paper shows that a model in which exit provides relief from dismissal costs is consistent with empirical findings on the relationship between EPL and role of entry and exit in job turnover. Moreover, the employment effects are almost halved if failing establishments are exempt from dismissal costs. The broader points are that policy analysis with heterogeneous agents is highly sensitive to the endogeneity of the type-space, and that legislation that affects what happens on exit may have significant aggregate effects.
The model departs as little as possible from the related literature to ensure comparability of results. In particular, this implies that there is no welfare-improving role for dismissal costs in the model. The virtue of such a framework is that it serves as a useful benchmark.26
This does not mean that there is no role for EPL in the model, however, as it could have redistributive implications, as in Saint-Paul (2002).
Finally, one of the reasons that EPL is effectively lifted on exit is that exit may occur in situations of insolvency. Thus, EPL may affect the optimal capital structure, a channel that to the author's knowledge has not been identified in the literature.
APPENDIX A. PROOFS
Proof of Proposition 1. Let v be a continuously differentiable function. Define

where C(zt, nt) is the expected continuation value of the firm, given by
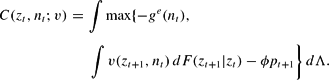
and B is the Bellman operator. Standard recursive methods imply that V is the unique fixed point of B. Finally it is simple to show that if v is decreasing in ϕ and increasing in z then Bv is too which, by Theorem 3.2 and Corollary 1 of Stokey et al. (1989), implies that V shares these properties. Since there is a one-to-one mapping between z and size in the benchmark economy, the result follows.
LEMMA 1. μ* exists and is unique.
Proof. Equation 3, Assumptions 1 and 2, and Proposition 1 imply that Γ satisfies the monotonicity assumptions of Theorems 1 and 2 from Hopenhayn and Prescott (1992).
Proof Proposition 2. Define a sequence
equal to E*. Let μ0=Eψ, and define a sequence of measures μt+1=Γ(μt). Define Mt=μt/∫dμt, so that Mt is a cdf describing the distribution of types by age t. Assumptions 1 and 2 and Proposition 1 imply that27
Dependence of Mt on n is suppressed because n does not matter for decision variables in the benchmark economy.
, in other words
is an increasing sequence. The result follows from the monotonicity of X, since the hazard rate for each age group equals 1−∫Λ[∫V(z′, n) dF(z′|z)] dMt and V does not depend on n in the benchmark economy.
Proof of Proposition 3. Follows from the proofs of Propositions 1 and 2.
APPENDIX B. CALIBRATION DETAILS
B.1. BENCHMARK CALIBRATION
This Appendix describes the calibration procedure in greater detail.
To begin, I choose Φ={0, ϕ, ∞} and Λ={λ0, λϕ, λ∞}, λ0=1−λϕ−λ∞. This nests the exit models of HR and of Veracierto (2001). In the former there is a fixed cost of operation, corresponding to the case Λ={0, 1, 0}. In the latter the hazard rate is a parameter, corresponding to the case Λ={1−λ∞, 0, λ∞}, for some λ∞<1.28
The disadvantage of the HR structure is that exit is highly concentrated among the youngest establishments. For example, although it matches the overall hazard rate, the quinquennial model of Hopenhayn and Rogerson (1993) displays a 64% hazard rate for young plants, well above the 39% found in the data. When period length is shorter the implied differences between model behavior and the data are even greater, leading Veracierto (2001) to impose the exogeneity of establishment exit. However, when the endogenous response of exit rates may be an important determinant of aggregate dynamics, exogeneity is restrictive. Generalizing Φ and allowing its parameters to be determined via calibration will allow me to allocate hazard rates over the plant lifecycle and the size distribution in a manner that is quantitatively accurate. The fact that other models are special cases of the present model also allows me to explore which features do or do not matter quantitatively for the effects of dismissal costs, an issue I explore below.
Productivity shocks z are drawn from a discrete grid of 20 points over the real line. Given a particular grid, multiplying it by any factor affects only the size and not the relative composition of the economy, so all that matters for calibration are the upper and lower bounds relative to each other. I choose an upper value of one. The lower value is
, which I take as an additional parameter. Thus, the possible shocks are
, where
. In turn, I allow labor input to be drawn from a grid of 200 discrete values. Some experiments were repeated for grid values up to 2000, yielding results that were similar although more burdensome to obtain.
The distribution of idiosyncratic productivity shocks F is given by an AR(1) process with normal disturbances,29
To be precise, it is a censored normal since idiosyncratic shocks are drawn from a bounded interval. This assumption is necessary for proving Lemma 1.
. Note that ν is overspecified and cannot be pinned down, amounting to another normalization on the size of the economy. Hence, I choose ν so that it is centered over the grid of shocks. If zμ is the geometric mean of
given the unconditional distribution F*, then ν=(1−ρ)log zμ.
I set ψ to be a uniform distribution over the lower portion of the grid up to some level
. Assumption 2 is satisfied so long as
is sufficiently low.
I set the functional form of the managerial technology to
. It is not clear what the empirical counterpart of m is; hence, I pick
so that it is small.30
Veracierto (2001) mentions that a small value of ζ is necessary to generate realistic fluctuations at business cycle frequencies. In this and in the investment-to-capital ratio I follow that paper as it also uses quarterly data and thus serves as a quantitative link to the related literature.
, which leaves about 1% of employment in the “managerial” form. Values between 0.2 and 0.05 yield similar results.
I assume that labor is indivisible, so that all agents are either working time 1 or not working at all. This enables a simplified representation of household preferences in the following manner, for a constant ϒ:

This assumption has a number of convenient properties that I outline below. It is also made by Hopenhayn and Rogerson (1993), so it enables a direct comparison of results.
The assumption of indivisible labor is consistent with the fact that most of the time series variation in employment is along the extensive rather than the intensive margin (number of workers vs. hours per worker). This assumption is also known to endow related models with an intertemporal elasticity of substitution that is consistent with aggregate data, while being independent of microeconomic estimates of the structure of U itself. By contrast, the behavior of aggregate data over the business cycle is not consistent with these microeconomic estimates. On these points, see Hansen (1985) and Rogerson (1988).
With indivisible labor, agents may not all receive the same allocations in equilibrium. Even then, however, the indivisibility implies that the elasticity of the aggregate labor supply curve will be the same: Rogerson (1988) proves that the aggregate economy behaves as though there were a representative agent with preferences as in 12, even though no single agent actually has these preferences. Thus, heterogeneity does not affect the behavior of the labor market.31
An implication of this result is that whether firing costs take the form of a firing tax—as in the related literature—or severance pay does not affect the behavior of the labor market, even though it may have redistributive implications.
Since heterogeneity would significantly increase the computational complexity of simulations, and since it does not affect aggregate behavior, I make a further assumption to abstract from it. Rogerson (1988) shows that a mechanism involving tradeable lotteries allows agents to receive identical allocations in equilibrium, so that equation (B.1) does in fact reflect household preferences, where ht+mt is expected labor input.32
Other assumptions that deliver the same result are that perfect unemployment insurance is available, or that households are composed of a continuum of agents and that preferences are defined over household averages rather than individual outcomes, as in Veracierto (2001).
Incidentally, the MP framework distinguishes between the allocations of employed and unemployed workers: however, it makes the strong assumption of forbidding agents from saving, so its redistributive implications should be treated with caution.
I choose the dis-utility of labor ϒ so that employment is approximately 80%. β is chosen to match an annual interest rate of 4%, which is common in the real business cycle literature. Factor shares αk and αn are taken from the NIPA accounts. The value for αn chosen is an intermediate value among those measured. The value of αk implies that 12% of GDP goes as direct profits to owners, which is approximately what we observe by adding profits, dividends and interest income in the United States National Income and Product Accounts. Depreciation δ is computed from the first order conditions using the equation δ=K/I+1−γ. This leads to an average age of capital of 17 years, close to the value of 20 years observed in the NIPA tables.
The autocorrelation of the size of surviving establishments after T quarters is ρT. The Census of Manufactures—a quinquennial data set—yields a quinquennial autocorrelation of 0.93, so that ρ=0.931/20. As a result, idiosyncratic productivity is highly persistent. Because size is closely related to productivity in the model, this implies that size is also persistent, a feature that is well documented by, for example, Evans (1987).
The remaining six variables are chosen so that establishment size and hazard rates are distributed across the lifecycle in a manner consistent with plant level data.34
The algorithm used is simulated annealing: see Bertsimas and Tsitsiklis (1993).
and
. The six statistics that I match are:
- The 5-year exit rate;
- The 5-year exit rate of establishments aged 6 years or less;
- The proportion of establishments aged 6 or less that are “small”—by this I mean they employ 30% or less than the average;
- The proportion of employment that is accounted for by job creation in each quarter;
- The proportion of job creation due to birth;
- The proportion of job destruction due to exit.
B.2. COMPARISON WITH THE LITERATURE
The model differs in five ways from that of the seminal HR paper:
- Exit: Although HR has endogenous exit, exit is not an important margin of adjustment in that paper, because of the manner in which exit is formulated and/or because there are only 10 shock values.
- Capital: In HR, the number of plants is endogenous, but the capital stock at each plant is fixed at one.
- Fineness: In HR, the grid of productivity shocks is coarser than here.
- Period length: For calibration, HR uses quinquennial data. I use quarterly data, as does Veracierto (2001).
- Entry structure: in the current model the entry technology is strictly concave—as in Veracierto (2001)—whereas in HR it is linear.
To find the source of these quantitative differences, I recalibrated the model after removing each of these features, and performed identical policy experiments upon each variant, setting (τ, θ)=(4, 1) as before. Results are reported in Table B.3. A brief discussion of the recalibration procedure is reported at the end of this section.




B.3. RESULTS
- Model A is a version of the current model, but without capital nor endogenous exit. This is equivalent to the HR setup, except that it is quarterly. The compensating variation is about the same, but the employment and consumption response of the economy is considerably larger. This suggests that period length may be quantitatively important.
- Model B has an intensive margin for capital, but exit is exogenous. Veracierto (2001) studies a model equivalent to Model B, with the same entry structure but with only nine shock values. A comparison between Tables 5 and B.1 finds that Model A, Model B, and the Veracierto (2001) model all behave in a quantitatively similar fashion. This suggests that the fineness of the grid is not very important.
- The last column, Model C, is the benchmark economy. The responses of employment and consumption are particularly strong compared to Models A and B. This suggests that endogenizing exit is quantitatively important.
- Finally, the model differs from the HR setup in that the indifference condition on entry involves a strictly concave production function rather than a linear function. Samaniego (2001) presents a quinquennial vintage capital model that reduces to the HR setup for a certain parametrization, except for entry structure which is as in the current framework. The quantitative behavior of that model is close to that of the HR model, suggesting that the entry structure is not quantitatively important.
To conclude, endogenizing the exit margin appears to be an important determinant of the response of the economy to dismissal costs. Observe that the exit rate decreases by about 4%. Although this change in hazard rates is not large, its influence is magnified by the fact that plants of “marginal” types that would have exited in the absence of mandated dismissal costs are likely to suffer repeated continuation shocks, since productivity is highly persistent. This a second reason why the economy responds more strongly when establishments can respond along the exit margin: the establishment distribution can vary substantially more than hazard rates. The average idiosyncratic shock value decreases by about 10%. This contrasts with Model A and Model B, in which the average z value does not change by construction because exit is exogenous and, hence, resource misallocation is the only source of inefficiency.
I also find that quarterly models respond more strongly to dismissal costs. This is for two reasons. First, quarterly models entail more small negative idiosyncratic shocks over time that are discounted less heavily than if no shocks occurred for 5 years. Second, quinquennial job flow statistics “miss” a lot of job turnover that occurs over shorter time frames. For example, a plant that suffers a “reversal of fortune,” firing part of its workforce and then gradually hiring them back within a 5-year period as a result of favorable productivity shocks will not generate any job flows in quinquennial data. Hence, calibrating the model to quarterly job flows increases the measured impact of firing costs.
B.4. RECALIBRATIONS
To examine the importance of different margins of adjustment, I calibrated three different versions of the model:
- Model A: Exit is exogenous and the quantity of physical capital is constant across plants (similar to HR);
- Model B: Exit is exogenous and the quantity of physical capital is endogenous at each plant (similar to Veracierto 2001);
- Model C: Exit is endogenous and the quantity of physical capital is endogenous at each plant (this is the benchmark economy).
In Table B.4 I report the parametrizations used for each model; Table B.5 reports summary statistics used in calibration. The important ones to vary across models are those that govern exit and the idiosyncratic productivity process. When capital is exogenous (Model A), a larger dispersion of shocks is required to match the same magnitude of job flows, as the absence of capital ties the plants' hands and reduces the effect of a given change in productivity on size. This is seen in that in Model A
and
are much lower than in the other two models, whereas σ is much larger.


When exit is exogenous (Models A and B), λ3 is chosen to match the overall exit rate, whereas ϕ and λ2 are set to zero. This means that the other two statistics related to exit—exit among the young and the extent of job destruction because of exit—cannot be matched. Table B.5, shows that this results in exit accounting for an excessive portion of job destruction, as it is distributed evenly across establishments of different sizes, whereas it should be concentrated among the small—although not too much so.
The author would like to thank Pamela Labadie, Gordon W. Johnson, the Editor, and two anonymous referees, as well as participants at the GWU Macro-International seminar, the 2003 Midwest Macro Meetings at the Federal Reserve Bank of Chicago, and the 2003 Meetings of the Society for Computational Economics at the University of Washington for their suggestions and insights. The usual disclaimer applies.