Published online by Cambridge University Press: 10 June 2004
This paper provides evidence that domestic opportunities to share risk have contributed to slower growth. We first provide a simple model economy that demonstrates how a country's ability to diversify risk is linked to its growth rate. In the context of the model economy, we then investigate empirically whether there is any systematic relationship between domestic opportunities to diversify risk and growth. We employ two econometric procedures: (1) traditional instrumental variables estimation and (2) dynamic panel methods. Interpreted in the context of the model economy, the empirical analysis reveals a robust negative relationship between domestic opportunities to diversify risk and both capital stock and output growth.
This paper provides evidence that domestic opportunities to share risk have contributed to slower growth. A large literature investigates the relationship between risk sharing and growth. Much of this work has focused on the effects of global diversification. In a seminal contribution, Obstfeld (1994) demonstrates that international asset trade may induce a portfolio shift away from low-risk, low-productivity investments into high-risk, high-productivity investments. As a result, expected consumption growth increases. In contrast, Devereux and Smith (1994) show that international asset trade, and its attendant reduction in risk, may lead to a decline in saving for precautionary purposes. As a result, expected growth decreases. These contributions, and numerous others, assume that financial markets span the space of shocks to national output. As a result, all countries generally hold identical portfolios of risky assets in equilibrium, and growth rates differ across countries only to the extent that tolerance for risk varies. In reality, however, countries do not hold identical portfolios of risky assets, in part because markets for sharing risk are far from complete, and the risks associated with a substantial fraction of wealth are nontradeable. Thus, some of the differences in growth rates observed across countries may be attributable to differences in opportunities to diversify risk. In addition, documented home bias in portfolio holdings and lack of consumption correlation across countries indicate that little international risk sharing occurs. Differences in cross-country growth rates attributable to risk sharing may therefore be largely due to differences in domestic opportunities to diversify risk. To explore this possibility, we first provide a simple model economy that demonstrates how a country's asset payoff structure, and its ability to diversify risk, are linked to its growth rate. In the context of the model economy, we then investigate empirically whether there is any systematic relationship between domestic opportunities to diversify risk and growth.
According to portfolio theory, a key determinant of one's ability to diversify risk is the extent to which the payoffs to available assets covary. Conventional wisdom suggests that the extent of covariation across payoffs is negatively related to the expected return on a portfolio—low correlation between returns reduces portfolio risk and allows agents to invest in riskier, more productive assets. In other words, diversification opportunities lead to an increase in the expected growth of wealth. However, diversification opportunities may also be negatively related to the expected return on a portfolio. Consider, for example, an individual with two risky investment opportunities. Suppose further that both assets are equally volatile, but that one offers a higher expected return. In this context, the sole purpose of holding the two assets in combination is to reap diversification benefits due to less than perfect correlation of returns. Furthermore, given the asset payoff structure described, an increase in the correlation of returns would lead to an investment portfolio shift toward the asset with the higher expected return. In other words, a decrease in diversification opportunities would lead to an increase in expected growth of wealth. Likewise, an increase in diversification opportunities would lead to a decrease in growth. Thus, a negative relationship may exist between diversification opportunities and growth.
Over the course of the last century we have observed an increase in the extent of global integration, and presumably in risk-sharing opportunities, coincident with impressive growth performance. Casual observation thus suggests that conventional wisdom and Obstfeld (1994) had it right; there appears to be a positive link between global risk sharing and growth.1
I thank an anonymous referee for bringing this observation to my attention.
Other authors have explored the implications of agents' ability to diversify risk while holding multiple assets. In the context of the home-bias literature, Bottazzi et al. (1996) measure the extent to which two broad categories of domestic assets covary: nontraded human capital and traded physical capital. This distinction is important in the context of the home bias puzzle; if human capital returns are more highly correlated with returns in the domestic stock market than with returns in foreign stock markets, then the risk associated with human capital can be more effectively hedged with foreign securities than with domestic ones. An alternative approach to categorizing domestic assets, which does not rely exclusively on the distinction between human and physical capital, is adopted here. The model economy described in the next section is characterized by two distinct sectors of production: a corporate sector and a noncorporate sector. Claims to the profits from the corporate sector are assumed to be traded on a stock market. Income generated in the noncorporate sector is assumed to accrue directly to households. Agents have several investment opportunities: They may invest in physical and human capital used in the corporate sector as well as in physical and human capital used in the noncorporate sector. This approach indirectly captures the possibility that returns to nontraded human capital and traded physical capital may be less than perfectly positively correlated. In addition, this approach admits the possibility that financial claims may not be traded on the returns from a country's entire physical capital stock, and that the capital used in various sectors of the economy may be distinct. The division of the economy into two sectors also allows for the construction of returns from data that are widely available—national accounts and stock market data.2
The categorization of assets according to sector does have a drawback—it makes the source of covariation between assets difficult to identify. For example, a negative correlation between returns in the noncorporate and corporate sectors could be attributable to a negative covariance between wages and returns to financial assets and/or to a negative covariance between returns to nontraded physical capital and returns to financial assets, and/or to a negative covariance between wages and returns to nontraded physical capital. Unfortunately, the data necessary to disentangle these possibilities (data on employee compensation and data on nontraded physical capital and its productivity) are not available for a broad cross section of countries.
To evaluate empirically whether there is any systematic relationship between domestic opportunities to diversify risk and growth, we employ two econometric procedures: (1) traditional instrumental variables estimation of the data in cross section, and (2) dynamic panel methods. A primary objection to traditional cross-country growth regressions is that the results may be biased by endogeneity of regressors and omitted variables. Generalized method of moments dynamic panel techniques can be used to control for bias from both of these sources, and are becoming increasingly common in the empirical growth literature as expanding data sets have allowed researchers to employ these methods.3
Dynamic panel methods do present some drawbacks in the context of empirical growth work. In particular, although use of a panel allows one to extract information from the time-series dimension of the data, it may confound long-run growth effects with business-cycle movements. We therefore present the results produced by both types of estimators.Interpreted in the context of the model economy, the results of the empirical analysis reveal a robust negative relationship between domestic opportunities to diversify risk and both capital stock and output growth. Both the cross-section instrumental variables estimator and the dynamic panel estimator produce similar results, indicating that the relationship revealed is not attributable to biases due to endogeneity or omitted variables such as country-specific effects. The results are robust to changes in the conditioning information set.
The remainder of the paper is organized as follows: Section 2 provides a model economy sketch used to inform data measurement and highlights the relationship between risk sharing and growth. In Section 3, data and measurement are discussed. In Section 4, methodology is reviewed. Empirical results are presented in Section 5. Section 6 concludes.
The principle underlying the relationship between risk sharing and growth explored in this paper is straightforward and well known: One's ability to diversify risk depends on the extent to which available assets covary. The structure of a model economy is nonetheless required to inform the measurement of returns and their correlation. In this section, we therefore sketch a model economy that provides a basis for the empirical investigation of the relationship between risk sharing and growth.
Imagine an economy in which output is produced in two sectors—a corporate one and a noncorporate one. In both sectors, physical capital, labor, and human capital combine to produce output according to a standard neoclassical production technology, with Yt=Yc,t+Ync,t=Ac,tKαc,t(Lc,tHc,t)1−α+Anc,tKαnc,t(Lnc,tHnc,t)1−α, where K, H, and L denote physical capital, human capital, and labor, respectively; A denotes a stochastic productivity shock; and the subscripts c and nc denote items specific to the corporate and noncorporate sectors, respectively. An infinitely lived representative household supplies human capital and labor (inelastically) to both sectors. It invests directly in the noncorporate sector by supplying physical capital and indirectly in the corporate sector by purchasing equity shares. The corporate sector is assumed to consist of a single stock company. The investment, employment, and dividend policies of the stock company are set by a manager whose objective is to maximize the present value of dividends. Krebs and Wilson (2004) show that an equilibrium exists for such an economy in which the household's problem of choosing how much human capital to supply to both sectors, how much to invest in physical capital in the noncorporate sector, and how many equity shares to purchase reduces to a standard intertemporal portfolio choice problem of the Merton type [Merton (1969, 1971)], with two risky assets. In other words, the household's problem reduces to a consumption/saving decision, and a choice of what fraction of its wealth to invest in the noncorporate sector and what fraction of its wealth to invest in the corporate sector.
More formally, assuming the household has preferences over stochastic consumption sequences {Ct}∞t=0 that allow for a time-additive expected utility representation with logarithmic one-period utility function, the household's problem is
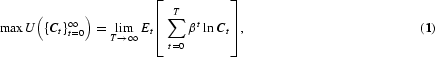
subject to
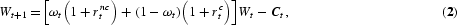
where β∈(0, 1) denotes the discount factor; Wt denotes wealth at time t that consists of human capital invested in both sectors, physical capital invested in the noncorporate sector, and equity shares; ωt and 1−ωt are the time t shares of wealth invested in the noncorporate and the corporate sectors, respectively; and rnct and rct denote the time t returns to investing in the noncorporate and corporate sectors, respectively.
In addition to providing guidance with respect to measurement, the division of the economy into two sectors captures the notion that the return on domestic financial assets (the return to investment in the corporate sector of the model economy) may not be perfectly correlated with aggregate income movements, or the return on a portfolio of investment in both the first and second sectors. The notion that this correlation is likely to be less than perfect underlies the establishment of the “macro markets” proposed by Shiller (1993). Shiller has proposed the creation of an array of risk markets—macro markets—for claims on major components of national incomes. His proposal stems from the observation that most risks borne by individuals cannot be shed in existing financial markets. The question of interest in this paper, is whether or not there is evidence that the extent of correlation between the return on domestic financial assets and aggregate income movements affects a country's growth rate, and whether that effect is positive or negative.
DEFINITION 1. A return process,
, is said to “strictly dominate” another return process,
, if
and
where
and
denote the standard deviations of the return processes. A return process
, is said to dominate another return process,
, “in terms of mean,” if
and
. A return process
, is said to dominate another return process,
, “in terms of standard deviation,” if
and
.
Claim 1. All else equal, if returns in either sector strictly dominate or dominate sufficiently in terms of mean, then the greater (smaller) the contemporaneous correlation between returns in the two sectors, the greater (smaller) the economy's growth rate. Otherwise, the greater (smaller) the contemporaneous correlation between returns, the smaller (greater) the economy's growth rate.
Proof. The above claim is easily demonstrated by examining the household's optimal consumption rule and portfolio choice. The household's optimal consumption rule for its standard intertemporal choice problem is
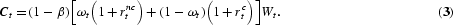
It follows that the expected growth rates of the total capital stock and of output are
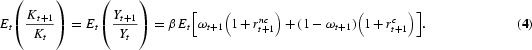
The household's Euler equations dictate that the portfolio share, ωt+1, solves
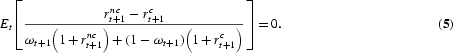
Assuming returns have a bivariate normal distribution that is i.i.d., their moment generating function and the approximation ln[ωt+1(1+rnct+1)+(1−ωt+1)(1+rct+1)]≈ωt+1rnct+1+(1−ωt+1)rct+1 can be used to explicitly determine the household's optimal portfolio choice.
4The portfolio choice will be time invariant, given the assumption of i.i.d. returns. Therefore, we henceforth drop the time subscripts.
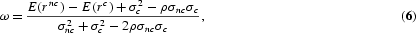
where σnc, σc, and ρ denote the standard deviation of returns in the noncorporate and corporate sectors, and the contemporaneous correlation between returns, respectively. Given this portfolio choice, it is easy to verify that the growth rates of the total capital stock and of output are increasing in ρ if E(rnc)>E(rc) and 2[E(rnc)−E(rc)]+σ2c−σ2nc>0 or if E(rnc)<E(rc) and 2[E(rnc)−E(rc)]+σ2c−σ2nc<0. Otherwise, the growth rates are decreasing in ρ.
In theory then, an economy characterized by an asset payoff structure that allows substantial diversification opportunities, as measured by the correlation between returns, may grow faster or slower than an economy with more limited diversification opportunities.
Given data at the sector level, one could infer the asset payoff structures of a cross section of countries, use the above result to determine whether the model predicted any systematically positive or negative relationship between risk-sharing opportunities and growth, and then test this prediction empirically. Unfortunately, data that distinguish between output in the noncorporate and corporate sectors are not available for a large number of countries. As a result, one cannot directly examine whether or not there is a systematic relationship between the correlation of returns across the two sectors and growth. However, as described in Section 3.2, a measure of returns in the corporate sector is available—a broad index of stock returns—and on the basis of the model economy outlined above, one can construct a measure of the weighted average of returns across the two sectors. The correlation between the weighted average of returns to capital in the two sectors and stock market returns is ρk,c=(E{[ω(1+rnc)+(1−ω)(1+rc)](1+rc)}−E[ω(1+rnc)+(1−ω)(1+rc)]E[(1+rc)])/(σkσc)={ω(ρσncσc−σ2c)+σ2c}/(σkσc), where σk is the standard deviation of the weighted average of returns to capital in the two sectors, and all other notation is as previously defined.
This correlation is of interest because, unlike the correlation between returns in the two sectors, it can be measured. Unfortunately, while ρk,c is a function of ρ, the relationship between the two correlations is not systematically positive or negative; it depends on an economy's asset payoff structure. The relationship between ρk,cσk and ρ may likewise be positive or negative, but we focus on it since it is easier to sign. Despite the general ambiguity, the data indicate that the variable ρk,cσk may nonetheless be a useful measure of risk sharing. In all but two of eight cases, the relationship between ρk,cσk and ρ is positive (see Appendix A for proof). The relationship may be negative if returns in neither sector strictly dominate returns in the other and returns in one sector sufficiently dominate in terms of standard deviation. In particular, if
then ρk,cσk may be decreasing in ρ.
As discussed below in Section 3.2, the majority of countries in the sample are characterized by returns in the noncorporate sector that strictly dominate returns in the corporate sector. However, there are several countries (7 of 36) in which returns in the corporate sector dominate in terms of mean. Two of these countries (Finland and the Netherlands) have asset payoff structures consistent with case (i) above.5
Figures mentioned for the number of countries (7 of 36 and two) are for the baseline case parameterization.
Thus, with only two exceptions, the asset payoff structures of the countries for which data are available are likely consistent with a positive relationship between ρk,cσk, a measurable variable, and ρ, the unmeasurable variable of interest. The empirical analysis that follows therefore examines whether or not there is a systematic relationship between ρk,cσk and growth, conditional on the other features of a country's asset payoff structure. Evidence of a positive (negative) relationship is interpreted in the context of the model economy as indirect evidence that a decrease in risk-sharing opportunities—an increase in the correlation of returns—is associated with an increase (decrease) in growth.
The model economy sketch identifies a single source of risk-sharing opportunities: covariation of returns across sectors. Within-sector diversification may also be an important determinant of growth. Within-sector diversification opportunities may affect growth via their impact on sector-specific expected returns and also via their impact on the standard deviation of sector-specific returns. It is unclear whether one might expect within-sector risk sharing to have much power to explain cross-country growth differentials. On the one hand, there may not be much variation across countries in within-sector diversification benefits. Conventional wisdom—and many textbooks—suggest that diversification benefits are largely exhausted with a portfolio of 10–15 stocks. Statman (1987) argues for a higher number and indicates that a portfolio of roughly 30–40 randomly selected U.S. stocks is well diversified. Even this higher figure suggests that a relatively small number of stocks is required to achieve significant risk sharing. Thus, it seems likely that across countries, a sufficient number of firms exists in each sector to achieve nearly maximum within-sector diversification. As a result, cross-country variation in within-sector risk sharing may be limited. On the other hand, it is well known that households do not appear to hold well-diversified portfolios and that their holdings vary substantially from those suggested by Markowitz's portfolio selection model. As a result, in practice, cross-country differences in the extent to which within-sector diversification opportunities are exploited may be related to cross-country differences in growth. To control for this possibility, and to isolate the impact of across-sector diversification on growth, average returns to capital and average stock returns are included in the regression analysis as proxies for within-sector diversification opportunities. The standard deviation of returns to capital and the standard deviation of stock returns are included as regressors as well.
This section describes the data used in the empirical analysis and its application in the context of the model economy sketch presented in Section 2. More specifically, we describe the construction and measurement of (i) the growth indicators, real per capita GDP, and capital stock growth; (ii) returns; and (iii) risk-sharing opportunities. The sample includes a total of 36 countries, 16 developing and 20 developed nations. A detailed list of countries included in the sample, along with data sources for all of the variables used, can be found in Appendix B.
The variable “output growth,” listed in the tables, stands for the growth rate of real per capita GDP. It is constructed using data on nominal GDP, the GDP deflator, and population from the IMF's International Financial Statistics. In the cross-sectional analysis, output growth is the average annual geometric growth rate of real per capita GDP over the period 1976–1999, or over the period for which data are available. Similarly, for the dynamic panel analysis, output growth is the average annual geometric growth rate of real per capita GDP over the periods 1976–1979, 1980–1984, 1985–1989, 1990–1994, and 1995–1999.
The variable “capital growth” equals the growth rate of the real per capita capital stock. It is constructed using data on investment, GDP, the GDP deflator, and population from the IMF's International Financial Statistics. As with output growth, in the cross-sectional analysis, capital growth is the average annual geometric growth rate of the real per capita capital stock over the period 1976–1999, or over the period for which data are available. Similarly, for the dynamic panel analysis, capital growth is the average annual geometric growth rate of the real per capita capital stock over the periods 1976–1979, 1980–1984, 1985–1989, 1990–1994, and 1995–1999. To compute capital stock growth rates, a capital stock series is first constructed. Construction of the capital stock series requires an initial capital stock estimate. King and Levine (1994) recommend choosing an initial capital stock estimate that is a function of the country's own growth rate over the 1950's, as well as the world growth rate over the past 30 years. We depart from this suggestion in order to obtain a more accurate estimate of the initial capital stock. We first make an initial guess of a country's capital/output ratio. We then compute the implied capital stock series. Next, we compare the initial capital/output ratio guess to the average capital/output ratio implied by the capital stock series for the first 10 years for which data are available (typically, 1948–1958). We then revise the initial capital/output ratio guess and repeat the procedure until the implied average capital/output ratio for the first 10 years of data matches the initial capital/output ratio guess. The capital stock series is computed according to the capital accumulation equation, Kt+1=(1−δ)Kt+nIt, with a depreciation rate (δ) of 7%, and n=0.20 and n=0.25 for developing and developed countries, respectively. The adjustment to the investment term is made because some part of what is counted as private investment in national accounts data is investment in workers. As such, it should be counted as human capital according to our model. To adjust for this discrepancy, we assume that 20% and 25% of investment in developing and developed countries, respectively, consists of investment in human rather than physical capital.
Returns in the corporate sector of the model economy—stock returns—are measured using data on stock price indexes and dividend yields from the World Stock Exchange Fact Book. Annual observations beginning in 1975 (or as early thereafter as data are available) and extending through 1999 are used to compute the mean and variance of stock returns. Returns are deflated using the GDP deflator. We find average real annual stock returns over the period 1976–1999 of 10.6% and 9.9%, respectively, for developing and developed countries. The average standard deviations of real annual stock returns over the period are 45.0% and 24.4%, respectively, for developing and developed countries.
Returns to capital are constructed as follows. Since Yj=AjKαjH1−αj in sector j, the marginal products of capital and human capital in sector j are αAjKα−1jH1−αj and (1−α)AjKαjH−αj, respectively. In equilibrium, these marginal products will be equated, and the marginal product of capital (physical and human) in sector j will equal Ãj=α[(1−α)/α]1−αAj. Thus, in equilibrium, the marginal product of capital distributed across the two sectors of the economy according to the optimal portfolio weights, ω and 1−ω, is ωαÃnc+(1−ω)αÃc, and the return to capital is therefore ωαÃnc+(1−ω)αÃc−δ. Note that in the aggregate, Y/K=ωÃnc+(1−ω)Ãc. Thus, one can use observed output/capital ratios, along with assumed values of α (physical capital's share of income) and δ (the depreciation rate) to construct a series of returns to capital for each country in our sample. Reported results assume α=0.36 and δ=0.07. A depreciation rate of 7% is the rate chosen by King and Levine (1994) and lies between the more common choice of 10% and the value of 5% chosen by Cooley and Prescott (1995). The choice of depreciation rate affects the capital stock series and therefore affects average returns to capital, the standard deviation of returns to capital, as well as the correlation between returns to capital and stock returns. Although the regression results reported assume a depreciation rate of 7%, they are robust to depreciation rates of 10% and 5%. The share of physical capital in output, α=0.36, is a middle-ground choice between a low share of 0.30 and a high share of 0.40.6
The size of α affects the magnitude of average returns to capital, but does not otherwise impact the regression analysis results.
The reported figures for average real stock and capital returns imply that the noncorporate sector of the economy is, on average, more productive than the corporate sector. To illustrate the difference in productivity inherent in the data, consider the following calculation. Assuming that the corporate sector employs 20% of the domestic capital stock, then the developing-country average return to capital of 15.7% and average stock return of 10.6% imply a return to capital in the noncorporate sector of 17.0%. Likewise for the developed countries, an average return to capital of 13.2% and average stock returns of 9.9% imply a return to capital in the noncorporate sector of 14.0%. Qualitatively, these differences are consistent with the view that the most dynamic sector of many economies, and the sector with the highest returns, consists of privately held, often small, firms.
The correlation between the weighted average of returns across the two sectors and stock market returns, ρk,c={ωρσncσc+(1−ω)σ2c}/(σkσc), does not capture the magnitude of the correlation between returns in the two sectors, but if its sign is negative, then the sign of the correlation between returns in the two sectors must also be negative, assuming a strictly positive fraction of the total capital stock is invested in both sectors. In 21 of the 36 countries in the sample, returns in the two sectors covary negatively. Of those 21 countries, 8 are developing and 13 are developed. In the remaining 15 countries, 8 of which are developing and 7 of which are developed, the correlation between the weighted average of returns across the two sectors and stock market returns is positive. It may seem surprising that so many countries in the sample are characterized by returns to domestic assets that comove inversely. This finding is not without precedent however. Bottazzi et al. (1996) report a negative correlation between wages and profits and between human capital and physical capital returns for 12 of 16 OECD countries. Interpreted strictly in the context of the model economy sketched in Section 2, the finding that returns covary negatively in a number of countries suggests either that aggregate shocks affect productivity in the noncorporate and corporate sectors of the economy very differently, and/or that sector-specific shocks covary negatively. More generally, there are numerous reasons one might expect returns to covary negatively. For example, as noted by Bottazzi et al. (1996), shocks that redistribute income across wages and capital may lead to a negative correlation between returns to human capital and returns to financial assets. Short-run price or wage stickiness may likewise lead to interesting comovements in asset returns.
Tables 1A and 1B present summary statistics and correlations for the data in cross section. In these and all other tables, COV stands for ρk,cσk, rk stands for the average return to capital, σk is the standard deviation of these returns, and rc and σc represent average stock market returns and the standard deviation of these returns, respectively. The correlations between each country's stock returns and returns to capital, ρk,c, exhibit substantial variation and range from a low of −0.56 (Spain) to a high of 0.33 (Chile). Stock and capital returns also vary substantially, ranging from lows of −49% (Brazil) and 10% (Switzerland), to highs of 21% (Argentina) and 23% (United States), respectively. Output and capital stock growth observations range from lows of −0.6% (Venezuela) and −0.8% (South Africa) to highs of 6% (Korea) and 8% (Korea). As Table 1B indicates, there is no significant correlation between COV and initial GDP,7
Although not noted in the tables, the same is true for ρk,c. The correlation between ρk,c and initial GDP is 0.002.


This section describes the econometric techniques used to examine the relationship between growth and a country's ability to diversify risk with domestic assets. Following recent empirical contributions to the growth literature, two methods are employed: (i) instrumental variables estimation of the data in cross section and (ii) dynamic panel estimation.
Traditionally, more or less ad hoc cross-country growth regressions have been used to explore the extent to which “policy” differences explain observed differences in levels and growth rates of per capita GDP and per capita capital stocks. Policy differences are typically assumed to be embodied in outcomes such as the black market premium, government spending, inflation, and openness to trade. The variable of interest in this paper is a proxy for the extent of correlation between domestic assets. An exploration of the extent to which this correlation may be under the control or influence of policymakers has not been explored here and is beyond the scope of this paper. Nonetheless, the analysis presented in Section 2 suggests a natural exercise in the spirit of the traditional cross-country growth regression literature: examine whether differences in risk-sharing opportunities across countries have any power to explain differences in growth rates across countries.
To control for simultaneity bias in cross-country growth regressions, instruments are required for any variables suspected to have an endogenous component. Our variable of interest, COV, is derived from returns and, as such, may not be strictly exogenous. In addition, the predicted relationship between COV and growth was derived from a comparative static result, holding constant the means and standard deviations of returns in the two sectors of the economy. These variables, or proxies for them, must therefore be included as regressors, and may also have an endogenous component. As noted above in Section 2, sector-specific returns are also used to control for within-sector risk sharing. In the regression analysis that follows, the mean and standard deviation of stock returns (returns in the corporate sector) enter as regressors, and the mean and standard deviation of returns to capital (the optimal weighted average of returns across the corporate and noncorporate sectors) enter as proxies for the asset payoff structure in the noncorporate sector of the model economy. Lack of suitable instruments has led researchers to frequently employ lagged, or “initial,” values of independent variables as instruments. While lagged values are correlated with the disturbance vector, they are not contemporaneously correlated with the disturbance, assuming the disturbance is not autocorrelated. Initial values of the mean and standard deviation of capital returns are available for use as instruments in the analysis pursued here. However, since our data source provides a record of stock returns beginning only as far back as 1975, initial values of the mean and standard deviation of stock returns and of COV are not available. As a result, other suitable instruments are sought.
Recent contributions to the empirical growth literature suggest a number of possible instruments. Levine et al. (2000) use legal-origin variables developed by La Porta et al. (1997, 1998) as instruments to extract the exogenous contribution of financial intermediary development to growth. Their results suggest that legal origin may be suitable for use as an instrument for COV and/or its conditioning variables, rk, σk, rc, and σc. As Table 1C indicates, there is indeed a statistically significant relationship between COV and the English and French legal-origin variables at better than the 5% and 10% levels, respectively.8
La Porta et al. (1997, 1998) note that commercial laws generally derive from one of four traditions: English, French, German, and Scandinavian. Neither German nor Scandinavian legal origin is significantly related to any of our variables of interest.

Based on the above empirical and theoretical suggestions from existing literature, and the observed significant correlations, we employ the follow instruments for COV, rk, σk, rc, and σc in the analysis that follows: initial values of capital returns and their standard deviations, the English-speaking fraction of the population, latitude, Catholic and Muslim fractions of the population, dummy variables for English and French legal origin, and terms-of-trade shocks.
To create the cross section, data for each country is averaged over the period 1976–1999, producing one observation per country. The regression takes the form
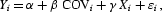
where Y stands for per capita real GDP growth or, alternatively, per capita real capital stock growth; COV stands for ρk,cσc, where ρk,c=correlation between returns to capital and stock returns and σc=standard deviation of stock returns; X is a vector of conditioning variables that control for other factors associated with growth; ε is the error term; and i indexes individual countries.
The cross-sectional results are produced using generalized least squares and the estimates are robust to heteroskedasticity. To extract the exogenous contribution of COV to growth, conditional on the means and standard deviations of stock and capital returns, a vector of instruments, Z, is used. The moment restriction required for (over) identification of the parameters of the model is E[Zε]=0. Satisfaction of this orthogonality condition is assessed with a Hansen test. The Hansen statistic is distributed as χ2, with J−K degrees of freedom, where J is the number of instruments and K is the number of regressors.
We also report results from a dynamic generalized method-of-moments panel estimator. Dynamic panel techniques allow us to better exploit the time-series dimension of the data, to control for the presence of unobserved country-specific effects, and to provide an alternative control for simultaneity bias. Of course, these estimation procedures are not without their drawbacks in the context of empirical growth work. In particular, dynamic panel techniques use instruments based on previous realizations of explanatory variables. To the extent that growth effects may be realized with a delay, the exogeneity of these instruments is questionable. Although we report tests for serial correlation as a check on orthogonality conditions, as Temple (1999) points out, test statistics are not based on the true disturbances, but rather on estimated residuals. In addition, exploiting the time-series dimension of the data may be problematic to the extent that cyclical as well as long-run variation is captured. We therefore view these results as complementary to those produced by the GLS instrumental variables estimator.
Data from 33 of the 36 countries analyzed in the cross-section are available to construct the panel. Annual observations are averaged over five non-overlapping periods (1976–1979, 1980–1984, 1985–1989, 1990–1994, 1995–1999). The resulting panel has a cross-sectional dimension of 34 and a time-series dimension of 5. The basic regression equation takes the form
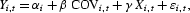
where Y stands for per capita real GDP growth or, alternatively, per capita real capital stock growth; α is an unobserved country-specific effect; COV stands for ρk,cσc; X is a vector of conditioning variables that control for other factors associated with growth; ε is the error term; and i and t index countries and time periods, respectively. The regression is estimated as a stacked system in differences and levels, using the two-step system GMM estimator proposed by Arellano and Bover (1995). Specification of the regression in differences controls for country-specific effects. The regression in levels is added to preserve the cross-country dimension of the data that are lost in the differenced regression. Our sample size is less than ideal because the asymptotic properties of the GMM estimator depend on the cross-sectional dimension of the data. However, Monte Carlo experiments conducted by Blundell and Bond (1998) show that Arellano and Bover's system estimator reduces bias and improves precision in finite samples over the difference estimator alone. The estimates reported are robust to heteroskedasticity.
9The procedures were implemented using Manuel Arellano and Stephen Bond's DPD98 for Gauss. DPD98 for Gauss is a program written in Gauss that computes estimates for dynamic models from panel data, and is available on the Web. Arellano and Bond also provide an easy-to-follow user's guide.
Because the system includes equations in both differences and levels, two sets of moment conditions are imposed. Lagged levels of the explanatory variables are used as instruments in the differenced regression. Assuming that there is no serial correlation in the error term, ε, and that the explanatory variables, COV and X, are weakly exogenous,10
A weakly exogenous explanatory variable may be correlated with current and past realizations of the dependent variables, but must be unrelated to future innovations in the error term.
In this section, we present the results of the cross section and panel analyses described above. To repeat, we are looking for evidence of growth effects attributable to risk sharing. As demonstrated in Section 2 above, evidence of a positive relationship between COV and growth indicates that countries that are better able to diversify risk are growing slower.
Strictly speaking, the model economy dictates that capital stock and output growth are determined solely by COV, capital returns, volatility of capital returns, stock returns, and volatility of stock returns. The model economy is by design an abstraction from reality, however, and there are undoubtedly other important determinants of growth. For this reason, we report several sets of results. Columns 1 and 5 of Tables 2A and 2B report results that assess the strength of the link between COV and capital stock and output growth conditional on only those variables dictated to be important by the model presented. Columns 2 and 6 expand this conditioning information set to include a set of standard state variables included in most cross-country growth regressions: initial GDP, years of schooling, and revolutions and coups. These variables enter as their own instruments. Columns 3 and 7 add a common measure of saving to the state variables—the investment/GDP ratio. This ratio is instrumented with its initial value and with initial values of two other measures of saving from the World Bank's World Saving Database. Finally, columns 4 and 8 expand the conditioning information set further still, by adding four policy variables also common to the growth literature: the black market exchange-rate premium, a measure of government size, inflation, and a measure of openness to trade. These variables are instrumented with initial values.


Columns 1–8 of Table 2A show that COV is significantly and positively related to capital stock growth in both the cross-sectional and panel samples. Interpreted in the context of the model sketched above, these results suggest that per capita capital stock growth has been slower in countries that are better able to diversify risk. For the cross section, the Hansen test of overidentifying restrictions indicates that the orthogonality condition on the instruments is rejected at the 5% level for column 1. Thus, these results should be treated with caution. For the remaining regressions, the orthogonality condition cannot be rejected at the 5% level. For the panel, the p-values on the Sargan test indicate that the instruments used are not correlated with the residuals. The serial correlation tests indicate lack of serial correlation in the error term. The magnitude of the effect of COV on capital stock growth does depend on the conditioning information but is substantial in all cases. The coefficient estimates range from 3.404 to 0.941 in the cross-sectional regressions and from 1.802 to 1.144 in the panel regressions. These results indicate that the relationship between COV and capital stock growth is economically meaningful. For example, the estimated coefficient on COV in column 4, 1.267, suggests that a 1-standard-deviation increase in COV (0.004) would increase real per capita capital stock growth by 0.51% per year. The predicted effects are somewhat smaller in the panel sample. The estimated coefficient on COV in column 8, 1.207, suggests that a 1-standard-deviation increase in COV (0.003) would increase real per capita capital stock growth by 0.36% per year.
As suggested by Devereux and Smith (1994), risk-sharing opportunities may lead to declines in precautionary saving that negatively affect growth. This idea suggests that the relationship between COV and capital stock growth in the data may not be due to optimal portfolio shifts, as suggested by the model sketched, but rather to declines in precautionary saving. As columns 3–4 and 7–8 indicate, the relationship between COV and capital stock growth remains significant when the investment/GDP ratio is added to the conditioning information set of explanatory variables. These results suggest that a relationship exists between COV and capital stock growth that is independent from any relationship between risk sharing and saving and growth that may exist. The results also reveal, however, that the inclusion of the investment/GDP ratio decreases the magnitude of the estimated relationship between COV and capital stock growth. In columns 2 and 6, which do not include the investment/GDP ratio, the estimated coefficients on COV are 2.821 and 1.802, respectively. Once the investment/GDP ratio is added, the estimated coefficients on COV fall to 0.941 and 1.144, as indicated in columns 3 and 7, respectively. Columns 4 and 8 show that further addition of the full conditioning information set results in a slight increase over the estimates in columns 3 and 7, to 1.267 and 1.207. The decline in magnitude of the estimated coefficient on COV when the share of investment in GDP is added to the conditioning information set is consistent with the notion advanced by Devereux and Smith (1994) that there may be a negative relationship between risk sharing and growth via a saving channel. The investment/GDP ratio is perhaps the most common measure of saving used in the growth regression literature, and is one of the few variables for which a robust empirical link with growth has been found [Levine and Renelt (1992), Sala-ì-Martin (1997)]. Several alternative measures of saving from theWorld Bank's World Saving Database were also explored, including two measures of private saving and a measure of national saving. The relationship between COV and capital stock growth are robust in significance and magnitude to the inclusion of the alternative measures of saving in the regression analysis. However, these measures of saving do not appear to be as robustly linked with growth as the share of investment in GDP.
Similar results are reported for output growth in Table 2B. A significant and positive relationship between COV and output growth is revealed, suggesting that those countries that are better able to diversify risk have grown slower. As with the capital stock growth regressions, the null of the Hansen test is rejected for column 1, but not rejected in all other cases considered. For the panel, the p-values on the Sargan test indicate that the instruments used are not correlated with the residuals. The serial correlation tests indicate lack of serial correlation in the error term in columns 5 and 6, but not in columns 7 and 8. Absence of second-order serial correlation is important to ensure the consistency of the dynamic panel estimator. Thus, the coefficient estimates in columns 7 and 8 should be viewed with caution. In the cross section, the coefficient estimate on COV in column 4, 1.526, suggests that a 1-standard-deviation increase in COV would increase real per capita output growth by 0.61%. In the panel, the coefficient estimate on COV in column 8, 1.073, suggests that a 1-standard-deviation increase in COV would increase real per capita output growth by 0.32%. With respect to the additional conditioning variables included in the regressions reported in columns 2–4, we highlight another interesting result. Revolutions and coups, and other variables that proxy for political instability, typically enter negatively in growth regressions. In Tables 2A and 2B, revolutions and coups are significantly positively related to both capital stock and output growth. When the standard deviation of stock market returns is excluded, however, revolutions and coups enter with the usual negative sign. This result suggests that revolutions and coups may have two distinct effects. On the one hand, political instability causes uncertainty and has a negative effect on growth. On the other hand, volatility aside (controlled for in the regression by stock market volatility), political instability may constitute movements toward more efficient allocations of resources (i.e., movements away from unstable allocations outside the core of an economy toward stable allocations in the core).
Also unusual in the results in Tables 2A and 2B is the fact that initial GDP often does not enter significantly and that years of schooling enters significantly negative in several cases. When the variable rk is removed, initial GDP and years of schooling enter with their typical significantly negative and positive signs, respectively. Other coefficients are not substantially affected by the removal of rk.
A large literature has established that there is a strong, positive relationship between financial intermediary development and growth, and between financial market development and growth.11
See for example, Beck et al. (2000), Levine et al. (2000), Levine and Zervos (1998), Rajan and Zingales (1998), and King and Levine (1993).
This paper has explored the effect on growth of opportunities to diversify risk with domestic assets. Interpreted in the context of the model economy presented, the results of GLS instrumental variables estimation of a cross-country sample indicate that in countries where individuals are better able to diversify, growth has been slower. The results of a GMM dynamic panel estimator that controls for simultaneity and omitted variables bias are similar. The negative relationship revealed between risk sharing and growth cannot be entirely attributed to differences in savings, suggesting that optimal portfolio differences may be the source. Evidence that diversification is associated with greater investment in less productive assets across countries contrasts with the notion advanced in the literature on international risk sharing that diversification may lead to portfolio shifts toward more productive assets. We note, however, that the evidence reported here of a negative relationship between domestic opportunities to diversify risk and growth does not contradict or conflict with the possibility that international asset trade may be associated with a positive growth effect. It also does not preclude the possibility that within-sector risk sharing may be positively related to growth. The magnitude of the negative effect of risk sharing on growth revealed by the analysis is economically meaningful, indicating that investigation into the fundamental sources of differences in the extent to which returns on domestic assets covary with output movements across countries is warranted.
We know that
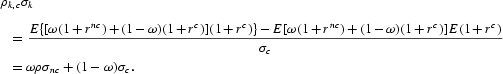
Differentiating with respect to ρ, we have
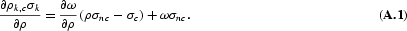
The sign of this derivative is determined by the sign of the expression
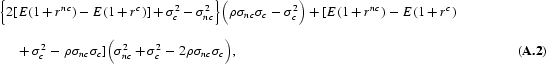
or
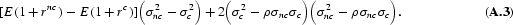
In what follows below, we also exploit the fact that the sign of ∂ω/∂ρ is determined by the sign of the expression
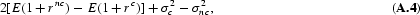
and the facts that
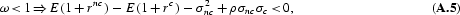
and
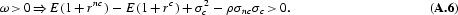
There are four cases to consider:

Unless otherwise noted, all averages cover the period 1976–1999 for use in the cross-sectional analysis, and the periods 1976–1979, 1980–1984, 1985–1989, 1990–1994, and 1995–1999 for use in the panel analysis.
I would like to thank seminar participants at the University of Illinois Urbana–Champaign, the Western Economic Association Conference, the Midwest Theory and International Conference, and the Midwest Macroeconomic Theory Conference. I especially thank Tom Krebs for valuable discussions and advice, as well as Francisco Cribari-Neto, Brad Humphreys, and two anonymous referees. Any errors are my own.

Summary statistics

Correlations: Independent and dependent variablesa

Correlations: Independent variables and instrumentsa

Capital stock growth and diversificationa

Output growth and diversificationa
