INTRODUCTION
This paper revisits the existence of deflationary bubbles and the terminal conditions that rule them out.1
By terminal conditions we mean restrictions that apply in the limit as time goes to infinity. These include transversality and “no-Ponzi-game” conditions.
The literature we are extending goes back to two seminal papers by Brock (1974, 1975). Brock analyzes a closed-economy model where households save and receive liquidity services from holding money. At the time his papers were written, the necessary conditions for household optimality in infinite-horizon models—even for the special case of bounded utility functions—were not widely known. Brock correctly stated that a necessary condition is that the consumer must be indifferent between permanently reducing his money holdings by one unit, and enjoying a one-period marginal increase in utility due to the increased consumption, and leaving his money holdings unchanged, and enjoying the discounted present value of the marginal utility of that unit of money forever. Brock's mathematical formulation of this idea is equivalent to an expression that looks like a transversality condition, but that is, in general, neither necessary or sufficient for household optimality, and this has resulted in confusion.
The mispecification of a terminal condition in decades-old papers would be of little consequence, except that the important results on deflationary bubbles in Brock (1974, 1975) and Obstfeld and Rogoff (1986) depend on the exact specification of the necessary and sufficient conditions for household optimality. As many developed economies have experienced deflation in recent years, the issue is now of relevance to both academics and policy makers. The continued mistreatment of transversality conditions in such recent and important textbooks as Azariadis (1993) and Obstfeld and Rogoff (1996) also deserves mention. In this paper we provide the correct specification of the transversality condition that, together with the Euler equation, is the necessary and sufficient condition for household optimality in Brock's model. We provide (for completeness) a proof that these conditions are sufficient for optimality, and using the technique in Kamihigashi's (2000) elegantly simple proof, we also provide a proof that, under certain assumptions, the transversality condition is necessary.
Consistent with the early papers, we assume that the money supply grows at a constant rate μ>1 (or falls, if μ< 1). Using the necessary and sufficient conditions for the representative household's optimization problem, we then provide the correct specification of when deflationary bubbles can and cannot occur. We demonstrate that deflationary bubbles cannot occur when money growth is strictly positive (μ>1). We show, however, that when the money supply is contracting, but at a lower rate than the discount factor (β<μ<1), deflationary bubbles can occur; indeed, any separable utility function satisfying the usual regularity conditions can produce a deflationary bubble. We show that if the money supply contracts at a rate greater than the discount factor (μ≤β), then deflationary bubbles cannot exist.
Confusion about the correct terminal conditions also exists in models with both money and bonds. Turnovsky (1997, p. 24) and Ljungqvist and Sargent (2000, p. 511) assert that the household faces two transversality conditions: one for the terminal stock of bonds and one for the terminal stock of money. Perhaps more common, however, is the claim that there is only one transversality condition on the sum of the terminal stocks of debt and money: this assertion is made by Woodford (2003, p. 70) and Obstfeld and Rogoff (1996, p. 534). In addition to the household transversality conditions, in a model with money and debt, both the household and the government face another terminal condition in the form of a restriction on their feasible sets (or specification of their intertemporal budget constraint), often referred to as a “no-Ponzi-game” condition.2
It is not uncommon for authors to make no distinction between these two types of restrictions.
We argue that the restriction on the households' and government's feasible sets is most appropriately a restriction on their terminal stocks of bonds. Given this assumption, we demonstrate that the household has a single transversality condition that, along with the Euler equations, is necessary and sufficient for optimality. This condition says that the inner product of the vector of state variables (money and bonds) and the vector of present discounted values of marginal returns from increases in current state variables remains nonpositive as time goes to infinity. Together with the no-Ponzi-game condition restricting the terminal stock of bonds, the single transversality condition is equivalent to two transversality conditions: one on money and one on bonds.
Using these two transversality conditions, we demonstrate that deflationary bubbles exist or fail to exist under the same circumstances as in the model with money only, and we show that deflationary bubbles are characterized by nominal interest rates tending to zero. Given the two transversality conditions, the deflationary bubbles accompanied by strictly positive money growth in Woodford (2003) and Benhabib et al. (2002a) cannot exist.
Section 2 of the paper contains the model with money only; Section 3 analyzes the existence of deflationary bubbles in the model of Section 2 and Section 4 extends the model of Section 2 to one with money and bonds. Section 5 is the conclusion.
THE MODEL WHEN MONEY IS THE ONLY FINANCIAL INSTRUMENT
The Households
The economy is inhabited by a representative household and its government. Each period, the household receives an exogenous endowment of the single perishable consumption good and pays a lump-sum tax. It consumes the good and saves non-interest-bearing money. The household receives liquidity services from its money holdings and has preferences defined over paths of consumption and holdings of real balances represented by
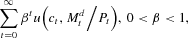
where ct≥0 is time-t consumption,
is the household's time-t demand for nominal money balances, Pt is the period-t money price of the good, and
.3
, and Z+={0, 1, 2, …}.
The household maximizes its utility subject to the sequence of within-period budget constraints
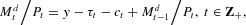
where y>0 is the constant per-period endowment and τt
is the period-t real lump-sum tax. Households take as given their initial money holdings
. We only consider outcomes where
for every t∈Z+. There is, however, always a nonmonetary equilibrium where 1/Pt=0 for every t∈Z+. In this outcome, money is not held and the household consumes its after-tax endowment each period.
DEFINITION 1. A sequence
is said to be feasible if it satisfies (2). A feasible sequence
is said to be optimal if
for every feasible sequence
We use the notational convention
We use the following assumptions:
Assumption 1.
- (i) u(c, m)>−∞ for
- (ii) u is C1 on , is concave, and has uc(c, m)>0 and um(c, m)≥0, for .
Assumption 2. There exist a constant ρ∈R and a summable sequence {bt} such that βt[uc(c, m)c+um(c, m)m]≤ρβtu(c, m)+bt, for every
A sequence {xt} is said to be summable if
Assumption 2 puts a limit on how fast utility can go to minus infinity when consumption or real balances go to zero. Suppose that u(c, m)=h(c)+v(m). If h(c)=ln(c) or c1−θ/(1−θ) and v(m)=ln(m) or m1−θ/(1−θ), θ>1, then Assumption 2 is satisfied. However, if h(c)=e−1/c or v(m)=e−1/m, then it is not satisfied. See Ekeland and Scheinkman (1986).
Assumption 3. uc(c, m)→∞ as c
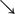
0; um(c, m)−uc(c, m)→∞ as m
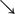
0.
Assumption 4. There exists
such that
Assumption 5. Either
- (i) um(c, m)>0 for and limm→∞um(c, m)=0 or
- (ii) for every c∈R++ there exists such that um(c, m)>(=) 0 if .
Not all of these assumptions are used for all of our results.
PROPOSITION 1.Assume that Assumption 1 holds. Sufficient conditions for the feasible sequence
where
, to be optimal are the Euler equation,
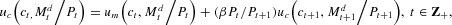
and the transversality condition,
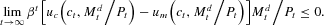
The proof of this proposition for similar problems is standard (see, for example, Brock (1974)). For completeness, a proof for this particular problem is provided in the Appendix.
Equation (3) is typical of the Euler equations that characterize investment in a consumer durable and has the following interpretation. The household is indifferent between a (small) one-unit increase in period-t consumption, which yields utility of
and foregoing this consumption and acquiring a one-unit increase in period-t real balances, which yield current utility of
and which can be traded next period for Pt/Pt+1 units of the consumption good, which yields a discounted utility of
The transversality condition in an infinite-horizon problem is often viewed as the analogue of the period-T complementary slackness condition in a T-period finite-horizon problem. This complementary slackness condition states that either
or
. If Assumption 3 (the Inada conditions at zero) holds, then
and households are willing to hold real balances only up to the point where the marginal utility gain from the current liquidity services of money equals the marginal utility loss from decreased current consumption. In our infinite-horizon problem, equation (4) implies that either the optimal value of the state variable,
goes to zero as time goes to infinity or its marginal contribution to the optimized value of the objective function,
becomes nonpositive.
That the transversality condition is a necessary condition in problems similar to this one was first proved by Weitzman (1973). His proof, however, requires the strong assumption that the utility function is bounded and does not cover common utility functions such as u(c)=ln(c) or c1−θ/(1−θ), θ>1, where u(c)→−∞ when c
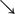
0. Ekeland and Scheinkman (1986) showed that under certain assumptions, the transversality condition is also necessary for unbounded utility functions. Kamihigashi (2000) relaxes some of Ekeland and Scheinkman's conditions and demonstrates that if utility does not go to minus infinity too quickly as consumption falls to zero and if the sequence of within-period discounted utilities is summable at an optimum, then the transversality condition must hold at that optimum.
PROPOSITION 2. Assume that Assumptions 1 and 2 hold. If the feasible sequence
where
is optimal and if
is summable, then
satisfies the transversality condition (4).
As the problem here is not identical to the one considered by Kamihigashi, a proof–which follows Kamihigashi's closely–is provided in the Appendix. Kamihigashi only requires that the set of points at which the utility function takes on a value strictly greater than minus infinity be an open set. Our stronger assumption that the utility function is strictly greater than negative infinity on
simplifies the proof.
The strategy of the proof is to compare an optimal sequence
with the following feasible perturbation: at time T, the household reduces its real balances to
and increases its consumption to
, 0<λ<1. Thereafter, its consumption and real balances are given by
Thus, optimality requires that utility with the optimal sequence be at least as great as utility with the perturbation, and this implies that
. If the right hand side of this inequality can be shown to go to zero as T→∞, then applying λ→1 to the left-hand side, using the definition of a derivative, and letting T→∞ establishes the result.
It is typical to consider models where Assumption 3 holds. In this case, the Euler equation (3) is also necessary and
A proof of this can be found in Brock (1974). Then, by (3) and (4), the transversality condition can be written as
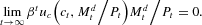
In the remainder of Section 2 and in Section 3, we assume that Assumptions 1–5 hold and we refer to equation (5) as the transversality condition.
The Government
The government's within-period budget constraint, assumed to hold with equality, is
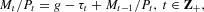
where g∈[0, y) is constant per-period public spending and Mt is the time-t money supply. We assume a constant proportional growth rate for the money stock:
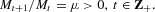
The sequence of lump-sum taxes is endogenously determined to make public spending and the growth rate of the money stock consistent with the sequence of within-period government budget constraints and τt<y+Mt−1/Pt; the assumption g<y ensures that this is always possible.
Equilibrium
In equilibrium,
and
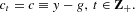
DEFINITION 2. Given {Mt}, an equilibrium is a sequence of prices {Pt} such that Pt∈R++, t∈Z+, and {c, Mt/Pt} is optimal for the household.
DEFINITION 3. If {Pt} is an equilibrium sequence of prices then {mt}, where mt≡Mt/Pt, t∈Z+, is an equilibrium sequence of real balances.
Substituting (8) and the money market clearing condition into (3) and (5) yields
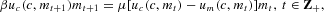
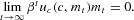
In what follows we will use the following:
DEFINITION 4. A sequence of real balances {mt} is said to satisfy the summability condition if {βtu(c, mt)} is summable.
Propositions 1 and 2 and Definitions 2–4 yield the following remark.
Remark 1. A sequence {mt}, mt>0, t∈Z+, satisfying (9) and (10) is an equilibrium sequence of real balances. If {mt} is an equilibrium sequence of real balances then it satisfies (9) and, if it satisfies the summability condition, then it satisfies (10).
There are two potential types of equilibria. First, given our constant fundamentals (y, g, μ), there is a fundamental (or Markov or “minimal-state-variable”) equilibrium where mt=m>0 for every t∈Z+. Constant real balances clearly satisfy (10). By (9), such an equilibrium has
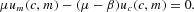
If μ<β or if μ=β and um(c, m)>0, m∈R++, then the left-hand side of equation (11) is strictly positive for every m∈R++ and no fundamental equilibrium exists. If μ=β and there is satiation in real balances, then any
satisfies equation (11), where
is as defined in Assumption 5(ii). Such an outcome is a Friedman (1969) optimal quantity of money (OQM) equilibrium, where the nominal stock of money declines proportionally at the rate of time preference and the household is satiated at a finite stock of real balances. If μ>β, then by Assumptions 3–5, μum(c, m)−(μ−β)uc(c, m)→∞ as m
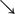
0 and μum(c, m)−(μ−β)uc(c, m)
as m→∞. Thus at least one fundamental equilibrium exists. For this case, the additional restriction that real balances are a normal good at any fixed point would ensure that the fundamental equilibrium is unique.
6If u is twice differentiable we can write this condition as ucumm−umucm<0 at a fixed point.
In addition to fundamental equilibria, there can be a variety of nonfundamental (or non-stationary) equilibria. [See Matsuyama (1991) and Azariadis (1993).' An equilibrium can be stable, with monotonic or cyclical convergence; it can be unstable, with either monotonic or cyclical divergence; there can be limit cycles and there can be chaotic behavior. We are interested in equilibria where real balances go to infinity; such equilibria are called deflationary bubbles.
DEFLATIONARY BUBBLES
In this section we consider the existence of deflationary bubbles.
The Definition of a Deflationary Bubble
Economists have many different definitions of bubbles, depending on the scenario under consideration. Here we have equilibria that depend solely on the fundamentals (and, hence, are not time-varying) and equilibria that depend on time as well as on the fundamentals. Of the equilibria that depend on time as well as on the fundamentals, we will define the ones that go to infinity over time to be deflationary bubbles. This is a standard definition; see, for example, Obstfeld and Rogoff (1986).
DEFINITION 5. A deflationary bubble is an equilibrium where mt→∞ as t→∞.
Note that this definition does not imply that an equilibrium sequence of prices that goes to zero must be a deflationary bubble or that all deflationary bubbles must have the price level going to zero. When the nominal money stock is falling, then a fundamental equilibrium has Pt+1/Pt=Mt+1/Mt=μ<1 and the price level goes to zero over time. When the nominal money stock is rising, a deflationary bubble has Pt+1/Pt = μmt/mt+1 and can be associated with rising prices if real balances are rising at a rate less than μ. Along such a path, however, inflation will be less than the associated fundamental equilibrium's inflation rate of μ.
Brock's Restriction on Optimal Programs
Writing before the publication of Weitzman's (1973) proof of the necessity of the transversality condition for bounded utility functions, Brock (1975, p. 140) proposed a necessary condition for optimal programs. He made a “no-arbitrage” argument that at an optimum, the household must be indifferent between permanently reducing its real balances by one unit today and enjoying a marginal increase in today's utility due to higher consumption and leaving its real balances unchanged and enjoying the discounted utility from the services of that unit of money forever. Brock expressed this condition mathematically as7
Brock assumed a separable utility function; this condition is the nonseparable analogue to his condition.
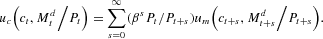
As shown in the previous section, there are two necessary conditions for household optimality. The first is the Euler equation, which relates time-t variables to time-(t+1) variables. The necessity of this condition is shown by switching small amounts of consumption and real balances between time t and time t+1 and then demonstrating that the first path yields at least as high utility as the second. The second is the transversality condition, which is a condition on the asymptotic behavior of consumption and real balances as time goes to infinity.8
See Ekeland and Scheinkman (1986) for a discussion of this.
Solving the Euler equation (3) forward yields
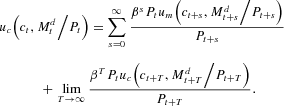
By equation (13), equation (12) is equivalent to
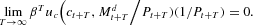
At an equilibrium, this can be written as
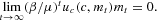
Thus, Brock's mathematical formulation of his “no-arbitrage” argument, when combined with the Euler equation, produces an equation that looks like a transversality condition, and this has apparently led to a substantial amount of confusion. Obstfeld and Rogoff (1983, p. 681; 1986, pp. 360–361), Gray (1984, p. 110), and—more recently—Azariadis (1993, pp. 403, 405) and Obstfeld and Rogoff (1996, pp. 541–542) all reproduce Brock's “no-arbitrage” argument and use it to claim that equation (14) is a transversality condition and necessary for household optimality.9
Gray (1984) notes that transversality conditions generally require the product of the state variable and its discounted value to go to zero as time goes to infinity, as in equation (4). In her paper and in Obstfeld and Rogoff (1986), the money stock is constant and hence equation (4) and equation (14) turn out to be the same. However, the technique they use to derive (14) would yield (4) if the money supply were not constant.
The proof of Proposition 2, demonstrating that transversality condition (4) is necessary for household optimality, employs Brock's proposed perturbation of current (that is, time-t) and future real balances and consumption. However, as seen in equation (A.3) in the Appendix (and also in the discussion following the statement of Proposition 2 in the text), the mathematical expression for this perturbation differs from Brock's, and is used only asymptotically, as time goes to infinity.
The GABOR condition has been used to study the theoretical existence of deflationary bubbles by Brock (1974, 1975) and Obstfeld and Rogoff (1986) in their well-known papers. In his Theorem 3 (p. 140), Brock (1975) assumes a separable utility function: u(c, m)=h(c)+v(m). He attempts to show that for μ>β no deflationary bubble can satisfy the GABOR condition. As this is not in general true, he imposes an additional condition: there exists a λ<0 such that for sufficiently large m, v′(m)<mλ. This condition is weak, if not particularly intuitive. Thus, if equilibria must satisfy the GABOR condition, then it is only in “pathological” cases that deflationary bubbles can exist. Obstfeld and Rogoff (1986) consider the case of μ>1 and show that under the stricter, but more intuitively appealing, condition that utility is bounded above in real balances, imposing the GABOR condition is sufficient to rule out deflationary bubbles.10
Obstfeld and Rogoff (1986) restrict attention to this case because they claim that Brock's proposed perturbation of an optimal sequence is not feasible otherwise. Equations (2) and (A.3) (in the Appendix) make it clear that the perturbation—as specified in (A.3)—is always feasible.
By (10) and (15) the transversality condition implies the GABOR condition when μ>1 and the GABOR condition implies the transversality condition when μ<1; the conditions are equivalent when μ=1. Thus, if μ>1 and a sequence {mt} satisfies the summability condition and has mt→∞ as t→∞, then using the GABOR condition to rule out this candidate deflationary bubble is legitimate: the transversality condition is necessary for household optimization (Proposition 2) and the GABOR condition is necessary for the transversality condition. But it makes more sense to use the stronger transversality condition. In the next section we present a simple proof ruling out deflationary bubbles that requires no additional assumptions.
If μ>1, mt→∞, and {mt} does not satisfy the summability condition, then neither the transversality condition nor the GABOR condition has been demonstrated to be necessary. Hence, they cannot be used to rule out deflationary bubbles.11
Suppose that u(c, m)=h(c)+v(m), where v(m)=m1−θ/(1−θ) if 1 ≠θ>0 and v(m)=ln(m) if θ=1. If {mt} satisfies (9) and mt→∞ as t→∞ then {mt} satisfies the summability condition if βθμ1−θ<1. Details on request.
When μ<1 it is not legitimate to use the GABOR condition to rule out deflationary bubbles satisfying (9) and (10). As the transversality condition is sufficient (Proposition 1), the stronger (in this case) GABOR condition cannot be necessary. In the next section we show that any sequence {mt} satisfying (9) and where mt→∞ also satisfies the transversality condition and is an equilibrium deflationary bubble.
The Relationship between the Transversality Condition and the “No-Bubble” Boundary Condition
Turning briefly to a different scenario, consider the market for a particular company's stock in a model without money in the utility function. Under certainty the household's Euler equation corresponding to that stock says that ptu′(ct)=β(pt+1 + dt+1)u′(ct+1), 0<β<1, where u is the within-period utility function and ct, pt, and dt are the time-t consumption demand, stock price (in terms of the consumption good), and (exogenous) dividend, respectively. Suppose that, as in our model, ct=c≡y−g, t∈Z+. Then solving the Euler equation forward would yield pt =
Thus, the stock price consists of a term
, which depends on the fundamentals (that is, the dividends), and a term Ct≡limT→∞βTpt+T.
This latter term may be strictly positive if investors have self-fulfilling expectations that the price will rise by more than is justified by the fundamentals. Alternatively, this term may be written as Ct=k/βt, where k ≥0. Solutions where k>0, and hence Ct≠0, are often referred to as rational or equilibrium bubbles. They might be viewed as unlikely or not “sensible,” as they are not Markov or “minimal-state-variable” solutions in McCallum's (1983) sense, because they depend on an extraneous variable: calendar time. In theoretical models it is typical to impose the boundary condtion limT→∞βTpt+T=0 to rule out such equilibria. In empirical models, deviations between pt and the fundamental component, Ft, are often referred to as bubbles and researchers often test for the existence of a bubble by testing whether the price can be explained by the fundamentals: in this example, this would be testing whether pt=Ft.
The boundary condition ruling out bubble equilibria looks like a transversality condition and some researchers, for example, Froot and Obstfeld (1991), call this condition a transversality condition. However, it is not related to the transversality condition that, under certain assumptions, is necessary and sufficient for household optimality. In the model of stock prices this transversality condtion would be limT→∞βTu′(cT)pTsT≤ 0, where st is the household's time-t holdings of the stock. In the model of this paper, when the Euler equation (3) is solved forward to find Brock's condition (13), it looks similar to the procedure where the equilibrium condition ptu′(ct)=β(pt+1+dt+1)u′(ct+1), ct=c, t∈Z+, is solved forward to find the stock price as the sum of a fundamental solution (Ft) and a bubble component (Ct) and the bubble component is then set equal to zero.
In our model, the analogous procedure for decomposing the general form for an equilibrium into fundamental and bubble components is not to solve the household's Euler equation forward, but to solve the equilibrium condition (9) forward. Equation (9) is not, in general, linear and this prevents a closed-form solution, but in this model with constant fundamentals, the analogue of Ft is the constant fundamental equilibrium
that solves (11). For the particular case of u(c, m)=h(c)+ln m, equation (9) is linear and can be solved forward to find
. Thus, for this special case, the GABOR condition can be used to rule out paths of real balances that are consistent with household optimization and market clearing, but that depend on a variable other than the fundamentals.
The Existence of Deflationary Bubbles
In this section we use the equilibrium conditions to characterize when deflationary bubbles can and cannot exist.
PROPOSITION 3. Suppose that a sequence {mt} has mt→∞ as t→∞.
- (i) If μ>1 and {mt} satisfies the summability condition, then {mt} is not an equilibrium sequence of real balances.
- (ii) If β<μ<1 and {mt} satisfies (9) then {mt} is an equilibrium sequence of real balances.
Proof. Suppose that μ>1 and let xt≡uc(c, mt)mt>0. By (9), xt+1/xt=(μ/β)[1−um(c, mt)/uc(c, mt)], t∈Z+. By Assumptions 3 and 4, xt+1/xt→μ/β as mt→∞. Thus, ∀ε>0, ∃T∈Z+ such that xT+t+1/xT+t>μ/β−ε,
Let ε=(μ−1)/β. Then βT+txT+t>βTxT>0, t∈Z++. Hence, βT+txT+t cannot go to zero as t→∞, and (10) is violated. This yields (i). If {mt} satisfies (9) then xt+1/xt≤μ/β, t∈Z+. Thus, βtxT+t≤μtxT→0 as t→∞, T∈Z+. Thus (10) is satisfied.
When β<μ<1 it is easy to find examples of deflationary bubble equilibria; indeed, any separable utility function u(c, m)=h(c)+v(m), where Assumptions 1–5 are satisfied, produces deflationary bubbles.12
When u is separable, (9) implies that dmt+1/dmt>mt+1/mt. Thus, dmt+1/dmt is strictly greater than one at any steady state.
When μ=1, the transversality condition and the GABOR condition are identical and Brock's and Obstfeld and Rogoff's results apply here. Obstfeld and Rogoff (1986) provide an example (suggested by Guillermo Calvo and Roque Fernandez) of a utility function where the GABOR condition (and hence the transversality condition) alone is insufficient to rule out deflationary bubbles. This utility function is separable and has the property that the marginal utility of money is 1/ln(m) for m large. If
, the sequence {mt} that satisfies equation (9) also satisfies the GABOR condition and has mt→∞.
We now consider the case of μ≤β. We show that when money growth equals the discount factor and there is satiation in real balances, deflationary bubbles cannot exist. When μ<β, fundamental equilibria do not exist. This case is not considered by Brock (1974, 1975). We show that there are no deflationary bubbles in this case either. Both results are a consequence of the Euler equation, rather than of the transversality condition.
PROPOSITION 4. Suppose that a sequence {mt} has mt→∞ as t→∞. If μ≤β, then {mt} cannot be an equilibrium sequence of real balances.
Proof. By (9),
, t ∈Z+. Thus, by Assumption 1,
, t∈Z+, and, hence,
. Thus,
When μ=β, Brock (1975) shows that if u(c, mt)=h(c)+v(m), where v′(m)>(<, =) 0 for m<(>, =) 0 and limm→∞v(m)=−a<0, a>0, then deflationary bubbles satisfy (9) and (10) if and only if a is sufficiently small.
In the final proposition in this section we demonstrate that using the GABOR condition rules out the OQM equilibrium.
PROPOSITION 5.The GABOR condition rules out Friedman's optimal quantity of money equilibrium.
Proof. Let μ=β and let
. Then (β/μ)tuc(c, mt)mt=uc(c, m′)m′>0 and the GABOR condition is not satisfied.
DEFLATIONARY BUBBLES WITH MONEY AND GOVERNMENT BONDS
In this section we extend the model to allow for government debt as well as money.
Households
We assume that the government issues nominal bonds, in addition to money.13
Including real bonds is trivial and adds to the notation without changing the results.
In the money-and-bonds model, too, we do not consider the nonmonetary equilibrium with
Denote the period-t household demand for bonds by
and let
The household's within-period budget constraint is
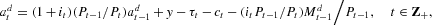
where it is the nominal interest rate between periods t−1 and t and
. We assume that the household's initial holdings of money and bonds, M−1>0 and B−1, respectively, are given.
The household cannot run a Ponzi scheme in which it borrows ever-increasing amounts to service its previously accumulated debt. We impose the restriction that the present discounted value of the household's terminal (nonmonetary) debt must be nonnegative:
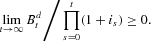
Many recent papers, however, contain an alternative restriction:
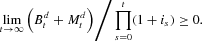
This no-Ponzi-game condition is an assumption about how the world works and therefore a matter of opinion. To see why we prefer (17), imagine an analogous T-period model, where T<∞. Typically, one would impose a restriction similar in spirit to (17): in the last period all previously accumulated debt must be repaid and no additional borrowing can take place. Suppose instead that one imposed a restriction similar to (18): outstanding debt need not be repaid if the household holds real balances equal to the outstanding debt. It is difficult to see why anyone would lend to the household when there is no future in which he or she would be repaid. In addition, if utility is strictly increasing in (end-of-period) real balances, households would want to hold an infinite amount of real balances and an infinite amount of debt in the last period and the household's optimization problem would have no solution.
Similarly, in an infinite-horizon model it is difficult to see why any counterparty would want the present discounted value of its terminal debt to be strictly positive. If it is argued that there is some unusual circumstance where a counterparty—say, the government—is willing to lend ever-increasing amounts to the private sector then using restriction (18) might be appropriate, but its use presents a problem. The conventional method of proving the sufficiency of the Euler and transversality conditions for household optimality requires the use of the stronger condition (17).15
This is seen in the proof of Proposition 6 in the Appendix.
DEFINITION 6. A sequence
is said to be feasible if (16) and (17) are satisfied. The definition of optimality is as in Definition 1.
PROPOSITION 6. Assume that Assumption 1 holds. Sufficient conditions for the feasible sequence
, where
to be optimal are that it satisfies the budget constraint (16), the Euler equations
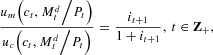
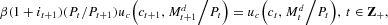
and the transversality condition.
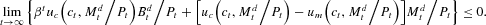
Proof. See the Appendix.
The transverality condition (21) appears unusual, but has the same interpretation as the transversality condition for the multisector growth model in Stokey and Lucas (1989): the inner product of the vector of state variables and the vector of present discounted values of marginal returns from increases in current state variables is nonpositive as time goes to infinity. Here the value of the marginal return of an increase in current bond holdings is the marginal utility loss due to foregone consumption; the value of a marginal increase in current money holdings is the marginal utility loss due to foregone consumption less the marginal utility gain due to increased liquidity services.
PROPOSITION 7. Assume that Assumptions 1 and 2 hold. If the feasible sequence
where
is optimal then it satisfies the transversality condition (21).
Proof. See the Appendix.
In the remainder of this section we assume that Assumptions 1–5 hold. In this case the Euler condition is necessary as well. By (17) and (20), the no-Ponzi-game condition can be rewritten as
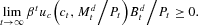
By (19) and nonnegative nominal interest rates,
. Thus,
and (21) and (22) together are equivalent to the pair of conditions
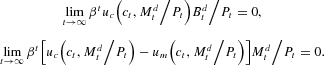
Substituting (19) into (23) implies that
. If the interest rate does not go to infinity (which by (19) and Assumption 3 would require an inflationary bubble), this condition can be expressed in the more familiar form
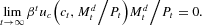
The Government
Let bt≡ Bt/Pt, where Bt−1 is the government's outstanding stock of bonds at the beginning of period t, and let at≡mt+bt. We restrict the government to rules satisfying at + y−g>0, t∈Z+, and assume that a−1 + y−g>0. The government's period-t budget constraint is
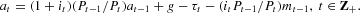
It is typical to express the government's long-run solvency constraint as
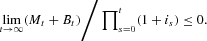
However, we assume that the money in the model is unbacked fiat money. Thus, as it is irredeemable, it is not a liability of the government (see Buiter (2003, 2005)) and the government's solvency constraint is
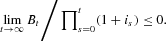
We view the government as choosing {Mt, Bt} such that, given prices and g, {Bt} satisfies (27).16
There exists a substantial empirical literature testing whether or not governments satisfy (27). Using U.S. data, Hamilton and Flavin (1986) and Trehan and Walsh (1988) find supportive evidence; Wilcox (1989), who uses U.S. data, and Smith and Zin (1991), who use Canadian data, find evidence that governments follow unsustainable policies, suggesting either that the government is playing a Ponzi game or that a change in policies is expected Of course if governments do not satisfy (27), then they do not satisfy the stronger condition (26).
Market Clearing
Market clearing requires that
and
As before, the resource constraint implies that ct=c≡y−g, t∈Z+. The assumption that at + y − g>0 ensures that it is always possible to find a sequence of taxes satisfying the assumed restriction
τt, t∈Z+. Thus, by equations (19), (20), and (23), we have the following definition:
DEFINITION 7 An equilibrium sequence of real balances is a sequence {mt} such that mt∈R++, t∈Z+, and
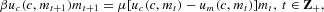
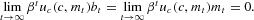
In an equilibrium, nominal interest rates are given by
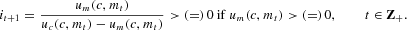
As before, a fundamental equilibrium exists when μ>β. By (28) and (30) it has the associated nominal interest rate
Deflationary Bubbles in a Model with Bonds
We demonstrate that adding government bonds to the model does not change the results of the previous section.
PROPOSITION 8. Suppose that {bt} satisfies (29) and that {mt} has mt→∞ as t→∞.
- (i) If μ>1 and {mt} satisfies the summability condition, then {mt} is not an equilibrium sequence of real balances.
- (ii) If β<μ<1 and {mt} satisfies (9), then {mt} is an equilibrium sequence of real balances and it+1→0.
- (iii) If μ≤β, then {mt} is not an equilibrium sequence of real balances.
Proof. The proof of Proposition 3 demonstrates that if {mt} satisfies (28) and has mt→∞ as t→∞, then {mt} satisfies (29) when β<μ<1 and fails to satisfy (29) when μ>1. This yields (i) and (ii). The proof of Proposition 4 demonstrates that if μ≤β then {mt} cannot satisfy (28). This yields (iii).
Our results are in contrast to the results in Woodford (2003, pp. 131–135) and Benhabib et al. (2002a, Sect. VI.A), who find that adding debt changes the regions of the parameter space where deflationary bubbles can exist. They use the alternative no-Ponzi-game condition (18). They then demonstrate that, when money is growing at a strictly positive rate, it is possible to have a sequence of real balances that tends to infinity and that satifies the Euler equations and this alternative no-Ponzi-game condition. This bubble has the property that, as the discounted present value of money balances goes to infinity, the present discounted value of government debt goes to minus infinity.
CONCLUSION
Terminal conditions have been problematic for monetary economists. Their specification differs from paper to paper and textbook to textbook, although the same model is employed. Restrictions on feasible sets (that is, the “no-Ponzi-game” conditions) are commonly not distinguished from the necessary and sufficient conditions for optimality, given the particular choice of a restriction on the feasible set. The intent of this paper is to provide a coherent treatment of the subject for two common models: a model with money in the utility function where money is the only financial asset and a model with money in the utility function and both money and bonds serving as financial assets.
We specify the necessary and sufficient conditions for household optimality, and we provide the relevant proofs. In the model with money only, we demonstrate that the transversality condition that is part of the necessary and sufficient conditions differs from a condition employed elsewhere in the literature. In the model with money and bonds we argue for particular restrictions on the household's and government's feasible sets. Using the restriction on the household's feasible set, we find the household transversality condition that, together with the Euler equation, constitutes the necessary and sufficient conditions for household optimality. Our result implies that in equilibrium there are a pair of terminal conditions that must be satisfied—one on money and one on bonds—rather than the single condition on the sum of the stock of money and bonds that frequently appears.
The resurgence of actual and prospective disinflation in industrialized countries has resulted in new interest in the possibility of self-fulfilling deflationary expectations. We use our results to demonstrate that, whether there is only money or there are money and bonds, deflationary bubbles cannot occur with reasonable utilty functions and positive nominal money growth. However, if the nominal money stock is falling, but not faster than the discount factor, then any sensible separable utility function can produce a deflationary bubble. If households have satiation in money balances, then a decline in money growth that supports Friedman's optimal quantity of money equilibrium (that is, a decline equal to the discount factor) cannot produce deflationary bubbles.
APPENDIX
Proof of Proposition 1. Let
be a feasible sequence. By (2),
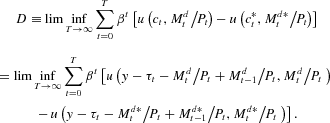
Then by Assumption 1,

Thus, by (3) and the given initial conditions,
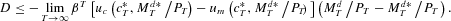
By (3) and Assumption 1,
; hence,
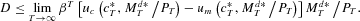
Equation (4) implies that the right-hand side is nonpositive, establishing the result.
Proof Proposition 2. The proof requires two lemmas.
LEMMA 1. If there exist a constant λ*∈(0, 1) and a summable sequence {et} such that
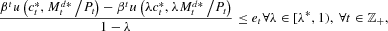
then the transversality condition (4) holds.
Proof. Suppose that there exist a λ*∈(0, 1) and a summable sequence {et} such that (A.2) holds. Let T∈Z+ and λ∈[λ*, 1), and define
by
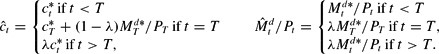
By (2),
is feasible. By the definition of optimality and (A.3),
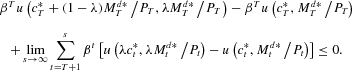
Therefore, by (A.2),
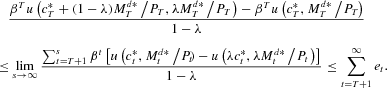
Let λ→1. By the definition of a derivative,
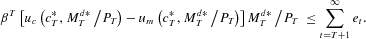
Letting T→∞ yields the result.
LEMMA 2. Let ρ∈R and let bt be as in Assumption 2. Then
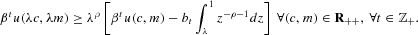
Proof. Let (c, m)∈R++ and t∈Z+. Define v(z)=βtu(zc, zm) for z∈(0, 1]. By the definition of v, ρ, and bt,
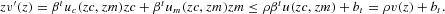
This implies, that
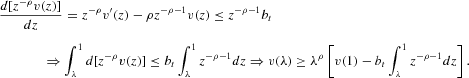
By the definition of v, this yields the result.
To prove Proposition 2, let λ*∈(0, 1), λ∈[λ*, 1), and t∈Z+. By Lemma 2,
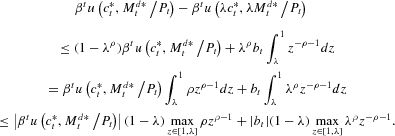
Thus,
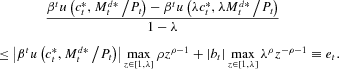
The sequence {et} is summable; hence, by Lemma 1, the proposition is proved.
Proof of Proposition 6. Let
be any feasible sequence. By (16),

Then by Assumption 1,
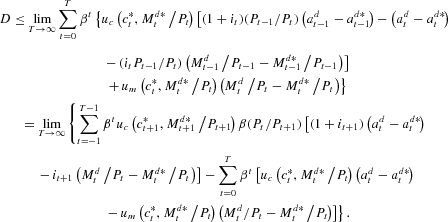
Thus by (19), (20), and the initial conditions,
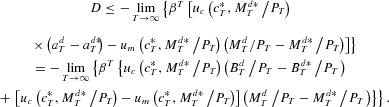
By (19), when it+1=0,
, and when it+1>0,
; hence
By (17) and (20),
Thus
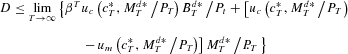
The right-hand side is nonnegative by (21), establishing the result.
Proof of Proposition 7. Except for Lemma 1 this follows the proof of Proposition 2 in a straightforward manner. In the statement of Lemma 1, (4) is replaced by (21). The proof of Lemma 1 is now as follows.
Suppose that there exist a λ*∈(0, 1) and a summable sequence {et} such that (A.2) holds. Let T∈Z+ and λ∈[λ*, 1), and define
by
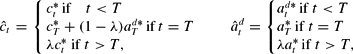
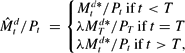
By (16),
is feasible. By the definition of optimality and (A.3),
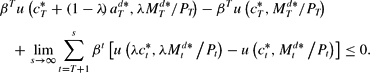
Therefore, by (A.2),
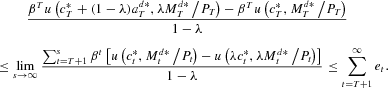
Let λ→1. By the definition of a derivative,
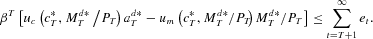
Letting T→∞ yields that the left-hand-side is nonpositive; feasibility ensures that it equals zero.
We would like to thank William Brock, Jo Anna Gray, and Narayana Kocherlakota for useful comments.


