1. INTRODUCTION
The phenomenon of mirage (Knowlton, Reference Knowlton1919; Raman & Pancharatnam, Reference Raman and Pancharatnam1959; Vollmer, Reference Volllmer2009) is beautiful, sometimes mysterious, but it is not observed very often. The mirage originates from uncontrolled deflection of light rays from their refractive propagation in inhomogeneous medium. Upper part of Figure 1 illustrates the physical mechanism of the appearance of an optical mirage in an ocean when light rays propagate through an inhomogeneously heated air near the ocean surface. As can be seen from Figure 1, a sort of optical system (eyes or photo camera) is needed for the observation of visible mirage. The phenomenon of the mirage has been associated with visible light and during more than 100 years after Roentgen discovery, the mirage was not observed in X-ray energy range. Indeed, the appearance of a mirage in the X-ray is extremely difficult because of the low values of the refractive indices of media in the X-ray frequencies. The specific property of the X-ray optics is that the refractive index of all materials is close to 1. Obviously, the latter circumstance practically eliminates the formation of mirages in the X-ray range using conventional materials. In such case only advent of plasma media X-ray lasers (Elton, Reference Elton1990; Ceglio, Reference Ceglio1991; Pert, Reference Pert1994; Avrorin et al., Reference Avrorin, Lykov, Loboda and Politov1997; Daido, Reference Daido2002; Tallents et al., Reference Tallents, Abou-Ali, Edwards, King, Pert, Pestehe, Strati, Lewis, Keenan, Topping, Klisnick, Guilbaud, Ros, Clarke, Notley and Neely2002; Jaegle, Reference Jaegle2006; Suckewer & Jaegle, Reference Suckewer and Jaegle2009) and particular developing two -stage or seeded plasma-based X-ray transient collisional lasers (Baer et al., Reference Baer, Schwob, Eliezer, Henis and Eliezer1996; Le Pape & Zeitoun, Reference Le Pape and Zeitoun2001; Zeitoun et al., Reference Zeitoun, Faivre, Sebban, Mocek, Hallou, Fajardo, Aubert, Balcou, Burgy, Douillet, Kazamias, De Lachèze-Murel, Lefrou, Le Pape, Mercère, Merdji, Morlens, Rousseau and Valentin2004; Nishikino et al., Reference Nishikino, Hasegawa, Kawachi, Yamatani, Sukegawa and Nagashima2008, Reference Nishikino, Ochi, Hasegawa, Kawach, Yamatani, Ohba, Kaihori and Nagashima2009; Wang et al., Reference Wang, Granados, Pedaci, Alessi, Luther, Berrill and Rocca2008, Reference Wang, Wang, Oliva, Li, Berrill, Yin, Nejdl, Luther, Proux, Le, Dunn, Ros, Zeitoun and Rocca2014; Zimmer et al., Reference Zimmer, Zielbauer, Pittman, Guilbaud, Habib, Kazamias, Ros, Bagnoud and Kühl2010; Ecker et al., Reference Ecker, Oliva, Aurand, Hochhaus, Neumayer, Zhao, Zielbauer, Cassou, Daboussi, Guilbaud, Kazamias, Le, Ros, Zeitoun and Kühl2012; Oliva et al., Reference Oliva, Fajardo, Li, Pittman, Le, Gautier, Lambert, Velarde, Ros, Sebban and Zeitoun2012; Depresseux et al., Reference Depresseux, Oliva, Gautier, Tissandier, Nejdl, Kozlova, Maynard, Goddet, Tafzi, Lifschitz, Kim, Jacquemot, Malka, Ta Phuoc, Thaury, Rousseau, Iaquaniello, Lefrou, Flacco, Vodungbo, Lambert, Rousse, Zeitoun and Sebban2015) allowed to provide systematical investigations of plasma media optical properties and recently find plasma conditions for observing mirages in the X-ray region (Magnitskiy et al., Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013; Pikuz et al., Reference Pikuz, Faenov, Magnitskiy, Nagorskiy, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kato and Kawachi2014).
Fig. 1. Registration of optical mirages near the sea surface (a) and X-ray mirage in two-stage X-ray laser experiments with inhomogeneous plasma (b).
In this paper, we give the overview of our recent discovery of X-ray coherent mirage phenomenon. New experimental results and more detailed consideration about generation of phase – matched coherent point sources in plasma media by propagated X-ray laser seeded beam are presented. Coherent X-ray mirage phenomenon possible applications are discussed.
2. EXPERIMENTAL SET UP AND RESULTS
The general schemes of usual optical and X-ray mirage observations are presented in Figure 1 and they clearly demonstrate the main difference of visible and X-ray mirages methods of registrations. Indeed Figure 1a shows that optical mirage can be observed on the detector only by using optical imaging system such as a camera objective or an eye lens and cannot be detected directly by charge-coupled device (CCD) camera. Coherent X-ray mirage can be observed by using both optical system or by direct registration on X-ray detector, for example, on X-ray CCD camera (see Fig. 1b). Additionally, it is necessary to underline, that the principal difference of observed X-ray mirage compared with traditional mirages in optical range is the fact that X-ray mirage is coherent due to the phase-matching of real and imagingary sources, that is, their coherency. As can be seen from Figure 1b the observed coherent X-ray mirage has appeared in the form of interference pattern in spatial profile of the output of the two-stage transient-collisional plasma X-ray laser beam.
Coherent X-ray mirage has been discovered (Magnitskiy et al., Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013) during the series of experiments aimed at studying the spatial characteristics of the wave front of the output beam of the two-stage X-ray laser, where the laser-induced plasma is used as an active medium. The experiment with the soft X-ray laser (SXRL) facility has been performed (Nishikino et al., Reference Nishikino, Hasegawa, Kawachi, Yamatani, Sukegawa and Nagashima2008, Reference Nishikino, Ochi, Hasegawa, Kawach, Yamatani, Ohba, Kaihori and Nagashima2009) at Kansai Photon Science Institute of Japan Atomic Energy Agency. The spatially coherent SXRL pulse was generated with the silver plasma media using the oscillator-amplifier configuration, in the arrangement shown schematically in Figure 2. Thin Ag foils for the oscillator and the amplifiers were pumped respectively with the line-focused travelling wave laser pulses with the proper timing for the effective amplification. A part of the soft X-ray laser beam from the oscillator was amplified in the plasma of the X-ray laser amplifier. The amplifier target is slightly tilted with respect to the oscillator target since the X-ray laser beam is refracted in the plasma due to the plasma density gradient. The SXRL pulse after the amplifier had a wavelength of 13.9 nm, bandwidth of narrower than 10−4, pulse duration of 7 ps, and a beam divergence of 1.2 mrad (H) × 0.4 mrad (V). The SXRL system worked at 0.1 Hz repetition regime with the output energy of the order of 300 nJ. Spatial intensity distribution of an output X-ray beam has been measured in three different experiments, in which distances between X-ray detector and X-ray laser beam source varied from 1300 mm up to 6300 mm (see Fig. 3). Two types of X-ray detectors were used in experiments. In the first case the LiF crystal, which allowed to obtained images with submicron spatial resolution, was used to demonstrate shot-to-shot high reproducibility of X-ray mirage emerging. As it is clearly seen in Figure 3a even after 30 consecutive shots the contrast of interference pattern formed by the X-ray mirage effect is enough to resolve X-ray beam intensity modulations in fringes. In two other experiments, the X-ray laser beam profiles were recorded by a back illuminated X-ray CCD with 2048 × 2048 pixels and 13.5 µm-pxl-size. The spatial resolution of such detector is worse compared with LiF crystal detector, but the sensitivity is higher. This allowed us to measure the coherent X-ray mirage patterns in single laser shot at large distances from the laser plasma source and, undoubtedly, to investigate the changes of periods between interference fringes away from the SXRL output and compare them with modeling. Bright elongated spots (see Fig. 3b, 3c) obtained by X-ray CCD in the horizontal direction of the images represent the radiation, amplified in the second laser produced plasma. The enlarged images with intensity distributions of X-ray laser beam at the distance 3314 mm from the output of two regions of the beam are shown in the insets in Figure 3b. The ring structure is clearly observed in the spatial distribution, which covers almost the entire beam profile. Such ring structure of the interference fringes even more obviously seen in the images obtained at the distance 6300 mm from the output of X-ray beam (see images and trace in Fig. 3c). The ring structures obtained in our experiments were recorded consistently from shot to shot, which again confirms a high stability of X-ray coherent mirage (see Fig. 4) appearing under stable conditions of plasma parameters used for generation and amplification of XRL radiation. It is necessary to underline that the period of the fringes is gradually decreasing from the center to periphery and the explanation of such behavior is presented below in the discussion part.
Fig. 2. Scheme of two-stage X-ray transient collisional laser and main results demonstrated the high level of coherence and low angle of divergence (Nishikino et al., Reference Nishikino, Hasegawa, Kawachi, Yamatani, Sukegawa and Nagashima2008, Reference Nishikino, Ochi, Hasegawa, Kawach, Yamatani, Ohba, Kaihori and Nagashima2009).
Fig. 3. Experimental schemes of coherent X-ray mirage observations in two-stage X-ray transient collisional plasma laser experiments and the main results, which demonstrated (a) high reproducibility of interference patterns generation (accumulation by 30 laser shots does not smooth the contrast of observed fringes) and the possibility of propagation of X-ray beam carried interference patterns at large distances 3314 mm (b) and 6300 mm (c).
Fig. 4. Demonstration of shot to shot high reproducibility of X-ray mirage interference fringes emerging in output of SXRL at large distance of 6300 mm.
We would like to stress that the interference fringes were observed only in the case of two-stage laser generation scheme that is, when the generator and amplifier were turned on simultaneously (see Fig. 5). Additionally it was experimentally found that the ring structure exists for the relative delay of ≤10 ps between the two pump pulses of the oscillator and the amplifier, and only when the oscillator-amplifier target angle was of ≤0.6°.
Fig. 5. Experimental confirmation of the fact that interference pattern is formed only in the case when both generator and amplifier are in operation (bottom case). The distance second SXRL plasma medium – X-ray CCD = 3314 mm.
3. DISCUSSIONS
The presence of the interference fringes in the form of the concentric rings, allows us to suggest that these rings are produced by an interference of radiation emitted by two coherent sources, the sizes of which should be close to the point source sizes, and located on the line, passing through the center of the ring fringe structure. According to Born and Wolf (Reference Born and Wolf1980) a distance between sources defines the radius and period of fringes in plane of the detector. Indeed, as it can be seen from the sketch of interference fringes formation presented in Figure 6 concentric fringes with varying curvature can be obtained only by using 2-point sources separated by some distance. In our experimental case the origin of the first source is clear. This is the radiation, which is emitted from the oscillator and, hence, the corresponding point source is located somewhere in the vicinity of its input edge. Position of the second source is generally obvious. It should be located somewhere in the X-ray amplifier and can be evaluated using the period of interference pattern. As it was determined in Magnitskiy et al. (Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013) by matching the experimentally observed periods of interference patterns and the calculated ones, the distances between both sources in our experiments was 203 ± 2 mm. The distance between centers of the oscillator and the amplifier plasmas in our experimental set-up was 206 mm. It means that the second virtual point source (mirage source) is situated near the middle of the amplifier plasma. This result not only confirms the hypothesis of the birth of a mirage in the form of the X-ray point source, but also shows the excellent coherence properties of both sources. We would like to mention that appearance of the interference patterns in the form of the concentric rings in the spatial profile of the output X-ray laser beams is unique phenomenon and was never been observed previously when standard, one stage X-ray lasers, were used.
Fig. 6. Optical scheme of interference pattern formation by 2-point coherent sources. Modeling shows that along the axis of 2-point sources, period of fringes gradually decreased from central portion of interference pattern to periphery fraction. Crop parts of experimental images, registered at the distance 3314 mm from SXRL output, are the X-ray mirage images obtained at different distances from the center of interference. Good agreement between experimental and modeling results in the period of interference fringes behavior is clearly seen.
Only the advent of a two-stage X-ray lasers, allowed for the first time (Magnitskiy et al., Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013; Pikuz et al., Reference Pikuz, Faenov, Magnitskiy, Nagorskiy, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kato and Kawachi2014) to observe such effect. It is necessary to stress that, nothing like this has previously been observed also in the visible range, when laser radiation is amplified in the laser amplifier modules. As it was demonstrated in Magnitskiy et al. (Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013) the observed phenomenon cannot be explained with the standard Maxwell–Bloch equations (Larroche et al., Reference Larroche, Ros, Klisnick, Sureau, Moller and Guennou2000; Kim et al., Reference Kim, Jamulewicz and Lee2011). Indeed, in Maxwell–Bloch approach it is considered that the set of identical particles homogeneously dispersed in space. In such case the phase front of the stimulated emission must repeat the initial phase front and, therefore, cannot create a spherical wave with a phase front of another curvature, which is required for appearance of X-ray mirage. Additionally in Magnitskiy et al. (Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013) it was shown that a mirage formation cannot not be described taking into account the nonlinearity of the absorption process.
However Magnitskiy et al. (Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013) found a new approach for the explanation of the X-ray mirage phenomenon. As noted above, the laser-induced plasma in X-ray spectral range has unique electrodynamics properties. It was suggested that due to its high density and strong localization in space (see Fig. 7a, 7c) such plasma may provide conditions for emerging of X-ray mirage analogous to the formation of optical mirages, which are observed in the sea surfaces (Fig. 1). The possible mechanism leading to the formation of the X-ray mirage was explained by applying the effective inhomogeneous lens, simulating the X-ray optical properties of the plasma, with the larger thickness, which corresponds to lower refractive index. In the presence of amplification the central part of the beam will be amplified stronger. Since the surface of the equivalent lens near its extremes can be approximated by a parabolic surface, the central part of the plasma will work as an ideal aberration-free lens. Therefore, the higher the gain, the narrower axial region of the plasma will contribute to the amplified beam and, consequently, the produced virtual source will be closer to a point source.
Fig. 7. (a) Typical 1D spatial electron density profile of plasma in second X-ray laser media calculated in (Ohnishi et al., Reference Ohnishi, Nishikino and Sasaki2006), (b) gain profile distribution G(x, y), which was used for plasma modeling of X-ray mirage in (Magnitskiy et al., Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013), (c) spatial profiles of the electron density N e(x, y), which were calculated in (Berrill et al., Reference Berrill, Alessi, Wang, Domingue, Martz, Luther, Liu and Rocca2010) and used in for X-ray mirage modeling, (d) output energy of the amplified seeded beam versus the amplifier medium length: Results of numerical simulation are shown as the solid curve and the dark circles present the experimentally measured output energy of SXRL amplifier (Nishikino et al., Reference Nishikino, Hasegawa, Kawachi, Yamatani, Sukegawa and Nagashima2008).
Let us suppose that the wide divergent X-ray beam incidents on a small piece of plasma medium. Several factors will influence the formation of a mirage. First of all the spatial distribution of the refractive index, and also a gain of the medium will play a significant role in the process. Besides, since in typical X-ray lasers the gain coefficient is very high, it is necessary to consider the effect of saturation in signal amplification. It means that when an external beam passes through such optical system from the left hand side, it will consist of a set of outgoing waves generated by virtual point or extended sources located along the axis of symmetry (see Fig. 8c). As it was proposed by Magnitskiy et al. (Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013) and can be seen from Figure 8a it is possible to consider that the amplitude of X-ray field output
$A({\bi \vec r})$
consists of two terms: Amplitude of an incident beam propagating in empty space
${A_{{\rm inc}}}({\bi \vec r})$
and amplitude of the mirage radiation emerging in the plasma
${A_{\rm M}}({\bi \vec r})$
. So, it means that the term X-ray mirage was used in the same sense as it is understood in the optical range. Mathematically, this is a part of the total radiation that remains after subtracting from it the initial radiation under the assumption that the initial radiation propagates through a medium without distortion due to inhomogeneity of a medium.
Fig. 8. Schematical consideration of X-ray mirage stages formation.
According to schematical consideration presented in Figure 8a, 8b the incident seeded beam from generator that is, beam of our real SXRL source after propagation through the plasma of amplifier, is distorted by refraction. In the exit of the amplifier the output X-ray field has a complex amplitude
$A(\vec r)$
. If from the output SXRL field
$A(\vec r)$
to subtract the field of incident SXRL beam
${A_{{\rm inc}}}(\vec r)$
, which is propagating in empty space, the remaining part of the X-ray field
${A_{\rm M}}(\vec r)$
will describe an emerging X-ray mirage. In Magnitskiy et al. (Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013) to determine what imaginary source corresponds to the output mirage field, as well as to determine position of the source and field profile, the back run modeling of the output radiation through the space of amplifier without plasma has been done.
Above-mentioned consideration of the imaginary source emergence was used for a numerical three-dimensional (3D) simulation of passing the X-ray beam field through the plasma-amplifier media. It was supposed that the broad divergent Gaussian SXRL beam incidents on a small plasma clot, causes a distortion of the beam. The standard wave equation, which in the approximation of slowly varying amplitudes
$A(\vec r)$
can be written as
$$\eqalign{& \displaystyle{{\partial A(\vec r)} \over {\partial z}} = \displaystyle{1 \over {2ik}}{\Delta _ \bot} A(\vec r) + \displaystyle{k \over {2i}}[{\rm \varepsilon} (\vec r) - 1]A(\vec r),\;\cr &\vec r \equiv \{ x,y,z\},} $$
where
${\rm \varepsilon} (\vec r)$
is the permittivity of the plasma, the imaginary part of which models the amplification. The amplitude
$A(\vec r)$
was represented as the sum of two terms
$A(\vec r) = {A_{{\rm inc}}}(\vec r) + {A_{\rm M}}(\vec r)$
is the amplitude of a Gaussian beam propagating in empty space:
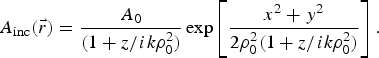$${A_{{\rm inc}}}(\vec r) = \displaystyle{{{A_0}} \over {(1 + z/ik{\rm \rho} _0^2 )}}\exp \left[ {\displaystyle{{{x^2} + {y^2}} \over {2{\rm \rho} _0^2 (1 + z/ik{\rm \rho} _0^2 )}}} \right].$$
It is possible to show that
${A_{\rm M}}(\vec r)$
is the amplitude of the radiation emerging in the plasma. It is not difficult to see that
${A_{\rm M}}(\vec r)$
satisfies the equation:
$$\displaylines{\displaystyle{{\partial {A_{\rm M}}(\vec r)} \over {\partial z}} = \displaystyle{1 \over {2ik}}{\Delta _ \bot} {A_{\rm M}}(\vec r) \cr + \displaystyle{k \over {2i}}[{\rm \varepsilon} (\vec r) - 1]({A_{\rm M}}(\vec r) + {A_{{\rm inc}}}(\vec r)),} $$
which can be regarded as an equation for the complex amplitude of X-ray mirage.
For modeling of the experimental results (Magnitskiy et al., Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013) the plasma was used as a 6-mm-length cylinder with a diameter of 50 µm, having 2D Gaussian density profile and the total gain coefficient g = 15 cm−1 in the maximum as can be seen from Figure 7b. The results of the numerical simulation of Eq. (1) are presented in Figure 9. The appearance of virtual X-ray sources in the plasma-amplifier is presented in Figure 9a. The position and the size obtained by modeling is in good coincidence with experimental results. It is necessary to underline that modeling showed that in the absence of amplification the additional radiation emerging in the plasma has a structure, which does not correspond to point source. And only incorporation in modeling the gain increase, allows to obtain an almost perfect laser beam with a spatial profile close to the Gaussian (Fig. 9b). One can also see that results of angular distribution of the output X-ray beam modeling (Fig. 9c) are in a very good agreement with the experimentally observed results (see Figs 3–5). Additionally, modeling demonstrates that it is possible to achieve good consistency between the calculated and experimental energy characteristics of our X-ray amplifier as it can be seen from Figure 7d.
Fig. 9. Simulations (Magnitskiy et al., Reference Magnitskiy, Nagorskiy, Faenov, Pikuz, Tanaka, Ishino, Nishikino, Fukuda, Kando, Kawachi and Kato2013) of different characteristics of the X-ray mirage. (a) Intensity distribution of X-ray mirage radiation in the vicinity of its imaginary waist. (b) Intensity distribution of X-ray mirage radiation at the output of the amplifier. (c) Angular spectrum of the output X-ray radiation.
All modeling provided allowed to formulate four main conditions, which should be satisfied for the generation of X-ray mirage:
-
(1) A local maximum in the electron density N e (x; y) distribution should exist
-
(2) Spatial location of the gain G(x; y) region should coincide with the position of the local maximum of electron density N e(x; y)
-
(3) Spatial size of a gain region should be equal or less than the width of the N e (x; y) of local maximum
-
(4) Uniformity of the plasma parameters distribution along the direction of X-ray beam propagation should be sufficiently high.
It is necessary to underline that the conditions (1) and (2) of the mirage formation are rather unique and do not always exist in the laser produced plasma, which are used as SXRL media. As can be seen from modeled results presented in Figure 7a, 7c such conditions are realized only at a certain stage of laser produced plasma temporal evolution. Such conclusion is well confirmed by our experimental results, which demonstrated that the X-ray mirage disappeared when the delay between the pumping laser pulses, which initiated the plasma generator and the plasma amplifier, exceeded 10 ps. Another important experimental discovery that is, disappearance of the X-ray mirage emergence at angles >0.6°, can be connected with breach of the condition (4).
4. CONCLUSION
It was demonstrated that, in plasmas produced by two laser beams, the generation of phase-matched coherent point source in amplifying plasma media by propagated X-ray laser seeded beam is possible. In the first plasma medium, which is the generator of SXRL beam, and in the second one, which is the amplifier for such beam, the real and imaginary sources are created, which can be associated with formation of mirage. The difference to visible mirage consists in coherency of X-ray sources of mirage formation and their ability to interfere. The necessary and sufficient conditions for observation of X-ray mirage have been formulated. It was demonstrated that plasma of laser amplifier can modify the X-ray laser wave front in the needed direction, and that it behaves as X-ray plasma optics. Moreover, the measuring of the interference patterns themselves could be an effective method of diagnostics of X-ray laser plasma media, including the coherence degree of output radiation of such lasers. The X-ray mirage phenomenon will be useful for further development of modern X-ray science and technology: for generation of adaptively controlled X-ray beams; for the further development of multistage X-ray lasers based on laser-induced plasmas; and for stable generation of interference fringes without any additional optical elements, which will open new way for X-ray interferometry and holographic studies. Also, plasma X-ray optics can find other different practical and scientific applications.
ACKNOWLEDGMENTS
This work is partly supported by JSPS Grant-in-Aid for Scientific Research Kiban (B) No. 25289244, partly supported by Russian Foundation for Basics Research (grant # 14-22-02089) and by RAS Presidium Program for basic research #11.
