1. INTRODUCTION
Interaction of high power laser fields with ionized plasma can be utilized for a number of applications including laser-induced fusion (Deutsch et al., Reference Deutsch, Furukaw, Mima, Murakami and Nishihara1996; Hora, Reference Hora2004), high-harmonic generation (Abdelli et al., Reference Abdelli, Khalfaoui, Kerdja and Ghobrini1992; Nuzzo et al., Reference Nuzzo, Zarcone, Ferrante and Basile2000; Salih et al., Reference Salih, Sharma and Rafat2004; Jha et al., Reference Jha, Mishra, Raj and Upadhyay2004), laser-plasma channeling (Sullivan et al., Reference Sullivan, Hamster, Gordon, Falcone and Nathel1994; Monot et al., Reference Monot, Auguste, Gibbon, Jakober, Mainfray, Dulieu, Jaquet, Malka and Miquel1995), and laser-plasma acceleration (Faure et al., Reference Faure, Rechatin, Norlin, Lifschitz, Glinec and Malka2006; Esirkepov et al., Reference Esirkepov, Bulanov, Yamagiwa and Tajima2006). For charged particles to reach high energies, electric fields must act on them over extended distances. Tajima and Dawson (Reference Tajima and Dawson1979), on the basis of theoretical work, showed that relativistic plasma waves are suitable for the development of compact accelerators. In their scheme, external electrons were accelerated through very high acceleration gradients sustained by relativistic plasma waves driven by laser pulses. Laser-plasma accelerators, which have been proposed as compact next-generation accelerators, rely on laser excitation of large amplitude plasma waves (with 10–100 GV/m field gradients) for trapping and acceleration of particles. Surfing the generated plasma wave, an externally injected test electron can experience much higher accelerating gradients than a conventional radio frequency linac could provide. A number of schemes have been proposed for the generation of large amplitude plasma waves and development of laser-plasma based accelerators that includes plasma beat wave accelerator (PBWA) (Dyson & Dangor, Reference Dyson and Dangor1991; Tochitsky et al., Reference Tochitsky, Narang, Filip, Musumeci, Clayton, Yoder, Marsh, Rosenzweig, Pellegrini and Joshi2004), plasma wakefield accelerator (PWFA) (Chen et al., Reference Chen, Dawson, Huff and Katlouseas1985), self-modulated laser wakefield accelerator (SMLWFA) (Ting et al., Reference Ting, Moore, Krushelnick, Manka, Esarey, Sprangle, Hubbard, Burris and Baine1997; Schroeder et al., Reference Schroeder, Esarey, Geddes, Toth, Shadwick, Tilborg, Faure and Leemans2003), and laser wakefield accelerator (LWFA) (Faure et al., Reference Faure, Rechatin, Norlin, Lifschitz, Glinec and Malka2006; Jha et al., Reference Jha, Saroch, Mishra and Upadhyay2012).
It is observed that the amplitude of the generated wakefields depends on the shape of an ultrashort, intense laser pulse. Interaction of highly relativistic short laser pulses with plasma and nonlinear wakefield generation by the laser pulses with realistic shapes has been studied by Berezhiani et al. (Reference Berezhiani and Murusidze1992). Effect of temporal pulse shapes on the laser excitation of plasma waves has been studied theoretically (Irani et al., 2012) as well as by two-dimensional (2D) particle-in-cell (PIC) simulation (Zhang et al., Reference Zhang, Shen, Ji, Wang, Xu, Yu, Yi, Wang, Hafz and Kulagin2012). Dependence of quasi-static wakefield and high harmonic generation on the pulse shape of an ultrashort, few-cycle laser has been shown by Malav et al. (Reference Malav, Maheshwari and Choyal2011). The effect of asymmetric laser pulse shapes on laser wakefield accelerators (Leemans et al., Reference Leemans, Catravas, Esarey, Geddes, Toth, Trines, Schroeder, Shadwick, Tilborg and Faure2002) have been reported. Zeng et al. (Reference Zeng, Shen, Yu and Xu1996) have theoretically predicted the dependence of relativistic harmonic radiation on the pulse shape of pumping laser. Considering super-Gaussian beam profile, THz radiation generation (Malik & Malik, Reference Malik and Malik2012) as well as laser wakefield acceleration (Ostermayr et al., Reference Ostermayr, Petrovics, Iqbal, Klier, Ruhl, Nakajima, Deng, Zhang, Shen, Liu, Li, Xu and Tajima2012) has been shown recently. In the field of laser-matter interaction, super-Gaussian pulses have extensively been used for investigating optical pulse transmission in fibers (Agrawal et al., Reference Agrawal and Potasek1986). Berezhiani et al. (Reference Berezhiani, Garuchava, Mikeladze, Sigua, Tsintsadze, Mahajan, Kishimoto and Nishikawa2005) have studied the interaction of relavistically strong super-Gaussian laser pulses with overdense plasma. In a recent study, Balakin et al. (Reference Balakin, Litvak, Mironov and Skobelev2012) have shown that the compression of the laser pulse with super-Gaussian profile is stronger than that of the triangular pulse. However, the interaction of super-Gaussian laser pulses with plasma is still a new field and requires a lot of attention for studying various physical phenomena occurring during interaction. Such effects have motivated the present study of wakefield generation by super-Gaussian pulses propagating in plasma.
In the present analysis, the excitation of longitudinal, electrostatic wakefields produced by a linearly polarized super-Gaussian laser pulse propagating through uniform plasma has been studied using 2D PIC simulations. The study proceeds by considering plasma to be cold and underdense. In order to validate the results obtained via simulations, we have studied the generation of wakefields by one-dimensional (1D) numerical model. Further the trapping and acceleration of an externally injected test electron, by the generated wakefields, has been studied.
The organization of the paper is as follows: Section 2 includes the 2D PIC simulation study of the generated longitudinal, electrostatic wakefield for a super-Gaussian pulse and its comparison with the wakes generated by a Gaussian pulse of the same intensity. In Section 3, 1D numerical analysis has been presented to validate the results obtained via simulation study. The trapping and energy gain due to the acceleration of an externally injected test electron by the generated wakefields has also been studied. Section 4 presents summary and discussion.
2. 2D PIC SIMULATION
In order to study the generation of longitudinal electrostatic wakefields via passage of super-Gaussian laser pulse through cold, homogeneous and underdense plasma, we have performed 2D PIC simulations using XOOPIC code (Verboncoeur et al., Reference Verboncoeur, Langdon and Gladd1995). The temporal profile of the laser pulse is considered to be of the form a = a 0 exp (−(ξ − ξ0)2m /L 2m) (where m = 2, 3, 4 … for super-Gaussian while m = 1 represents a Gaussian profile). Here, L and ξ0 are, respectively, the pulse length and arbitrary pulse center of the laser pulse. The full width at half maximum (FWHM) pulse length 
$L_{FWHM} \lpar\!\! =\! \sqrt {2\ln 2} L\rpar $ was considered to be 14.2 µm, corresponding to L = 12.0 µm. In the present simulation study, the plasma wavelength is taken to be λp = 32 µm (=2πc/ωp, where ωp = (4π n 0e 2/m)1/2 is the plasma frequency and n 0 = 1.09 × 1018/cm 3 is the plasma electron density). We have performed the simulations in the relativistic regime of the laser pulse intensity 2.14 × 1018W/cm 2 that corresponds to a 0 = 1.0, for a laser frequency of ω 0 = 2.355 × 1015Hz (corresponding to a wavelength of 800 nm). Considering the laser beam to be broad (k pr 0 ≫1), we have assumed the transverse laser spot size (r 0) to be 80 µm.
The 2D simulation box is 80 µm long along the laser propagation direction (x) and 400 µm wide along the transverse direction (y). We use a spatial mesh of 2048 × 512 cells with 2 × 107 electrons. The time step (satisfying the Courant condition) is taken to be 0.07 fs. The ions are assumed to be stationary, forming a neutralizing background fluid throughout the simulation process. We have performed the simulation taking m = 2 super-Gaussian pulse and compared it with a Gaussian profile. A moving window was employed in the simulation study to reduce the computation time.
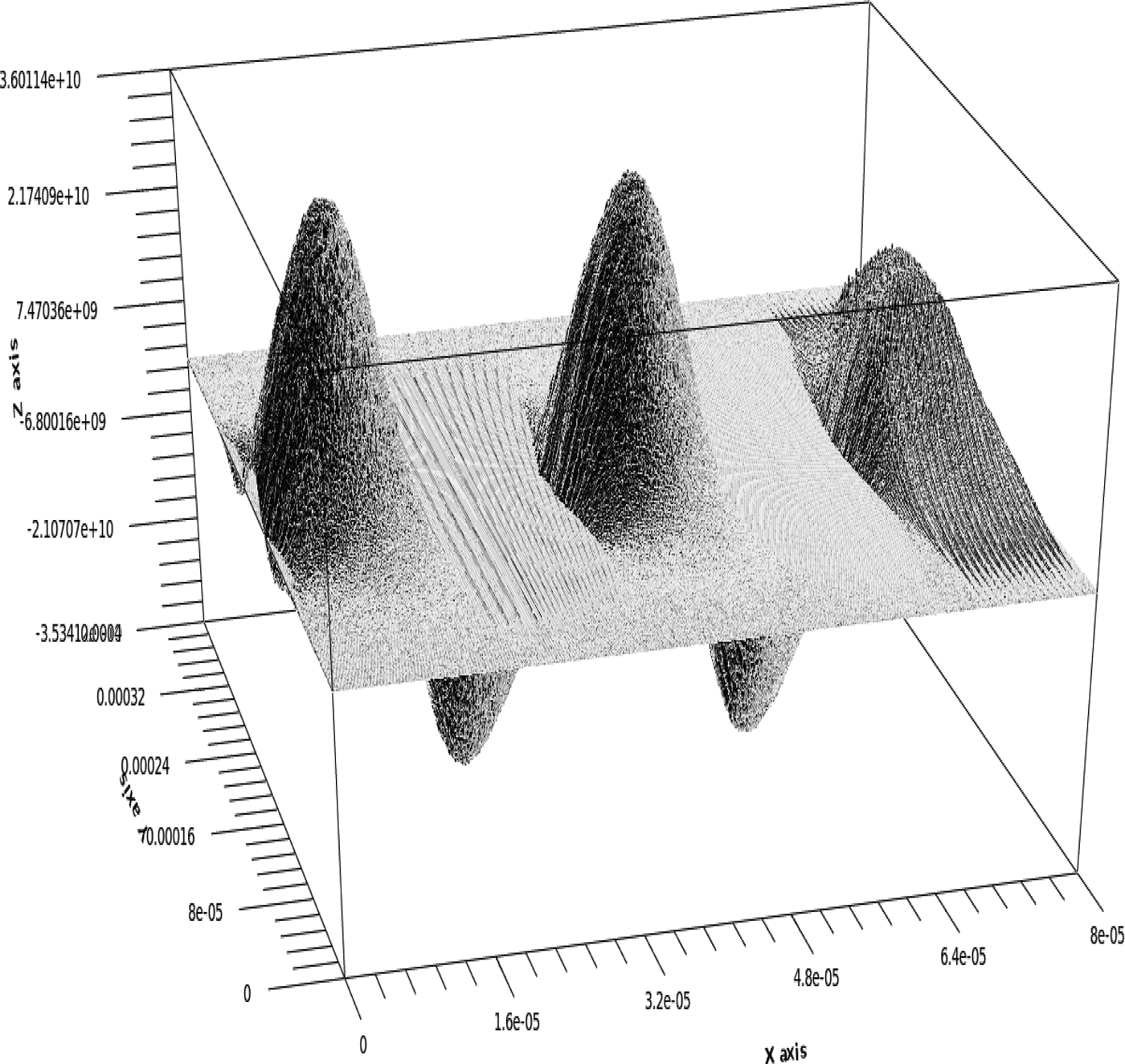
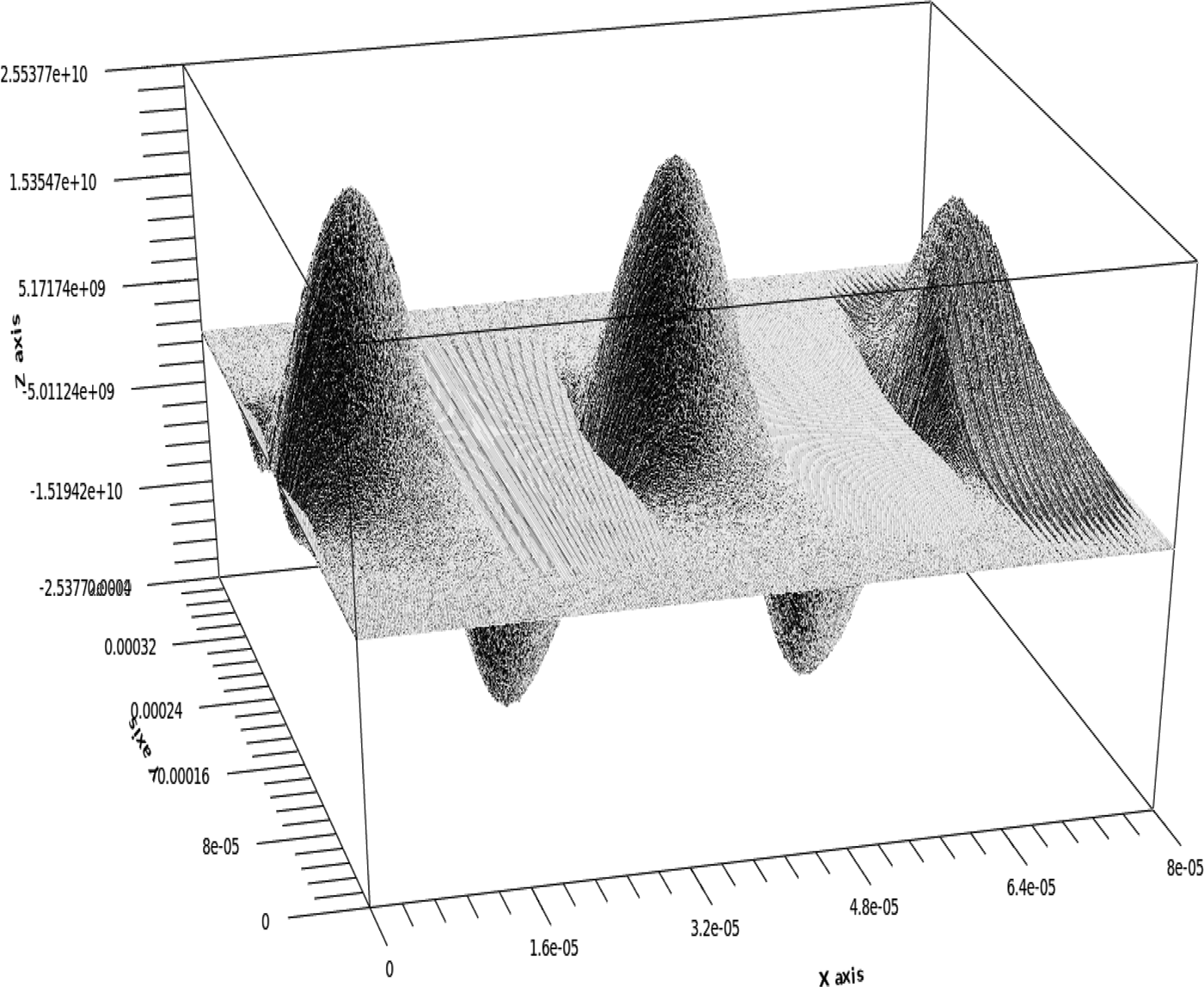
The 2D plots obtained via PIC simulations, showing the variation of generated electric field amplitude with respect to the longitudinal and transverse distances for super-Gaussian and Gaussian laser pulses are shown in Figures 1 and 2, respectively. It may be noted that the wake amplitude is maximum on-axis and decreases with increase in transverse distance. Comparing Figures 1 and 2, it is seen that the peak amplitude of the wakes obtained with super-Gaussian laser pulse is more than the wakefield amplitude generated by a Gaussian pulse. Further, in Figure 3, we plot the 1D curves depicting the excitation of normalized longitudinal electrostatic wakes with normalized distance k px at y = 0 i.e., on-axis. The curves a and b here depict the wakefield amplitudes generated via super-Gaussian and Gaussian laser pulses, respectively. An increase of 23.3% in the normalized wakefield amplitude of the wakes generated by super-Gaussian pulse as compared to the Gaussian pulse case has been seen. The increase in the normalized peak amplitude of the generated electric field by super-Gaussian pulse as compared to the wake amplitude excited by Gaussian laser pulse of the same intensity occurs because the gradient for super-Gaussian pulse is more in comparison with the Gaussian pulse case.
Fig. 1. 2D PIC simulation study showing the variation of normalized longitudinal electrostatic wakefield (E nx) for super-Gaussian laser pulse for a 0 = 1.0, λp = 32 µm and L = 12 µm.
Fig. 2. 2D PIC simulation study showing the variation of normalized longitudinal electrostatic wakefield (E nx) for Gaussian laser pulse for a 0 = 1.0, λp = 32 µm and L = 12 µm.
Fig. 3. (Color online) 1D plot obtained from PIC simulation at y = 0, showing the variation of normalized longitudinal electrostatic wakefield (E nx) with k px for super-Gaussian (curve a) and Gaussian (curve b) laser pulses for a 0 = 1.0, λp = 32 µm and L = 12 µm.
3. 1D NUMERICAL MODEL
3.1. Validation of Results Obtained Via Simulation Study
In order to validate the results obtained via 2D PIC simulation studies, we have developed a 1D numerical model. Consider a linearly polarized laser pulse represented by the vector potential 
$\vec{A} = \hat{x}A_0 \lpar z\comma \; t\rpar \cos \lpar k_0 z - {\rm \omega} _0 t\rpar $ (where A 0, k 0, and ω0 are, respectively, the amplitude, wave number and frequency of the laser pulse) propagating through uniformly pre-ionized plasma having ambient density n 0 along the positive z-direction.
Wakefield generation due to the interaction of laser pulses with cold and relativistic plasma is governed by basic nonlinear fluid equations,
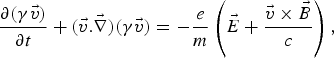$$\displaystyle{\partial \lpar {\rm \gamma} \vec{v}\rpar \over \partial t} + \lpar \vec{v}.\vec{\nabla}\rpar \lpar {\rm \gamma} \vec{v}\rpar = - \displaystyle{e \over m} \left(\vec{E} + \displaystyle{\vec{v} \times \vec{B} \over c} \right)\comma \;$$
$$\displaystyle{\partial n_e \over \partial t} + \vec{\nabla}.\lpar n_e \vec{v}\rpar = 0\comma \;$$and
$$\nabla^2 \Phi = k_p^2 \lpar n_e - 1\rpar \comma \;$$
where γ (=(1 − v 2/c 2)−1/2) is the relativistic factor and 
$\vec{v}$ & n e are, respectively, the velocity and density of plasma electrons under the influence of the perturbing laser field. In the present study, we have considered the electric and magnetic fields of the form 
$\vec{E} = - \displaystyle{1 \over c} \displaystyle{\partial \vec{\rm A} \over \partial t} - \vec{\nabla} \Phi$ and 
$\vec{B} = \vec{\nabla} \times \vec {\rm A}$, where 
$\vec{\rm A}$ and Φ are, respectively, the vector potential of the laser pulse and the scalar potential of the generated field.
In order to study the generation of wakefields, Eq. (1) is used to obtain the governing equations for the evolution of the longitudinal and transverse plasma electron velocities as,
$$\displaystyle{\partial \lpar {\rm \gamma} v_z \rpar \over \partial t} + v_z \displaystyle{\partial \lpar {\rm \gamma} v_z\rpar \over \partial z} = \displaystyle{e \over m} \left[\displaystyle{\partial \Phi \over \partial z} - \displaystyle{v_x \over c} \displaystyle{\partial A_0 \over \partial z} \right]\comma \;$$
$$\displaystyle{\partial \lpar {\rm \gamma} v_x\rpar \over \partial t} + v_z \displaystyle{\partial \lpar {\rm \gamma} v_x\rpar \over \partial z} = \displaystyle{e \over mc} \left[\displaystyle{\partial A_0 \over \partial t} + v_z \displaystyle{\partial A_0 \over \partial z} \right].$$While writing Eqs. (4), we have retained the terms that oscillate at the plasma frequency and neglected the terms comprising of oscillations at the laser frequency.
We proceed by transforming the plasma fluid equations (Eqs. (2) and (3)) including the modified Lorentz force equation (Eqs. (4)), to a frame moving with the group velocity 
$\lpar v_g \approx c\lpar 1 - {\rm \omega}_p^2 / 2{\rm \omega}_0^2\rpar \rpar $ of the laser pulse. These equations are hence written in terms of independent variables τ = t and ξ = z − v gt. Further, using quasi-static approximation (QSA) (Esarey et al., Reference Esarey, Sprangle, Krall and Ting1997), the explicit dependence of fluid equations on τ is neglected. Hence, the transformed, normalized fluid equations governing the evolution of the electrostatic wakefield are given by,
$$\displaystyle{\partial u_z \over \partial \lpar k_p {\rm \xi}\rpar } = \displaystyle{1 \over {\rm \gamma} \lpar u_z - {\rm \beta}_g \rpar } \left[\displaystyle{\partial {\rm \phi} \over \partial \lpar k_p {\rm \xi}\rpar } - u_x \displaystyle{\partial a_0 \over \partial \lpar k_p {\rm \xi} \rpar } \right]- \displaystyle{u_z \over {\rm \gamma}} \displaystyle{\partial {\rm \gamma} \over \partial \lpar k_p {\rm \xi}\rpar }\comma \;$$
$$\displaystyle{\partial u_x \over \partial \lpar k_p {\rm \xi}\rpar } = \displaystyle{1 \over {\rm \gamma}} \left[\displaystyle{\partial a_0 \over \partial \lpar k_p {\rm \xi}\rpar } - u_x \displaystyle{\partial {\rm \gamma} \over \partial \lpar k_p {\rm \xi}\rpar } \right]\comma \;$$
$$\displaystyle{\partial ^2 {\rm \phi} \over \partial \lpar k_p {\rm \xi}\rpar ^2} = n - 1\comma \;$$
$$\displaystyle{\partial n \over \partial \lpar k_p {\rm \xi} \rpar } = - \displaystyle{n \over \lpar u_z - {\rm \beta} _g\rpar } \displaystyle{\partial u_z \over \partial \lpar k_p {\rm \xi}\rpar }\comma \;$$where φ (=eΦ/mc 2), n(=n e /n o) and βg (=v g/c) are, respectively, the normalized scalar potential of the generated wakefield, plasma electron density and group velocity of the laser pulse. While, a 0 (=eA 0 /mc 2) is the normalized amplitude of the vector potential of the laser pulse. Eqs. (5) are valid for arbitrary pulse profiles and pump strengths and can be solved simultaneously using the fourth order Runge-Kutta numerical technique. Using the same parameters as used in the simulation study, the normalized wake potential and hence the electrostatic longitudinal wakefield 
$\lpar E_{nz} = -\vec{\nabla} {\rm \phi} \rpar $ may be obtained.
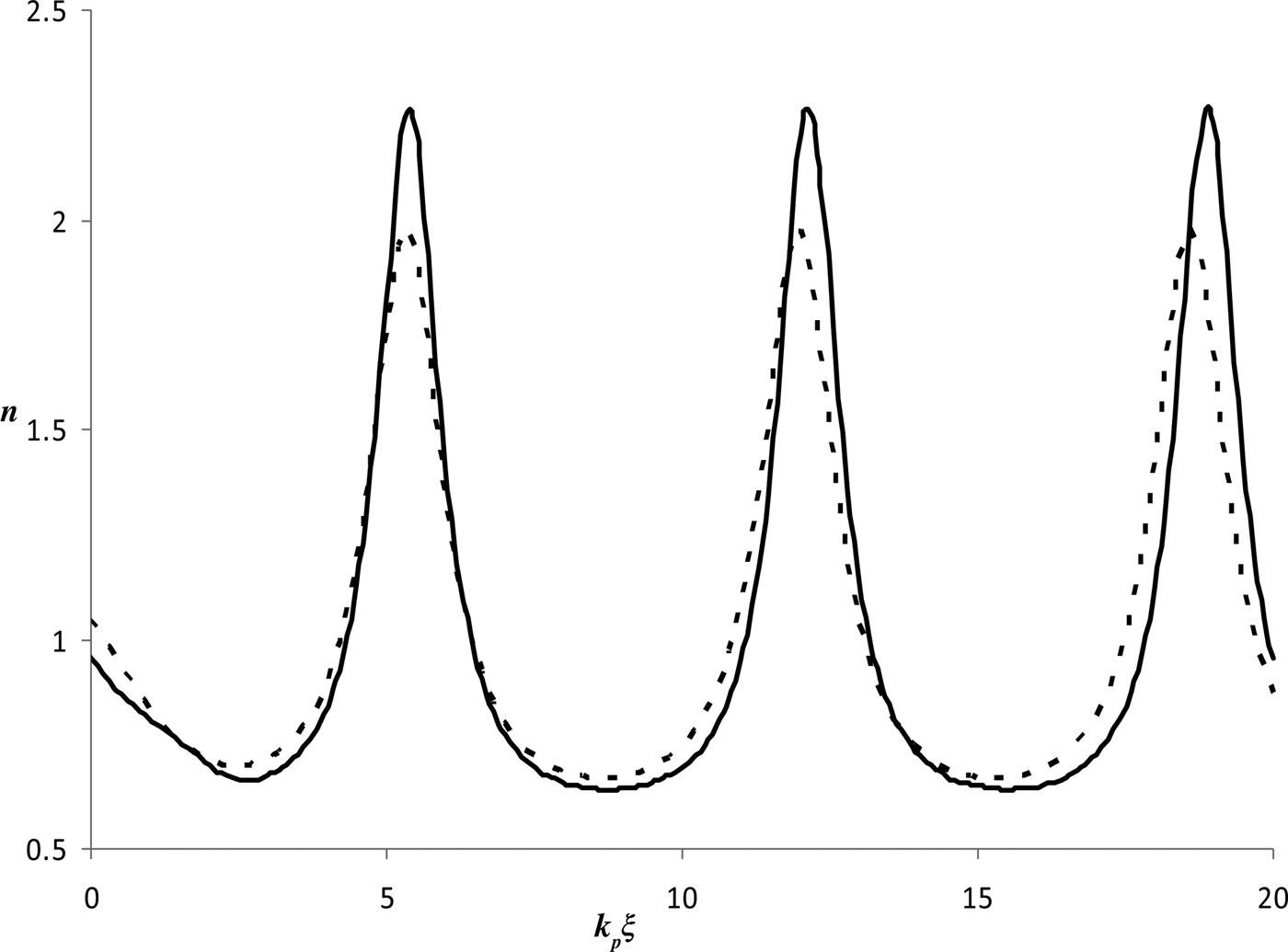
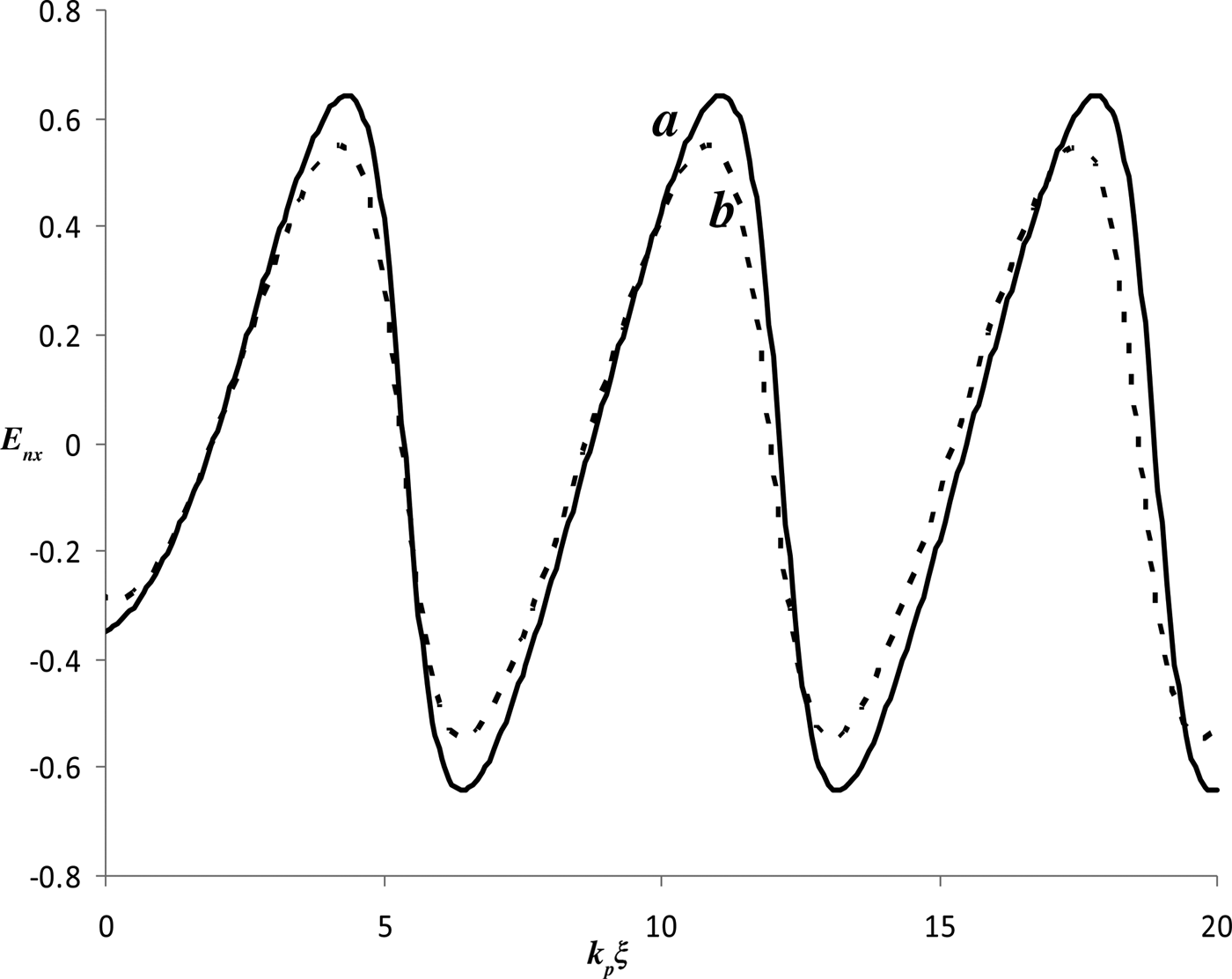
In Figure 4, solid and dotted curves, respectively, show the variation of normalized plasma electron density with respect to k pξ for super-Gaussian and Gaussian pulses. It is seen that there is an enhancement of 21.9% in the perturbed plasma electron density generated due to a super-Gaussian pulse as compared to the density curve obtained with Gaussian laser pulse Similarly, Figure 5 depicts the variation of normalized, longitudinal, electrostatic wakefield (E nz) with k pξ, generated due to super-Gaussian as well as Gaussian laser pulses. Curve a (b) represents the longitudinal wakefield generated behind the super-Gaussian (Gaussian) pulse. Comparing curves a and b in Figure 5, an increase of 20.4% is seen in the amplitude of the generated wakefield via super-Gaussian laser pulse as compared to the Gaussian pulse case. Comparing Figures 3 and 5, the results obtained via numerical studies and simulations are found to be in good agreement with each other. However, the slight difference in the wakefield amplitudes obtained via simulation in comparison with the 1D numerical results may be attributed to 2D nonlinear effects.
Fig. 4. Variation of normalized plasma electron density (n) with k pξ for super-Gaussian (solid curve) and Gaussian (dotted curve) laser pulses for the same parameters as used in Figure 1.
Fig. 5. Variation of normalized longitudinal electrostatic wakefield (E nz) with k pξ for super-Gaussian (curve a) and Gaussian (curve b) laser pulses for the same parameters as used in Figure 1.
3.2. Acceleration of an Externally Injected Test Electron
Further, the acceleration mechanism of a test electron injected behind the laser pulse is studied. The exchange of energy between the generated axial wakefield and the test electron can be obtained with the help of Hamiltonian dynamics (Esarey & Pilloff, Reference Esarey and Pilloff1995). Following Esarey and Pilloff (Reference Esarey and Pilloff1995), Hamilton's equation along with the energy conservation Eq. (7) gives the peak energy (γe) of the test electron as
$${\rm \gamma}_e = {\rm \gamma}_p \lpar 1 + {\rm \gamma}_p \Delta {\rm \phi} \rpar \pm {\rm \gamma}_p {\rm \beta} _p \lsqb \lpar 1 + {\rm \gamma}_p \Delta {\rm \phi} \rpar ^2 - 1\rsqb ^{1 / 2}\comma \;$$where Δφ = φ− φmin and ± gives γe (max) and γe (min), respectively. Since, the external test electron is assumed to be driven by the generated plasma wave, so the initial velocity of the injected test electron is taken to be equal to the phase velocity (v p) of the plasma wave. This corresponds to initial particle energy (γi) of the test electron to be equal to γp (=(1 − βp2)−1/2). An important characteristic of the phase space is the separatrix that defines the limit between the trapped and untrapped electron orbits in the phase space. In order to plot the separatrices characterizing the just trapped test electron in the phase space, we inject the test electron where the wake potential is minimum.
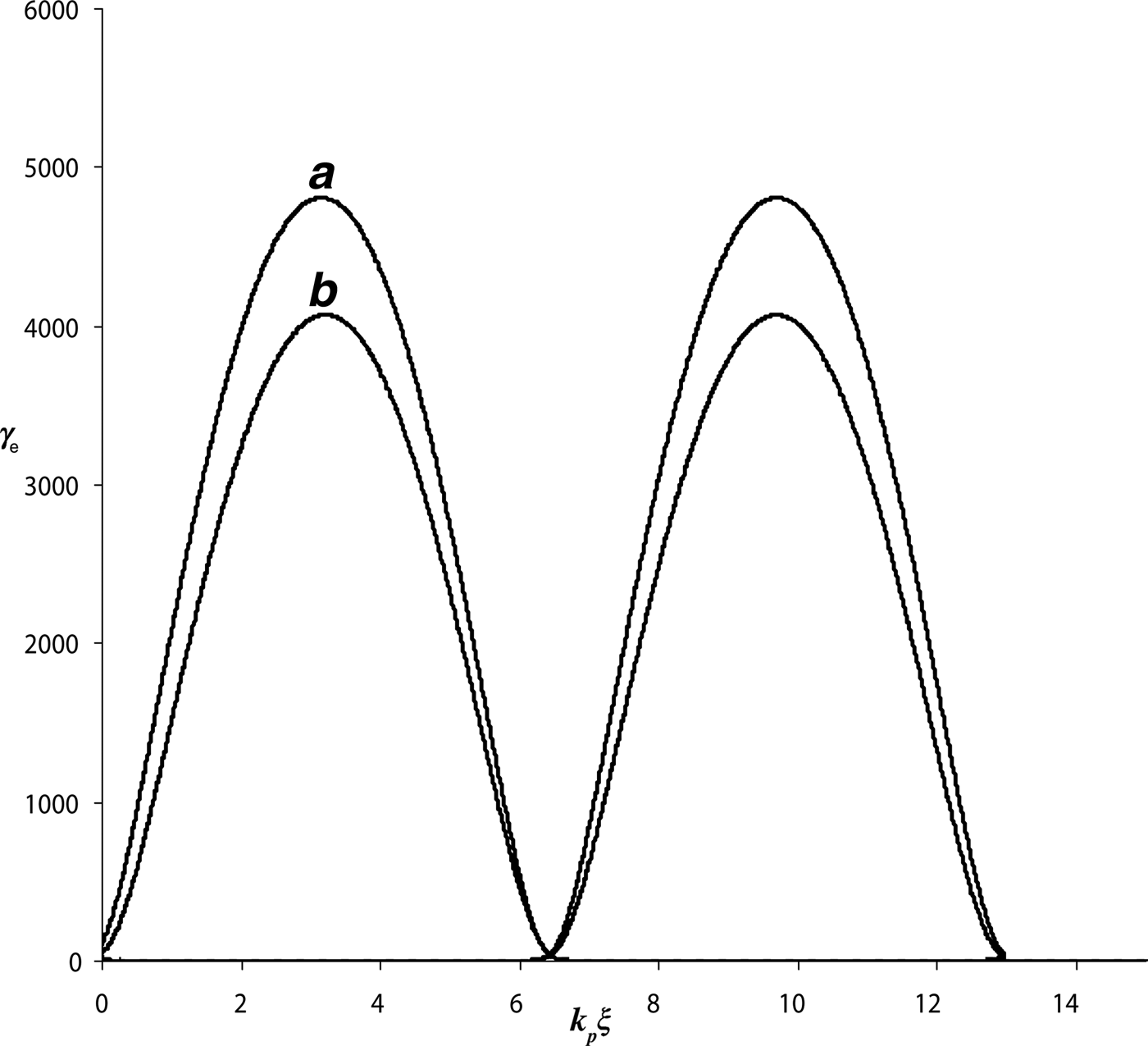
In the present analysis, we have considered the group velocity of the laser pulse (v g) to be nearly equal to the phase velocity of the plasma wave (v p). The separatrix plots for the test electron being accelerated by the super-Gaussian as well as Gaussian laser pulses are plotted by simultaneously solving Eqs. (6) along with transformed plasma fluid equations using fourth order Runge-Kutta algorithm. Plots a & b in Figure 6, depict the separatrix curves traced by an externally injected test electron being driven by the wakes generated by the super-Gaussian and Gaussian laser pulses, respectively. The injection positions (φmin, k pξ) of the test electron for tracing the separatrix curves a and b are, respectively (−0.48527, 12.97) and (−0.43964, 12.93). The injection energies necessary for trapping the test electron excited by the wakes generated by super-Gaussian and Gaussian laser pulses is same (=20.47 MeV), while the maximum energies attained after acceleration are 2.46 GeV, and 2.08 GeV for curves a and b, respectively. Hence, a gain of 15.4% in the maximum energy of the accelerated test electron is seen for super-Gaussian pulse as compared to Gaussian pulse case.
Fig. 6. Separatrices plots for the test electron driven by wakes generated by super-Gaussian (curve a) and Gaussian (curve b) laser pulses.
In order to evaluate the effective gain in electron energy, we define the gain 
$g = \displaystyle{{\rm \gamma} _e - {\rm \gamma}_p \over {\rm \gamma}_p}$. The gain is calculated to be 119.22 and 100.75 for two cases taking super-Gaussian and Gaussian laser pulse, respectively, as the driving source. Therefore, an increase of 15.5% in the energy gain of the test electron being accelerated by wakes generated by super-Gaussian laser pulse is observed over the gain attained by accelerating the test electron by wakes driven by Gaussian laser pulse.
4. SUMMARY AND DISCUSSION
Generation of longitudinal electrostatic wakefields by the interaction of super-Gaussian laser pulse with homogeneous plasma has been presented via 2D PIC simulations in the relativistic regime. It is observed that the generated wake amplitude for super-Gaussian driving laser pulse show a remarkable increase as compared to the wakefield amplitude for a Gaussian laser pulse.
In order to validate the results obtained via 2D PIC simulation studies, we have developed a 1D numerical model. This model comprises of fundamental fluid equations and its further, reduction to the transformed fluid equations having time independent form using quasi-static approximation. The reduced non-linear fluid equations are hence solved simultaneously using fourth order Runge-Kutta numerical technique to study the generation of longitudinal electrostatic wakefields. The wakefields generated due to super-Gaussian laser pulse are then compared to the wakes driven by Gaussian laser pulse. The results obtained via numerical studies and simulations are found to be in good agreement with each other.
Further, the trapping and acceleration of an externally injected test electron has been studied. The peak energy attained by the test electron being accelerated by the wakes generated by a super-Gaussian laser pulse is evaluated and compared with the Gaussian pulse case. In the present analysis we take the initial injection energy of the test electron to be equal to the energy of the plasma wave which depends on the phase velocity of the plasma wave. Since the group velocity of the laser pulse (v g) and the phase velocity of the plasma wave (v p) are taken to be taken to be equal and the group velocity of the laser pulse is independent of laser pulse shapes hence the injection energies (=γpmc 2) of test electron accelerated by wakes generated through different pulse shapes is equal. Comparing the difference between the peak energies attained by the test electron and injection energies for two different pulse shapes, we see that the energy gain is appreciably enhanced for test electron accelerated by wakes generated by super-Gaussian pulse as compared to the energy gain for Gaussian pulse case.
Thus, it may be concluded that the super-Gaussian laser pulse is capable of enhancing the wake amplitude and hence the peak energy of the test electron driven by electrostatic longitudinal wakefield as compared to the Gaussian pulse case of same intensity.
ACKNOWLEDGEMENTS
The authors acknowledge the financial support provided by Science and Engineering Research Council, Department of Science and Technology, Government of India vide Project No.-SR/S2/HEP-22/2009.
