1. INTRODUCTION
The interactions between ion beams and plasmas have been extensively studied in recent years. These studies have been a topic of great interest due to their significant applications in modern sciences and technologies, such as the heavy-ion inertial fusion (HIF) (Renk et al., Reference Renk, Mann and Torres2008; Ter-Avetisyan et al., Reference Ter-Avetisyan, Schnuerer, Polster, Nickles and Sandner2008; Zhao et al., Reference Zhao, Hu, Cheng, Wang, Peng, Golubev, Zhang, Lu, Zhang, Zhou, Wang, Xu, Ren, Li, Lei, Sun, Zhao, Wang, Wang and Xiao2012), the neutral beam injection in the magnetically confined fusion plasmas (Thompson et al., Reference Thompson, Stork and Deesch1993; Takahashi et al., Reference Takahashi, Kato, Kondoh and Iwasawa2004) and the cooling of heavy-ion beams by electrons (Sorensen & Bonderup, Reference Sorensen and Bonderup1983; Goldman & Hofmann, Reference Goldman and Hofmann1990), etc.
In the last decade, many experimental (Dietrich et al., Reference Dietrich, Hoffmann, Boggasch, Jacoby, Wahl, Elfers, Haas, Dubenkov and Golubev1992; Jacoby et al., Reference Jacoby, Hoffmann, Laux, Muller, Wahl, Weyrich, Boggasch, Heimrich, Stockl, Wetzler and Miyamoto1995; Hoffmann et al., Reference Hoffmann, Jacoby, Laux, Demagisteis, Boggasch, Spiller, Stockl, Tauschwitz, Weyrich, Chabot and Gardes1994) and theoretical (Gryzinski, Reference Gryzinski1957; Butler & Buckingham, Reference Butler and Buckingham1962; Peter & Meyertervehn, Reference Peter and Meyertervehn1991; Boine-Frankenheim & D'avanzo, Reference Boine-Frankenheim and D'avanzo1996; D'Avanzo et al., Reference D'avanzo, Hofmann and Lontano1998; Zwicknagel et al., Reference Zwicknagel, Reinhard, Seele and Toepffer1996a; Reference Zwicknagel, Toepffer and Reinhard1996b; Reference Zwicknagel, Toepffer and Reinhard1999; Oguri et al., Reference Oguri, Hasegawa, Kaneko, Ogawa and Horioka2005; Hu et al., Reference Hu, Song and Wang2009) investigations have been made to understand the interactions of a single-charged particle with plasmas. The interaction process is usually characterized by the ion–plasma coupling strength Z = Z p/N D, where Z p is the charge state of the ion and N D the number of electrons in a Debye sphere. For the weak ion–plasma coupling Z ≪ 1, the linearized theories, such as the dielectric (Peter & Meyertervehn, Reference Peter and Meyertervehn1991; Zwicknagel et al., Reference Zwicknagel, Toepffer and Reinhard1999) and binary collision (Gryzinski, Reference Gryzinski1957; Butler & Buckingham, Reference Butler and Buckingham1962) theories, are used to investigate the stopping power of an ion in plasmas. For strong ion–plasma coupling Z ≥ 1, the particle-in-cell (PIC) method (Boine-Frankenheim & D'avanzo, Reference Boine-Frankenheim and D'avanzo1996; D'Avanzo et al., Reference D'avanzo, Hofmann and Lontano1998; Hu et al., Reference Hu, Song and Wang2009) and molecular-dynamics method (Zwicknagel et al., Reference Zwicknagel, Reinhard, Seele and Toepffer1996a; Reference Zwicknagel, Toepffer and Reinhard1996b; Oguri et al., Reference Oguri, Hasegawa, Kaneko, Ogawa and Horioka2005) are used to study the influences of nonlinear effects on the interaction process.
Recently, the interactions between the ion beam pulses and plasmas have received more and more attention (Hoffmann et al., Reference Hoffmann, Blazevic, Ni, Rosmej, Roth, Tahir, Tauschwitz, Udrea, Varentsov, Weyrich and Maron2005; Zhao et al., Reference Zhao, Hu, Cheng, Wang, Peng, Golubev, Zhang, Lu, Zhang, Zhou, Wang, Xu, Ren, Li, Lei, Sun, Zhao, Wang, Wang and Xiao2012; Hu et al., Reference Hu, Song, Zhao and Wang2013). Ion beam pulses are frequently used in many applications, such as HIF (Renk et al., Reference Renk, Mann and Torres2008; Ter-Avetisyan et al., Reference Ter-Avetisyan, Schnuerer, Polster, Nickles and Sandner2008; Zhao et al., Reference Zhao, Hu, Cheng, Wang, Peng, Golubev, Zhang, Lu, Zhang, Zhou, Wang, Xu, Ren, Li, Lei, Sun, Zhao, Wang, Wang and Xiao2012) and high-density laser-produced proton beams for the fast ignition of inertial confinement fusion targets (Krushelnick et al., Reference Krushelnick, Clark, Allott, Beg, Danson, Machacek, Malka, Najmudin, Neely, Norreys, Salvati, Santala, Tatarakis, Watts, Zepf and Dangor2000). In these applications, the wakefield (Keinigs & Jones, Reference Keinigs and Jones1987; Hu et al., Reference Hu, Song and Wang2012; Franchetti et al., Reference Franchetti, Hofmann, Fischer and Zimmermann2009) and stopping power (Deutsch & Fromy, Reference Deutsch and Fromy1995; Zwicknagel & Deutsch, Reference Zwicknagel and Deutsch1997; Boine-Frankenheim et al., Reference Boine-Frankenheim, Gjonaj, Petrov, Yaman, Weiland and Rumolo2012; Hu et al., Reference Hu, Song and Wang2012) are important quantities, due to the reason that they have close relation to the energy transferred from the ion beams to plasmas. G. Zwicknagel and C. Deutsch (Zwicknagel & Deutsch, Reference Zwicknagel and Deutsch1997) have investigated the correlation effects between the pulse ions on the wakefield and stopping power using the dielectric theory. It is shown that the correlation effects play important roles in determining the stopping power, and the influence of correlation effects should be taken into consideration. In addition to the correlation effects, the beam parameters, such as the beam velocity and density, also have significant effects on the beam–plasma interactions (Deutsch & Fromy, Reference Deutsch and Fromy1995). To our knowledge, there are few investigations (Deutsch & Fromy, Reference Deutsch and Fromy1995; Boine-Frankenheim et al., Reference Boine-Frankenheim, Gjonaj, Petrov, Yaman, Weiland and Rumolo2012) on the effects of the beam density and velocity on the wakefield and stopping power. Furthermore, most of these investigations are focused on the high-energy ion beam pulse (Boine-Frankenheim et al., Reference Boine-Frankenheim, Gjonaj, Petrov, Yaman, Weiland and Rumolo2012). However, the low-energy ion beam pulses, where the projectile ion velocity is close to the Bohr velocity of bound electrons and in the vicinity of the plasma electron thermal velocity, are also important because they can be produced more easily and efficiently. In addition, The investigations of low-energy beams propagation in plasmas have a variety of important applications. For instance, the intense low-energy beams are highly unstable to the transverse dispersion due to the Coulomb repulsion among the pulse ions. It is found that the plasma electrons tend to neutralize the strong repulsive space-charge force among the pulse ions. The background plasma can be provided as an ideal media for ion beam pulse focusing and transport. I. D. Kaganovich (Kaganovich et al., Reference Kaganovich, Startsev and Davidson2004) have found that for long, nonrelativistic ion beam pulse (L b ≫ V b/ωe, (where L b is the beam half-length, V b the beam velocity, and ωe the plasma electron frequency), charge neutralization is complete, and the transverse dispersion of the beam can be negligible. Thus, the investigations of low-energy beams propagation in plasmas can improve the design of the future ion accelerators based on the plasma technology. In addition, the ion energy deposition has an important characteristic, that a large part of the ion kinetic energy is deposition at the end of the range in the matter, the so-called Bragg peak, where the ion energy is low. According to the characteristic, the energy loss process of low-energy beams in plasmas is one of the important processes of the heavy-ion-driven high-energy density physics (HEDP). To make better use of the low-energy ion beam pulses in practical applications, the influence of the beam density on the wakefield and stopping power at low beam velocity need to be further studied.
In this paper, a two-dimensional (2D)-PIC simulation is carried out to study a hydrogen ion beam pulse with low drift velocity propagation in hydrogen plasmas using the code of VORPAL (Nieter & Cary, Reference Nieter and Cary2004). Both the pulse ions and plasma particles are treated by the PIC method. In this way, the correlation effects between the pulse ions are taken into consideration and the description of the interactions between the ion beam pulse and plasmas is much closer to the real physics process. Then the effects of the beam density on the wakefield and stopping power are discussed in detail. Our present study would be useful for the further theoretical and experimental works in this field.
Section 2 introduces the numerical method and physical model used in our simulation. In Section 3, the simulation results are presented and discussed. Finally, conclusions are made in Section 4.
2. NUMERICAL METHOD AND PHYSICAL MODEL
In this paper, a 2D3V electromagnetic(EM) PIC simulation is carried out to study the stopping power and wakefield for a hydrogen ion beam pulse with low drift velocity propagation in hydrogen plasmas using the code of VORPAL (Nieter & Cary, Reference Nieter and Cary2004). VORPAL is a arbitrarily dimensional, hybrid plasma, and beam simulation code. The kinetic model incorporated in VORPAL is based on the PIC algorithm. In the EM simulation, the electric and magnetic fields are obtained using the finite-difference-time-domain solver based on the Maxwell's equations. This method uses the Yee mesh and achieves second-order accuracy. Faraday's equation,
$${{\partial {\bf B}} \over {dt}} = - \nabla \times {\bf E}, $$and the Ampere-Maxwell equation,
$$\displaystyle{{\partial {\bf E}} \over {dt}} = {c^2}\nabla \times {\bf B} - \displaystyle{{\bf j} \over {{\varepsilon _0}}}, $$are updated through the finite-difference scheme. For the PIC model to be self-consistent, the amount of particle density that crosses each cell boundary is determined, and the corresponding current is then deposited on the grid. The EM field is updated using these current values. This charge-conserving current deposition algorithm enables the integration of Maxwell's equations without any additional divergence correction. Then, the electric and magnetic fields are interpolated to the location of the charged particle. The particle position and the velocity are updated using the equations of motion:
$${{d{\bf r}} \over {dt}} = {\bf v}, $$
$${{d{\bf v}} \over {dt}} = {q \over m}({\bf E} + {\bf v} \times {\bf B}), $$where r, v, q, and m are the position, velocity, charge, and mass of the charged particles. In the simulation, the average kinetic energy per pulse ion E b/Numb, where E b is the total kinetic energy of the beam and Numb the number of the pulse ions, and the average penetration depth of the beam are calculated at each time step. Then the dependence of the kinetic per pulse ion on the penetration depth in plasmas is obtained. The dropping rate is adopted to represent the stopping power per pulse ion.
A 2D3V (x, z, V x, Vy, Vz) plasma model is used in the simulation. All charged particles extend along y-direction and are represented by rods. The charged particles are considered to move in the x–z plane, with the velocity in the y direction V y also tracked, which goes partway to a 3D-model. The 2D-model is as shown in Figure 1, which is composed of the radial (x) and longitudinal (z) directions. Here the radial (x) and longitudinal (z) directions represent perpendicular and parallel to the direction of the beam motion, respectively. In the longitudinal (z) direction, the acceleration and deceleration of charged particles can be tracked. This configuration has been adopted by Hu et al. (Reference Hu, Song and Wang2010) for the simulation of the beam energy deposition and by Hu et al. (Reference Hu, Song, Zhao and Wang2013), Kaganovich et al. (Reference Kaganovich, Startsev and Davidson2004) for the study of the beam modulation and focusing. Thus, we believe that the present 2D-model can give some valuable results.
Fig. 1. The 2D-model: The propagation of the ion beam pulse in plasmas.
In order to assure that the plasma and field perturbations do not reach the boundaries, the simulation box is composed of 800 grids in the z-direction and 240 grids in the x-direction. Periodic boundary condition is adopted to simulate an infinite plasma. A fully-ionized hydrogen plasma (H +, e −) is placed in the box. The plasma is assumed to be collisionless, uniform, non-magnetized, and in a steady state. Plasma parameters used in the simulation are as follows: Initial plasma density N e0 = 2.0 × 1017 m−3, initial plasma electron temperature T e0 = 10 eV, and initial plasma ion temperature T i0 = 10 eV. Initially, the ion beam pulse with a certain profile and density is placed at the left of the simulation box. The pulse ions are taken to be H +. The beam velocity V b is 8.0 × 106 m/s. The projectile velocity is 3.65 times of the Bohr velocity and 6.15 times of the plasma electron thermal velocity. The projectile velocity is close to the Bohr velocity and the plasma electron thermal velocity within an order of magnitude. Thus, the beam in this work could be a low-energy beam. In addition, the beam half-length L b is 0.001 m. The corresponding pulse duration is 0.25 ns. At the beginning of the simulation, the beam radius R(z 0, z) is related to the coordinate in the z-direction by the relation of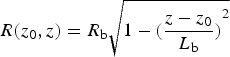 
$R({z_0},z) = {R_{\rm b}}\sqrt {1 - {{(\displaystyle{{z - {z_0}} \over {{L_{\rm b}}}})}^2}} $, where R b is set equal to 0.1 × 10 −3 m and z 0 ( = L b) is the initial center position of the beam. The density profile of the ion beam pulse is a Gaussian distribution 
${N_{\rm b}}(x,z) =$
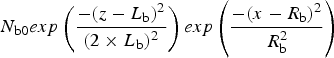$N_{{\rm b}0} exp \left(\displaystyle{{ - (z - L_{\rm b})^2} \over {(2 \times L_{\rm b})^2}} \right)exp \left(\displaystyle{{ - (x - R_{\rm b})^2} \over {R_{\rm b}^2}} \right)$, where N b0 ranges from 0.1 × 1017 to 3.0 × 1017 m−3. The corresponding peak beam current ranges from 0.1 to 3.0 mA. In addition, both the pulse ions and plasma particles are treated by the PIC method. The number of super-particles per cell is chosen to be 50 for both the pulse ions and plasma particles. The ion beam pulse is not simply regarded as a single heavy ion or a rigid bunch. The influences of interactions among the pulse ions, plasma electrons, and plasma ions are taken into consideration. With the propagating of the beam, the ion beam pulse losses energy as well as changes its profile due to the interactions between the bunch and plasmas via its longitudinal electric.
Taking into account the Courant–Friedrichs–Lewy limit, the time step Δt = 9.11 × 10 −14 s, which is much smaller than the plasma oscillation period (≈2.5 × 10 −10 s), is chosen. The spatial step Δx = Δz = 5.26 × 10 −5 m ≈ λ e, where λ e is the Debye shielding length of the plasma electrons, is chosen.
3. SIMULATION RESULTS AND DISCUSSION
The wakefield induced by the ion beam and stopping power of the ion beam have close relation to the evolution of the kinetic energy per pulse ion, which is first calculated in our 2D-PIC simulations, as shown in Figure 2. The data are plotted as a function of the penetration depth in the plasmas. For all the beam densities, it can be noted that the kinetic energy exhibits a small transient behavior at the beginning of the beam propagating in the plasmas: The kinetic energy decreases rapidly with the increase of the depth in the plasmas, while the dropping rate slows down and remains stable after the relaxation length. Thus, the stopping power for the beam propagating in the plasmas consists of two terms: A transient term and a stationary term. In this paper, we mainly discuss the effects of the beam density on the stationary stopping power, which is the average energy loss per pulse ion per unit path length after the relaxation length. It is also found that the relaxation length has no relationship to the beam density, and is roughly equal to the flight length of the beam pulse during the plasma oscillation period 2π/ωe (Zwicknagel et al., Reference Zwicknagel, Reinhard, Seele and Toepffer1996a), where 
${\omega _{\rm e}} = \sqrt {\displaystyle{{{N_{{\rm e}0}}{e^2}}/ {{\varepsilon _0}{m_{\rm e}}}}} $ is the electron plasma frequency and m e is the electron mass.
Fig. 2. Dependence of the kinetic energy per pulse ion on the penetration depth in the plasmas with different beam densities. Here, the solid line is the result for N b0 = 0.1 × 1017 m−3, the dash line for N b0 = 0.5 × 1017 m−3, the short dash dot line for N b0 = 1.0 × 1017 m−3, the dash dot line for N b0 = 1.5 × 1017 m−3, the dash dot dot line for N b0 = 2.0 × 1017 m−3, the dot line for N b0 = 2.5 × 1017 m−3, and the short dash line for N b0 = 3.0 × 1017 m−3. The formula 2πV b/ωe is the flight length of the beam pulse during the plasma oscillation period, where ωe is the electron plasma frequency.
In Figure 2, it is also shown that the stationary stopping power changes as the beam density changes. A detailed description is given in Figures 3–5. Figure 3 shows the contour plots of the plasma electron density (normalized by N e0) at time t = 3.28 ns for different beam densities: N b0 = 0.1 × 1017 m−3, 1.0 × 1017 m−3, and 2.0 × 1017 m−3. It is found that for very low densities (N b0 = 0.1 × 1017 m−3), the electron density wave is too weak to be recognized. However, for higher beam densities, as shown in Figure 3b and 3c, the damped density waves can be clearly seen behind the bunch. Besides, as the beam densities increase, the electron density fluctuations become stronger.
Fig. 3. The contour plot of plasma electron density (normalized by N e0) at time t = 3.28 ns for (a) N b0 = 0.1 × 1017 m−3, (b) N b0 = 1.0 × 1017 m−3, and (c) N b0 = 2.0 × 1017 m−3. The beam velocity V b is 8.0 × 106 m/s. e is the Debye shielding length of the plasma.
Fig. 4. Longitudinal electric field with the same parameter as in Figure 3.
Fig. 5. Dependence of the stationary stopping power on the beam density. The beam velocity V b is 8.0 × 106 m/s. The filled squares are the Vorpal simulation results. The line is the linear fitting results of the simulation data.
Figure 4 shows the corresponding longitudinal electric field induced by the beam, with the same parameter as in Figure 3. The main features observed in Figure 3 are reproduced in Figure 4. It is also noted in Figure 4b and 4c that the first oscillation behind the bunch is particularly stronger than others, especially for high beam densities. This is because, when the beam of positively charged particles moves slowly through the plasmas, plasma electrons have much time to experience the beam's attraction and are accelerated to the beam, which results in the strong electric field around the beam. After the positive ion beam transports away, the polarized electrons diffuse due to the large repulsive space-charge force, which reduces the electric field. In addition, the beam with higher density attracts more plasma electrons, which results in the stronger oscillation. Furthermore, it is noted that the wavelength of the oscillation is the same for all the beam densities, and is roughly equal to 0.002 m, which corresponds well to the flight length of the beam pulse during the plasma oscillation period 2π/ωp (Chen et al., Reference Chen, Dawson, Huff and Katsouleas1985).
Figure 5 shows the dependence of the stationary stopping power on the beam density. It is noted that the absolute value of the stopping power is proportional to the beam density in both the linear region (N b0 < N e0) and semilinear region (N b0 ≥ N e0). This can be explained from the corresponding wakefield induced by the beam, as shown in Figures 3 and 4. The attracted plasma electrons pull back the positive pulse ions and give rise to the stopping power. The higher beam density, the more plasma electrons are attracted and the larger stopping power is obtained. Furthermore, the difference in the stopping power is basically due to the difference in correlation effects (Deutsch & Fromy, Reference Deutsch and Fromy1995). These results imply that at low beam velocities, the correlation contribution to the stopping power increase linearly as the beam density increases.
4. CONCLUSIONS
In this paper, the wakefield and stopping power for a hydrogen ion beam pulse with low drift velocity propagation in hydrogen plasmas are studied using the PIC simulation. Both the pulse ions and plasma particles are treated by the PIC method to take correlation effects into consideration. Our results show that the stopping power consists of two terms: A transient term and a stationary term. The stationary stopping power is the average energy loss per pulse ion per unit path length after the relaxation length. Special attention is paid on the effects of the beam density on the stationary stopping power and the corresponding oscillation wakefield. It is found that for very low densities, the electron density wave is too weak to be recognized. However, as the beam densities increase, the electron density fluctuations and longitudinal electric field become stronger. In addition, the first oscillation wakefield behind the bunch is particularly stronger than others, especially for high beam densities. The wavelength of the oscillation corresponds well to the flight length of the beam pulse during the plasma oscillation period. Furthermore, it is found that the stationary stopping power is proportional to the beam density in the linear/semilinear region. Our results imply that at low beam velocities, the correlation contribution to the stopping power increase linearly with the increase of the beam density.
In view of the practical applications, the study could be extended to applications in the heavy-ion-driven HEDP. Our results show that at low beam velocity, the ion beam pulses with high density are much better choices in these applications due to the more energy transferred from the ion beams to plasmas.
ACKNOWLEDGMENTS
This work was supported by the National Magnetic Confinement Fusion Science Program of China (Grant No. 2014GB104002), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA03030100), and the National Natural Science Foundation of China (Grant Nos 11275156 and 11047010).
