1. INTRODUCTION
In order to use a high-energy and short-pulse laser-plasma interaction
for direct-drive laser fusion, we are obliged to reduce a number of
setbacks received from the experimental observation. Such a problem was
caused by non-linear and anomalous phenomena and was mentioned in the
1960s and 1970s.
The major obstacles to achieving a direct-drive fusion are
Rayleigh–Taylor instability and stochastic pulsation. For the last
year, a lot of efforts were made by many research groups all over the
world in order to reduce the second effect. For example, in the paper of
Boreham et al. (1997), basing on
genuine two-fluid model, it investigated interaction between three
wave-set with plasma, leading to reduction of rippling amplitude for long
pulses with τL > 20 ps and for beam intensity
in the range 1015 W/cm2 to 1016
W/cm2.
The stochastic pulsation was recognized from numerical studies in 1974
at the University of Rochester (Hora, 1991:
Figs. 10.10 and 10.11; Hoffmann et al.,
1990) and measured most convincingly by Maddever et al.
(1990). The theory (Hora
& Aydin, 1992) confirmed this mechanism and how this could be
overcome by laser beam smoothing, especially by broad band irradiation
(Hora & Aydin, 1999; Osman & Hora, 2004). The following approach is
specifically directed to analyze new developments of the plasma block
generation (Hora et al., 2002; Badziak
et al., 2004a, 2004b) as an alternative scheme for laser
fusion (Hora, 2004) as one option of fast
ignition (Bauer, 2003; Deutsch, 2004; Mulser &
Schneider, 2004; Mulser & Bauer,
2004; Osman & Hora, 2004; Ramirez et al., 2004; Hoffmann et al., 2005; Badziak et al., 2005).
Due to fast progress in laser technology, there are in use now laser
systems generating pico and sub-pico second pulses with intensities above
1016 W/cm2. In this paper the results of
numerical computations of rippling smoothing for the laser intensity range
1016–1018 W/cm2 and short-pulse
(<10 ps) interaction with plasma are described.
2. THE WAYS OF REDUCTION OF STOCHASTIC
PULSATION
The mechanism of stochastic pulsation was first explained in 1974 when
the mentioned phenomena were bound with interaction between laser field
and plasma. Due to a big value of ponderomotive force, it is possible to
observe rippling of electrons and ions density profiles. Such a
self-generated von-Laue grating prevents the propagation of laser
radiation through the plasma and prevents energy deposition to the
critical region of plasma. Due to a thermal relaxation, gratings disappear
after some time and all the phenomenon can repeat again if the interaction
time is sufficiently long.
In order to interrupt this pulsation for long laser pulses smoothing
methods are usually used. The most popular of them are:
- Random phase plate (RPP) (Kato et
al., 1984)—generation of beamlets with random phase
shift. Standing wave pattern generated by one beamlet is washed out by the
neighboring beamlet,
- Induced special incoherence (ISI) (Lehmberg & Obenschain, 1983)—if the
coherence of laser beam is correlated with the period of arising of
standing wave no density ripple can be produced,
- Broad-band laser irradiation (Deng et al., 1986a, 1986b)—when some waves with different
frequency simultaneously pass through plasma rippling is
suppressed.
In this paper, the last method of smoothing is investigated.
Broad-band irradiation was simulated by analyzing the interaction between
three or five wave-sets with plasma. The difference between frequencies of
waves in wave-set was in the range 0.5–2.0% of
ω0.
3. TWO-FLUID HYDRODYNAMIC MODEL
The interaction of a short laser pulse with an inhomogeneous plasma
layer was investigated by Glowacz et al. (2004) with the use of the computation code of the
advanced two-fluid plasma model. This model is based on the nontermalized
direct electromagnetic interaction between the laser light and the fully
ionized plasma. In this model, electrons and ions are treated as separate
conductive fluids which interact between each other by collisions
(momentum exchange) and the Coulomb interaction. The electron and ion
fluids are described by six quantities which are mass densities
(ρe, ρi), temperatures
(Te, Ti), and
velocities of electrons and ions (υe,
υi). The equations of the model were solved in
one dimension which means that all just mentioned quantities depend on one
spatial coordinate (x) and time (t). The velocities
υe and υi are in the
x-direction.
To obtain these six quantities we solved six equations and
particularly: the equations of continuity for electrons and ions
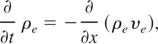
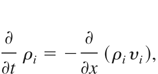
the equations describing conservation of momentum for electrons and
ions
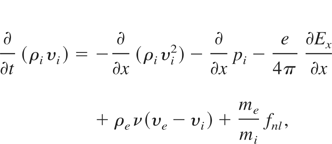
and the equations which allow us to take into account changes of the
temperature of ions and electrons (conservation of energy)
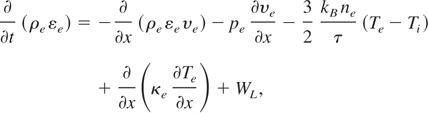
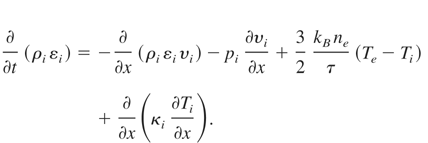
It was assumed that equations of state for these two fluids are
pe =
kBTe
ρe
/me,pi =
kBTi
ρi /mi (ideal
gas), where kB is the Boltzman constant and
electron and ion mass are me and
mi, respectively. As
εe is internal energy of electrons and
εi is energy of ions, we can replace these
quantities with temperatures using εe =
3/2kBTe
/me for electrons, and
εI =
3/2kBTi
/mi for ions. The quantities ν,
t, and WL are the collision
frequency, the temperature equipartition time, and the density of electron
heating power by laser absorption in plasma. The formulas for
κe and κi which are
thermal conductivities for the electron and ion fluids, respectively, must
be known.
To describe the Coulomb interaction between the two charged fluids,
which play the most crucial role in the ion current appearance, Poisson
equation was solved
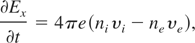
where Ex is the electric field in the
x-direction, ni and ne are the electron and ion
number densities, respectively.
To find non-linear ponderomotive force
(fNL = 1/cj ×
H) in the x-direction (fNL)
and the density of electron heating power
(WL), the electromagnetic wave equations in
plasma were solved
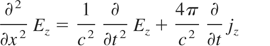
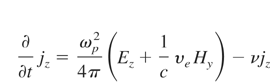
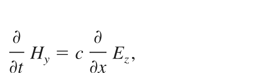
where Ez and
Hy, are electric and magnetic fields of laser
light and jz is a current in the z-direction. The impact
of electron motion in electric field of light wave on the collision
frequency ν, was taken into account. The equations of the model were
solved basing on the Lax method.
4. NUMERICAL TOOL FOR ESTIMATING OF THE
RIPPLING EFFECT
In order to estimate level of rippling effect and results of smoothing
an especial numerical tool based on the multilayers stack theory was
created.
The main idea of the method is simple:
- the region of plasma is divided into many layers of Δx
width (Δx is equal space step used in main simulating
program);
- within each layer refractive index is constant and is dependent on
collision frequency ν, plasma frequency ωp,
and laser pulse frequency ω;
- the laser pulse propagating through such a stack is reflected and
the level of reflection can be used as an indicator of
rippling.
For the derivation of main equations for multilayers method phase
relationship between electric E, and magnetic H fields
on the layer's border was taken into consideration (Fig. 1).
The idea of multilayers method of rippling evaluation.
The values for E and H evaluated on the first border
were used for evaluating such values on the next border and so on.
The main relations used in the method are described below:
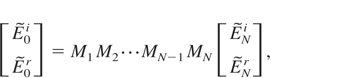
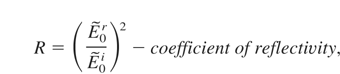
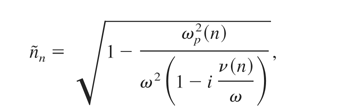
where
The example of correlation between plasma profile and refractive
coefficient is shown in Figure 2. Analyzing the
data in Figure 2, we can see that for plasma
block width of 2.5 μm reflectivity coefficient is equal to about 18%,
but for the width of 5 μm this value reach 62%. For ion density
profile without rippling, reflectivity coefficients are equal about 0% for
the width of 2.5 μm and 5 μm (Fig.
3).
Reflection of laser beam from plasma region as a function of the
distance and ion density profile. T = 1.2 ps, I =
1016 W/cm2, τ1/2 = 1 ps,
λ = 1.06 μm.
Reflection of laser beam from plasma region as a function of the
distance and ion density profile for time t = 0.6 ps since start
of interaction. I = 1016 W/cm2,
τ1/2 = 1 ps, λ = 1.06 μm.
A characteristic 100% reflection for plasma 13.5 μm wide is a
result of reflection from critical density region
ncr.
5. RESULTS AND DISCUSSION
The numerical calculations were performed for 20 μm hydrogen,
inhomogeneous plasma layer of initial density increasing in the direction
of the laser beam propagation. Linear plasma density profile described by
the function n(x) = (0.04x +
0.5)ncr, where
ncr—critical density,
x—distance from plasma face in μm was taken into
consideration. The mentioned density profile was preceded by short 1
μm plasma layer with a steeper density profile in order to improve
numerical stability (Fig. 3). The computations
were made for two laser intensities 1016 W/cm2
and 1017 W/cm2. For each intensity one wave,
three waves, and five waves cases of interaction with plasma were analyzed
(Table 1). In the case of multi waves, the total
maximum amplitude of electric E and magnetic H
components for waves was equal to the maximum amplitude E and
H for one wave case. The parameter “relative intensity of
laser beam” describes the relation between total intensity (not
maximum intensity) of the laser pulse used during computations, relatively
to the total intensity of one wave case. It should be noticed that this
relation is constant and independent of shift Δω, see Figure 4. The decrease in the total intensity in the
function of the wave's quantity is a result of interference between
multi wave's elements in laser pulse. Results for intensity
1016 W/cm2 are presented in Figure 5, Figure 6, Figure 7, and Figure 8.
Parameters of laser beams used during computations
Shapes of the laser pulse intensity for frequency shift between waves:
1.0% of ω0 (left figure) and 2% of ω0
(right figure).
Evolution of ion density profile (left figure) and reflection of laser
beam from plasma region (right figure) as a function of distance and
interaction time for one wave. I = 1016
W/cm2, τL = 1 ps, λ = 1.06
μm.
Evolution of ion density profile (left figure) and reflection of laser
beam from plasma region (right figure) as a function of distance and
interaction time for three waves of Δω = 0.5% ω0.
I = 1016 W/cm2,
τL = 1 ps, λ = 1.06 μm.
Evolution of ion density profile (left figure) and reflection of laser
beam from plasma region (right figure) as a function of distance and
interaction time for five waves of Δω = 1.0% ω0.
I = 1016 W/cm2,
τL = 1 ps, λ = 1.06 μm.
Evolution of the ion velocity profile for three waves (left figure)
and for five waves (right figure), results for 2 ps after the start of
interaction. I = 1016 W/cm2,
τL = 1 ps, λ = 1.06 μm.
Basing on the figures presented above we observed that for maximum of
laser pulse intensity 1016 W/cm2, differences
between interaction with plasma for one wave and multi-waves beams gives,
for maximum ion velocity, very similar results in both directions of the
plasma block propagation. Such an effect may be a surprise when we
remember the fact that total intensity of the pulse in the cases of three
and five waves is much smaller than in the case of one wave Figure 4. The main reason for the observed phenomena
is only one, the smoothing of rippling effect. The most reduction of
rippling amplitude was observed for frequency shift Δω = 0.5%
ω0 (three waves) and for Δω = 1.0%
ω0 (five waves). The mentioned amplitudes were decreased 3
times and 5 times, respectively. This fact was theoretically proved by
Glowacz et al. (2006).
Similar relations were observed for higher pulse intensity I
= 1017 W/cm2, Figure
9, Figure 10, Figure
11, and Figure 12, but for this example,
an advantageous influence of smoothing was much more distinct and maximum
values of ion velocities were about 2.5–3.0 times greater than for
the case without smoothing.
Evolution of ion density profile (left figure) and reflection of laser
beam from plasma region (right figure) as a function of distance and
interaction time for one wave. I = 1017
W/cm2, τL = 1 ps, λ = 1.06
μm.
Evolution of ion density profile (left figure) and reflection of laser
beam from plasma region (right figure) as a function of distance and
interaction time for three waves of Δω = 0.5% ω0.
I = 1017 W/cm2,
τL = 1 ps, λ = 1.06 μm.
Evolution of ion density profile (left figure) and reflection of laser
beam from plasma region (right figure) as a function of distance and
interaction time for five waves of Δω = 1.0% ω0.
I = 1017 W/cm2,
τL = 1 ps, λ = 1.06 μm.
Evolution of the ion velocity profile for three waves (left figure)
and for five waves (right figure), results for 1.5 ps after the start of
interaction. I = 1017 W/cm2,
τL = 1 ps, λ = 1.06 μm
It must be necessarily said that the method analyzed in the paper,
which is well known for longer pulses can be successfully used to improve
of the interaction between short (<1 ps) laser pulses and plasma.
6. CONCLUSIONS
- Using of broad-band laser irradiation method for rippling smoothing
always lead to decreasing of the plasma reflection, particularly for early
times of laser beam-plasma interaction.
- The lower average power density for three waves and five waves
methods of smoothing in relation to one wave case (33% for 3 waves, 20%
for 5 waves) does not cause of decreasing of ion velocity (this fact
confirm negative role of rippling for energy exchanging between laser beam
and plasma).
- For both intensities of laser beam, took into consideration
(1016 W/cm2 and 1017
W/cm2) optimal values of frequency shift for three waves
and five waves methods are established. For three waves smoothing optimal
value is for Δω ≈ 0.5%, but for five waves such value is for
Δω ≈ 1.0%.
- For the case of optimal smoothing, amplitude of rippling is
suppressed about 3 times, relatively to the case without smoothing.
- Mentioned above broad-band method is a good tool for smoothing of
rippling for short pulse (1 ps) and high-energy laser-beam interaction
with plasma.
ACKNOWLEDGMENTS
This work was supported in part by the State Committee for Scientific
Research (KBN), Poland under Grant No. 1 PO3B 043 26 and by a grant for a
Visiting Scientist by the University of Western Sydney, Australia.
