1. INTRODUCTION
Interaction processes of ion beam or cluster with matter are important for the applications in basic and applied physics (Patel et al., Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price and Ruhl2003; Brambrink et al., Reference Brambrink, Roth, Blazevic and Schlegel2006; Tahir et al., Reference Tahir, Schmidt, Shutov, Lomonosov, Piriz, Hoffmann, Deutsch and Fortov2009a), laboratory accelerator (Tahir et al., Reference Tahir, Spiller, Shutov, Lomonosov, Piriz, Redmer, Hoffmann, Fortov, Deutsch and Bock2009b), inertial confinement fusion (ICF) (Deutsch, Reference Deutsch1986; Deutsch et al., Reference Deutsch, Maynard, Bimbot, Gardes, Dellanegra, Dumail, Kubica, Richard, River, Sernagean, Fleurier, Sanba, Hoffmann, Weyrich and Wahl1989; Hora, Reference Hora2007; Hoffmann, Reference Hoffmann2008), astrophysical processes (Nettelmann et al., Reference Nettelmann, Holst, Kietzmann, French, Redmer and Blaschke2008), heavy ion beam research (Hoffmann et al., Reference Hoffmann, Tahir, Udreal, Rosmej, Meister, Varentsov, Roth, Schaumann, Frank, Blažević, Ling, Hug, Menzel, Hessling, Harres, Günther, El-Moussatil, Schumacher and Imran2010; Stöckl et al., Reference Stöckl, Frankenheim, Roth, Suß, Wetzler, Seelig, Kulish, Dornik, Laux, Spiller, Stetter, Stöwe, Jacoby and Hoffmann1996, Tahir et al. Reference Tahir, Kim, Matvechev, Ostrik, Lomonosov, Piriz, Cela and Hoffmann2007), and high energy density physics (HEDP) (Tahir et al., Reference Tahir, Deutsch, Fortov, Gryaznov, Hoffmann, Kulish, Lomonosov, Mintsev, Ni, Nikolaev, Piriz, Shilkin, Spiller, Shutov, Temporal, Ternovoi, Udrea and Varentsov2005; Nellis, Reference Nellis2006; Hoffmann et al., Reference Hoffmann, Fortov, Kuster, Mintsev, Sharkov, Tahir, Udrea, Varentsov and Weyrich2009). HEDP is understood to be the thermodynamic regime where the energy density exceeds 1011 J/m3 or equivalent pressure of 1 Mbar and above. Pioneering experiments of beam-matter interactions (Deutsch et al., Reference Deutsch, Maynard, Bimbot, Gardes, Dellanegra, Dumail, Kubica, Richard, River, Sernagean, Fleurier, Sanba, Hoffmann, Weyrich and Wahl1989) have been conducted to investigate the stopping power for hydrogen plasma, which have demonstrated that the stopping power can increase with the increasing ionization of plasma due to the free electrons interacting with beam ions. It will be shown very soon that intense clusters may be of considerable potential interest for driving an ICF (Deutsch, Reference Deutsch1992). Using clusters as a ICF driver, can break through the space-charge limit of ion beam, which is helpful to achieve high heating effect. Recently, several attempts have been made to investigate the beam-matter interactions involving heavy ion (Zhao et al., Reference Zhao, Xu, Zhao, Xia, Jin, Ma, Liu, Yang, Zhang, Wang, Li, Zhao, Zhan, Xu, Zhao, Li and Chen2009; Hoffmann et al., Reference Hoffmann, Tahir, Udreal, Rosmej, Meister, Varentsov, Roth, Schaumann, Frank, Blažević, Ling, Hug, Menzel, Hessling, Harres, Günther, El-Moussatil, Schumacher and Imran2010), proton (Patel et al., Reference Patel, Mackinnon, Key, Cowan, Foord, Allen, Price and Ruhl2003, Tahir et al., Reference Tahir, Schmidt, Shutov, Lomonosov, Piriz, Hoffmann, Deutsch and Fortov2009a) and laser beams (Zhao et al., Reference Zhao and Shin2012). In particular, ICF is a promising scheme, where a target matter can be irradiated by intense ion beams or clusters, and be transformed into a plasma of high density and high temperature which can initiate fusion reactions (Deutsch, Reference Deutsch1992; Tahir et al., Reference Tahir, Deutsch, Fortov, Gryaznov, Hoffmann, Kulish, Lomonosov, Mintsev, Ni, Nikolaev, Piriz, Shilkin, Spiller, Shutov, Temporal, Ternovoi, Udrea and Varentsov2005).
The basic properties of interactions between ions and matter, which play an essential role in the above scenario, have been encouraged to be explored thoroughly. The evaluations of target temperature and density are an ideal tool to investigate these interactions for ion beams or clusters immersed in a target. It is expected in such studies that target properties would be influenced significantly by the modulation of beam or cluster parameters such as particle energy, total number of particles per beam, and focal spot size. These beam parameters will be available at the new powerful heavy ion synchrotron, SIS100, at GSI Darmstadt, which will deliver strongly bunched intense beams and clusters of all stable ion species from protons up to uranium with particle energies a few MeV-GeV/u (Tahir et al., Reference Tahir, Schmidt, Shutov, Lomonosov, Piriz, Hoffmann, Deutsch and Fortov2009a, Reference Tahir, Shutov, Piriz, Lomonosov, Deutsch, Spiller and Stöhlker2011). These intense ion beams and clusters present a promising source for volumetric heating and bring up unique capabilities for HEDP. In this field, one of the special interests is warm dense matter (WDM) research, since the accelerator technology has improved sufficiently to provide intense ion beams and clusters to heat samples of target and reach the regime of WDM. WDM is the region in temperature (several eV) and density that can be described as strongly coupled plasma. The importance of WDM arises from its wide occurrence, namely planetary science, cold star physics, and all plasma production devices, which start from cold dense matter.
In a strong coupling plasma considering nonlinear effects, the interaction processes of ions with matter have been simulated by employing various methods, such as particle-in-cell (PIC) and molecular-dynamics (MD) (Zwicknagel et al., Reference Zwicknagel, Toepffer and Reinhard1999; Hu et al., Reference Hu, Song, Mišković and Wang2011, Reference Hu, Song and Wang2012). In particular, quantum hydrodynamic (QHD) model has been developed by solving the nonlinear Schördinger-Poisson or the Wigner-Poisson kinetic models, which can be devoted to studying the properties of strongly coupled plasmas. Large number of calculations have been carried out by using the QHD model since the use of this theory was introduced (Chen et al., Reference Chen, Cockburn, Gardner and Jerome1995; Haas et al., Reference Haas, Manfredi and Feix2000; Manfredi and Haas, Reference Manfredi and Haas2001), due to the advantages that the QHD equations are quite simple for numerical studies and have a straightforward interpretation in terms of fluid quantities that are employed in classical physics. In our previous work (Zhang et al., Reference Zhang, Song and Wang2011b), we have simulated the wake potential and energy loss of a test charge propagating in a one-dimensional (1D) solid target, by using the 1D QHD theory. However, the QHD theory has not been applied to examine an ion cluster interacting with a two-dimensional (2D) solid target so far.
The aim of this paper is to extend our previous work (Zhang et al., Reference Zhang, Song and Wang2011b) to a 2D case with an ion cluster interaction, moreover, the energy-balance equation is considered in this work. The 2D QHD approach will be employed to analyze the isochoric heating (i.e., heating at constant volume) of aluminum solid target under an ion cluster interaction, which can heat solid density material to warm dense states on a picosecond time scale. We shall show how the temperature and density of the target are affected by the modulation of cluster properties and how the WDM is generated from a cold target. The nonlinear QHD equations will be solved by employing the flux-corrected-transport (FCT) method (Boris et al., Reference Boris, Landsberg, Oran and Gardner1993), which has proven to be an accurate and easy to use algorithm to solve nonlinear time-dependent conservative equations of hydrodynamics. This paper is organized as follows. In Section 2, the nonlinear 2D QHD formalisms coupled with the Poisson's equation, are presented. In Section 3, we show numerical results of the temperature and density of the target. Finally, a short summary is given in Section 4. Gauss units will be adopted throughout the paper except specific definition.
2. QUANTUM HYDRODYNAMIC MODEL
We consider a Gaussian proton cluster of density profile n c (z, r, t) = n c0exp(−r 2/r c2 − (z − V ct)2/l c2) with cluster radius r c and cluster half-length l c, propagating with constant velocity 
$V_c=\sqrt {2E_{cp} /m_{cp} } $ through a solid aluminum target along the z axis. Here, m cp is the proton mass and E cp is the proton energy. The total number of protons N cp within cluster is N cp = 4π ∫0l c ∫0r cn c (z, r, t) rdrdz, functions of n c0, r c, and l c. Note that the total number and Gaussian distribution of protons within cluster are unvaried with time t evaluation. We treat the valence electrons in the target as free electrons with an equilibrium density n 0 = 7.829 × 10+23 cm−3, which is aluminum solid density, immersed in a uniform background of motionless ions. The electron dynamics can be analyzed by a collective-stimulated interaction model, that is, the transmission of the cluster ions can cause dynamics polarization effect in the target.
The simulation technique is the 2D QHD model with the electron velocity field ue (z, r, t), density n e (z, r, t), and energy density W e (z, r, t) by the continuity equation
$$\displaystyle{{\partial n_e } \over {\partial t}}+\nabla \cdot \left({n_e {\bf u}_e } \right)=0\comma \;$$the momentum-balance equation
$$\eqalign { & \displaystyle{{\partial {\bf u}_e } \over {\partial t}} +\left({{\bf u}_e \cdot \nabla } \right){\bf u}_e=\displaystyle{e \over {m_e }}\nabla \Phi - \displaystyle{{\nabla P_e } \over {m_e n_e }} \cr & \quad +\displaystyle{{\hbar ^2 } \over {2m_e^2 }}\nabla \Bigg( \displaystyle{1 \over {\sqrt {n_e } }}\nabla ^2 \sqrt {n_e } \Bigg) - {\rm \gamma} {\bf u}_e\comma \; } $$and the energy-balance equation (Chen et al., Reference Chen, Cockburn, Gardner and Jerome1995)
$$\eqalign {& \displaystyle{{\partial W_e } \over {\partial t}}+\nabla \cdot \lpar W_e {\bf u}_e \rpar =en_e {\bf u}_e \cdot \nabla \Phi - \nabla \cdot \lpar {\bf u}_e P_e \rpar \cr & \quad - \nabla \cdot {\bf q}_e - \displaystyle{{W_e - {\textstyle{3 \over 2}}n_e T_e } \over {{\rm \tau} _w }}\comma \; }$$
with 
$W_e={\textstyle{3 \over 2}}n_e T_e+{\textstyle{1 \over 2}}m_e n_e u_e^2 - {\textstyle{{\hbar} ^2 n_e } \over {24m_e }}\nabla ^2\, \log\lpar n_e \rpar +O\lpar \hbar ^4 \rpar $. The above equations are closed by adding Poisson's equation
$$\nabla ^2 \Phi=4{\rm \pi} e\lpar n_e - n_0 - Z_1 n_c \rpar .$$
Here, 
$\nabla={\textstyle{\partial \over {\partial r}}}\,{\bf e}_r+{\textstyle{\partial \over {\partial z}}}\,{\bf e}_z $, m e is the electron mass, e is the elementary charge, Φ is the total electric potential, qe, T e, and P e are the electron heat flux, temperature and pressure, respectively, γ and τw are the frictional coefficients with τw = 2γ. In particular, the electron pressure P e can be calculated by finite temperature Thomas-Fermi theory (More et al., Reference More, Warren, Young and Zimmerman1988) and the heat flux is specified by Fourier's law qe = −κ ∇ T e (Chen et al., Reference Chen, Cockburn, Gardner and Jerome1995) with thermal conductivity κ. In the right-hand side, the second and third terms of Eq. (2) are regarded as the quantum effects, and the last terms of Eqs. (2) and (3) are the frictional forces with γ and τw obtained from our previous work (Zhang et al., Reference Zhang, Song and Wang2011a).
The above Eqs. (1)–(4) involve a self-consistent determination of the electron density, velocity, and temperature, and the total electric field E =−∇Φ with the components E r and E z. The FCT method is adopted to numerically solve Eqs. (1)–(3) by split-time integration from the initial time t = 0 when the values of all quantities are known. The Poisson's equation is solved by the successive over relaxation (SOR) method.
In the following section, we obtain the numerical values of the density and temperature of the target under the effect of a Gaussian proton cluster. In the simulation, n c0 = n 0 × 10−9 and the cluster is projected from (z = 0, r = 0) at t = 0. Our numerical results are obtained for solid aluminum with initial solid density n 0 and initial temperature T e = 0 eV.
3. NUMERICAL RESULTS
Figure 1 show the density as functions of r and z at 5 ps Figure 1a and 10 ps Figure 1b for E cp = 20 MeV, and at 5 ps Figure 1c and 10 ps Figure 1d for E cp = 10 MeV. Here, r c = 3 µm and l c = 15 µm. The density demonstrates a clear time and space variations and wake effects are generated behind the cluster. A comparison between Figuers 1a and 1b shows that the maximum density is almost unchanged with the cluster penetration time. As the cluster penetrates deeper into the target, the perturbed density region becomes larger. When E cp = 20 MeV in Figures 1a–b, the range of the cluster is longer, while the maximum density is smaller, in comparison with that for E cp = 10 MeV in Figures 1c–1d. The perturbed density decreases and tends to reach an initial equilibrium value with the increasing distance behind the cluster.
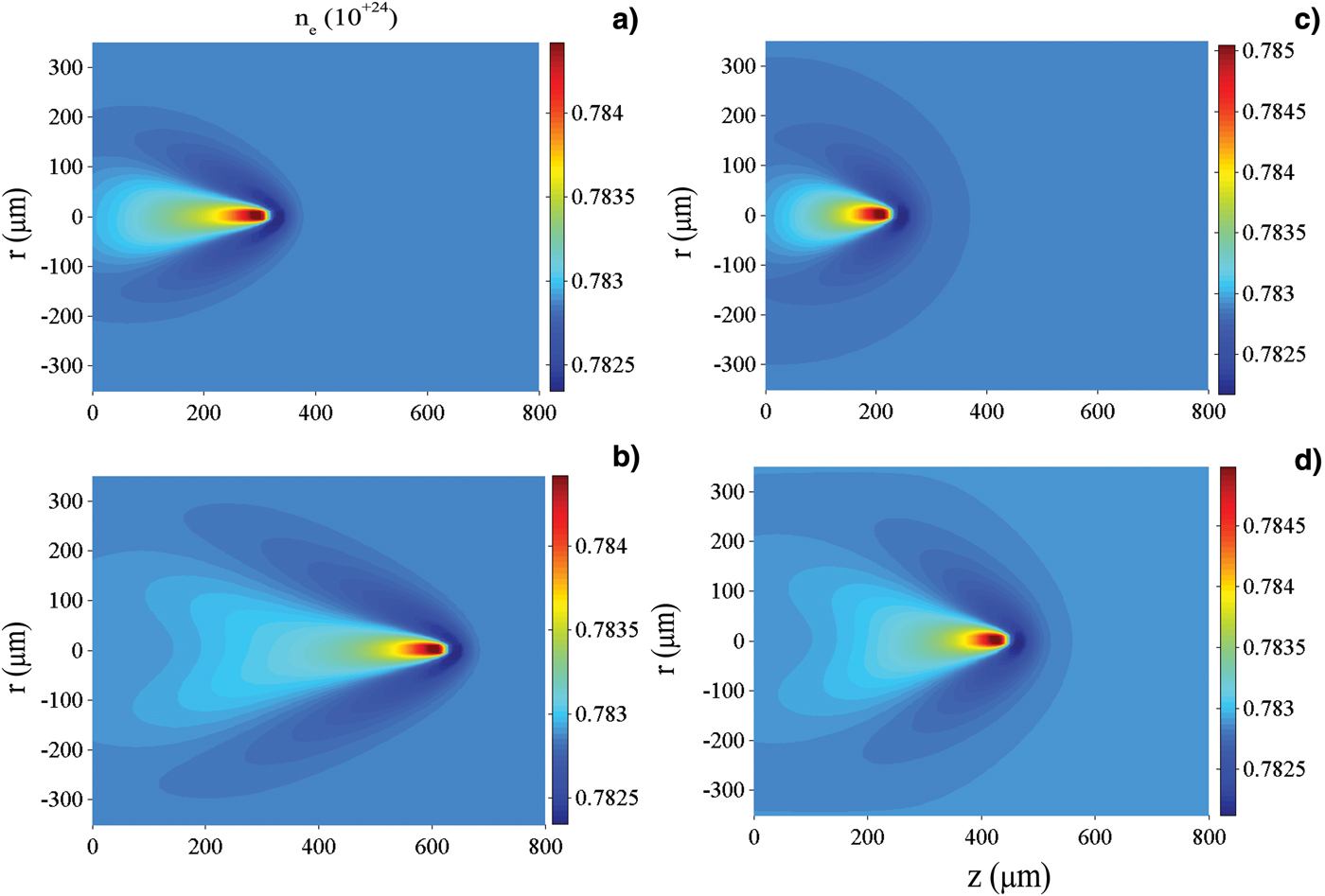
Fig. 1. (Color online) The density at 5 ps (a) and 10 ps (b) for E cp = 20 MeV, and at 5 ps (c) and 10 ps (d) for E cp = 10 MeV. Here, r c = 3 µm and l c = 15 µm.
Temperature corresponding to Figures 1a–1d is shown in Figures 2a–2d. Cluster protons impinging on the target deposit their energy in the target that leads to an increase in the temperature. Thus the spatial profile of the temperature is similar to the Gaussian distribution of the cluster. In the cluster heated region, temperature of 0.6 ≤ T e ≤ 1 eV is obtained in Figures 2a–2b and that of 1 ≤ T e ≤ 1.5 eV is obtained in Figures 2c–2d, where WDM is generated. The WDM temperature range is roughly T e = 1.0–20 eV for aluminum. As the cluster transmission time increases, a larger volume of the target has been heated. When E cp = 20 MeV in Figures 2a–2b, the range of the cluster is longer and the heated region is larger, while the maximum temperature is smaller, in comparison with those for E cp = 10 MeV in Figures 2c–2d. Moreover, more uniform temperature is obtained in Figs. 2(a-b), as compared to that shown in Figures 2c–2d. Note that nearly uniform temperature of several eV is achieved in the cluster heated region and the target can be converted into WDM on a picosecond time scale, which is important for the study of HEDP and ICF research.
Fig. 2. (Color online) The temperature at 5 ps (a) and 10 ps (b) for E cp = 20 MeV, and at 5 ps (c) and 10 ps (d) for E cp = 10 MeV. Here, r c = 3 µm and l c = 15 µm.
To further examine the influence of the cluster parameters on the density, we present in Figures 3a–3c the density as functions of r and z with r c = 1 µm, l c = 10 µm Figure 3a, r c = 3 µm, l c = 15 µm Figure 3b and r c = 6 µm, l c = 20 µm Figure 3c. Here, E cp = 20 MeV and t = 10 ps. In Figures 3a–3b the maximum density decreases with decreasing r c and l c due to reduction in n c that has a direct ratio relation with r c and l c.
Fig. 3. (Color online) The density with r c = 1 µm, l c = 10 µm (a), r c = 3 µm, l c = 15 µm (b) and r c = 6 µm, l c = 20μm (c). Here, E cp = 20 MeV and t = 10 ps.
Temperature corresponding to Figures 3a–3c, is presented in Figures 4a–4c. It is clearly seen in Figures 4a–4c where the cluster heated volume becomes larger in radial direction and the maximum temperature increases with increasing r c and l c. The temperature exhibits a nearly uniform distribution in the cluster heated region, which has values of T e = 0.4 ~ 2 eV. Moreover, the maximum temperature (2 eV) is in favor of important experiments on HEDP.
Fig. 4. (Color online) The temperature with r c = 1 µm, l c = 10 µm (a), r c = 3 µm, l c = 15 µm (b) and r c = 6 µm, l c = 20 µm (c). Here, E cp = 20 MeV and t = 10 ps.
The density and temperature are significantly impacted by the cluster properties, as a result, such a influence is also shown in the total electric field. Corresponding to Figure 3b and Figure 3c, Figures 5a–5b and Figures 5c–5d show E r and E z as functions of r and z, with E rFigure 5a and E zFigure 5b for r c = 3 µm, l c = 15 µm and E rFigure 5c and E zFigure 5d for r c = 6 µm, l c = 20 µm. Here, E cp = 20 MeV and t = 10 ps. The total electric field is mainly determined by the Gaussian cluster, so the initial values E r = 0, E z = 0 are changed only at and around the cluster center, as shown in Figures 5a–5d. The volume of nonzero electric fields is smaller for a lower r c and l c due to reduction in n c. The spectrum of E r displays an antisymmetry, while E z is symmetric, with respect to the axis (r = 0).
Fig. 5. (Color online) E r (a) and E z (b) for r c = 3 µm, l c = 15 µm and E r (c) and E z (d) for r c = 6 µm, l c = 20 µm. Here, E cp = 20 MeV and t = 10 ps.
4. CONCLUSIONS
Numerical simulations of interaction of a Gaussian proton cluster with 2D aluminum solid target are carried out. 2D QHD model is employed for the heating of solid target. A full self-consistent treatment of this problem requires coupling of the QHD formalisms with the Poisson's equation. The density and temperature of the target and the total electric field, are calculated by solving the QHD equations and the Poisson's equation. The FCT method is adopted to numerically solve the nonlinear QHD equations. The Poisson's equation is solved by the SOR method. As the cluster penetrates into the target, a uniform temperature distribution is displayed in the cluster heated region. It is interesting to note that the target is heated to a few eV and a WDM matter is generated in the cluster heated region on a picosecond time scale. Therefore, one can access the very interesting but almost unexplored strongly coupled plasma state in this work.
In the near future, this work could be modified to consider interactions of an intense ion beam pulse with solid target by using double QHD model for beam and target particles, where high energy density (HED) matter can be generated. The developments of high-quality well-focused strongly bunched intense ion beams, from a facility of antiproton and ion research (FAIR) at GSI Darmstadt, can lead to generating samples of HED matter through isochoric and uniform heating of solid targets by such intense beams.
ACKNOWLEDGMENT
This work was supported by the National Basic Research Program of China (Grants No. 2010CB832901), Fundamental Research Funds for the Central Universities (Grant No. DUT10ZD111), National Natural Science Foundation of China (Grant No.10975028), and the Program for New Century Excellent Talents in University (NCET-08-0073).
