The numerical code and the laser and target parameters

In this paper, we investigate the acceleration of C, Cu or Pb ions by a multi-PW laser pulse with parameters corresponding to those of the ELI-NP lasers. The numerical simulations were performed using a fully electromagnetic, relativistic multi-dimensional (2D3V) PIC code (Domański et al., Reference Domański, Badziak and Jabłoński2017) extended with “on-line” calculations of the ionization levels of the target atoms and accelerated ions that are especially important for properly modeling the acceleration of medium-heavy and heavy ions that are not fully ionized by the laser-induced fields. For the laser intensities assumed in the simulations, tunnel ionization is the dominant mechanism of ionization of the considered atoms. For all ionization levels of these atoms, the Keldysh parameter is much smaller than 1 and the ionization energies are considerably smaller than the electron rest energy (Popov, Reference Popov2004; Kramida et al., Reference Kramida, Ralchenko and Reader2018). Under such conditions, the process of ionization of the target atoms could be described using the Ammosov-Delone-Krainov formula (Ammosov et al., Reference Ammosov, Delone and Krainov1986; Chen et al., Reference Chen, Cormier-Michel, Geddes, Bruhwiler, Yu, Esarey, Schroeder and Leemans2013), which was implemented to the numerical code.

The simulations were carried out for a 30 fs laser pulse with a wavelength of 0.8 µm and circular polarization, a peak intensity of 10²³ W/cm², and a beam width [full width at half maximum (FWHM)] d _L = 3 µm [these parameters correspond to a laser pulse energy of 220 J and are to be available at the ELI-Nuclear Physics infrastructure (Negoita et al., Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Balascuta, Cappuzzello, Cernaianu, Chen, Dancus, Freeman, Geissel, Ghenuche, Gizzi, Gobet, Gosselin, Gugiu, Higginson, D'Humieres, Ivan, Jaroszynski, Kar, Lamia, Leca, Neagu, Lanzalone, Meot, Mirfayzi, Mitu, Morel, Murphy, Petcu, Petrascu, Petrone, Raczka, Risca, Rotaru, Santos, Schumacher, Stutman, Tarisien, Tataru, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir2016; http://www.eli-laser.eu)]. The laser beam shape in space (along the y-axis) and time was described by a super-Gaussian function with a power index equal to 6. The laser pulse interacted with a flat carbon, copper or lead target with a thickness (L _T) equal to 100 nm, a transverse size of 16 µm and an atom density corresponding to a solid-state density (1.76 × 10²³ atoms/cm³ for carbon, 8.45 × 10²² atoms/cm³ for copper, and 3.30 × 10²² atoms/cm³ for lead). A pre-plasma with a density scale length of 20 nm and with a density shape described by an exponential function was placed in front of the target. The simulations were performed in the x, y space of dimensions 80 × 20 µm². The space and time steps were equal to 13.3 nm and 2.22 as, respectively. The number of ion macro-particles was assumed to be 4330800 (400 particles/cell) for C, 2165400 (200 particles/cell) for Cu and 1082700 (100 particles/cell) for Pb.

Ionizing properties of the generated ion beam

During the interaction of an ultra-intense laser beam with a solid target, the target atoms are ionized by a strong electric field of the laser beam. After the plasma has been produced, the ions created are additionally ionized by the strong electric field generated in the plasma as a result of the local imbalance between the positive charge of ions and the negative charge of the electrons surrounding the ions. In the considered case of ultra-relativistic laser intensities, the temperature of the plasma electrons is in the multi-MeV range (see further) and the electron mean free path is much longer than the target or the plasma size. As a result, the collisional ionization of the target atoms and the plasma ions by the electrons, as well as the electron–ion recombination, can be neglected.

Figure 1 presents the ionization spectra of ions, produced from the target made of C, Cu or Pb, at t = 100 fs, so at the late stage of the ion acceleration process (t > 3τ_L, where τ_L is the laser pulse duration). The carbon target is ionized to the highest possible charge state z = 6 and actually, only one C ion specie with z = 6 is accelerated. In the case of a medium-heavy (Cu) or heavy (Pb) target, many highly charged ion species are produced and accelerated, and the mean ionization level in the ion beam is Q _mean = 23.3 for the Cu beam, and Q _mean = 53.3 for the Pb beam.

Fig. 1. The ionization spectra of ions produced from the target made of carbon (a), copper (b) or lead (c) at the late stage of ion acceleration.

Figure 2 shows 2D spatial distributions of the ionization level in the ion beams generated from a C, Cu or Pb target at the late stage of ion acceleration. In the case of the C target, only ions with the charge state z = 6 occur both in the laser-irradiated and non-irradiated part of the target. In the beams of Cu and Pb ions, the spatial distribution of the ionization level is strongly inhomogeneous, with the highest ionization levels being observed in the central part of the beam. It is worth emphasizing that both the ionization spectrum and the spatial distribution of the ionization level in the beam change during the acceleration process. This causes the ion acceleration process to be complex, especially in the case of acceleration of medium-heavy and heavy ions.

Fig. 2. 2D spatial distributions of the ionization level in the ion beams generated from the target made of carbon (a), copper (b) or lead (c) at the late stage of ion acceleration.

Spatial characteristics of the ion beam and ion acceleration mechanisms

Both the spatial distribution of the density of ions and electrons in the generated ion beam, as well as the distributions of laser-induced electric fields in the plasma are an important source of information on ion acceleration mechanisms. Understanding these mechanisms is, in turn, crucial for developing methods to control the ion acceleration process and obtain parameters of the ion beam desirable for specific applications. Figure 3 presents 2D spatial profiles of the ion density (a, d), electron density (b, e), and the electric field accelerating ions E _x (c, f) at the early stage (t ~ τ_L) of the acceleration process for the C and Pb targets. At this stage, RPA is a dominant acceleration mechanism both for light and heavy ions, and in both cases, fairly dense and compact ion (plasma) bunches are accelerated along the laser beam axis. The ion densities in the bunches approach the densities of the solid targets from which the bunches are produced, and the accelerating fields reach extremely high values ~1 TV/cm.

Fig. 3. 2D spatial distributions of the ion density (a, d), electron density (b, e), and the electric field accelerating ions E _x (c, f) at the early stage of ion acceleration for the carbon (a, b, c) and lead (d, e, f) targets.

2D spatial profiles of the ion density (a, d), electron density (b, e), and the electric field accelerating ions E _x (c, f) at the late stage (t > 3τ_L) of ion acceleration are presented in Figure 4. At this stage, both light and heavy ions are accelerated by an electric field created by hot electrons moving far away from the ions. This field is strong enough (the field amplitude locally surpasses 100 GV/cm) not only to effectively accelerate the ions from the central region of the target irradiated by the laser beam but also to ionize the target atoms and accelerate the formed ions from the non-irradiated part of the target. This sheath acceleration (SA) mechanism results in a rather complex structure of the ion beam, though also in this case a relatively dense and compact ion (plasma) bunch accelerated along the laser beam axis can be observed. The ion acceleration mechanisms are even more clearly visible in Figure 5, where the spatial profiles of the ion density, the electron density, and the electric field accelerating ions E_x along the laser beam axis at the early (a,c) and late (b, d) stages of ion acceleration are shown. At the early stage, the RPA field clearly prevails over the SA field for both light and heavy ions. At the late stage, the ions are accelerated by the SA field, which is significantly weaker than the RPA field, however. As a result, most of the energy was delivered to the ion beam in the RPA stage. At the late stage of acceleration, some differences in the acceleration mechanisms of light and heavy ions can be observed. In the case of light ions, the Coulomb explosion of ions affects the acceleration process, while in the case of heavy ions this effect does not occur. The main reason for this seems to be the strong compression of the carbon plasma bunch in the RPA acceleration stage, which causes the electrons surrounding the carbons ions to be unable to shield the ions efficiently enough in the post-RPA stage when the radiation pressure that compressed the bunch is equal to zero.

Fig. 4. 2D spatial distributions of the ion density (a, d), electron density (b, e), and the electric field accelerating ions E _x (c, f) at the late stage of ion acceleration for the carbon (a, b, c), and lead (d, e, f) targets.

Fig. 5. Spatial profiles of the ion density, the electron density and the electric field accelerating ions, E _x, along the laser beam axis in the carbon (a, b) and lead (c, d) ion beams at the early (a, c) and late (b, d) stages of ion acceleration.

The ion energy spectra

The energy spectra of C, Cu, and Pb ions for the central (“useful”) part of the ion beam of diameter d _C = 2d _L = 6 µm and for the final stage of ion acceleration (t = 250 fs) are shown in Figure 6. For a better visualization of the structure of these spectra, they were presented using both the logarithmic scale and linear scale on the vertical axis. For all the ion beams considered, the spectra are broad, though their shapes are different. In the case of C and Cu ions, the two-peak structure in the high-energy range of the spectrum is clearly visible, while in the case of Pb ions, only a very flat and wide peak in the energy spectrum can be seen. In general, the complex structure of the spectra is a reflection of the complex spatial structure of the ion beam (see Fig. 4) and the contribution of the RPA and SA mechanisms to the ion acceleration process. In the case of medium-heavy (Cu) and heavy (Pb) ions, the main reason for the wide energy spectrum of these ions is the presence of many ion species with different q _i/m _i ratios in the ion beam (q _i is the ion charge and m _i is the ion mass), which results in different acceleration efficiencies of these ion species. In the case of the carbon ion beam, only one type of ion with z = 6 is actually accelerated, though there is an additional factor causing the broadening of the spectrum, namely the Coulomb explosion in the SA dominated acceleration stage. An additional factor causing the broadening of the spectrum that occurs in all the considered cases is the heterogeneity of the transverse distribution of the intensity in the laser beam.

Fig. 6. The energy spectra of C, Cu, and Pb ions for the central part of the ion beam with a diameter of d _C = 6 µm presented using the logarithmic scale (a) and the linear scale (b) on the vertical axis.

The absolute values of the maximum and mean energy of C, Cu, and Pb ions, as well as the ion energies per nucleon, calculated for the central part of the ion beam of d _C = 6 µm, are presented in the diagram in Fig. 7. The absolute values of the ion energies grow with the increase of the ion mass (the ion mass number) while the ion energies per nucleon decrease with the increase of the ion mass. The main reason for this decrease is a decrease in the average value of the q _i/m _i ratio in the ion beam with the growth in the ion mass, which the values for C, Cu, and Pb ions are equal to 0.5, 0.37, and 0.26, respectively. For all kinds of ions considered, the mean ion energies are in the multi-GeV range and the maximum energies reach into the tens of GeV.

Fig. 7. The absolute values of the maximum and mean energy o C, Cu, and Pb ions (a) and the ion energies per nucleon (b), calculated for the central part of the ion beam with d _C = 6 µm.

The number of accelerated ions and the laser-to-ions energy conversion efficiency

The total number of accelerated C, Cu, and Pb ions, and the number of high-energy (E _i > 1 GeV) ions for the central region of the ion beam (d _C = 6 µm) and for the whole beam, is shown in Figure 8. In turn, Figure 9 presents the laser-to-ions energy conversion efficiency for all the ions and the high-energy ions for the beam central region and for the whole beam. Both the number of accelerated ions and the laser-to-ions energy conversion efficiency decrease with an increase in the ion mass, though the decrease in the conversion efficiency is much smaller, as the energies of heavy ions are significantly higher than those of the light ions (Fig. 7). It can also be seen that most of the energy of the ion beam is concentrated in high-energy ions with GeV energies and the conversion efficiency is fairly high – above 10% for the central region and above 30% for the whole beam. It is significant that the energy accumulated in the whole beam is about three times higher than the energy contained in its central, most intense part, driven mainly by the RPA mechanism. This is due to the fact that, although the ions from outside the central region are less energetic, their number is nearly an order of magnitude higher than in the central region, and as a result, they carry most of the energy stored in the beam. This, in turn, means that most of the laser energy is transferred to the ion beam via an accelerating field created by hot electrons pushed out of the central region by laser-induced ponderomotive forces (see Fig. 4).

Fig. 8. The total number of accelerated C, Cu, and Pb ions and the number of high-energy (E _i > 1 GeV) ions for the central region of the ion beam with d _C = 6 µm (a) and for the whole beam (b).

Fig. 9. The laser-to-ions energy conversion efficiency for all the ions and the high-energy (E _i > 1 GeV) ions for the central region of the ion beam with d _C = 6 µm (a) and for the whole beam (b).

The ion beam fluence, intensity, and duration

Important parameters of ultra-intense ion beams are the ion fluence F _i (the number of ions per cm²), the ion energy fluence F _ie (measured in J/cm²), and the beam peak intensity I _i (measured in W/cm²), as well as the ion pulse duration and shape. Figure 10 presents the ion fluence and the ion energy fluence of the C, Cu, and Pb ion beams for all ions generated from the central region of the target (d _C = 6 µm), as well as the F _i and F _ie values for the high-energy ions with E _i > 1 GeV. The ion fluence decreases with an increase in the ion mass, while the ion energy fluence of the beam is almost independent of the ion mass since the reduction in the number of ions is compensated by the increase in their energy. Both the ion fluence and the ion energy fluence reach very high values (F _i > 10¹⁷ ions/cm², F _ie > 10⁸ J/cm²) hardly achievable in conventional RF-driven accelerators.

Fig. 10. The ion fluence and the ion energy fluence for all the ions (a) and the high-energy ions (b) accelerated in the central region of the C, Cu, and Pb beams.

The temporal shape, peak intensity, and duration of the ion pulse generated from the target made of C, Cu, or Pb and recorded at the distance of 30 µm behind the target, are shown in Figures 11 and 12. It can be seen that the peak intensity of the ion pulse decreases and the pulse duration increases, with an increase in the ion mass. Although the energy spectra of accelerated ions are broad, the ion pulse durations are very short, ~10–60 fs, since the spatial length of the main, most energetic ion bunch in the C, Cu or Pb ion beam is only a few μm, and the mean velocity of the bunch is very high >10¹⁰ cm/s. Peak intensities of the ion pulses reach extremely high values ~10²¹–10²² W/cm² because the ion bunches are dense and the ions in the bunch have high velocities and energies (the ion pulse intensity I _i = n _iv _iE _i, where n _i, v _i, and E _i are the ion density, velocity and energy, respectively). The demonstrated values of the ion pulse duration are by a factor of 10⁴–10⁵ shorter, and the peak intensities are by a factor of 10² higher than those attainable currently in conventional RF-driven ion accelerators. Also, peak powers of the ion pulses are very high and at the distance of 30 µm behind the target they reach values about 2.5 PW for the C ion beam, 0.5 PW for the Cu beam, and 0.4 PW for the Pb beam.

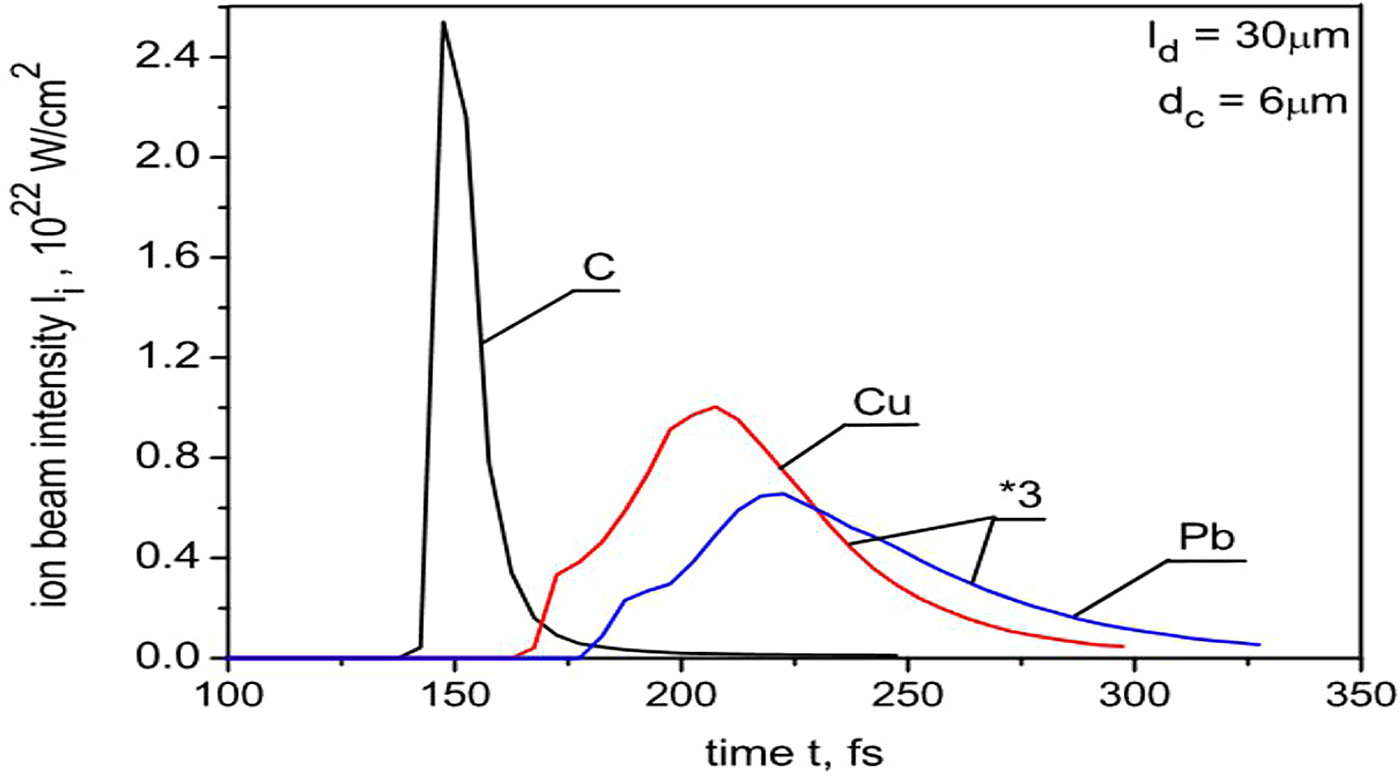
Fig. 11. The temporal shapes of ion pulses generated from the central region (d _C = 6 µm) of the carbon, copper or lead target recorded 30 µm behind the target.

Fig. 12. The peak intensity and duration of ion pulses generated from the central region (d _C = 6 µm) of the carbon, copper or lead target recorded 30 µm behind the target.

The angular divergence of the ion beam

Significant inhomogeneity of the charge density distribution in the ion beam (especially pronounced in the case of the Pb and Cu ion beams – Fig. 2) and the complex and non-uniform structure of the field accelerating ions in the post-RPA stage (Fig. 4) result in the distribution of ion velocities in the beam, in both axial and radial directions, also being inhomogeneous, and therefore the angular distribution of the beam intensity is fairly complex, with the effective angular divergence of the beam being significant. This is illustrated in Figure 13, where the angular distribution of beam intensity in the x–y plane and the effective (FWHM) angular divergence of the C, Cu, and Pb ion beams is shown. It can be seen that the angular distribution of the beam intensity essentially depends on the type of accelerated ions, and the angular divergence of the light ion beam is half the value of the angular divergence of medium-heavy and heavy ion beams. One of the reasons for this is the better uniformity of the charge density distribution in the light ion beam (Fig. 2). A relatively large angular divergence of the ion beam and the dispersion of the ions velocity cause that the intensity of the beam decreases quite rapidly with the increase of the distance from the laser-irradiated target, and achieving a high intensity of the ion beam is possible only at small (sub-millimetre) distances from the target. Thus, in ion beam–target interaction experiments in which a high ion beam intensity is desired, the distance between the laser-irradiated target and the beam-irradiated target should be as small as possible.

Fig. 13. The angular distribution of beam intensity in the x–y plane (a) as well as the peak intensity and the angular divergence (b) of the C, Cu, and Pb ion beams in this plane recorded in the maximum of the ion pulse at a distance of 30 µm behind the target.

The influence of radiation losses and other effects on the parameters of ultra-intense ion beams

Laser-driven ion acceleration at ultra-relativistic laser intensities can potentially be accompanied by the generation of ultra-relativistic electrons with the Lorenz factor γ >> 1 (electron energies of tens of MeV or higher), which can lose part of their energy due to synchrotron radiation, and these radiation losses (RL) can influence the ion acceleration process (e.g. Capdessus and McKenna, Reference Capdessus and McKenna2015; Tamburini et al., Reference Tamburini, Pegoraro, Di Piazza, Keitel and Macchi2010). It was shown, for example in Capdessus and McKenna (Reference Capdessus and McKenna2015), that the RL of ultra-relativistic electrons can significantly affect the acceleration of protons or deuterons driven by a laser pulse with an intensity of 10²³ W/cm², and can enhance or reduce the ion acceleration efficiency in dependence on the target areal density. However, as it was shown in Tamburini et al. (Reference Tamburini, Pegoraro, Di Piazza, Keitel and Macchi2010), the influence of RL on ion beam parameters significantly depends on the laser beam polarization, and for the circular polarization this influence can be small, even at very high laser intensities ~10²⁴ W/cm². In general, the influence of RL on the ion acceleration process depends on both the laser pulse and target parameters, and can significantly affect this process only if certain specific laser–target interaction conditions are met.

In order to check the possible influence of RL on the parameters of ultra-intense ion beams considered in this paper, we analyzed the energy spectra of electrons generated from C, Cu or Pb targets during the ion acceleration process. Figure 14 presents the energy spectra of fast electrons generated from the C, Cu, and Pb targets. In the case of medium-heavy (Cu) and heavy (Pb) targets, the mean electron energies are relatively small (2.6 MeV and 2.5 MeV, respectively) and the energy stored in ultra-relativistic electrons (of energy >50 MeV) is below 1% of the total electron energy. There are two reasons for such a small contribution of ultra-relativistic electrons in the electron energy balance. The first reason is the strong coupling of the vast majority of electrons with ions (Figs 3 and 4), resulting from the high charge state of Cu and Pb ions (Fig. 1), and the relatively small, non-relativistic mean velocities of these ions. The second reason is the circular polarization of the laser beam, which is much less effective in producing high-energy electrons than linear polarization (Macchi et al., Reference Macchi, Cattani, Liseykina and Cornalti2005; Reference Macchi, Borghesi and Passoni2013; Zheng et al., Reference Zheng, Wang, Yan, Tajina, Yu and He2012). Because the source of RL is ultra-relativistic electrons, the small total energy stored in these electrons means that a total energy loss due to synchrotron radiation is also small, so the effect of RL on parameters of the Cu and Pb ion beams should be negligible. The electrons generated from the light (C) target are more energetic than those generated from the heavier targets – the mean energies of these electrons are equal to about 12 MeV, and the energy stored in the ultra-relativistic electrons reaches several per cent of the total electron energy. Probable reasons for the observed differences between energies of electrons generated from the light and heavy targets are the smaller charge state of C ions and their higher velocities. Thus, in the case of the C target, the RL can be noticeable, and the effect of RL on the C ion energy spectrum, especially the maximum energy of C ions, can be noticeable as well. However, the effect of RL on the most important parameters of ultra-intense C ion beams, such as the beam intensity and fluence, the ion pulse duration, the ion bunch density and velocity is expected to be small, as in the case of Cu and Pb ion beams.

Fig. 14. The energy spectra of electrons generated from the central region (d _C = 6 µm) of the carbon, copper or lead target.

Another possible source of energy loss of accelerated ions, which was not taken into account in our investigations of ultra-intense ion beam generation, are hydrocarbon contaminants, usually occurring on the surfaces of solid targets, especially on metal targets. The protons from contaminants are accelerated by the sheath field created by hot electrons and when SA is a dominant mechanism of ion acceleration, the energy carried by protons can significantly decrease the laser energy converted to heavier ions. However, in the cases considered in our paper, most of the energy is delivered to the ion beam by the RPA mechanism (see the section Spatial characteristics of the ion beam and ion acceleration mechanisms), and especially the parameters of the dense ion bunch formed by RPA and accelerated along the laser beam axis are expected to be weakly influenced by proton contaminants. Since the parameters of this ion bunch determine the most important parameters of the ultra-intense ion pulse (the ion pulse fluence, intensity, duration, and mean energy), the effect of energy losses associated with the existence of contaminants on the ion pulse parameters is expected to be small. The influence of these losses on parameters of the heavy (thorium) ion beam driven by a femtosecond laser pulse with intensity 10²³ W/cm² was checked in (Domański and Badziak, Reference Domański and Badziak2018), where the PIC simulation of heavy ion generation from the 100 nm thorium target with the proton layer of a thickness of 26.6 nm and a density equal to 0.1 g/cm³, situated inside the target close to the target rear surface, was performed. The simulations showed a decrease in the maximum energy of heavy ions equal to 9%, and a negligible influence of the proton layer on the mean ion energy, intensity, and duration of the heavy ion beam. Since the laser and target parameters in this simulation were similar to those in our present work, it is reasonable to believe that the effect of hydrocarbon contaminants on parameters of ultra-intense ion beams investigated in this work will be small, at least in the case of Pb and Cu ion beams.

Therefore, we have reasons to believe that, in the cases considered in this paper, the impact of both radiation energy losses due to synchrotron radiation and energy losses resulting from the presence of hydrocarbon contaminants in the target on ion beam parameters of importance for potential applications of ultra-intense ion beams will be small.

HED physics

The HED state of matter is usually defined as a state in which the energy density is >10⁵ J/cm³ or, equivalently, the pressure is >1 Mbar (Drake, Reference Drake2006). The creation and examination of such states of matter are desirable for research in materials science, astrophysics, planetology, and ICF. HED states are routinely produced by high explosives, pulsed-power (Z-pinch) devices, high-peak-power lasers and intense particle beams (Drake, Reference Drake2006; Hoffmann et al., Reference Hoffmann, Fortov, Kuster, Mintsev, Sharkov, Tahir, Udrea, Varentsov and Weyrich2009; Sharkov et al., Reference Sharkov, Hoffmann, Golubev and Zhao2016). Particle beams, and especially ion beams, have a number of advantages in the creation of HED states, in particular: The possibility of deep penetration into the target; the ability to create HED states in practically any dense material; and the relatively good uniformity of the distribution of energy deposited in the material.

The key parameters characterizing an ion beam's ability to create HED states are the energy deposited per gram of matter (Sharkov et al., Reference Sharkov, Hoffmann, Golubev and Zhao2016): E _s = (1.6 × 10⁻¹⁹)(dE _i/dx)F _i [J/g] and the deposition power P _s = E _s/t _d, where dE _i/dx is the ion stopping power of the material, F _i is the ion fluence and t _d is the energy deposition time. To assess this ability for the ion beams considered in this paper, let us estimate the values of E _s and P _s for the case of the interaction of the Pb ion beam accelerated by the multi-PW laser considered in the paper with a carbon target. For a very rough estimate of these values, we assume that the stopping power for the laser-driven ions characterized by the mean ion energy is similar to the stopping power of ions with the same mean energy produced in a conventional accelerator. Taking into account the Pb ion beam parameters: The mean ion energy < E _i > ≈ 40 MeV/nucleon, F _i ≈ 1.2 × 10¹⁷ cm⁻², τ_i ≈ 60 fs (see Figs 7, 10 and 12), the stopping power for 40-MeV Pb ions in carbon dE _i/dx ≈ 60 MeV/(mg/cm²) (Paul, Reference Paul and Natanasabapathi2012) and assuming t _d ≈ τ_I, we obtain: E _s ≈ 1.2 GJ/g, P _s ≈ 2 × 10²² W/g. For a comparison, the E _s and P _s values predicted for heavy ion beams produced by very big RF-driven heavy ion accelerators, such as the Facility for Antiproton and Ion Research (FAIR) accelerator (being built in GSI, Darmstadt) or the High Intensity heavy ion Accelerator Facility (HIAF) accelerator (designed in the Institute of Modern Physics, Lanzhou), approach ~0.1 MJ/g and ~10¹² W/g for FAIR and ~1 MJ/g and 10¹³ W/g for HIAF (assuming t _d ~ τ_i ~ 100 ns), respectively (Sharkov et al., Reference Sharkov, Hoffmann, Golubev and Zhao2016). Thus, the values E _s and P _s estimated for the heavy ion beam driven by a multi-PW laser are by many orders of magnitude higher than those achievable for the biggest RF-driven accelerators. It should be emphasized, however, that the stopping power values for beams of such high intensities and densities as demonstrated in our work are, in fact, unknown, and the collective effects expected at such high ion beam densities can significantly modify the values predicted by the Bethe-Bloch equation and used for the above estimates. In addition to the very high intensities/fluencies and densities of ultra-intense ion beams driven by a multi-PW laser, an important parameter determining the interaction of such a beam with matter is the very short (sub-picosecond) duration of the beam. This means that the time of depositing energy in the material is much shorter than the time period in which the material parameters change due to its hydrodynamic motion and we deal with the isochoric heating of the material. Such an isochoric regime of beam–target interaction is hardly achievable with ion beams produced by RF-driven accelerators due to long (ns or longer) durations of these beams. Thus, the unique parameters of ultra-intense laser-driven ion beams make it possible to explore essentially new regimes of ion beam–matter interaction, not attainable or barely attainable for conventional accelerators.

Nuclear physics

The extremely high intensities and very short durations of ion beams driven by a multi-PW laser render nuclear physics research possible with unusual efficiency of the ion beam–target interaction and in principally new time scales. As a result, some low-cross-section and/or transient nuclear reactions that would be hardly observable using ion beams produced by a conventional RF-driven accelerator could be feasible to be investigated. Examples are the nuclear phenomena planned to be studied within the research programme of the ELI-Nuclear Physics infrastructure. One of the topics in this program, which is particularly important for understanding the nature of the creation of heavy elements in the universe, is to study the production of neutron-rich heavy nuclei by a reaction mechanism called fission–fusion, using thorium (Th) ions accelerated by a multi-PW laser (Negoita et al., Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Balascuta, Cappuzzello, Cernaianu, Chen, Dancus, Freeman, Geissel, Ghenuche, Gizzi, Gobet, Gosselin, Gugiu, Higginson, D'Humieres, Ivan, Jaroszynski, Kar, Lamia, Leca, Neagu, Lanzalone, Meot, Mirfayzi, Mitu, Morel, Murphy, Petcu, Petrascu, Petrone, Raczka, Risca, Rotaru, Santos, Schumacher, Stutman, Tarisien, Tataru, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir2016). The creation of a sufficiently large, measurable amount of the neutron-rich heavy nuclei in this way requires, however, thorium ion beams with very high ion fluencies F _i and beam intensities I _i that are unachievable in RF-driven accelerators. In particular, the ion beam parameters should be as follows: A mean energy of thorium ions of 1.6 GeV, F _i ~10¹⁸ cm−2, I _i ~ 10²⁰ W/cm2 and the total number of thorium ions Ni ~ 10¹¹ (Negoita et al., Reference Negoita, Roth, Thirolf, Tudisco, Hannachi, Moustaizis, Pomerantz, McKenna, Fuchs, Sphor, Acbas, Anzalone, Audebert, Balascuta, Cappuzzello, Cernaianu, Chen, Dancus, Freeman, Geissel, Ghenuche, Gizzi, Gobet, Gosselin, Gugiu, Higginson, D'Humieres, Ivan, Jaroszynski, Kar, Lamia, Leca, Neagu, Lanzalone, Meot, Mirfayzi, Mitu, Morel, Murphy, Petcu, Petrascu, Petrone, Raczka, Risca, Rotaru, Santos, Schumacher, Stutman, Tarisien, Tataru, Tatulea, Turcu, Versteegen, Ursescu, Gales and Zamfir2016). Our numerical investigation into the acceleration of lead ions presented above (the atomic numbers and masses of Pb and Th ions are very similar), as well as the studies presented in (Domański and Badziak, Reference Domański and Badziak2018), showed that these ion beam parameters are within the reach of a laser accelerator of heavy ions driven by the ELI-NP multi-PW laser.

Inertial confinement fusion

An important potential application of ultra-intense ion beams is ICF. In the so-called fast ignition (FI) scenario of ICF, a deuterium-tritium (DT) fuel compressed by high-energy ns laser or X-ray beams is ignited by an ultra-intense particle (electron or ion) beam (Fernandez et al., Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin2014). The FI approach has substantial advantages over conventional, central-hot-spot ICF, in particular:Higher energy gain, lower required driver energy, lower susceptibility to hydrodynamic instabilities and flexibility in using different compression drivers. In the case of using light or moderate-heavy ion beams for high-gain DT fusion in the FI approach, the required parameters of the ion beam are estimated to be as follows (Davis et al., Reference Davis, Petrov and Mehlhorn2011; Fernandez et al., Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin2014): The mean ion energy ~10–50 MeV/nucleon, the beam intensity ~10²⁰ W/cm², the ion pulse duration ~ps, and a total beam energy of ~10–20 kJ. Although the required beam energy is attainable only using 100 kJ-class short-pulse laser drivers, the remaining beam parameters are well within the reach of multi-PW laser drivers such as ELI lasers. As demonstrated above, the mean ion energies and beam intensities of the ion beams driven by the multi-PW ELI laser can be significantly higher and the beam duration can be much shorter than required. Moreover, the last two parameters can be simply controlled by changing the distance between the ion source and the ion beam-irradiated target. Thus, these beams can be quite effectively applied in various areas of fundamental research into the FI approach to ICF.

Research challenges

Although extremely high intensities/fluencies and very short durations of multi-PW laser-driven ion beams demonstrated in our paper promise unique applications of these beams in various scientific domains, in order to make these applications reality, other parameters of the beams should be improved and the beam characteristics must be controlled and matched to the type of application envisaged.

For the application of ultra-intense laser-driven ion beams in nuclear physics, the ion energy spectrum width should be decreased and the ion energies should be controlled and adjusted to the requirements of a particular experiment. A significant narrowing of the ion energy spectrum (down to just a few percent) would create a chance to use light ion beams such as the carbon beam for medical applications, in particular for hadron cancer therapy. Both for applications in nuclear physics and medicine, it is desirable that the ion beams are generated with a high repetition rate (several Hz or higher) which is a significant challenge for multi-PW laser technology. Moreover, since in the above applications, especially in hadron therapy, the ion beam must usually be transported over a relatively long distance, the angular beam divergence should be as small as possible. Applications of ultra-intense ion beams in HED physics or ICF research do not require very high ion energies or very narrow ion energy spectra, and ion energies from several MeV/nucleon to tens of MeV/nucleon and spectral widths of 10–20% of the mean ion energy are usually sufficient for these applications. In addition, a high repetition rate of a laser driver is not necessary in order to perform HEDP or ICF experiments. However, for “full-scale” FI ICF experiments, the required values of ion beam power and energy are extremely high, attainable only with 100 kJ-class laser drivers, which will probably not be available in the near future. Fortunately, as was mentioned previously, fundamental research in ICF with multi-PW laser-driven ion beams will be possible with currently built multi-PW lasers.

The majority of applications of laser-driven ion beams require compact and cost-effective laser accelerators. The size, cost, and complexity of the accelerator are determined first of all by the laser driver, in particular by energy of the laser pulse produced by the driver. The way to minimize this energy without a significant reduction in the ion beam parameters is to increase the laser-to-ions energy conversion efficiency. One of the main challenges in the study of laser-driven ion acceleration is to increase this efficiency to a level ensuring compactness and cost of the accelerator enabling its practical usefulness.

The usefulness of laser-driven ion beams in scientific research as well as in technology or medicine also depends on whether at least some parameters of these beams can be higher/better than or comparable to those achieved in RF-driven accelerators. It is very likely that, in the foreseeable future, energies of laser-accelerated ions will still be considerably lower than the highest energies of ions achieved in large RF-driven accelerators. Obtaining in laser accelerators very narrow ion energy spectra whose spectral widths are comparable to those achieved in conventional accelerators is also rather unlikely. On the other hand, as was demonstrated in this paper, achieving peak ion beam intensities, peak ion current densities or ion fluencies higher than attainable presently in the RF-driven accelerators is feasible with currently built multi-PW lasers, so it is conceivable that it will be experimentally demonstrated over the next few years.