Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-11T12:18:13.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Time-dependent neutral-plasma isothermal expansions into a vacuum

Published online by Cambridge University Press:  12 December 2008

Y. Huang ,
X. Duan ,
X. Lan ,
Z. Tan ,
N. Wang ,
X. Tang  and
Y. He
Y. Huang*
Affiliation:
Department of Engineering Physics, Tsinghua University, Beijing, China and China Institute of Atomic Energy, Beijing, China
X. Duan
Affiliation:
China Institute of Atomic Energy, Beijing, China
X. Lan
Affiliation:
China Institute of Atomic Energy, Beijing, China
Z. Tan
Affiliation:
China Institute of Atomic Energy, Beijing, China
N. Wang
Affiliation:
China Institute of Atomic Energy, Beijing, China
X. Tang
Affiliation:
China Institute of Atomic Energy, Beijing, China
Y. He
Affiliation:
Department of Engineering Physics, Tsinghua University, Beijing, China
*
Address correspondence and reprint requests to: Yongsheng Huang, Department of Engineering Physics, Tsinghua University, Beijing 100084, China. E-mail: hyc05@mails.tsinghua.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

A time-dependent solution for neutral-plasma isothermal expansions into a vacuum in a special-transformation coordinate system is obtained. In this new coordinate system, the special self-similar solutions of it were given by Huang and co-workers (Appl. Phys. Lett. 92, 031501). Combining the time-dependent solution and the quasi-linear increase of the electron density due to the hot-electron recirculation, an analytic model is proposed to reveal the influence of the hot-electron recirculation on the increase of electric field and on the acceleration of ions of different masses and charges.

Keywords

Hot-electron recirculationLaser-ion accelerationTime-dependent
Type
Research Article
Information
Laser and Particle Beams , Volume 26 , Issue 4 , December 2008 , pp. 671 - 675
Copyright
Copyright © Cambridge University Press 2008

INTRODUCTION

The generation of energetic particles and acceleration mechanisms in the ultra-intense laser pulses interaction with plasmas have become an international research focus nowadays (Chen et al., Reference Chen, Unick, Vafaei-Najafabadi, Tsui, Fedosejevs, Naseri, Masson-Laborde and Rozmus2008; Karmakar & Pukhov, Reference Karmakar and Pukhov2007; Schwoerer et al., Reference Schwoerer, Pfotenhauer, Jackel, Amthor, Liesfeld, Ziegler, Sauerbrey, Ledingham and Esirkepov2006; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Kaluza et al., Reference Kaluza, Schreiber, Santala, Tsakiris, Eidmann, Meyer-ter-Vehn and Witte2004; d'Humires et al., Reference d'Humires, Lefebvre, Gremillet and Malka2005; Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001; Huang et al., Reference Huang, Lan, Duan, Tan, Wang, Shi, Tang and Xi2007, Reference Huang, Bi, Duan, Lan, Wang, Tang and He2008a, Reference Huang, Bi, Duan, Lan, Wang, Tang and He2008b). Some new schemes with novel targets (Limpouch et al., Reference Limpouch, Psikal, Andreev, Platonov and Kawata2008; Schwoerer et al., Reference Schwoerer, Pfotenhauer, Jackel, Amthor, Liesfeld, Ziegler, Sauerbrey, Ledingham and Esirkepov2006; Strangio et al., Reference Strangio, Caruso, Neely, Andreoli, Anzalone, Clarke, Cristofari, Del Prete, Di Giorgio, Murphy, Ricci, Stevens and Tolley2007; Schollmeier et al., Reference Schollmeier, Roth, Blazevic, Brambrink, Cobble, Fernandez, Flippo, Gautier, Habs, Harres, Hegelich, Hesslinga, Hoffmann, Letzring, Nurnberg, Schaumann, Schreiber and Witte2007) to enhance the ion acceleration and improve the quality of ion beams have been proposed. The progress of them can provide fundamental theory for inertial confined fusion (ICF) (Eliezer et al., Reference Eliezer, Murakaml and Val2007) and promote the realization of it effectively. The target normal sheath acceleration (TNSA) (Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001) is a generally accepted mechanism for the ion acceleration. However, the fundamental theory of TNSA is a special self-similar solution for neutral-plasma isothermal expansions into a vacuum (Mora, Reference Mora2003; Huang et al., 2008a, 2008b), which is time-independent in the transformation system. Whatever, the influence of the hot-electron recirculation has not been accounted for in the self-similar solution. Therefore, it is suitable for the target thickness larger than a critical value, L c. Mackinnon et al. (Reference Mackinnon, Sentoku, Patel, Price, Hatchett, Key, Andersen, Snavely and Freeman2002) observed enhancement of proton acceleration by hot-electron recirculation in thin foils whose thickness is less than L c. In addition, Sentoku et al. (Reference Sentoku, Cowan, Kemp and Ruhl2003) predicted an equation to conclude the influence of electron recirculation. However, they did not propose a clear description of electron recirculation. Their physical picture is too simple and not clear because n times of electron recirculations cannot happen all at once and the electron density cannot jump to n times of the initial density. Although Huang et al. (Reference Huang, Lan, Duan, Tan, Wang, Shi, Tang and Xi2007) have proposed the step model to describe the hot-electron recirculation in which the electron density increased step by step, the step model combined the Mora's result and the linear increase of the electron density easily. However, an analytic solution on the bases of the fundamental equations: the equations of continuity and motion of the ions are still needed to reveal the influence of the hot-electron recirculation on maximum ion velocity rationally.

In this paper, a time-dependent solution for neutral-plasma isothermal expansions into a vacuum and a simple model based on the equations of continuity, and motion of the ions are proposed to obtain the time-dependent electron density and maximum ion velocity for the target of arbitrary thickness. The model describes the hot-electron recirculation and the influence of it on the ion acceleration in the laser-foil interactions analytically. The maximum ion velocity given by our model for some target thicknesses have been compared with experiments (Mackinnon et al., Reference Mackinnon, Sentoku, Patel, Price, Hatchett, Key, Andersen, Snavely and Freeman2002; Kaluza et al., Reference Kaluza, Schreiber, Santala, Tsakiris, Eidmann, Meyer-ter-Vehn and Witte2004). Since the decrease of the laser absorption efficiency and the three-dimensional (3D) effect on the electron density have been ignored, the results given by our model are larger than the experimental data for thin targets. In order to understand the differences in some degree, the influence of the decrease of the laser absorption efficiency and the 3D effect on the ion acceleration have been discussed.

TIME-DEPENDENT TARGET NORMAL SHEATH ACCELERATION

For convenience, the physical parameters are normalized as follows:

(1)
\matrix{{\hat t = \omega _{\,pi0} t\comma \quad \hat l=l/\lambda _{D0}\comma \; } \cr{u=v/c_s\comma \quad \hat E=E/E_0\comma \quad \hat \phi=e\phi /k_B T_e }\comma \; \cr{\hat n=n/n_{e0}\comma \quad \hat c=c/c_s\comma \; } \cr}\eqno\lpar 1\rpar

where E is the electric field, n (n i or n e) is the density (ion or electron), n e0 is the reference hot-electron density at the rear of the target, φ is the electric potential, $c_s=\sqrt {Zk_B T_e /m_i }$ is the ion acoustic speed, $\omega _{\,pi0}=\sqrt {Zn_{e0} e^2 /m_i \epsilon _0 }$ is the initial ion plasma frequency, $\lambda _{D0}=c_s \omega_{pi0}$, c is the light speed and $E_0=k_B T_e /e\lambda _{D0} $. Here e is the elemental charge.

When a relativistic laser pulse interacts with a solid target, the laser-produced fast electrons with a unique temperature, $k_B T_e $, determined by the laser ponderomotive potential are instantly created in front of the target and propagate through the target collisionlessly, and then form a high energy plasma at the rear of the target. The hot-electrons at the rear of the target can be considered to be reflected by sheath field at the ion front (Santos et al., Reference Santos, Amiranoff, Baton, Gremillet, Koenig, Martinolli, Rabec Le Gloahec, Rousseaux, Batani, Bernardinello, Greison and Hall2002; Mora, Reference Mora2003) and come back to the front of the target, because the field there is strongest. No matter, the laser pulse exists or has gone, the hot electrons are assumed to be reflected back and forth between the front of the target and the ion front at the rear of the target. Furthermore, the electron beam is assumed to be in equilibrium with a single temperature k BT e. Let the zero time be when the hot electrons come to the rear of the target for the first time and t 0 = 0. For convenience, the hot-electron speed used is the light speed c. Therefore, the time is −L/c when the laser get to the front target, where L is solid target thickness. The electrons return back from the rear at t = 0 and arrive at the front of the target when t = L/c. For t ≤ t l, assuming the laser intensity is constant, the hot-electron temperature, $k_B T_e=m_e c^2 \lpar \gamma - 1\rpar $, is invariant due to the energy supply from the laser pulse. The plasma expansion is an isothermal expansion. Let $\mathop {\hat t}\nolimits_1 $ be the time when the hot electrons undergo a circle and reach the ion front again at the first time.

The reference frame used here is $\tau=\hat t\comma \; \xi=\hat x/\hat t$. With the transformation, the equations of continuity and motion are obtained easily in the new coordinate system.

The fast-electron density is a function of the parameters: the acceleration time, τ, the target thickness, L, laser intensity, I, laser focus radius, r L, the laser absorption efficiency, η, the incidence angle of the laser pulse, θin, the half-opening angle of fast electrons, θe and amplified spontaneous emission (ASE) duration, $\tau _{ASE} $. The laser absorption mechanisms in the femtosecond laser-plasma interactions determine the generation rate of the hot electrons, f, and then the laser absorption efficiency, η (Cai et al., Reference Cai, Yu, Zhu, Zheng, Cao and Pei2006). Assuming the time-dependent electron density for thin foils is variable-separating, then:

(2)
\matrix{{n_e \lpar \tau\comma \; \xi \rpar =N\lpar \tau \rpar N_e \lpar \xi \rpar \comma \; N\lpar \tau=\tau _L \rpar =1\comma \; } \cr}\eqno\lpar 2\rpar

where $\tau _L=2\hat L/c/\sqrt {2e}\comma \; N_e=n_{e0} \exp\!\lpar - \xi /\beta _1 - 1\rpar \comma \; n_{e0} $ is the hot-electron density when $t=t_L=2L/c\comma \; \beta _1 $ is a constant and N(τ) describes the increase of the maximum electron density due to electron recirculation and the electron generation by the laser-plasma interactions at the front of the target. The physical implication of β1 is the same as that given by Huang et al. (2008) and corresponds to $P_k=\lpar Z_k /M_k \rpar \lpar M/Z\rpar $ (where Z and M are the charge number and mass of the reference ion, Z k and M k are the charge number and mass of the concerned ion, respectively) in (Gurevich et al., Reference Gurevich, Anderson and Wilhelmsson1979). For different ions, β1 will be different. Therefore, the acceleration of ions of different masses and charges can be described with our model. If we choose the proton as the reference ion, β1 ≤ 1 for any other ions. Here, $N_e=n_{e0} \exp\!\lpar - \!\xi / \beta _1 - 1\rpar $ corresponds to the special self-similar solution given by Huang et al. (2008a, 2008b) and Gurevich et al. (Reference Gurevich, Anderson and Wilhelmsson1979) for the impurity ions. β1 = 1 corresponds to the classic self-similar solution given by Mora (Reference Mora2003).

Assuming that f is constant in the interval, t l, the hot-electron total number that propagate through the target when $t=t_l\comma \; N_t=\eta \lpar L\rpar E_l / \lpar k_B T_e \rpar $ for t l≤t L, and $N_t=\eta \lpar L\rpar E_l t_L /\lpar k_B T_e t_l \rpar $ for t l ≥ t L, where E l is the laser energy. Using Eq. (2) (Kaluza et al., Reference Kaluza, Schreiber, Santala, Tsakiris, Eidmann, Meyer-ter-Vehn and Witte2004), with N t, then n e0 in Eq. (2) can be estimated by:

(3)
n_{e0}={{4.077\eta \lpar L\rpar I_{10^{18} {\rm W/cm^2} } } \over {\lpar \gamma - 1\rpar \lpar 1+\lpar L^{\ast} /r_L \rpar {\rm tan}\lpar \theta _{\rm e} \rpar \rpar ^2 }}\comma \; t_L \leq t_l\comma \; \eqno\lpar 3\rpar

where r L is the laser pulse focus radius, $L^{\ast} = L / \cos\lpar \theta _{in}\rpar $ is the efficient target thickness, θin is the incidence angle of the laser pulse, and θe ≈ 17° is half-opening angle of the superathermal electrons which was measured by Santos et al. (Reference Santos, Amiranoff, Baton, Gremillet, Koenig, Martinolli, Rabec Le Gloahec, Rousseaux, Batani, Bernardinello, Greison and Hall2002). When r L≫L and $\tan\lpar \theta _{in} \rpar \ll 1\comma \; \lpar 1+\lpar L^{\ast} /r_L \rpar \tan\lpar \theta _{in} \rpar \rpar ^2 \approx 1$, the angular effect can be neglected. Therefore, the influence of $\eta \lpar \hat L\rpar $ and electron recirculation become dominated for thin targets.

As usual, assuming that the hot electrons satisfy uniform distribution in the bulk from the front of the target to the ion front and $f=\bar f$ where $\bar f$ is the mean value of f, N(τ) can be roughly described by:

(4)
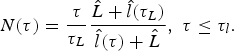
N\lpar \tau \rpar ={\tau \over {\tau _L }}{{\hat L+\hat l\lpar \tau _L \rpar } \over {\hat l\lpar \tau \rpar +\hat L}}\comma \; \tau \leq \tau _l. \eqno\lpar 4\rpar

For τL ≤ τl, the electron density increases continuously until t = t l. With Eq. (4), the maximum value of N(τ) is larger than 1, which can describe hot-electron recirculation (Mackinnon et al., Reference Mackinnon, Sentoku, Patel, Price, Hatchett, Key, Andersen, Snavely and Freeman2002; Sentoku et al., Reference Sentoku, Cowan, Kemp and Ruhl2003; Huang et al., Reference Huang, Lan, Duan, Tan, Wang, Shi, Tang and Xi2007). However, for τL ≥ τl, the maximum value of N(τ) is smaller than 1. Therefore, it is assumed conveniently that the hot-electron recirculation stop synchronously with laser pulse ending. As pointed by Huang et al. (2007), the critical condition for hot-electron recirculation is τL = τl and the critical target thickness is: L c = 0.5ct l. Therefore, hot-electron recirculation should be considered for L ≤ L c.

With the quasi-neutral approximation, $n_i=n_e=Nn_{e0} $$\exp\!\lpar\! - \!\xi /\beta _1 - 1\rpar $. Solving the equations of continuity and motion of ions, the time-dependent ion velocity and potential are $u_i=\xi+\beta _1+\beta _1 \delta \lpar \tau \rpar \comma \; \hat \phi=- \beta _1 \xi - \beta _1^2+\phi _1 \lpar \tau\comma \; \xi \rpar $, where $\delta \lpar \tau \rpar =\tau \partial \,\hbox{ln}\,N\lpar \tau \rpar /\partial \tau $, and $\phi _1=- \beta _1 \lpar 2\tau \partial \,\hbox{ln}\,N/\partial \tau+\tau ^2 \partial ^2 \,\hbox{ln}\,N/\partial \tau ^2 \rpar \xi $. With this, neutral condition of the plasma is still satisfied. Therefore, the zero-ion-velocity position should be: $\xi _{u_i=0}=- \beta _1 \lsqb 1+\tau \partial \,\hbox{ln}\,N\lpar \tau \rpar /\partial \tau \rsqb $ or $x_{u_i=0}=- \tau \beta _1 \lsqb 1+\tau \partial \,\hbox{ln}\,N\lpar \tau \rpar /\partial \tau \rsqb $. For N ≡ 1, the result is the same as the self-similar solution's result (Huang et al., 2008a, 2008b). Therefore the dependence of the ion velocity on the time is:

(5)
u_i=\hbox{ln}\lpar \tau ^{\beta _1 } N\rpar +\beta _1 \tau \partial \,\ln\,N\lpar \tau \rpar /\partial \tau. \eqno\lpar 5\rpar

Eq. (5) shows the influence of the time-dependent electron density on the ion acceleration. Now the first part of Eq. (5) is ln(τN) compared with ln(τ) in the classic solution (Mora, Reference Mora2003). For N > 1, the hot-electron recirculation affects the ion acceleration. The second part exists for $\partial \,\hbox{ln}\,N\lpar \tau \rpar /\partial \tau \ne 0$ that means time-dependent. For N ≡ 1, Eq. (5) returns to the self-similar solution (Huang et al., 2008a, 2008b), which is time-independent.

The ion velocity at the ion front is the maximum ion velocity. Beyond the ion front, the ion density is zero and the electron density is still demonstrated by Eq. (2). The field for the ions at $\xi\lt \xi _{i\comma f} $, where $\xi _{i\comma f} $ is the self-similar variable at the ion front, is shielded by the ions beyond them. Therefore, the ion velocity at the ion front is larger than the ion velocity at $\xi\lt \xi _{i\comma f} $ and can not be described by Eq. (5), and should be obtained by another way. There are two methods to obtain the ion-front velocity: a mathematical way used by Huang et al. (2008a, 2008b); a physical way given by Mora (Reference Mora2003). For convenience, the physical way will be used here. Similar with Mora's discussion (Mora, Reference Mora2003), using $\lambda _D=\lambda _{D0} \lpar n_{e0} /n_e \rpar ^{1/2}=c_s t$, the ion velocity at the ion front is given by:

(6)
u_{i\comma f}=\beta _1 \hbox{ln}\lpar \tau ^2 N\rpar +\beta _1 \tau \partial\, \ln N\lpar \tau \rpar /\partial \tau.\eqno\lpar 6\rpar

Eq. (6) shows that the ion velocity at the ion front is larger than that given by Eq. (5) and $u_{i\comma f} - u_i=\beta _1 \ln\lpar \tau \rpar $.

Eqs. (4) and (6) are combined to give: $u_{i\comma f}=C_1 \lpar t\rpar$$ \beta _1 \lsqb \hbox{ln}\lpar \tau ^2\, N\rpar +1\rsqb $, where $C_1 \lpar t\rpar =\lpar \hat l\lpar \tau \rpar +\hat L\rpar /\lpar \hat l\lpar \tau \rpar +\hat L+\beta _1 \tau \rpar $. For $\hat l\lpar \tau \rpar + \hat L \gg \tau $ at $\tau \leq \tau _{acc} $, $C_1 \approx 1.\, \hat l\lpar \tau \rpar $ is the position of the ion front. With $u_{i\comma f}=0$, the beginning time of the ion acceleration is: $\tau _b=\lsqb \lpar \tau _L /e\rpar \hat L/\lpar \hat L+\hat l\lpar \tau _L \rpar \rpar \rsqb ^{1/3} $, here $e=2.71828...$. Therefore, the position of the ion front is decided by:

(7)
\eqalign{dF/d\tau &= \lpar \beta _1 F/\lpar F+\beta _1 \tau \rpar \rpar \lsqb \hbox{ln}\lpar \tau ^3 F_L /\tau _L F\rpar +1\rsqb \comma \; \tau \in \lsqb \tau _b\comma \; \tau _{acc} \rsqb .}\eqno\lpar 7\rpar

where $F=\hat L+\hat l\lpar \tau \rpar $ and $F_L=\hat L+\hat l\lpar \tau _L \rpar $.

However, for $l_f \lpar \tau _L \rpar \approx l_f \lpar \tau _{acc} \rpar $ or $L \gg l_f \lpar \tau _{acc}\rpar \comma \; N\lpar \tau _{acc}\comma \, L\rpar \approx $ (L c/L)(L+l f (τL)/(L+l f (τacc)))≈L c/L, $\tau \partial \,\hbox{ln}\,N\lpar \tau \rpar /\partial \tau \approx 1$ at $\tau=\tau _{acc} $, where τacc is the normalized acceleration time and a little longer than the laser pulse duration. Therefore, $u_{i\comma f} \approx \beta _1 \hbox{ln}\lsqb t_{acc}^2 \lpar L_c /L\rpar \lpar \eta /\eta _s \rpar \rsqb +$$C\comma \; L \leq L_c $, where ηs is the saturate laser absorption efficiency for large target thickness and about 30–50% C is a constant and $t_{acc} \approx \lpar 1 \sim 2\rpar t_l $ is the physical acceleration time. The self-similar ion velocity at the ion front given by Huang et al. (2008a, 2008b) is $\beta _1 \hbox{ln}\lpar t_{acc}^2 \lpar \eta /\eta _s \rpar \rpar +C$, which is suitable for the target thickness larger than L c since the hot-electron recirculation has not been accounted for. Sentoku et al.'s model (2003) shows that: $u_{i\comma f} \propto \sqrt {L_c /L}\, \ln\lpar t\rpar $. However, the key physical relation given by Huang et al.'s (2007) step model is about $2\sqrt {L_c /L}\, \ln\lpar t_{acc} \sqrt {\eta /\eta _s }\rpar $.

With above discussions, the dependence of laser absorption efficiency on the target thickness becomes the most important unknown information. With Eq. (3), for $L \leq r_L$ and $\lpar L^{\ast} / r_L \rpar \tan\lpar \theta _{\rm e} \rpar \ll 1$, the reference electron density $n_{e0} \approx 4.077 \eta \lpar L\rpar I_{10^{18} {\rm W/cm^2} } t_L /\lpar \gamma - 1\rpar t_l $ and is proportional to laser absorption efficiency and target thickness. When the laser absorption efficiency tends to zero with $L \to 0$, $n_{e0} \to 0$ and the maximum ion velocity tends to zero too. d'Humires et al. (Reference d'Humires, Lefebvre, Gremillet and Malka2005) have given a curve to describe that, but can it be used for any other target or other parameters of laser pulse? However, the changing law should be similar, the exact relationship have not been obtained. In fact, the dependence of opening angle of electrons on the target thickness and laser parameters is also important for the electron density, and the opening angle of ions to be ascertained, but still a challenge. The angle decides the electron density n e0 as shown in Eq. (3) and increases with target thickness. Therefore, for thin target, the opening angle should be smaller than 17° (Santos et al., Reference Santos, Amiranoff, Baton, Gremillet, Koenig, Martinolli, Rabec Le Gloahec, Rousseaux, Batani, Bernardinello, Greison and Hall2002) and becomes zero when $L \to 0$.

COMPARISON WITH EXPERIMENTS AND DISCUSSION

In fact, to compare our model with the relative experiments exactly, $\eta=\eta \lpar L\comma \; I\comma \; \lambda\comma \; r_L\rpar $ and $\theta _e=\theta _e \lpar L\comma \; I\comma \; \lambda\comma \; r_L\rpar $ should be ascertained first. However, Figure 1 shows a course comparison with the assumptions: laser absorption efficiency and the opening angle of electrons are fixed for different target thicknesses, η = 40%, θe = 17°, and β1 = 1. Other parameters are the same as the compared experiments. With Figure 1a, the results of our model are consistent with the experimental data. In these experiments, Mackinnon et al. (Reference Mackinnon, Sentoku, Patel, Price, Hatchett, Key, Andersen, Snavely and Freeman2002), the contrast ratio of intensity is large enough that the influence of the prepulse can be neglected. Therefore, for L ≳ 1 µm, the laser absorption efficiency sustains a constant. However, if the contrast ratio is not large enough and the influence of the prepulse on η can not be ignored, η should not be assumed to be a constant and the results given by our model are larger than experimental data as shown by Figure 1b. It is concluded that for L ≤ L c, the influence of the hot-electron recirculation on the ion acceleration is evident: maximum ion energy increases quickly with the decrease of the target thickness and larger than the experimental data.

Fig. 1. (Color online) Comparisons with Kaluza et al.'s and Mackinnon et al.'s experiments, where the unit of I is 1018 W/cm2. Kaluza et al.'s experimental parameters are: λ = 790 nm, r L = 2.5 µm, t l = 150 fs and t ASE = 2.5 ns, I = 1.0 × 1019 W/cm2, I = 1.3 × 1019 W/cm2 and I = 1.5 × 1019 W/cm2 with incidence of 30° onto targets, and laser absorption efficiency is about 40%; Mackinnon et al.'s experimental parameters are: λ = 0.8 µm, r L = 2.5 µm, t l = 100 fs, intensity contrast ratio is 1010: 1 with incidence of 22° onto targets, and laser absorption efficiency is 40%. In our model, the half opening angle of electrons is 17°(Santos et al., Reference Santos, Amiranoff, Baton, Gremillet, Koenig, Martinolli, Rabec Le Gloahec, Rousseaux, Batani, Bernardinello, Greison and Hall2002).

The reasons for larger results given by our model may be:

(1) the parameters of laser absorption efficiency is taken as constants. In fact, the laser absorption efficiency stays constant for the target of thickness large enough and decreases with the decrease of the target thickness for thin foils and tends to zero as $L \to 0$ shown by Fig. 12 in (d'Humires et al., Reference d'Humires, Lefebvre, Gremillet and Malka2005) with particle-in-cell simulations. In general cases, the analytic function of the dependence of laser absorption efficiency on target thickness, laser intensity, laser pulse duration and ASE duration is still a challenge, although Huang et al. has a half-analytic way to obtain it (Huang et al., Reference Huang, Lan, Duan, Tan, Wang, Shi, Tang and Xi2007). Here, the function can also be concluded with the similar method. It is easy to realized and is not repeated here.

(2) the three dimensional effect is not contained. The electron density does decrease with the plasma expansion as the electrons recirculate and spread laterally with a given opening angle. This dilute effect of the electron density is ignored here. In our sequence articles, it will be considered.

CONCLUSION

In conclusion, the time-dependent isothermal expansion for the target normal sheath proton acceleration is briefly proposed. The influence of hot-electron recirculation on the ion acceleration has been shown by Eq. (6) analytically and by Figure 1 obviously. For L ≤ L c, the hot-electron recirculation enhances the ability of the ion acceleration for thin foils.

ACKNOWLEDGMENTS

This work was supported by the Key Project of Chinese National Programs for Fundamental Research (973 Program) under contract No. 2006CB806004 and the Chinese National Natural Science Foundation under contract No. 10334110.

References

REFERENCES

Cai, H.B., Yu, W., Zhu, S.P., Zheng, C.Y., Cao, L.H. & Pei, W.B. (2006). Vacuum heating in the interaction of ultrashort relativistically strong laser pulses with solid targets. Phys. Plasmas 13, 063108–6.CrossRefGoogle Scholar
Chen, Z.L., Unick, C., Vafaei-Najafabadi, N., Tsui, Y.Y., Fedosejevs, R., Naseri, N., Masson-Laborde, P.E. & Rozmus, W. (2008). Quasi-monoenergetic electron beams generated from 7 TW laser pulses in N-2 and He gas targets. Laser Part. Beams 26, 147–155.CrossRefGoogle Scholar
d'Humires, E., Lefebvre, E., Gremillet, L. & Malka, V. (2005). Proton acceleration mechanisms in high-intensity laser interaction with thin foils. Phys. Plasmas 12, 062704–13.CrossRefGoogle Scholar
Eliezer, S., Murakaml, M. & Val, J.M.M. (2007). Equation of state and optimum compression in inertial fusion energy. Laser Part. Beams 25, 585–592.CrossRefGoogle Scholar
Flippo, K., Hegelich, B.M., Albright, B.J., Yin, L., Gautier, D.C., Letzring, S., Schollmeier, M., Schreiber, J., Schulze, R. & Fernandez, J.C. (2007). Laser-driven ion accelerators: Spectral control, monoenergetic ions and new acceleration mechanisms. Laser Part. Beams 25, 3–8.CrossRefGoogle Scholar
Gurevich, A., Anderson, D. & Wilhelmsson, H. (1979). Ion acceleration in an expanding plasma with non-Maxwellian electrons. Phys. Rev. Lett. 42, 769–764.CrossRefGoogle Scholar
Huang, Y.S., Bi, Y.J., Duan, X.J., Lan, X.F., Wang, N.Y., Tang, X.Z. & He, Y.X. (2008). Self-similar neutral-plasma isothermal expansion into a vacuum. Appl. Phys. Lett. 92, 031501–3.CrossRefGoogle Scholar
Huang, Y.S., Bi, Y.J., Duan, X.J., Lan, X.F., Wang, N.Y., Tang, X.Z. & He, Y.X. (2008). Energetic ion acceleration with a non-Maxwellian hot-electron tail. Appl. Phys. Lett. 92, 141504–3.CrossRefGoogle Scholar
Huang, Y.S., Lan, X.F., Duan, X.J., Tan, Z.X., Wang, N.Y., Shi, Y.J., Tang, X.Z. & Xi, H.Y. (2007). Hot-electron recirculation in ultraintense laser pulse interactions with thin foils. Phys. Plasmas 14, 103106–6.CrossRefGoogle Scholar
Kaluza, M., Schreiber, J., Santala, M.I.K., Tsakiris, G.D., Eidmann, K., Meyer-ter-Vehn, J. & Witte, K.J. (2004). Influence of the laser prepulse on proton acceleration in thin-foil experiments. Phys. Rev. Lett. 93, 045003–4.CrossRefGoogle ScholarPubMed
Karmakar, A. & Pukhov, A. (2007). Collimated attosecond GeV electron bunches from ionization of high-Z material by radially polarized ultra-relativistic laser pulses. Laser Part. Beams 25, 371–377.CrossRefGoogle Scholar
Limpouch, J., Psikal, J., Andreev, A.A., Platonov, K.Y. & Kawata, S. (2008). Enhanced laser ion acceleration from mass-limited targets. Laser Part. Beams 26, 225–234.CrossRefGoogle Scholar
Mackinnon, A.J., Sentoku, Y., Patel, P.K., Price, D.W., Hatchett, S., Key, M.H., Andersen, C., Snavely, R. & Freeman, R.R. (2002). Enhancement of proton acceleration by hot-electron recirculation in thin foils irradiated by ultraintense laser pulses. Phys. Rev. Lett. 88, 215006–4.CrossRefGoogle ScholarPubMed
Mora, P. (2003). Plasma expansion into a vacuum. Phys. Rev. Lett. 90, 185002–4.CrossRefGoogle ScholarPubMed
Murakami, M. & Basko, M.M. (2006). Self-similar expansion of finite-size non-quasi-neutral plasmas into vacuum: Relation to the problem of ion acceleration. Phys. Plasmas 13, 012105–7.CrossRefGoogle Scholar
Santos, J.J., Amiranoff, F., Baton, S.D., Gremillet, L., Koenig, M., Martinolli, E., Rabec Le Gloahec, M., Rousseaux, C., Batani, D., Bernardinello, A., Greison, G. & Hall, T. (2002). Fast electron transport in ultraintense laser pulse interaction with solid targets by rear-side self-radiation diagnostics. Phys. Rev. Lett. 89, 025001–4.CrossRefGoogle ScholarPubMed
Schollmeier, M., Roth, M., Blazevic, A., Brambrink, E., Cobble, J.A., Fernandez, J.C., Flippo, K.A., Gautier, D.C., Habs, D., Harres, K., Hegelich, B.M., Hesslinga, T., Hoffmann, D.H.H., Letzring, S., Nurnberg, F., Schaumann, G., Schreiber, J. & Witte, K. (2007). Laser ion acceleration with micro-grooved targets. Nucl. Instr. Meth. Phys. Res. A 577, 186–190.CrossRefGoogle Scholar
Schwoerer, H., Pfotenhauer, S., Jackel, O., Amthor, K.-U., Liesfeld, B., Ziegler, W., Sauerbrey, R., Ledingham, K.W.D. & Esirkepov, T. (2006). Laser-plasma acceleration of quasi-monoenergetic protons from microstructured targets. Nature 439, 445–8;CrossRefGoogle ScholarPubMed
Sentoku, Y., Cowan, T.E., Kemp, A. & Ruhl, H. (2003). High energy proton acceleration in interaction of short laser pulse with dense plasma target. Phys. Plasmas 10, 2009–2015.CrossRefGoogle Scholar
Strangio, C., Caruso, A., Neely, D., Andreoli, P.L., Anzalone, R., Clarke, R., Cristofari, G., Del Prete, E., Di Giorgio, G., Murphy, C., Ricci, C., Stevens, R. & Tolley, M. (2007). Production of multi-MeV per nucleon ions in the controlled amount of matter mode (CAM) by using causally isolated targets. Laser Part. Beams 25, 85–91.CrossRefGoogle Scholar
Wilks, S.C., Kruer, W.L., Tabak, M. & Langdon, A.B. (1992). Absorption of ultra-intense laser pulses. Phys. Rev. Lett. 69, 1383–1384.CrossRefGoogle ScholarPubMed
Wilks, S.C., Langdon, A.B., Cowan, T.E., Roth, M., Singh, M., Hatchett, S., Key, M.H., Pennington, D., MacKinnon, A. & Snavely, R.A. (2001). Energetic proton generation in ultra-intense laser-solid interactions. Phys. Plasmas 8, 542–548.CrossRefGoogle Scholar
Figure 0

Fig. 1. (Color online) Comparisons with Kaluza et al.'s and Mackinnon et al.'s experiments, where the unit of I is 1018 W/cm2. Kaluza et al.'s experimental parameters are: λ = 790 nm, rL = 2.5 µm, tl = 150 fs and tASE = 2.5 ns, I = 1.0 × 1019 W/cm2, I = 1.3 × 1019 W/cm2 and I = 1.5 × 1019 W/cm2 with incidence of 30° onto targets, and laser absorption efficiency is about 40%; Mackinnon et al.'s experimental parameters are: λ = 0.8 µm, rL = 2.5 µm, tl = 100 fs, intensity contrast ratio is 1010: 1 with incidence of 22° onto targets, and laser absorption efficiency is 40%. In our model, the half opening angle of electrons is 17°(Santos et al., 2002).