1. INTRODUCTION
Shockwaves constitute one of the most basic concepts in fluid mechanic. Already in 1808, Poisson derived the non-linear equation for the evolution of a large amplitude sound wave (Poisson, Reference Poisson1808). Few years later, in 1848, Stokes understood that the solutions of the equation derived by Poisson necessarily evolve a discontinuity, that is, what we now call a “shockwave” (Stokes, Reference Stokes1848; Salas, Reference Salas2007).
Shockwaves can also be generated when two media move with respect to each other at a velocity larger than the speed of sound in one of them. Owing to such a large amount of potential, and mundane, generators, shockwaves are ubiquitous in fluid mechanic. Of course, the shock front is not a mathematical discontinuity. In order to slow down at the front, an upstream particle can only collide more often with the others. The shock front is therefore a few mean-free path thick, that is, a discontinuity in the fluid limit. Here, the front size is of the order of the mean-free path (Zel'dovich & Raizer, Reference Zel'dovich and Raizer2002).
Let us now turn to the Earth bow shock, namely, the shock of the Earth magnetosphere within the solar wind. In situ measurements by the 4 “Cluster” satellites indicate a shock front some 100 km thick (Bale et al., Reference Bale, Mozer and Horbury2003; Schwartz et al., Reference Schwartz, Henley, Mitchell and Krasnoselskikh2011). Yet, the proton mean-free path at this location is about 108 km (Kasper et al., Reference Kasper, Lazarus and Gary2008). Here, the shock front is six orders of magnitude smaller than the mean-free path. How can this be?
Starting with the pioneering works of Sagdeev (Reference Sagdeev1966), such shocks have been studied from the 1960s and dubbed “collisionless shocks”. A number of review paper are now available, where the reader will find about our current knowledge regarding their characteristics, both macroscopic and microscopic (Treumann, Reference Treumann2009; Marcowith et al., Reference Marcowith, Bret, Bykov, Dieckman, Drury, Lembège, Lemoine, Morlino, Murphy, Pelletier, Plotnikov, Reville, Riquelme, Sironi and Stockem Novo2016). Among the various aspects of these shocks that are currently under investigation, the way they are formed is of significant importance, be it to guide experimental efforts aiming at producing them in the laboratory (Fiuza et al., Reference Fiuza, Fonseca, Tonge, Mori and Silva2012; Chen et al., Reference Chen, Nakai, Sentoku, Arikawa, Azechi, Fujioka, Keane, Kojima, Goldstein, Maddox, Miyanaga, Morita, Nagai, Nishimura, Ozaki, Park, Sakawa, Takabe, Williams and Zhang2013; Sarri et al., Reference Sarri, Poder, Cole, Schumaker, Di Piazza, Reville, Doria, Dromey, Gizzi, Green, Grittani, Kar, Keitel, Krushelnick, Kushel, Mangles, Najmudin, Thomas, Vargas and Zepf2015). Such is the topic of this paper.
Beside their ubiquity in astrophysics, collisionless shocks have been under scrutiny for decades (Bell, Reference Bell1978; Blandford & Ostriker, Reference Blandford and Ostriker1978), because they could hold the key to two of the most intriguing contemporary enigmas: high-energy cosmic-rays and gamma-ray bursts (Vietri et al., Reference Vietri, De Marco and Guetta2003; Piran, Reference Piran2005).
As previously noted, a fluid shock can be launched by colliding two media at a velocity larger than the speed of sound in one of them. However, if both media are collisionless plasmas shells, there is no “collision”, as the two shells will start interpenetrating instead. At low energy, the interaction between them can be mediated by the potential jump originating from the Debye sheets at their borders (if any) (Stockem et al., Reference Stockem, Fiuza, Bret, Fonseca and Silva2014). But at high energies, each shell seamlessly runs over the Debye sheet of the other, and the region where the two shells overlap features a counter-streaming plasma system. This counter-streaming system is the key to the shock formation.
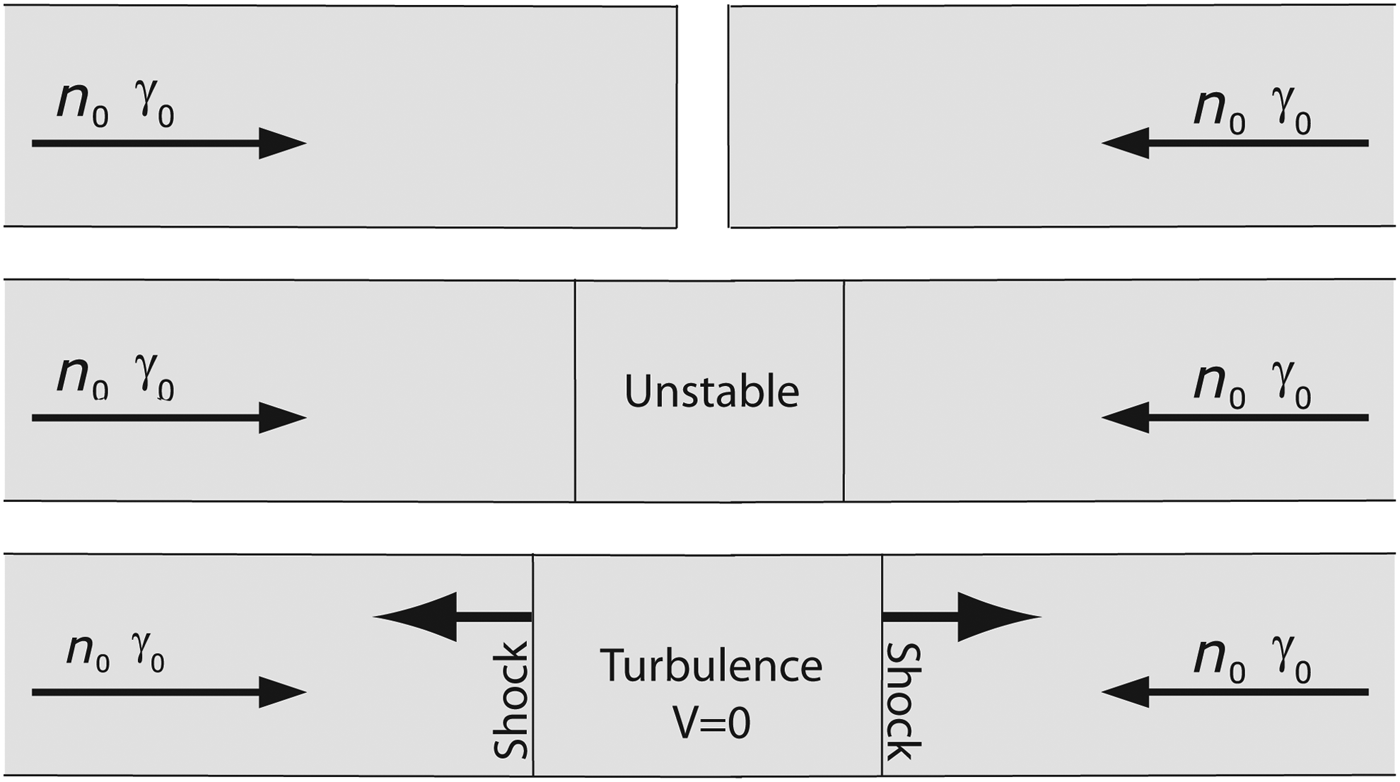
Counter-streaming plasma systems are notoriously unstable. Consider Figure 1, with symmetric, initially cold shells, heading toward each other with a Lorentz factor γ0. The dominant instability in the overlapping region is the Weibel one as soon as 
${{\rm \gamma} _0} \gt \sqrt {3/2} $ (Bret et al., Reference Bret, Stockem, Fiúza, Ruyer, Gremillet, Narayan and Silva2013). It grows unstable modes with a wave vector normal to the flow.
Fig. 1. Setup considered. Two plasma shells are heading toward each other. As they overlap, the overlapping region turns Weibel unstable. After the trapping time τp, the turbulence in the central region has become strong enough to trap the incoming flow. The shock formation follows. In Section 2, two pair plasma shells are considered. In Section 3, these are two electron/proton plasmas.
Although the unstable “history” differs whether one deals with pair or electron/proton plasmas, the outcome is the same in both cases: after a time τp that we shall call the “trapping time”, the flow which keeps entering the overlapping region is trapped inside. The growth of one, or various, instabilities generated enough turbulence to block the incoming flow. From the macroscopic point of view, we thus have a region of space, the overlapping region at t = τp, where the bulk velocity is 0. This is the onset of the shock formation.
As already hinted, the saturation time is not reached the same way whether the system consists in pair, or electron/proton plasmas. This is why the rest of the paper is divided into two main parts. In Section 2, the case of pair plasmas is examined. We also explain here how the system evolves from the trapping time to the shock formation time. Then in Section 3, we turn to the slightly more involved case of electron/proton plasmas. Finally, the validity of the Rankine–Hugoniot (RH) relations for a collisionless shock is discussed in Section 4.
2. PAIR PLASMAS
The encounter of two relativistic, symmetric, un-magnetized, and cold pair plasmas shells is the simplest possible setting in various respects. The absence of mass difference between species renders particle-in-cell (PIC) simulations easier. In the cold un-magnetized regime, we have exact analytical expressions for the growth rates of the instabilities involved (Bludman et al., Reference Bludman, Watson and Rosenbluth1960; Faĭnberg et al., Reference Faĭnberg, Shapiro and Shevchenko1970; Bret et al., Reference Bret, Gremillet and Dieckmann2010a). Finally, the dominant instability (Weibel) is always the same in the relativistic regime (Bret et al., Reference Bret, Firpo and Deutsch2005; Bret & Deutsch, Reference Bret and Deutsch2006; Bret et al., Reference Bret, Gremillet, Bénisti and Lefebvre2008).
The setup considered is pictured in Figure 1. In the present case of two pair plasmas, both electrons and positrons turn unstable when the shells start to overlap. All kinds of unstable modes grow out of the interaction, but the fastest growing ones are the Weibel modes. There are found for a wave vector normal to the flow, which is why they form filaments (Huntington et al., Reference Huntington, Fiúza, Ross, Zylstra, Drake, Froula, Gregori, Kugland, Kuranz, Levy, Li, Meinecke, Morita, Petrasso, Plechaty, Remington, Ryutov, Sakawa, Spitkovsky, Takabe and Park2015). In the relativistic regime, their growth rate is (Bret et al., Reference Bret, Gremillet and Dieckmann2010b),
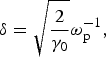$${\rm \delta} = \sqrt {\displaystyle{2 \over {{{\rm \gamma} _0}}}} {\rm \omega} _{\rm p}^{ - 1}, $$
where 
${\rm \omega} _{\rm p}^2 = 4{\rm \pi} {n_0}{e^2}/{m_{\rm e}}$ is the electronic, or positronic, plasma frequency of the shells.
We thus have the Weibel instability growing, until it saturates at the saturation time τs which can be determined in terms of the growth rate (1), the field at saturation, and the spontaneous fluctuations of the shells before they collide (Bret et al., Reference Bret, Stockem, Fiúza, Ruyer, Gremillet, Narayan and Silva2013). When Weibel reaches saturation, the density in the overlapping region is still the sum of the two shells’ density. The reason for this is that just before saturation, the linear regime was still valid, imposing only slight density perturbations. If, then, the density in the central region was still ~2n 0 at τs −ε, it cannot be otherwise at τs. At this stage, the density “jump” is therefore only 2, far from the one expected from the RH relation (see Section 4).
How then is a shock formed from this point? By trapping the incoming flow in the overlapping region. Indeed, this region of space is now occupied by magnetic filaments, which peak field value and characteristic length are known (Davidson et al., Reference Davidson, Hammer, Haber and Wagner1972). From these data, one can compute the distance L the incoming flow can cover before being randomized (Lyubarsky & Eichler, Reference Lyubarsky and Eichler2006; Bret, Reference Bret2015). As it turns, L is always smaller than the size of the overlapping region at saturation (Bret et al., Reference Bret, Stockem, Fiúza, Ruyer, Gremillet, Narayan and Silva2013, Reference Bret, Stockem, Narayan and Silva2014). As a consequence, this region no longer expands after saturation, and the bulk velocity inside is 0. Here, the trapping time is therefore identical to the saturation time, τp = τs.
A shock has just been formed in velocity space. From this moment, the density in the central region is going to increase until it meets the expected density jump, namely 3 in 2 dimensions, and 4 in 3 dimensions (Blandford & McKee, Reference Blandford and McKee1976; Stockem et al., Reference Stockem, Fiúza, Fonseca and Silva2012). If it took one saturation time τs to bring the central density from 1 to 2, and assuming the same region no longer expands after saturation, then we shall need to wait another saturation time to raise the density jump to 3 [in two-dimensional (2D)], and yet another saturation time to raise it to 4 (in 3D). The shock formation time is therefore given by,
$${{\rm \tau} _{\rm f}} = d {{\rm \tau} _{\rm p}},$$where d is the dimension of the problem. Note that this line of reasoning holds regardless of the shells’ composition. It only relies on the expected density jump, and on the flow being trapped at trapping time. Hence, Eq. (1) is also valid for the case we now turn to, namely, electron/proton plasmas shells.
3. ELECTRON/PROTON PLASMAS
This case can still be pictured by Figure 1, where each shell is now made of protons and electrons. Due to their smaller inertia, electrons turn Weibel unstable first, and grow magnetic filaments of size λe and peak field B e. Meanwhile, protons keep ploughing through the resulting bath of hot electrons, and in turn get unstable. Here also, a number of unstable modes grow, but investigations of the full unstable spectrum showed that the fastest growing modes are, again, the Weibel's ones (Shaisultanov et al., Reference Shaisultanov, Lyubarsky and Eichler2012).
As it is triggered, the protons’ Weibel instability does not start from a perfectly clean medium, but from a plasma where magnetic filaments of size λe can already be found. Simply put, an unstable mode is already seeded, and it is further grown by the protons’ Weibel instability. When it reaches saturation, the peak field in the filaments in now
$${B_{\rm i}} = \sqrt {\displaystyle{{{m_{\rm p}}} \over {{m_{\rm e}}}}} {B_{\rm e}},$$where m p is the proton mass. But their size is still the same, since the linear regime leaves unchanged the k it grows.
Can magnetic filaments of size λe and peak field B i efficiently trap the incoming ions? The answer is no. The main problem is that λe is of the order of the electronic Larmor radius in the field B e. In order to block the protons, λe should also be the Larmor radius of the protons in the field B i (Bret, Reference Bret2015). Considering Eq. (3), one finds λe is 
$\sqrt {{m_{\rm e}}/{m_{\rm p}}} $ too short for this. Therefore, at this stage, protons keep streaming through the overlapping region.
Fortunately, another process, widely studied in relation with the non-linear evolution of the Weibel instability, allows reaching the trapping time. It has been known for long that in this regime, the magnetic filaments originated by the growth of the instability, progressively merged, and increase in size. A model for this growth, backed up by 2D and 3D PIC simulations, found that the size of the filaments grows linearly with time (Medvedev et al., Reference Medvedev, Fiore, Fonseca, Silva and Mori2005). The same model allows us therefore to compute the time it takes for the filaments to reach the correct size. Summing up this merging time to the saturation time of the protons’ Weibel instability (that of the electrons can be neglected), we find for the trapping time (Stockem Novo et al., Reference Stockem Novo, Bret, Fonseca and Silva2015),
$${{\rm \tau} _{\rm p}} = 4.43 \sqrt {{{\rm \lambda} _0}} \ln \displaystyle{{{m_{\rm p}}} \over {{m_{\rm e}}}}{\rm \omega} _{{\rm pp}}^{ - 1}, $$
where 
${\rm \omega} _{{\rm pp}}^2 = 4\pi {n_0}{e^2}/{m_{\rm p}}$ is the protonic plasma frequency of the shells. Following the reasoning explained at the end of the previous section, the shock formation time is now,
$${{\rm \tau} _{\rm f}} = 4.43 d \sqrt {{{\rm \lambda} _0}} \ln \displaystyle{{{m_{\rm p}}} \over {{m_{\rm e}}}}{\rm \omega} _{{\rm pp}}^{ - 1}. $$Note that if m p = m e, this equation does not reduce to the shock formation time for pair plasmas since the electronic Weibel phase has been neglected. A series of 2D PIC simulations has been performed with the code OSIRIS to test our result (Fonseca et al., Reference Fonseca, Silva, Tsung, Decyk, Lu, Ren, Mori, Deng, Lee, Katsouleas, Adam, Sloot, Hoekstra, Tan and Dongarra2002). The result can be found in Figure 2, evidencing a very good agreement theory-PIC.
Fig. 2. Comparison of the shock formation time given by the theory with the results of PIC simulations.
At this junction, it is interesting to compare the shock formation time in pair and electron–proton plasmas. From Eqs (2) and (5), we get (Bret et al., Reference Bret, Stockem, Fiúza, Ruyer, Gremillet, Narayan and Silva2013),
$$\displaystyle{{{{\rm \tau} _{{\rm f,ep}}}} \over {{{\rm \tau} _{{\rm f,pairs}}}}} = \displaystyle{{6.2} \over \Pi} \ln \displaystyle{{{m_{\rm p}}} \over {{m_{\rm e}}}}\sqrt {\displaystyle{{{m_{\rm p}}} \over {{m_{\rm e}}}}}, $$where Π ~ 10–20, is the number of exponentiations of the electronic Weibel instability. The function so defined is plotted in Figure 3 in terms of Π and m p/m e. For a mass ratio of 1836, a shock in electron–proton plasmas requires 100–200 more time to form than in pair plasmas.
Fig. 3. Plot of Eq. (6) in terms of m p/m e and Π. For a mass ratio of 1836, a shock in electron–proton plasma takes 100–200 more time to form than in pair plasmas.
4. RANKINE–HUGONIOT
As evidenced previously, our determination of the shock formation hinges on the validity of the RH jump condition. Within the relativistic regime where we operate, the expected RH density jump is 3 in 2D and 4 in 3D (Stockem et al., Reference Stockem, Fiúza, Fonseca and Silva2012). To which extent should we expect its fulfilment for a collisionless shock?
These density jumps rely on the conservation of matter, momentum and energy across the shock front. If matter carries all the energy and momentum, then these jumps are correct, provided all the matter upstream goes downstream. In a collisionless chock, this latter assumption may be challenged, for at least two reasons:
1. With a mean-free path much larger than the shock front, some particles may bounce back from the upstream, or even come back upstream from the downstream (the shock front only goes at c/2 in 2D and c/3 in 3D).
2. Collisionless shocks are known to accelerate particles and grow a high-energy, non-Maxwellian tail (Krymskii, Reference Krymskii1977; Spitkovsky, Reference Spitkovsky2008). These high-energy particles may go back and forth near the shock front, before escaping upstream or downstream.
In either case, part of the initial upstream energy and momentum escapes the RH budget, blurring the jump condition. Regarding the accelerated particles, the high-energy tail grows with time like 
$\sqrt t $, gathering more and more energy (Sironi et al., Reference Sironi, Spitkovsky and Arons2013). As a result, downstream temperatures of only 80% of the RH one have been observed in simulations (Caprioli & Spitkovsky, Reference Caprioli and Spitkovsky2014).
However, the present chock formation time relies, by definition, on the RH density jump at the very beginning of the shock history. At this stage, no particles have been accelerated yet, and we are left with the first population above. To our knowledge, there is no theory of the amount of particles departing from a pure “upstream → downstream” trajectory. For the pair case, numerical explorations of this problem found that the deviation from the RH expected jump is initially of the order of the spontaneous density fluctuations behind the front (Stockem et al., Reference Stockem, Fiúza, Fonseca and Silva2012).
5. CONCLUSION
We have presented a theory for the formation of a collisionless Weibel shock, both in pair and electron/proton plasmas. The setup investigated consists in the generation of a shock from the encounter of two identical, cold, relativistic and un-magnetized plasma shells.
When the two shells start overlapping, the overlapping region turns unstable to the Weibel instability. A key concept related to the formation scenario is the one of trapping time τp, which is the time at which the instability-generated turbulence in the overlapping region is able to trap the incoming flow. Once trapping have been achieved, the shock formation time is simply 2τp in 2D, and 3τp in 3D, namely dτp where d is the dimension of the problem.
For pair plasmas, the trapping time equals the saturation time τs of the Weibel instability. By the time Weibel saturates, the magnetic filaments and the peak field are large enough to efficiently trap the incoming flow in the central region. Shock formation ensues at 2τp or 3τp, depending of the geometry.
For electron/proton, the scenario leading to the shock formation is significantly longer. As the two plasma shells overlap, electrons turn Weibel unstable first. When this instability saturates, it has seeded an unstable mode that is further grown by the proton Weibel instability. This later instability then saturates in turn, but the filaments it grew are too small to trap the incoming ion flow. We must then wait for the filaments to merge, until they are big enough to trap the ion flow. This is when the trapping time τp is reached. As was the case for the pair plasmas, shock formation follows at 2τp or 3τp, depending of the geometry. Equations (2) and (5) for the shock formation time in pair and electron/proton plasmas have been successfully checked by means of PIC simulations.
The ratio of the formation time in pair to the formation time in electron/proton plasmas is an interesting quantity, in particular when it comes to designing an experiment aiming at producing such shocks in the lab. Depending on the number of exponentiations of the electronic Weibel instability, and for a realistic proton to electron mass ratio, Eq. (6) shows that a shock in electron/proton plasmas requires 100–200 more time to form than in pairs. This, in turn, translates into the interaction length required between the two shells.
Although more work would be needed to determine more precisely the range of application of the RH jump conditions, simulations show they are tightly fulfilled at the beginning of the shock history. The reason for this is that the high-energy tail the shock grows with time, has not developed yet. Future woks may also contemplate the effect of a non-zero temperature in the shells before they collide, or that of an external magnetic field.
ACKNOWLEDGMENTS
This work was supported by the European Research Council (ERC-2010-AdG grant 267841), by grant ENE2013-45661-C2-1-P from the Ministerio de Educación y Ciencia, Spain, and grant PEII-2014-008-P from the Junta de Comunidades de Castilla-La Mancha. The authors acknowledge the Gauss Centre for Supercomputing (GCS) for providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS share of the supercomputer JUQUEEN at Jülich Supercomputing Centre (JSC).
