1. INTRODUCTION
Recently, much interest has focused on studying the interaction of
high-intensity laser pulses with clusters because they may bridge the
gap between a molecular and solid state of matter. In 1993, McPherson
et al. first observed anomalous X-ray line emission from
highly charged Kr and Xe ions when a high intensity 248-nm laser was
focused on Kr and Xe clusters (McPherson et
al., 1993). Since then, many other groups, including Lezius
et al. (1998), Rose-Petruck et
al. (1997), and Ditmire et al.
(1995, 1996, 1997a, 1997b,
1998) have studied various aspects of the
interaction of clusters with high-intensity femtosecond laser pulses. Many
studies have shown that clusters absorb the energy of laser pulses very
efficiently (Ditmire et al.,
1997a). Very bright X-ray emission in the 100–5000 eV
range (Ditmire et al., 1995; Zweiback et al., 1999), extremely energetic ions
with energy up to 1 MeV (Ditmire et al., 1997b, 1998), and keV
electrons (Shao et al., 1996) were observed
in these experiments. And it is very exciting that DD nuclear fusion was
produced when Ditmire et al. drove explosions in deuterium clusters
with a 35-fs laser pulse (Zweiback et al.,
2000).
Until now, several different theoretical models (McPherson et al., 1993; Ditmire et al., 1996; Rose-Petruck et al., 1997; Last & Jortner, 1998) have been developed to
explain these observations. In these models, the nanoplasma model (also
called the hydrodynamic model) is a better one for large clusters in a
high-intensity laser field. In this model, each cluster was treated as
a small ball of high-density plasma and the cluster size is large
enough to confine the majority of electrons to the cluster region. The
cluster was heated by field ionization, collisional ionization, and
inverse bremsstrahlung heating. This theory can explain many
experimental phenomena, such as the expansion process of the clusters,
the production of highly charged and high-energy ions, the observation
of highly energetic electrons, and especially the resonance
absorption.
However, the nanoplasma model does not give us a detailed description
near the resonance point and seems to overestimate the enhancement of
the electric field inside the clusters at the resonance point. With
some experimental parameters (Liu et al.,
2001), the electric field inside the clusters will be enhanced
to hundreds of times that in vacuum. If the resonance point occurs
exactly at the peak intensity of the laser pulse, for example,
1016 W/cm2, the intensity of the electric
field inside the cluster will increase to 1021
W/cm2. Such a high electric field can directly produce
highly charged ions such as Kr28+ by optical field
ionization (OFI), but none of them has been observed in experiments.
Moreover, the average ion energy calculated from this model is much
higher than experimental results (Ditmire et
al., 1996).
To get more reasonable explanations, a modified nanoplasma model has
been proposed by Liu et al. (2001),
which is reasonable for explaining the generation of highly charged
ions and the mean kinetic energy of ions in the interactions of large
clusters with high-intensity femtosecond laser pulses. In this article,
this model has been employed to investigate the scaling of charge
states and mean kinetic energy of ions with cluster and laser
parameters in laser–cluster interactions. To make it comparable
to our experimental works (Li et al.,
2000) and give theoretical explanations for our further
experiments, our investigations will be aimed at Ar clusters.
2. CALCULATION MODEL
A detailed description of the modified nanoplasma model has been
given in Liu et al. (2001). Here we
will only describe the modified model briefly. In the original
nanoplasma model (Ditmire et al.,
1996), the cluster is approximately treated as a uniform small
ball of plasma that is much smaller than the wavelength of the laser,
so the field distribution in the cluster can be also treated as
uniform. The electric field in the cluster is given by E =
3E0 /|ε + 2|,
E0 is the electric field in vacuum. The plasma
dielectric constant derived from the Drude model is ε = 1 −
ωp2/ω(ω +
iν), where
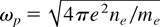
is the plasma
frequency, ν is the electron–ion collision frequency, and
ω is the laser frequency. At the resonance point when the electric
density decreases to 3ncrit, the electric
field and the heating rate inside the cluster are evidently enhanced,
which leads to a rapid increase in the electron temperature and the
expansion velocity of the cluster. Therefore at the resonance point,
the quasistatic plasma dielectric constant may not be suitable any
longer because the electron density and temperature change so rapidly.
In our modified nanoplasma model, by solving the Maxwell equations, we
defined an effective plasma dielectric constant
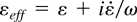
to replace the quasistatic
one. When the change rate of ε is comparable to
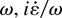
may reach a considerably large
value, and therefore weaken the enhancement of the electric field
inside the clusters, and a reasonable explanation can be obtained.
The modified nanoplasma model can be described by the following
equations:
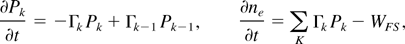
Γk = Wtun +
We, where WFS
is the rate of OFI, WFS is the rate of
electron-impact ionization, WFS is the
escape rate of electrons, ne is the
electron density, and Pk is the density of
the ions of charge state k(k =
0,1,2,…).
where Pcoul =
(Q2e2)/(8πr4)
is Coulomb pressure, Pe =
nKTe is the electron thermal pressure,
r is the radius of the expanding cluster,
ni is the ion density, and
mi is the ion mass.
where qFS is the energy loss caused
by the hot electrons that escape from the cluster,
∂U/∂t is the laser energy deposition
rate inside the cluster, and
(3/r)Pe∂r/∂t
is the work associated with the expanding cluster.
Because a uniform expanding process is assumed in this model, the ion
radial velocity increases linearly along with its distance from the
center in the cluster; the mean kinetic energy of Ar ions will be
calculated as
where mi =
40mp (mp is
the mass of a proton) is the mass of Ar ions and
vi is the cluster expansion velocity.
Employing the model, the dynamics of Ar clusters with high-intensity
femtosecond lasers has been simulated.
3. CALCULATIONS
Figure 1 shows the simulated process of a
5.5-nm (3000 atoms) Ar cluster illuminated by a 780-nm, 150-fs laser
pulse at a peak intensity of 1.5 × 1016
W/cm2. The ion fraction from Ar5+ to
Ar10+ and laser pulse envelop as a function of time are
shown in Figure 1a; the average charge of Ar
ions is about 8.5+. The expanding velocity of the cluster and the mean
ion energy calculated from the expanding velocity by Eq. (1) as
functions of time are shown in Figure 1b; the
calculated mean kinetic energy of ions is about 17 keV, which is very
close to our experimental results (Li et
al., 2000).
Ar ion fraction from Ar5+ to Ar10+ (a) and
laser pulse envelop (b) expanding velocity of cluster and mean kinetic
energy of ions as functions of time for a 5.5-nm (3000 atoms) Ar
cluster driven by a 780-nm, 150-fs, 1.5 × 1016
W/cm2 laser pulse.
Figure 1 demonstrates a sudden increase of
Ar8+ production and a great enhancement of the mean ion
energy. These are obviously the results of resonance absorption. In
experiments, the resonance point can be controlled through the
adjustment of laser and cluster parameters, so we can optimize the
cluster explosion to get more energetic and higher charged ions. In the
following section, we will present the theoretical investigations of
the scaling of the mean kinetic energy and charge states of Ar ions
produced from laser-irradiated Ar clusters as functions of cluster size
and laser intensity.
3.1 Cluster size dependence
In Figure 1, the resonance point arrives
later than the peak intensity of the laser pulse. It may be inferred
that for a smaller cluster, it expands rapidly, and this point occurs
closer to the peak intensity of the laser pulse; therefore the coupling
efficiency of the laser energy will be increased. But for a much
smaller cluster, the resonance point comes earlier than the peak
intensity of the laser pulse and decreases the energy coupling
efficiency. On the other hand, a larger cluster expands slowly, so this
point comes much later than the peak intensity of the laser pulse and
will also lead to a decrease of energy coupling efficiency. So there
should be an optimum cluster size for given laser parameters, where the
best absorption efficiency of the laser energy can be obtained.
Figure 2a shows the mean kinetic energy of
Ar ions scaling with the cluster sizes for 780-nm, 150-fs laser pulses
at different peak intensities. Optimum sizes of cluster can obviously
be obtained in the figure: When the peak intensity of the laser is 1.5
× 1016 W/cm2, the optimum cluster size
is about 7.0 nm in diameter (about 7000 Ar atoms); however, it is 8.0
nm (about 9000 Ar atoms) when the peak intensity is 2.0 ×
1016 W/cm2. The increase of laser intensity
also increases the initial ionization and expansion rates, and the
resonance point will occur earlier in the laser pulse; therefore the
optimum size will shift toward larger clusters.
Mean kinetic energy (a) and average charge state of Ar ions (b) with
varieties of cluster sizes when Ar clusters are irradiated by laser
pulses with different intensities (1.5, 2.0 × 1016
W/cm2). The laser pulse length is 150 fs and the laser
wavelength is 780 nm.
The average charge state of Ar ions is also calculated and shown in
Figure 2b. We can see that the charge state
of Ar ions increases linearly with the cluster size: The larger the
cluster size, the higher the charge state of Ar ions. This can be
explained by the ionization process where the electron-impact
ionization dominates. In the early time of interaction, the electron
density increases to a ultrahigh level due to optical field ionization.
The electrons are heated by inverse bremsstrahlung and the electron
temperature also increases. So, the rate of electron-impact ionization
is very large. For a larger size cluster, the heating and
electron-impact ionization occur for a longer time, so higher charge
states are produced.
3.2. Scaling with laser intensity
We have already seen that a higher intensity of laser pulse will
bring forward the resonance point. Like the scaling with cluster size,
an optimum intensity of the laser pulse may exists for a given cluster
size, where a best absorption efficiency of the laser energy can be
obtained. In Figure 3, the mean kinetic
energy and average charge state of ions, together with energy
absorption efficiency for several laser intensities and given cluster
sizes of 4.0 nm (thin lines) and 5.5 nm (thick lines), are shown. The
intensities are from 1015 W/cm2 to
1017 W/cm2, which are accessible in our
experiments. Irradiated by laser pulses with these intensities, the
electron density will increase to a much higher value than
3ncrit in a short time, due to field
ionization, and then fall through 3ncrit
before the laser pulse vanishes; that is, the resonance absorption
occurs within the laser pulse.
Mean kinetic energy of ions (a), average charge state of ions (b),
and energy absorption efficiency (c) with varieties of laser
intensities. The laser pulse length is 150 fs and the laser wavelength
is 780 nm.
In Figure 3, the mean kinetic energy of Ar
ions and its average charge state from different-size clusters increase
with the laser intensity, and at particular intensities (1.1 ×
1017 W/cm2 for 4.0-nm Ar cluster and 1.2
× 1017 W/cm2 for 5.5 nm), they rise
rapidly then fall down. These lines clearly demonstrate the effect of
resonance absorption in laser–cluster interactions.
Because higher intensity will also increase the absolute value of ion
energy, the mean kinetic is not suitable for investigating the coupling
efficiency of laser–cluster interactions. A simple energy
absorption efficiency e =
E/Ipeak
(E is the mean energy of ions and
Ipeak is the peak intensity of laser
pulse) is used to solve this problem; its scaling against laser
intensity is shown in Figure 3c. Because of
the saturation of energy absorption, the energy absorption efficiency
is lower for much higher intensities. For a 4.0-nm in diameter cluster,
a laser pulse with intensity 2 × 1015
W/cm2 occurs at the maximum energy absorption
efficiency, and for a 5.5-nm cluster, the corresponding intensity is 3
× 1015 W/cm2. However, in the vicinity
of resonance absorption, the energy absorption will obviously be
enhanced because of the resonance.
4. CONCLUSION
In our calculations, the mean kinetic ion energy is very close to our
observed results; but in Ditmire et al. (1996), the calculated kinetic ion energy is close
to the maximum ion energy of experimental measurements. The cause might
be that the original nanoplasma model overestimates the resonance
enhancement. By use of an effective dielectric constant, the modified
nanoplasma model is very suitable for investigating the high-energy
ions exploded from laser–cluster interactions.
In conclusion, the modified nanoplasma model is used to simulate the
interaction between Ar clusters and high-intensity femtosecond laser
pulses. The calculated mean ion energies are in good agreement with our
experimental results. For our further experiments, we are investigating
the scaling of the mean kinetic energy and the charge state of Ar ions
with cluster size and laser intensity. An optimum cluster size for a
given laser pulse, together with an optimum laser intensity for a given
cluster size, are found because of the mechanism of the resonance
absorption.
