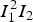1. INTRODUCTION
Terahertz (THz) radiation generation has attracted a lot of attention in recent years because of its potential applications in imaging (Jackson et al., Reference Jackson, Mourou, Whitaker, Duling, Williamson, Menu and Mourou2008; Reference Jackson, Bowen, Walker, Labaune, Mourou, Menu and Fukunaga2011), remote sensing (Antonsen et al., Reference Antonsen, John and Milchberg2007), chemical, and security identification (Shen et al., Reference Shen, Lo, Taday, Cole, Tribe and Kemp2005). From the view of generation mechanisms, several different theories have already been proposed such as four-wave mixing (Cook & Hochstrasser, Reference Cook and Hochstrasser2000; Xie et al., Reference Xie, Dai and Zhang2006), mode conversion (Sheng et al., Reference Sheng, Mima, Zhang and Sanuki2005), transient current model (Kress et al., Reference Kress, Löffler, Eden, Thomson and Roskos2004; Kim et al., Reference Kim, Glownia, Taylor and Rodriguez2007; Wu et al., Reference Wu, Meyer-Ter-vehn and Sheng2008; Chen et al., Reference Chen, Pukhov, Peng and Willi2008; Reference Chen, Yuan and Sheng2012; Li et al., Reference Li, Li, Zhou, Wang, Du, Ding, Lin, Liu, Sheng, Peng, Chen, Ma, Lu, Wang, Wei and Zhang2012), and quantum mechanical model (Karpowicz & Zhang, Reference Karpowicz and Zhang2009). From the view of experimental and theoretical studies, THz radiation can come from one-color (Tzortzakis et al., Reference Tzortzakis, Méchain, Patalano, Andre′, Prade, Franco, Mysyrowicz, Munier, Gheudin, Beaudin and Encrenaz2002; Sprangle et al., Reference Sprangle, Peñano, Hafizi and Kapetanakos2004; Chen et al., Reference Chen, The′BERGE, Kosareva, Panov, Kandidov and Chin2007; D'amico et al., Reference D'amico, Houard, Franco, Prade, Mysyrowicz, Couairon and Tikhonchuk2007; Hu et al., Reference Hu, Shen, Lei, Li and Xu2010; Wu et al., Reference Wu, Meyer-Ter-vehn, Ruhl and Sheng2011; Matsubara et al., Reference Matsubara, Nagai and Ashida2012; Zhao et al., Reference Zhao, Zhang, Wang, Chu, Zeng, Liu and Xu2014) and two-color (Zhong et al., Reference Zhong, Karpowicz and Zhang2006; Peñano et al., Reference Peñano, Sprangle, Hafizi, Gordon and Serafim2010; Wang et al., Reference Wang, Daigle, Yuan, The′berge, Châteauneuf, Dubois, Roy, Zeng and Chin2011; Reference Wang, Tong Li, Sheng, Lu and Zhang2013; You et al., Reference You, Oh and Kim2012; Oh et al., Reference Oh, You, Jhajj, Rosenthal, Milchberg and Kim2013; Varshney et al., Reference Varshney, Sajal, Baliyan, Sharma, Chauhan and Kumar2013a; Reference Varshney, Sajal, Singh, Kumar and Sharma2013b; Reference Varshney, Sajal, Chauhan, Kumar and Sharma2014; Yang & Du, Reference Yang and Du2013; Zhao et al., Reference Zhao, Chu, Guo, Wang, Yang, Liu, Cheng and Xu2013) laser–gas interactions. These filaments generation and THz radiation have gained special attention because of the relative simplicity of the experimental operation.
THz radiation from one-color laser–gas interaction has been studied by various groups. D'Amico et al. (Reference D'amico, Houard, Franco, Prade, Mysyrowicz, Couairon and Tikhonchuk2007) have reported the emission of strongly collimated THz beam in the forward direction from the plasma filament and Tzortzakis et al. (Reference Tzortzakis, Méchain, Patalano, Andre′, Prade, Franco, Mysyrowicz, Munier, Gheudin, Beaudin and Encrenaz2002) have observed the emission of THz radiation from the plasma filament in the direction perpendicular to the laser propagation axis. Peñano et al. (Reference Peñano, Sprangle, Hafizi, Gordon and Serafim2010) have given a detailed analysis of THz emission from the plasma filament. They found that in the spatially modulated medium the ponderomotive force has superluminal Fourier components, which is responsible for the THz emission.
Similarly, for two-color laser gas interaction, Cook & Hochstrasser (Reference Cook and Hochstrasser2000) first reported their THz emission experimental results. They have noted that the four-wave mixing due to third-order nonlinearity in air is responsible for THz generation. Oh et al. (Reference Oh, You, Jhajj, Rosenthal, Milchberg and Kim2013) have studied THz generation from the gaseous and clustered plasma. Their experimental observations confirm scalable THz generation with increasing filament length. Similarly, You et al. (Reference You, Oh and Kim2012) have observed phase-matched THz generation from two-color laser and obtained considerable increase in yield with filament length. Matsubara et al. (Reference Matsubara, Nagai and Ashida2012) have reported ultra-broadband radiation up to 200 THz via two-color laser mixing. Other possible mechanisms have also been proposed to explain the THz generation from two-color laser gas interaction. Transient photocurrent model developed by Kim et al. (Reference Kim, Glownia, Taylor and Rodriguez2007), use symmetry-broken laser field to excite coherent THz emission from air. Klarskov et al. (Reference Klarskov, Strikwerda, Iwaszczuk and Jepsen2013) have studied the three-dimensional intensity profile emitted from a two-color air plasma. They have reported that the nonlinear optical response of the plasma and the transient photocurrents result in emission of a conical beam of THz radiation.
In this paper, we propose and discuss another possible mechanism for THz radiation generation via two-color laser pulses interaction in a collisional plasma. The physical mechanism of THz generation is different from the above two-color transient photocurrent model. In our case, the THz generation current is not due to ionization-induced electrons’ residual momentum; however, it is due to the electric current generated by the ponderomotive force of the two-color beat wave in the plasma. The THz generation process is as follows: An intense short laser pulse with frequency ω1 and wave number k 1 is mixed with its frequency-shifted second harmonic with frequency ω2 and wave number k 2, where ω2 = 2ω1 + ωT, ωT is in the THz range, in the plasma. The lasers exert a ponderomotive force on the electrons and drive density perturbations at (2ω1, 2k 1) and (ω2− ω1, k 2− k 1). These density perturbations couple with the oscillatory velocities of the electron due to the lasers and produce a nonlinear current density at (ω2− 2ω1, k 2 − 2k 1) and generate the p-polarized electromagnetic wave radiation. The paper is organized as follows: In Sections 2 and 3, we calculate the nonlinear current density including the collisional effects and obtain far-field THz emission. In Section 4, two-dimensional particle-in-cell (2D-PIC) simulation is carried out to study the near-field radiation properties and the conclusion is given in Section 5.
2. NONLINEAR CURRENT DENSITY
As shown in Figure 1, we consider two-color pulse propagation in the plasma with frequency ω1 and wave vector 
${\vec k}_1$, represented by the field
$${\vec E}_1 = \hat x{{\rm A}_{{\rm 10}}}\,{e^{ - {r^2}/2R_0^2}} \,{e^{ - i\left({{\rm \omega} _1}t - {k_1}z\right)}},$$
and its frequency-shifted second harmonic of frequency ω2 and wave vector 
${\vec k}_2$,
$${\vec E}_2 = \hat x{{\rm A}_{{\rm 20}}}\,{e^{ - {r^2}/2R_0^2}} \,{e^{ - i\left({{\rm \omega} _2}t - {k_2}z\right)}},$$
where ω2 = 2ω1 + ωT, ωT is in the THz range in the plasma, 
${k_1} = \left({{\rm \omega} _1}/c\right)\sqrt {1 - {\rm \omega} _{\rm p}^2 /{\rm \omega} _1^2} $, 
${k_2} = \left({{\rm \omega} _2}/c\right)\sqrt {1 - {\rm \omega} _{\rm p}^2 /{\rm \omega} _2^2}\comma $ and 
${{\rm \omega} _{\rm p}} = \sqrt {{n_0}{e^2}/m{{\rm \varepsilon} _0}} $ is the plasma frequency, n 0 is the electron density, and R 0 is the initial laser spot size. –e and m are the charge and mass of the electron, respectively. The polarization of the lasers are kept same (x-axis) to obtain the maximum current density.
Fig. 1. Schematic representation of THz radiation when two color laser pulses propagate in air plasma.
Using the equation of motion 
$\left(\partial /\partial t + {\rm \nu}\right){\vec v} = - (e/m){\vec E}$, the oscillatory velocities of the electrons due to the lasers are obtained as
$${\vec v}_{{{\rm \omega} _1}} = \displaystyle{{e{{\vec E}_1}} \over {mi{{\rm \omega} _1}\left(1 + i{\rm \nu} /{{\rm \omega} _1}\right)}},$$
$${\vec v}_{{{\rm \omega} _2}} = \displaystyle{{e{{\vec E}_2}} \over {mi{{\rm \omega} _2}\left(1 + i{\rm \nu} /{{\rm \omega} _2}\right)}},$$where ν is the collision frequency.
The ponderomotive force exerted on the electrons at (2ω1, 2k 1) and (Δω, Δk) are
$${\vec F}_{{{\rm P}_{\left(2{{\rm \omega} _1}\right)}}} = - e{\vec v}_{{{\rm \omega} _1}} \times {\vec B}_{{{\rm \omega} _1}} = - \displaystyle{{{e^2}{k_1}E_1^2} \over {2mi{\rm \omega} _1^2 \left(1 + i{\rm \nu} /{{\rm \omega} _1}\right)}}\hat z,$$
$$\eqalign{{{\vec F}_{{{\rm P}_{\Delta {\rm \omega}}}}} & = - e\left({{\vec v}_{{{\rm \omega} _2}}} \times {\vec B}_{{{\rm \omega} _1}}^{\ast} + {\vec v}_{{{\rm \omega} _1}}^{\,\ast} \times {{\vec B}_{{{\rm \omega} _2}}}\right) \cr & = \displaystyle{{{e^2}\Delta k\left({{\vec E}_2}.{\vec E}_1^{\ast} \right)} \over {2mi{{\rm \omega} _1}{{\rm \omega} _2}}}\left(1 + i{\rm \nu} /{\rm \varpi} \right)\hat z,} $$
where 
${\varpi} = {{\rm \omega} _1}{{\rm \omega} _2}\Delta k/{{\rm \omega} _2}{k_2} + {{\rm \omega} _1}{k_1}$, Δω = ω2 − ω1, and Δk = k 2 − k 1.
The oscillatory velocity of the electrons at (2ω1, 2k 1) due to the ponderomotive force 
${\vec F}_{{\rm P}_{2{\rm \omega}_1}}\left({ = e\nabla {\rm \phi}_{{\rm p}(2{\rm \omega}_1)}}\right)$ and self-consistent field 
$\left({\vec E}_{2{{\rm \omega} _1}} = - \nabla {{\rm \phi} _{{\rm s}\left(2{{\rm \omega} _1}\right)}} \right)$, is on solving the equation of motion,
$$(\partial /\partial t + {\rm \nu} ){\vec v}_{2{{\rm \omega} _1}} = \displaystyle{e \over m}\nabla \left({{\rm \phi} _{s\left(2{{\rm \omega} _1}\right)}} + {{\rm \phi} _{\,p\left(2{{\rm \omega} _1}\right)}}\right),$$turns out to be,
$${\vec v}_{2{\rm \omega} _1} = - \displaystyle{{e \nabla \left({{\rm \phi}_{{\rm s}(2{\rm \omega}_1)} + {\rm \phi} _{{\rm p}(2{\rm \omega}_1)}}\right)} \over {2im{\rm \omega}_1\left(1 + i{\rm \nu} /2{\rm \omega}_1\right)}},$$
where 
${\rm \phi} _{{\rm p}\left(2{\rm \omega}_1\right)} = eE_1^2 /4m{\rm \omega} _1^2 \left(1 + i{\rm \nu} /{\rm \omega}_1\right)$. The velocity 
${\vec v}_{2{{\rm \omega} _1}}$, gives rise to density oscillation at frequency (2ω1), which on solving the equation of continuity 
$(\partial /\partial t){n_{2{{\rm \omega} _1}}} + \nabla \cdot \left({n_0}{\vec v}_{2{{\rm \omega} _1}}\right) = 0$, turns out to be,
$$n_{2{\rm \omega}_1} = \displaystyle{{n_0e{\nabla}^2 \left({{\rm \phi}_{{\rm s}(2{\rm \omega}_1)} + {\rm \phi} _{{\rm p}(2{\rm \omega}_1)}}\right)} \over {4{\rm \omega}_1^2 m\left(1 + i{\rm \nu} /2{\rm \omega}_1\right)}}.$$
Substituting Eq. (9) into Poisson's equation, 
${\nabla ^2}{{\rm \phi} _{{\rm s}\left(2{{\rm \omega} _1}\right)}} = {n_{2{{\rm \omega} _1}}}e/{{\rm \varepsilon} _0}$, one obtains, 
${\rm \phi} _{{\rm s}(2{\rm \omega}_1)} = \left({\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right) / \left(1 + i{\rm \nu} /2{\rm \omega}_1 -{\rm \omega}_{\rm p}^2 /4{\rm \omega} _1^2 \right){\rm \phi}_{{\rm p}(2{\rm \omega}_1)}$. Hence, the perturbed velocity and density modifies to,
$${\vec v}_{2{{\rm \omega} _1}} = - \displaystyle{{{e^2}{k_1}E_1^2} \over {4{m^2}{\rm \omega} _1^3}} \displaystyle{1 \over {\left(1 + i{\rm \nu} /{{\rm \omega} _1}\right)\left[1 + i{\rm \nu} /2{{\rm \omega} _1} - \left({\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right) \right]}}\hat z,$$
$${n_{2{{\rm \omega} _1}}} = - \displaystyle{{{n_0}{e^2}k_1^2 E_1^2} \over {4{m^2}{\rm \omega} _1^4}} \displaystyle{1 \over {\left(1 + i{\rm \nu} /{{\rm \omega} _1}\right) \left[1 + i{\rm \nu} /2{{\rm \omega} _1} - \left({\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)\right]}}.$$
Similarly, the ponderomotive force 
${\vec F}_{{{\rm P}_{\Delta {\rm \omega}}}}$ gives rise to oscillatory velocity to the electrons 
${\vec v}_{\left(\Delta {\rm \omega}, \Delta k\right)}$ and drives the density perturbation
$${n_{{\kern 1pt} \left(\Delta {\rm \omega}, {\kern 1pt} \Delta k\right)}} = \displaystyle{{{n_0}{e^2}\Delta {k^2}\left({{\vec E}_2}.{\vec E}_1^{\ast} \right)} \over {2{m^2}{{\rm \omega} _1}{{\rm \omega} _2}\Delta {{\rm \omega} ^2}}}\displaystyle{{\left(1 + i{\rm \nu} /{\rm \varpi} \right)} \over {\left(1 + i{\rm \nu} /\Delta {\rm \omega} - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}}.$$
Hence, the total nonlinear current density at [
${{\rm \omega} _{\rm T}}\left( = {{\rm \omega} _2} - 2{{\rm \omega} _1}\right)$, 
${k_{\rm T}}\left( = {k_2} - 2{k_1}\right)$] is
$$\eqalign{ {\vec J}_{({\rm \omega} ,k)}^{\;{\rm NL}} & = - \displaystyle{e \over 2}n_{2{{\rm \omega} _1}}^{\ast} {{\vec v}_{{{\rm \omega} _2}}} - \displaystyle{e \over 2}{n_{{\rm \Delta} {\rm \omega}}}{\vec v}_{{{\rm \omega}_1}}^{\ast} \cr & = {J_0}{\mkern 1mu} {e^{ - 3{r^2}/2R_0^2 }}{e^{ - i({{\rm \omega} _{\rm T}}t - {k_{\rm T}}z)}}\hat x,} $$
where 
${J_0} = - i\left({n_0}ec/8\right){a_{20}}a_{10}^2 \left(1 + i{\rm \nu} /{{\rm \omega} _1}\right)\left( {{{\rm \alpha} _1} + i{{\rm \alpha} _2}} \right)\comma\; {a_{10}} = $
$e{A_{10}}/m{{\rm \omega} _1}c$, and 
${a_{20}} = e{A_{20}}/m{{\rm \omega} _2}c$,
$$\eqalign{{{\rm \alpha} _1} & = \displaystyle{{k_1^2 {c^2}/{\rm \omega} _1^2} \over {\left(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)}}\displaystyle{{{{\left(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)}^2}} \over {{{\left(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)}^2} + {{\rm \nu} ^2}/4{\rm \omega} _1^2}} \cr & \quad \left[ {1 + \displaystyle{{{{\rm \nu} ^2}} \over {2{{\rm \omega} _1}{{\rm \omega} _2}\left(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)}}} \right] \cr & \quad + 2{\left( {\displaystyle{{\Delta kc} \over {\Delta {\rm \omega}}}} \right)^2}\displaystyle{1 \over {\left(1 - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}} \cr & \quad \left[ {1 + \displaystyle{{{{\rm \nu} ^2}} \over {\Delta {\rm \omega} {\rm \varpi} \left(1 - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}}\displaystyle{{{{\left(1 - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}^2}} \over {{{\left(1 - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}^2} + {{\rm \nu} ^2}/\Delta {{\rm \omega} ^2}}}} \right],}$$and
$$\eqalign{{{\rm \alpha} _2} & = \displaystyle{{\rm \nu} \over {{{\rm \omega} _1}}}\left[ {\displaystyle{{k_1^2 {c^2}/{\rm \omega} _1^2} \over {\left(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)}}\left( {\displaystyle{1 \over {2\left(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)}} + \displaystyle{{{{\rm \omega} _1}} \over {{{\rm \omega} _2}}}} \right)} \right. \cr & \quad \displaystyle{{{{\left(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)}^2}} \over {{{\left(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)}^2} + {{\rm \nu} ^2}/4{\rm \omega} _1^2}} \cr & \quad + 2{\left( {\displaystyle{{\Delta kc} \over {\Delta {\rm \omega}}}} \right)^2}\displaystyle{{{{\rm \omega} _1}/{\rm \varpi}} \over {\left(1 - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}} \cr & \quad \left. {\left( {1 - \displaystyle{{\rm \varpi} \over {\Delta {\rm \omega} \left(1 - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}}\displaystyle{{{{\left(1 - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}^2}} \over {{{\left(1 - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}^2} + {{\rm \nu} ^2}/\Delta {{\rm \omega} ^2}}}} \right)} \right].}$$ If one takes, 
${\rm \nu} /{{\rm \omega} _1} \ll 1$, Eq. (13) reduces to,
$${\vec J} = - i\displaystyle{{{n_0}ec} \over 8}{a_{20}}a_{10}^2 {{\rm \alpha} _1}\,{e^{ - 3{r^2}/2R_0^2}} {e^{ - i\left({{\rm \omega} _{\rm T}}t - {k_{\rm T}}z\right)}}\hat x,$$
where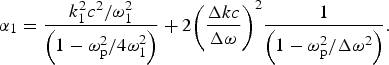 
${{\rm \alpha} _1} = \displaystyle{{k_1^2 {c^2}/{\rm \omega} _1^2} \over {\left(1 - {\rm \omega} _{\rm p}^2 /4{\rm \omega} _1^2 \right)}} + 2{\left( {\displaystyle{{\Delta kc} \over {\Delta {\rm \omega}}}} \right)^2}\displaystyle{1 \over {\left(1 - {\rm \omega} _{\rm p}^2 /\Delta {{\rm \omega} ^2}\right)}}.$ The two terms in the above equation is because of the density fluctuations at 2ω1 and 
$\Delta {\rm \omega} = {{\rm \omega} _2} - {{\rm \omega} _1},$ respectively.
3. THz GENERATION AS AN ANTENNA
The retarded vector potential at a far point 
${\vec r}(r,{\rm \theta}, z)$ due to the current density in the filament of length L and radius r f is given as
$${\vec A}(r,{\kern 1pt} t) = \displaystyle{{{{\rm \mu} _0}} \over {4{\rm \pi}}} \int \displaystyle{{\vec J}\left(r^{\prime},{\kern 1pt} t - R/c\right) \over R}{d^3}V^{\prime},$$
where 
$R = \left\vert r - r^{\prime} \right\vert$ and the volume integral is over the entire length and cross-section of the filament. As the filament radius is less than the THz wavelength, ponderomotive force-driven current can be taken to be unmodified by the self-field and the nonlinear current source can be treated like a wire antenna as far as the radiation field is concerned. Hence, for the filament of radius 
${r_{\rm f}} \ll c/{{\rm \omega} _{\rm T}}$, the nonlinear current density can be written as
$${\vec J}^{{\rm NL}} = {J_0}\,{e^{ - 3{{r^{\prime}}^2}/2R_0^2}} \,{e^{ - i \left[{{\rm \omega} _{\rm T}}(t - r/c) - {{\rm \omega} _{\rm T}}z^{\prime}(1 + (3{{\rm \omega} _{\rm p}}/4{{\rm \omega} _1}) - {\rm cos}{\rm \theta} )/c \right]}}\hat x,$$
where 
${k_{\rm T}}\left( = {k_2} - 2{k_1}\right) \approx {{\rm \omega} _{\rm T}}/c \left[1 + \left(3{{\rm \omega} _{\rm p}}/4{{\rm \omega} _1}\right)\right]$ and 
$R \approx r - z^{\prime} \cos {\rm \theta} $ are used. Here θ is the angle between r- and z-axes (Fig. 1). Using Eq. (17) in (16), one gets
$$\eqalign{& {\vec A}(r,{\kern 1pt} t) = \hat x\displaystyle{{{{\rm \mu} _0}{J_0}\,{e^{ - i{{\rm \omega} _{\rm T}}(t - r/c)}}} \over {4{\rm \pi}}} \cr & \quad \int_0^L {\int_0^{2{\rm \pi}} {\int_0^{{r_{\rm f}}} \displaystyle{{{e^{ - 3{\rm \rho}{^{\prime ^2}}/2R_0^2}} \,{e^{i \left[1 + \left(3{{\rm \omega} _{\rm p}}/4{{\rm \omega} _1}\right) - \cos {\rm \theta} \right]{{\rm \omega} _{\rm T}}z^{\prime}/c}}} \over {r - z^{\prime}\cos {\rm \theta}}}}} {\rm \rho}^{\prime} d {\rm \rho}^{\prime} d{\rm \phi}^{\prime} dz^{\prime}.} $$Hence, the vector potential at larger distance becomes,
$$\eqalign{& {\vec A}(r,{\kern 1pt} t) = \hat x\displaystyle{{{{\rm \mu} _0}{J_0}r_{\rm f}^2 \,{e^{ - i{{\rm \omega} _{\rm T}}(t - r/c)}}} \over {4r}} \cr & \quad \displaystyle{{[{e^{i[1 + \left(3{{\rm \omega} _{\rm p}}/4{{\rm \omega} _1}\right) - \cos {\rm \theta} ]{{\rm \omega} _{\rm T}}L/c}} - 1]} \over {i{{\rm \omega} _{\rm T}}[1 + \left(3{{\rm \omega} _{\rm p}}/4{{\rm \omega} _1}\right) - \cos {\rm \theta} ]/c}}.} $$
The term 3ωp/4ω1 inside the parenthesis in Eq. (19) can be neglected for filaments of length 
$L \ll \left(2{{\rm \omega} _1}/3{{\rm \omega} _{\rm p}}\right){{\rm \lambda} _{{\rm THz}}}/{\rm \pi} $, where λTHz is the wavelength of THz radiation. For typical parameters, ω1/ωp~ 100, λTHz~ 100 μm, the filament length .
Therefore, for far field, the magnetic and electric fields of the THz wave are
$$\eqalign{& {\vec B} = \nabla \times {\vec A}{\rm \simeq} \left(i{{\rm \omega} _{\rm T}}/c\right)\hat r \times {\vec A} = \left(\hat r \times \hat x\right) \cr & \quad \displaystyle{{{{\rm \mu} _0}r_{\rm f}^2 {J_0}\,{e^{ - i{{\rm \omega} _{\rm T}}\left(t - r/c\right)}}} \over {4r}}\displaystyle{{\left[{e^{i\left(1 - \cos {\rm \theta} \right){{\rm \omega} _{\rm T}}L/c}} - 1\right]} \over {\left(1 - \cos {\rm \theta} \right)}}, \cr & {\vec E} = - \partial {\vec A}/\partial t = - i{{\rm \omega} _{\rm T}}{\vec A} = \hat x \cr & \quad \displaystyle{{{{\rm \mu} _0}cr_{\rm f}^2 {J_0}\,{e^{ - i{{\rm \omega} _{\rm T}}\left(t - r/c\right)}}} \over {4r}}\displaystyle{{\left[{e^{i\left(1 - \cos {\rm \theta} \right){{\rm \omega} _{\rm T}}L/c}} - 1\right]} \over {\left(1 - \cos {\rm \theta} \right)}}.} $$Hence, the time-averaged Poynting's vector
$$\eqalign{& {{\vec S}_{{\rm av}}} = \hat r\displaystyle{c \over {2{{\rm \mu} _0}}}\left\vert B \right\vert{^2}{\rm \simeq} \hat r\displaystyle{{{{\rm \mu} _0}cr_{\rm f}^4 \left\vert {J_0} \right\vert{^2}} \over {8{r^2}}} \cr & \quad \displaystyle{{{{\sin} ^2} \left[\left(1 - \cos {\rm \theta} \right){{\rm \omega} _{\rm T}}L/2c \right]} \over {{{\left(1 - \cos {\rm \theta} \right)}^2}}}\left(1 - {\sin ^2}{\rm \theta} {\cos ^2}{\rm \phi} \right).} $$
The above equation represents the angular distribution of the radiated THz energy. One may note that as θ decreases, the THz power increases and attains the maximum around θ = 0. For 
${\rm \phi} = {\rm \pi} /2$, θ ~ 0 the maximum power of the radiated field in the forward direction turns out to be
$$\displaystyle{{{{\vec S}_{{\rm av}}}{r^2}} \over {{P_1}}} = \hat r{S_0}{\left( {\displaystyle{{{{\rm \omega} _{\rm T}}L} \over {2c}}} \right)^2}.$$
Normalizing the THz power by peak power of laser, 
${P_1} = {\rm \pi} R_0^2 /2{{\rm \mu} _0}c \vert {A_{10}}{\vert ^2}$, Eq. (21) becomes
$$\displaystyle{{{{\vec S}_{{\rm av}}}{r^2}} \over {{P_1}}} = \hat r{S_0}\displaystyle{{{{\sin} ^2}\left[(1 - \cos {\rm \theta}){{\rm \omega} _{\rm T}}L/2c \right]} \over {{{\left(1 - \cos {\rm \theta} \right)}^2}}}\left(1 - {\sin ^2}{\rm \theta} {\cos ^2}{\rm \phi}\right),$$
where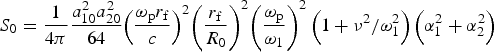 
${S_0} = \displaystyle{1 \over {4{\rm \pi}}} \displaystyle{{a_{10}^2 a_{20}^2} \over {64}}{\left( {\displaystyle{{{{\rm \omega} _{\rm p}}{r_{\rm f}}} \over c}} \right)^2}{\left( {\displaystyle{{{r_{\rm f}}} \over {{R_0}}}} \right)^2}{\left( {\displaystyle{{{{\rm \omega} _{\rm p}}} \over {{{\rm \omega} _1}}}} \right)^2} \left(1 + {{\rm \nu} ^2}/{\rm \omega} _1^2 \right)\left({\rm \alpha} _1^2 + {\rm \alpha} _2^2 \right)$.
Hence, the normalized total THz power can be written as,
$$\displaystyle{{{P_{{\rm THz}}}} \over {{P_1}}} = \int_0^{2{\rm \pi}} {\int_0^{\rm \pi} {\left({{\vec S}_{{\rm av}}}{r^2}/{P_1}\right)}} \sin {\rm \theta} \,d{\rm \theta} \,d{\rm \phi}. $$4. PIC SIMULATION AND DISCUSSION
OSIRIS code (Fonseca et al., Reference Fonseca, Silva, Tsung, Decyk, Lu, Ren, Mori, Deng, Lee, Katsouleas and Adam2002) has been used to carry out the 2D-PIC simulation to trace the THz field inside and outside the plasma filament of finite length and radius. The length (L) and radius (r f) of the plasma column used for the simulation is 1 mm × 16 μm. We here consider a fully ionized plasma column of density n 0 = 1017 cm−3. Corresponding plasma frequency is ωp = 1.77 × 1013 rad/s. The lasers are linearly polarized (
$\hat x$) and propagate in the +z direction. The frequencies of the lasers are taken as ω1 = 2.355 × 1015 rad/s and ω2 = 4.722 × 1015 rad/s, such that the difference frequency 
${{\rm \omega} _{\rm T}} = \left({{\rm \omega} _2} - 2{{\rm \omega} _1}\right) = 1.2{\kern 1pt} \, \times \,{10^{13}}{\rm rad}/{\rm s,}$ lies in the THz range. Corresponding laser wavelengths are λ1 = 800 nm, λ2 = 399 nm, and the peak intensities I 1 = I 2 = 2 × 1014 W cm−2, with the normalized field amplitudes a 10 = 0.01 and a 20 = 0.005. The pulse has a Gaussian temporal shape with T = 150t 0 and the spot sizes r 0 = 6.4 μm, where t 0 = 2π/ω1 is the laser period. The cell size is 0.025 × 0.1 μm2, and the time step interval is 0.03 fs. The total simulation time is 900t 0. In the PIC simulation, the collisional effect has been neglected. Our result only show the short-term and near-field distribution of the THz radiation.
We have traced the electric field of THz radiation close to the laser axis and at distances larger than the filament spot size (r f = 6.4 μm). Fixing z at z = 400λ1 we recorded the THz field in the +x direction. The electric field spectrum of THz wave inside and outside of the plasma filament is plotted in Figure 2. The solid lines represent the THz field inside the filament and the broken lines represent the field outside. The THz spectrum inside and outside the plasma filament are different but carries quite interesting details. Inside the plasma filament, one can see two prominent maximas, corresponding to 
${\rm \omega} /{{\rm \omega} _1} = 0.0037 = {{\rm \omega} _{\rm p}}/2{{\rm \omega} _1},$ that is, ω = ωp/2 and 
${\rm \omega} /{{\rm \omega} _1} = 0.0075 = {{\rm \omega} _{\rm p}}/\Delta {\rm \omega}, $ that is, ω = ωp. The minima between these frequencies is at 
${\rm \omega} /{{\rm \omega} _1} = 0.005 = {{\rm \omega} _{\rm T}}/{{\rm \omega} _1},$ that is, ω = ωT, corresponding f = ωT/2π = 2 THz. This is because the lasers exert ponderomotive force on electrons at frequency 2ω1 and at beat frequency Δω. The ponderomotive force together with the self-consistent field, gives rise to density perturbations at 2ω1 and Δω [cf. the denominator part of Eqs. (11) and (12)]. These density perturbations drive a nonlinear current at ωT = ω2− 2ω1 [cf. Eq. (13)] and generate the p-polarized electromagnetic wave radiation. Thus, the two maximas appearing in the spectrum are because of the two terms in nonlinear current J x. As one moves out of the filament, the aforementioned maximas decrease and disappear at x = 2.5r f, as shown in Figure 2, giving rise to a single maxima around ω = 0.005ω1 = ωT. One may also note that the field amplitude decreases steadily with increase in distance x within the filament, and outside, the amplitude decreases rapidly with distance and the spectrum broadens as well.
Fig. 2. The electric field spectrum of THz wave inside and outside of the plasma filament. The solid lines represent the THz field inside the filament and the broken lines represent the field outside.
From Eq. (20), we obtain the angular distribution of the far-field THz wave. As the angle θ ~ 0, one gets from Eq. (20) the on-axis THz field strength, 
$E = \left({n_0}er_{\rm f}^2 /16{{\rm \varepsilon} _0}r\right) \left({{\rm \omega} _{\rm T}}L/2c\right){a_{20}}a_{10}^2 $. The electric field of the THz is proportional to plasma density n 0, square of filament radius r f, the filament length L, and inverse of distance r. To validate the efficacy of our analytical calculation, we compare the profile of THz field [From Eq. (20)] with the experimental results of Zhong et al. (Reference Zhong, Karpowicz and Zhang2006). Zhong et al. (Reference Zhong, Karpowicz and Zhang2006) have investigated the THz radiation emission via four-wave mixing in air plasma and have observed highly directional THz waves with a divergence angle smaller than 10°. For our analytical calculation, we used plasma density n 0 = 1017 cm−3. Figure 3 shows the angular distribution of THz field at a distance r = 1 m, plotted for the filament lengths L = 3.9 mm (black), 8.9 mm (blue), 13 mm (red), and 35 mm (green). We have used the same filament lengths obtained by Zhong et al. (Reference Zhong, Karpowicz and Zhang2006). One may note that the THz field amplitude attains maximum at θ = 0 and falls rapidly with increasing angle. This means that the radiation emission is largely contained in the forward direction. With an eightfold increase in the filament length, the THz field profile gets strongly modified and becomes highly directional with a divergence angle less than 10°. Hence, it clearly indicates that our analytical result in Figure 3 is comparable with the experimental results of Zhong et al. (Reference Zhong, Karpowicz and Zhang2006).
Fig. 3. Variation of normalized THz field |E|2 (arb. units) with angle θ for the filament lengths L = 3.9 mm (black), 8.9 mm(blue), 13 mm (red), and 35 mm (green).
We would now compare the angular distribution of the THz yield with the experimental results of Gorodetsky et al. (Reference Gorodetsky, Koulouklidis, Massaouti and Tzortzakis2014). Gorodetsky et al. (Reference Gorodetsky, Koulouklidis, Massaouti and Tzortzakis2014) have proposed a model to explain the conical behavior of the THz emission from the two-color laser-induced plasma filaments. Their studies show that for a nonuniform plasma filament the conical angle remains constant with the filament length, while the angle decreases with length for uniform plasma. In our case, we have considered a uniform plasma filament as mentioned before. Figure 4 shows the angular distribution of the normalized THz yield for the filament lengths L = 2.8 mm (black), 10.5 mm (blue), and 17.7 mm (red). Here we used the filament lengths of Gorodetsky et al. (Reference Gorodetsky, Koulouklidis, Massaouti and Tzortzakis2014) for the comparative study. The THz power is null along the laser axis (θ = 0) and attains maxima between the angles 
${\rm \theta} = 2\mathop {\sin} \nolimits^{ - 1} \left(\sqrt {N/L{{\rm \omega} _{\rm T}}/c} \right)$, where N = π, 2π, 3π,…,nπ. Therefore larger the filament length L, smaller will be the emission cone angle. Figure 5 shows the variation of conical angle with the filament length. The half angular width calculated from the above expression can reproduce the experimental results of Gorodetsky et al. (Reference Gorodetsky, Koulouklidis, Massaouti and Tzortzakis2014). For example, the half angular width of the first strongest maxima (for N = π) for L = 10.5 mm turns out to be θ 1/2 = 5°, which agrees well with the experimental results of Gorodetsky et al. (Reference Gorodetsky, Koulouklidis, Massaouti and Tzortzakis2014).
Fig. 4. Variation of normalized THz yield (arb. units) with angle θ for the filament lengths L = 2.8 mm (black), 10.5 mm (blue), and 17.7 mm (red).
Fig. 5. Variation of conical angle with filament length.
Finally, we compare analytically calculated yield (P THz/P 1) with the experimental results obtained by Oh et al. (Reference Oh, You, Jhajj, Rosenthal, Milchberg and Kim2013). Oh et al. (Reference Oh, You, Jhajj, Rosenthal, Milchberg and Kim2013) have studied high-power THz radiation generation via two-color laser filamentation and have achieved filament lengths varying from few centimeters to 1.5 m by increasing the input laser energy. Hence for a filament of length L = 1 m, the half angular width of the first strongest emission cone turns out to be 0.5° and corresponding yield P THz/P 1 = 1.6 × 10−5, which is comparable with the estimation of Oh et al. (Reference Oh, You, Jhajj, Rosenthal, Milchberg and Kim2013).
5. CONCLUSION
In conclusion, we have studied four-wave mixing process for THz radiation generation when two-color laser pulses propagate in the plasma. The THz field amplitude scales with laser intensity as 
${I_1}\sqrt {{I_2}} $ and proportional to plasma density n 0. The polarization of the lasers are kept same to enhance the emission of THz radiation. The lasers drive a nonlinear current at ω and generate the p-polarized electromagnetic wave radiation. Using 2D-PIC simulations we analyzed the spectrum of THz field both inside and outside the plasma filament. Inside the filament the spectrum showed two prominent maximas at ωp/2ω1 and ωp/Δω supporting our analytical framework. These maximas merge together to form a single maxima around ωT/2π = 2 THz outside the filament. The field amplitude decreases steadily with increase in distance x within the filament, and outside, the amplitude decreases rapidly with distance and the spectrum broadens as well.
From the angular distribution of the THz field profile, the radiation emission is found to be largely contained in the forward direction. The THz power and amplitude are found to be very sensitive to the filament length. Hence, the THz power can be increased by increasing the filament length, also by using more laser power. The analytically calculated THz field amplitude and yield are found to be in agreement with the previous studies. The THz radiation intensities from such mechanism is far lower than the photon ionization current mechanism where ionization current dominates radiation. However, this mechanism does not depend on ionization current which usually results from residual ionization momentum, the radiation current here is excited by the ponderomotive force of the two-color beat wave. For an existed fully ionized gas plasma, the former photon ionization current generation mechanism does not work, the current model still works. However, the radiated THz field should be smaller with several orders of magnitude. At the same time, in our model, some basic THz radiation characters are the same as other models, such as the radiation intensity dependence on the two-color intensities and angular distributions. To get a correct explanation of THz generation mechanism in an experiment, careful studies should be made by comparing more aspects of radiation characters.
ACKNOWLEDGEMENTS
This work was supported by the National Basic Research Program of China (Grant Nos. 2013CBA01504, and 2014CB339801), and the National Science Foundation of China (Grant Nos. 11421064, 11374209, and 11374210). M.C. appreciates supports from Shanghai Science and Technology Commission (Grant No. 13PJ1403600). Simulations were performed on the Supercomputer PI at Shanghai Jiao Tong University. The authors would like to acknowledge the OSIRIS Consortium, consisting of UCLA and IST (Lisbon, Portugal) for the use of OSIRIS. M.K. appreciates the useful discussions with Feiyu Li.
