2. SELF-FOCUSING OF AMPLITUDE-MODULATED LASER BEAM

Consider, a high-power amplitude-modulated Gaussian laser beam propagating along the x-direction with frequency ω₀ and wave vector $\overrightarrow {k_0} $ in the magnetoplasma, having static magnetic field (B ₀), perpendicular to the direction of propagation (z-direction) of the beam. The electric field of the laser beam for the extraordinary mode (x-mode) is given by

(1)$$\eqalign{\vec E\left( { = \hat xE_x + \hat yE_y} \right) & = \left\{ {\hat xA_x (x,y,z,t) + \hat yA_y (x,y,z,t)} \right\}\cr & \,\,\quad \times \exp \left\{ { - i\left( {{\bf k}_0 x - {\rm \omega} _0 t} \right)} \right\}}$$

where $E_x = - \left( {{\raise0.7ex\hbox{${{\rm \varepsilon} _{xy}} $} \!\mathord{\left/ {\vphantom {{{\rm \varepsilon} _{xy}} {{\rm \varepsilon} _{xx}}}} \right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\rm \varepsilon} _{xx}} $}}} \right)E_y $, ${\rm \varepsilon} _{xx} = 1 - {\rm \omega} _{\rm p}^2 /( {{\rm \omega} _0^2 - {\rm \omega} _{\rm p}^2} ),$ and ${\rm \varepsilon} _{xy} = {\rm \omega} _{\rm c} {\rm \omega} _{\rm p}^2 /i{\rm \omega}_0({\rm \omega} _0^2 - {\rm \omega} _{\rm p}^2 )$. Due to the nonuniform spatial profile of the amplitude-modulated Gaussian beam, the maximum irradiance occur at the center and decreases in the radial direction. When the laser beam is propagating in magnetized plasma, then density redistribution occurs along the magnetic field due to the ponderomotive force (Sharma, Reference Sharma1978). The ponderomotive force along the external applied magnetic field can be written as (Sharma, Reference Sharma1978; Sodha et al., Reference Sodha, Singh and Sharma1979),

(2)$$\eqalign{F_{{\rm p}z} & = \displaystyle{{ - e^2} \over {4m_{\rm e} ({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}\displaystyle{\partial \over {\partial z}}\cr & \quad \times \left\{ {\left( {E_x. E_x^ \ast + E_y. E_y^ \ast} \right) + \displaystyle{{i{\rm \omega} _{\rm c}} \over {{\rm \omega} _0}} \left( {E_y. E_x^ \ast - E_x. E_y^ \ast} \right)} \right\}}$$

where ω_c = eB ₀/m _ec is the electron cyclotron frequency. The modified density of electrons can be written as follows (Sodha et al., Reference Sodha, Ghatak and Tripathi1974a, Reference Sodha, Sharma and Tripathib, Reference Sodha, Singh and Sharma1979, Reference Sodha, Salimullah and Sharma1980):

(3)$$n = n_0 \exp \left( { - {\rm \alpha} E_y. E_y^\ast} \right)$$

where

$${\rm \alpha} = \displaystyle{{e^2} \over {8k_{\rm B} T_0 m_{\rm e} ({\rm \omega} _0^2 - {\rm \omega} _{\rm c}^2 )}}\left[ {1 + \displaystyle{{{\rm \omega} _{\rm c}^2 {\rm \omega} _{\rm p}^4} \over {{\rm \omega} _0^2 ({\rm \omega} _0^2 - {\rm \omega} _{\rm h}^2 )^2}} +\displaystyle{{2{\rm \omega} _{\rm c}^2 {\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0^2 ({\rm \omega} _0^2 - {\rm \omega} _{\rm h}^2 )}}} \right],$$

${\rm \omega} _{\rm h} = ( {{\rm \omega} _{\rm p}^2 + {\rm \omega} _{\rm c}^2} )^{1/2} $, k _B is the Boltzmann constant and T ₀ is the electron temperature. The wave equation can be written as,

(4)$$\nabla ^2 \vec E - \nabla \left( {\nabla. \vec E} \right) = \displaystyle{{4{\rm \pi}} \over {c^2}} \displaystyle{{\partial \vec J} \over {\partial t}} + \displaystyle{1 \over {c^2}} \displaystyle{{\partial ^2 \vec E} \over {\partial t^2}} $$

where $\vec J = - ne\left( {v_x \hat x + v_y \hat y} \right)$. Now using Eq. (1) in Eq. (4) and separating the x and y components of the wave equation, we obtain as follows:

(5a)$$A_x = \displaystyle{{i{\rm \omega} _{\rm c}} \over {{\rm \omega} _0}} \displaystyle{{{\rm \omega} _{\rm p}^2} \over {({\rm \omega} _0^2 - {\rm \omega} _{\rm h}^2 )}}A_y$$

(5b)$$\eqalign{ &- 2i{\bf k}_0 \displaystyle{{\partial A_y} \over {\partial x}} + {\rm \delta} _ + \displaystyle{{\partial ^2 A_y} \over {\partial y^2}} + \displaystyle{{\partial ^2 A_y} \over {\partial z^2}} \cr & \quad = \left( {\displaystyle{{n - n_0} \over {n_0}}} \right) \times \displaystyle{{{\rm \omega} _{\rm p}^2} \over {c^2}} \displaystyle{{\left( {{\rm \omega} _0^2 - {\rm \omega} _{\rm p}^2} \right)} \over {\left( {{\rm \omega} _0^2 - {\rm \omega} _{\rm h}^2} \right)}}A_y + \displaystyle{{2i{\rm \omega} _0} \over {c^2}} \displaystyle{{\partial A_y} \over {\partial t}}}$$

where ${\rm \delta} _ + = 1 \!-\! {\rm \omega} _{\rm c}^2 {\rm \omega} _{\rm p}^4 /{\rm \omega} _0^2 ({\rm \omega} _0^2 \!-\! {\rm \omega} _{\rm h}^2 )^2 $ and ${\bf k}_0 = ({\rm \omega} _0 /c)\{ 1 - $$({\rm \omega} _{\rm p}^2 ({\rm \omega} _0^2 - {\rm \omega} _{\rm p}^2 )/{\rm \omega} _0^2 ({\rm \omega} _0^2- {\rm \omega} _{\rm h}^2 ))\} ^{1/2} $. For the slowly converging and diverging nature of the laser beam, we assume the solution of Eq. (5b) as follows:

(6)$$A_y \left( {x,y,z,t} \right) = A_0 \left( {x,y,z,t} \right)\exp \left\{ { - i{\bf k}_0 S\left( {x,y,z,t} \right)} \right\}$$

On transforming the coordinates (x, t) to x(=x), ξ = t − x/v _g (where 1/v _g = ω₀/k₀c ²) and by substituting Eq. (6) into (5b), we obtain the real and imaginary parts as follows (Sodha et al., Reference Sodha, Salimullah and Sharma1980):

(7a)$$\displaystyle{{\partial A_0^2} \over {\partial x^2}} + {\rm \delta} _ + A_0^2 \,\displaystyle{{\partial ^2 S} \over {\partial y^2}} + A_0^2 \displaystyle{{\partial ^2 S} \over {\partial z^2}} + {\rm \delta} _ + \displaystyle{{\partial S} \over {\partial y}}\,\displaystyle{{\partial A_0} \over {\partial y}} + \displaystyle{{\partial S} \over {\partial z}}\,\displaystyle{{\partial A_0} \over {\partial z}} = 0$$

(7b)$$\eqalign{2\displaystyle{{\partial S} \over {\partial x}} + {\rm \delta} _ + \left( {\displaystyle{{\partial S} \over {\partial y}}} \right)^2 + \,\left( {\displaystyle{{\partial S} \over {\partial z}}} \right)^2 & = \displaystyle{1 \over {k_0^2 A_0}} \left( {{\rm \delta} _ + \displaystyle{{\partial ^2 A_0} \over {\partial y^2}} + \displaystyle{{\partial ^2 A_0} \over {\partial z^2}}} \right) \cr & \quad - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {k_0^2 c^2}} \displaystyle{{({\rm \omega} _0^2 - {\rm \omega} _{\rm p}^2 )} \over {({\rm \omega} _0^2 - {\rm \omega} _{\rm h}^2 )}}\left( {\displaystyle{{n - n_0} \over {n_0}}} \right)}$$

The solution of Eqs (7a) and (7b) can be written as,

(8a)$$A_0^2 = \displaystyle{{E_{00}^2 (1 + {\rm \mu} \cos \Omega {\rm \xi} )^2} \over {\,f_1 f_2}} \exp \left( { - \displaystyle{{y^2} \over {r_0^2 \,f_1^2}} - \displaystyle{{z^2} \over {r_0^2 \,f_2^2}}} \right)$$

and

(8b)$$S = \displaystyle{{y^2} \over 2}{\rm \beta} _1 (x) + \displaystyle{{z^2} \over 2}{\rm \beta} _2 (x)$$

The intensity variation of the laser beam is described by Eq. (8a), which depends on the dimensionless beam width parameters f ₁ and f ₂ along the propagation direction, in the paraxial regime. Now, putting Eqs (8a) and (8b) in Eq (7a) and comparing the coefficients of y ² and z ², we can get the value of β₁(x) = (1/δ₊)(df ₁/dx) and β₂(x) = df ₂/dx. The governing equations for dimensionless beam width parameters f ₁ and f ₂ can be obtained from Eq. (7b) as follows (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968):

(9a)$$\eqalign{\displaystyle{{d^2 f_1} \over {dx^2}} & = \displaystyle{{{\rm \delta} _ + ^2} \over {k_0^2 r_0^4 \,f_1^3}} - \displaystyle{{{\rm \delta} _ + {\rm \omega} _{\rm p}^2} \over {k_0^2 c^2}} \displaystyle{{({\rm \omega} _0^2 - {\rm \omega} _{\rm p}^2 )} \over {({\rm \omega} _0^2 - {\rm \omega} _{\rm h}^2 )}}\displaystyle{{\,{\rm \alpha} E_{00}^2 \,(1 + {\rm \mu} \cos \Omega {\rm \xi} )^2} \over {r_0^2 \,f_1^2 f_2}} \cr & \quad \times \exp \left( { - \displaystyle{{{\rm \alpha} E_{00}^2 (1 + {\rm \mu} \cos \Omega {\rm \xi} )^2} \over {\,f_1\, f_2}}} \right)}$$

(9b)$$\eqalign{\displaystyle{{d^2 f_2} \over {dx^2}} & = \displaystyle{1 \over {k_0^2 r_0^4 \,f_2^3}} - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {k_0^2 c^2}} \displaystyle{{({\rm \omega} _0^2 - {\rm \omega} _{\rm p}^2 )} \over {({\rm \omega} _0^2 - {\rm \omega} _{\rm h}^2 )}}\displaystyle{{\,{\rm \alpha} E_{00}^2 \,(1 + {\rm \mu} \cos {\rm \Omega \xi} )^2} \over {r_0^2 \,f_1 \,f_2^2}} \cr & \quad \times \exp \left( { - \displaystyle{{{\rm \alpha} E_{00}^2 \left( {1 + {\rm \mu} \cos {\rm \Omega \xi}} \right)^2} \over {\,f_1 \,f_2}}} \right)}$$

Equations (9a) and (9b) show the variation of dimensionless beam width parameter in the magnetoplasma.

3. THZ RADIATION

For the generation of THz radiation, we consider the propagation of amplitude-modulated Gaussian laser beam, with electric field as given by Eq. (1), through the ripple density plasma with density variations given as: n = n ₀ + n _qe ^−iqx , where n _q and q are amplitude and wave number of the density ripple, respectively. The electrons also respond at the modulated frequency of pump laser on account of ponderomotive force. This oscillatory velocity couples with the density ripple and leads to the generation of nonlinear current density, which is the source of THz radiation. The density ripple in the plasma is playing the key role for the propagation of generated THz wave. The ponderomotive force at modulated frequency (Ω ≪ ω₀) can be written as,

(10)$$\eqalign{\vec F_{\rm P}^\Omega \left( { = - \displaystyle{{e^2} \over {2m_{\rm e} {\rm \omega} _0^2}} \overrightarrow \nabla \left. {\left( {\vec E.\vec E^ \ast} \right)} \right \vert _\Omega} \right) & = \left( {\hat xF_{{\rm p}x0} + \hat yF_{{\rm p}y0} + \hat zF_{{\rm p}z0}} \right)\cr & \quad \; \times \exp \left\{ {i\Omega \left( {t - \displaystyle{x \over {v_{\rm g}}}} \right)} \right\}}$$

The nonlinear oscillatory velocity of the electrons at modulated frequency Ω(=ω_T) can be obtained from the equation of motion as follows:

(11)$$\displaystyle{{\partial \vec v_{{\rm nl}}} \over {\partial t}} = - \left( {\vec v_{{\rm nl}} \times \hat z} \right){\rm \omega} _{\rm c} + \displaystyle{{\vec F_{\rm P}^\Omega} \over {m_{\rm e}}} $$

The nonlinear oscillatory velocity components can be evaluated from Eq. (11) as (Ginzburg, Reference Ginzburg1970), $v_x^{{\rm nl}} = ({\rm \omega} _{\rm T} F_{{\rm p}x}^{\rm \Omega} + i{\rm \omega} _{\rm c} $$ F_{{\rm p}y}^{\rm \Omega} )/im_{\rm e} ({\rm \omega} _{\rm T}^2 - {\rm \omega} _{\rm c}^2 )$ and $v_y^{{\rm nl}} = ({\rm \omega} _{\rm T} F_{{\rm p}y}^{\rm \Omega} - i{\rm \omega} _{\rm c} F_{{\rm p}x}^{\rm \Omega}) /im_{\rm e} ({\rm \omega} _{\rm T}^2 - {\rm \omega} _{\rm c}^2 ).$The wave equation for THz generation in magnetized plasma can be written as,

(12)$$\nabla ^2 \vec E_{\rm T} - \nabla \left( {\nabla. \vec E_{\rm T}} \right) = \displaystyle{{4{\rm \pi}} \over {c^2}} \displaystyle{{\partial (\vec J_{\rm T}^{\;\rm l} + \vec J^{{\rm nl}} )} \over {\partial t}} + \displaystyle{1 \over {c^2}} \displaystyle{{\partial ^2 \vec E_{\rm T}} \over {\partial t^2}} $$

Now considering the THz radiation in the extra ordinary mode (E _Tz = 0, E _Tx ≠ 0, E _Ty ≠ 0). The linear oscillatory velocity of the electrons at THz frequency (ω_T) and wave number (k _T) can be written as (Ginzburg, Reference Ginzburg1970) $v_{{\rm T}x}^{\rm l} = ie$$({\rm \omega} _{\rm T} E_{{\rm T}x} + i{\rm \omega} _{\rm c} E_{{\rm T}y} )/m_{\rm e} ({\rm \omega} _{\rm T}^2 - {\rm \omega} _{\rm c}^2 )$ and $v_{{\rm T}y}^{\rm l} = ie({\rm \omega} _{\rm T} E_{{\rm T}y} \!-\! i{\rm \omega} _{\rm c} E_{{\rm T}x} )$$/m_{\rm e} ({\rm \omega} _{\rm T}^2 - {\rm \omega} _{\rm c}^2 )$. The linear and nonlinear current density at THz wave number and frequency can be written as

$$\vec J_{\rm T}^{\;\rm l} = - en_0 \left( {v_{{\rm T}x}^{\rm l} \hat x + v_{{\rm T}y}^{\rm l} \hat y} \right)$$

and

(13)$$\vec J^{{\,\rm nl}} = \displaystyle{{ - en_q e^{ - iqx}} \over 2} \left( {v_x^{{\rm nl}} \hat x + v_y^{{\rm nl}} \hat y} \right)$$

Now taking the fast phase variation $\vec E_{\rm T} = \vec E_{{\rm T}0} \left( {x,y} \right)\exp \left\{ { - i\left( {k_{\rm T} x - {\rm \omega} _{\rm T} t} \right)} \right\}$, we evaluate the x and y component of Eq. (12) as follows:

(14a)$$E_{{\rm T}x} = \displaystyle{{4{\rm \pi} i} \over {{\rm \omega} _{\rm T}}} \left( {J_{{\rm T}x}^{\rm l} + J_y^{{\rm nl}}} \right)$$

and

(14b)$$\eqalign{&2ik_{\rm T} \displaystyle{{\partial E_{{\rm T}y{\rm 0}}} \over {\partial x}} + \left\{ {k_{\rm T}^2 - \displaystyle{{{\rm \omega} _{\rm T}^2} \over {c^2}} \left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _{\rm T}^2}} \displaystyle{{{\rm \omega} _{\rm T}^2 - {\rm \omega} _{\rm p}^2} \over {{\rm \omega} _{\rm T}^2 - {\rm \omega} _{\rm H}^2}}} \right)} \right\}E_{{\rm T}y0} \cr & \quad = \left( {\displaystyle{{n_q} \over {2n_0}}} \right)\left( {\displaystyle{{{\rm \omega} _{\rm p}^2} \over {c^2}}} \right)\displaystyle{{\{ i{\rm \omega} _{\rm c} {\rm \omega} _{\rm T} F_{{\rm p}x{\rm 0}}^{\rm \Omega} - ({\rm \omega} _{\rm T}^2 - {\rm \omega} _{\rm p}^2 )F_{{\rm p}y{\rm 0}}^{\rm \Omega} \}} \over {({\rm \omega} _{\rm T}^2 - {\rm \omega} _{\rm H}^2 )}}}$$

where 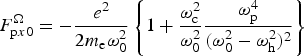$F_{{\rm p}x0}^{\Omega} = - \displaystyle{{e^2} \over {2m_{\rm e} {\rm \omega}_0^2}} \left\{ 1 +\displaystyle{{{\rm \omega}_{\rm c}^2} \over {{\rm \omega}_0^2}} \displaystyle{{{\rm \omega}_{\rm p}^4} \over {({\rm \omega}_0^2 - {\rm \omega}_{\rm h}^2 )^2}} \right\}$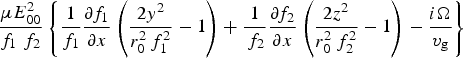$\displaystyle{{{\rm \mu} E_{00}^2} \over {f_1\;f_2}} \left \{ \displaystyle{1 \over {f_1}} \displaystyle{{\partial f_1} \over {\partial x}}\left( \displaystyle{{2y^2} \over {r_0^2\,f_1^2}} - 1 \right) + \displaystyle{1 \over {\,f_2}} \displaystyle{{\partial f_2} \over {\partial x}} \left( \displaystyle{{2z^2} \over {r_0^2 \,f_2^2}} - 1 \right) - \displaystyle{{i\Omega} \over {v_{\rm g}}} \right \} $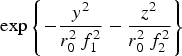$\exp \left\{ - \displaystyle{{y^2} \over {r_0^2 \,f_1^2}} - \displaystyle{{z^2} \over {r_0^2 \,f_2^2}}\right\}$ and 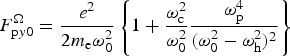$F_{{\rm p}y0}^{\rm \Omega} = \displaystyle{{e^2} \over {2m_{\rm e} {\rm \omega}_0^2}} \left\{ 1 + \displaystyle{{{\rm \omega}_{\rm c}^2} \over {{\rm \omega}_0^2}} \displaystyle{{{\rm \omega}_{\rm p}^4} \over {({\rm \omega}_0^2 - {\rm \omega}_{\rm h}^2 )^2}} \right\}$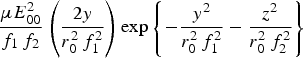$\displaystyle{{{\rm \mu} E_{00}^2} \over {f_1 \,f_2}} \left( \displaystyle{{2y} \over {r_0^2 \,f_1^2}} \right) \exp \left\{ - \displaystyle{{y^2} \over {r_0^2 \,f_1^2}} - \displaystyle{{z^2} \over {r_0^2 \,f_2^2}} \right\}$. The phase matching demands that $k_{\rm T} = ({\rm \omega}_{\rm T}/c) \{1- ({\rm \omega}_{\rm p}^2 ({\rm \omega}_{\rm T}^2 - {\rm \omega}_{\rm p}^2) /{\rm \omega}_{\rm T}^2({\rm \omega}_{\rm T}^2 - {\rm \omega}_{\rm h}^2))\}^{1/2},$while the wave vector satisfies the phase-matching condition k _T = Ω/v _g + q.

4. RESULTS AND DISCUSSION

Equations (9a) and (9b) show the converging/diverging behavior of the laser beam in magnetized plasma. On the right-hand side of both the equations [Eqs (9a) and (9b)], the first term shows divergence (diffraction), while the second term is responsible for the convergence (nonlinear term) of the beam. We have solved the coupled Eqs (9a) and (9b) numerically by Runge–Kutta methods and using the following boundary conditions (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968):$\mathop {\left. {\,f_1} \right\vert}\nolimits_{ x \,=\, 0} = $$\mathop {\left. {\mathop f\nolimits_2} \right\vert}\nolimits_{ x \,=\, 0} = \,1\;{\rm and}\;{\mathop {\left. {d\mathop f\nolimits_1 /dx} \right\vert}\nolimits_{x \,=\, 0} = \mathop {\left. {d\mathop f\nolimits_2 /dx} \right\vert}\nolimits_{ x \,=\, 0} = 0} $. For the numerical illustration, we have chosen the following set of laser (CO₂)–plasma parameters: intensity of the laser beam, 10¹⁴ W/cm², initial radius of the laser beam, r ₀ = 30 µm, ω₀ = 1.78 × 10¹⁴ rad/s, ω_p = 2.5 × 10¹³ rad/s, modulated frequency of laser beam, Ω = 1.5ω_p, μ = 0.1, ω_c = 0.1ω_p, and 0.6ω_p. Figures 1(a) and 1(b) show the variation of dimension less beam width parameters f ₁ and f ₂ with the normalized distance η, where η = x/R _d and $R_{\rm d} ( = {\rm \omega} _0 r_0^2 /c)$ is the diffraction length. The focusing rate of laser beam decreases with increasing the value of Ωξ = 0, π/2, and π. The applied external magnetic field also significantly affects the self-focusing rate.

Fig. 1. Variation of beam dimensionless width parameters with normalized distance.

Figure 2 shows the schematic diagram for the THz radiation in the presence of external applied static magnetic field in the ripple density plasma. The nonlinear current density at THz frequency arises due to the coupling of nonlinear oscillatory velocity of electron at modulation frequency with the density ripple. The propagation of THz radiation is governed by Eq. (14b) and the results are presented in Figures 3 and 4 for the exact phase-matching condition that is, k _T = Ω/v _g + q. The energy transfer from the amplitude-modulated laser to the generated THz waves will be maxima when the exact phase matching is achieved. Here, the value of ripple wave number (q) is the key factor to achieve the exact phase-matching condition and for determining the interaction length. However, the generated THz wave can propagate in the magnetized plasma when the frequency of the generated wave lie either in between the left-hand cut-off frequency $({\rm \omega} _{\rm L} = 1/2[ - {\rm \omega} _{\rm c} + ({\rm \omega} _{\rm c}^2 + 4{\rm \omega} _{\rm p}^2 )^{1/2} ])$ and upper hybrid frequency (ω_h) or greater than the right-hand cut-off frequency $({\rm \omega} _{\rm R} = 1/2[{\rm \omega} _{\rm c} + ({\rm \omega} _{\rm c}^2 + 4{\rm \omega} _{\rm p}^2 )^{1/2} ])$. In the present study, the right-hand cut-off frequency ω_R corresponding to ω_c = 0.1ω_p and 0.6ω_p come out to be 2.73 × 10¹³ and 3.49 × 10¹³ rad/s, respectively, which is smaller than the generated THz radiation frequency ω_T(=3.77 × 10¹³ rad/s). Thus it can be seen that the generated THz wave will propagate through the plasma. Since the maximum energy transfer takes place near the resonance condition (ω_T ≈ ω_h) for the THz radiation, hence the generation of THz radiation can be optimized by the strength of the externally applied magnetic field. The THz field radiation increases with increasing value of static magnetic field as ω_T approaches to the ω_h, and the wave is resonantly excited. The generated THz wave amplitude yield decreases with increasing value of Ωξ, because the focusing of laser beam decreases with increasing value of Ωξ. However, the laser power will decrease with the distance of propagation on account of the absorption (due to collisions) of the laser beam. Hence, the yield of the generated THz radiation will also fall with the distance of propagation due to absorption. This constraint has been taken care of by considering collisionless plasma (i.e., $\nu _0 /{\rm \omega} _0 \sim 10^{ - 4} $, where v ₀ is the collisional frequency) as well as the THz absorption length to be larger than interaction length in the numerical calculations. In Figures 3(a) and 3(b), dotted black lines show the generation of THz radiation in the case of laser beam propagation without divergence or convergence that is, f ₁(x) = f ₂(x) = 1while solid lines show for the case of self-focused laser beam. The generated THz radiation field with the radial distance (y/r ₀) has been plotted in Figure 4.

Fig. 2. Schematic diagram for the THz radiation in magnetized ripple density plasma.

Fig. 3. Variation of THz radiation amplitude with normalized distance around the maximum irradiance (y/r ₀ = 0.4, z = 0) for (a) ω_c = 0.1ω_p and (b) ω_c = 0.6ω_p for n _q = 0.2n ₀.

Fig. 4. Variation of THz radiation amplitude with radial distance y/r ₀ of the laser beam for n _q = 0.2n ₀.

The amplitude of the generated THz radiation increases with the distance of propagation. In the case of exact phase-matching condition, one can generate the strong THz radiation due to infinite interaction length. But the power of the laser beam can be reduced with the distance of propagation due to diffraction and collision (or any nonlinear mechanism) in the plasma and the less power are available for the generation of THz radiation, even when/when the exact phase-matching condition is satisfied. The self-focused laser beam is able to propagate longer distances in the plasma and as a result the energy conversion from laser to THz radiation is enhanced, as compared with that without self-focusing of the laser beam. Figures 5(a) and 5(b) show the power spectrum for the generation of THz radiation around the maximum irradiance (y/r ₀ = 0.4, z = 0) with and without self-focusing (i.e., f ₁(x) = f ₂(x) = 1) for n _q = 0.2n ₀, ω_c = 0.1ω_p, and 0.6ω_p, respectively.

Fig. 5. Power spectra of THz radiation with cross-focusing (solid line) and without cross-focusing (dotted line) of laser beams at y/r ₁ = 0.4 for (a) ω_c = 0.1ω_p and (b) ω_c = 0.6ω_p for n _q = 0.2n ₀.