Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-11T17:37:10.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Target heating in high-energy-density matter experiments at the proposed GSI FAIR facility: Non-linear bunch rotation in SIS100 and optimization of spot size and pulse length

Published online by Cambridge University Press:  01 October 2004

N.A. TAHIR ,
S. UDREA ,
C. DEUTSCH ,
V.E. FORTOV ,
N. GRANDJOUAN ,
V. GRYAZNOV ,
D.H.H. HOFFMANN ,
P. HÜLSMANN ,
M. KIRK  and
I.V. LOMONOSOV
...Show all authors
N.A. TAHIR
Affiliation:
Gesellschaft für Schwerionenforschung, Darmstadt, Germany
S. UDREA
Affiliation:
Institut für Kernphysik, Technische Universität Darmstadt, Germany
C. DEUTSCH
Affiliation:
Laboratoire de Physik des Gaz et des Plasmas, Universite Paris-Sud, Orsay, France
V.E. FORTOV
Affiliation:
Institute of Problems of Chemical Physics, Russian Academy of Sciences, Chernogolovka, Russia
N. GRANDJOUAN
Affiliation:
Ecole Polytechnique, CNRS-CEA, Universite Paris VI, Palaiseau, France
V. GRYAZNOV
Affiliation:
Institute of Problems of Chemical Physics, Russian Academy of Sciences, Chernogolovka, Russia
D.H.H. HOFFMANN
Affiliation:
Gesellschaft für Schwerionenforschung, Darmstadt, Germany Institut für Kernphysik, Technische Universität Darmstadt, Germany
P. HÜLSMANN
Affiliation:
Gesellschaft für Schwerionenforschung, Darmstadt, Germany
M. KIRK
Affiliation:
Gesellschaft für Schwerionenforschung, Darmstadt, Germany
I.V. LOMONOSOV
Affiliation:
Institute of Problems of Chemical Physics, Russian Academy of Sciences, Chernogolovka, Russia
A.R. PIRIZ
Affiliation:
E.T.S.I. Industriales, Universidad de Castilla-La Mancha, Ciudad Real, Spain
A. SHUTOV
Affiliation:
Institute of Problems of Chemical Physics, Russian Academy of Sciences, Chernogolovka, Russia
P. SPILLER
Affiliation:
Gesellschaft für Schwerionenforschung, Darmstadt, Germany
M. TEMPORAL
Affiliation:
E.T.S.I. Industriales, Universidad de Castilla-La Mancha, Ciudad Real, Spain
D. VARENTSOV
Affiliation:
Institut für Kernphysik, Technische Universität Darmstadt, Germany
Rights & Permissions [Opens in a new window]

Abstract

The Gesellschaft für Schwerionenforschung (GSI) Darmstadt has been approved to build a new powerful facility named FAIR (Facility for Antiprotons and Ion Research) which involves the construction of a new synchrotron ring SIS100. In this paper, we will report on the results of a parameter study that has been carried out to estimate the minimum pulse lengths and the maximum peak powers achievable, using bunch rotation RF gymnastic-including nonlinearities of the RF gap voltage in SIS100, using a longitudinal dynamics particle in cell (PIC) code, ESME. These calculations have shown that a pulse length of the order of 20 ns may be possible when no prebunching is performed while the pulse length gradually increases with the prebunching voltage. Three different cases, including 0.4 GeV/u, 1 GeV/u, and 2.7 GeV/u are considered for the particle energy. The worst case is for the kinetic energy of 0.4 GeV/u which leads to a pulse length of about 100 ns for a prebunching voltage of 100 kV (RF amplitude). The peak power was found to have a maximum, however, at 0.5–1.5kV prebunching voltage, depending on the mean kinetic energy of the ions. It is expected that the SIS100 will deliver a beam with an intensity of 1–2 × 1012 ions. Availability of such a powerful beam will make it possible to study the properties of high-energy-density (HED) matter in a parameter range that is very difficult to access by other means. These studies involve irradiation of high density targets by the ion beam for which optimization of the target heating is the key problem. The temperature to which a target can be heated depends on the power that is deposited in the material by the projectile ions. The optimization of the power, however, depends on the interplay of various parameters including beam intensity, beam spot area, and duration of the ion bunch. The purpose of this paper is to determine a set of the above parameters that would lead to an optimized target heating by the future SIS100 beam.

Keywords

Bunch rotationEquation of stateFAIRHigh energy density matter
Type
Research Article
Information
Laser and Particle Beams , Volume 22 , Issue 4 , October 2004 , pp. 485 - 493
Copyright
© 2004 Cambridge University Press

INTRODUCTION

The Gesellschaft für Schwerionenforschung (GSI), in Darmstadt, Germany, is a unique laboratory worldwide in that it has the capability to generate intense heavy ion beams at the 18 Tm heavy ion synchrotron facility, SIS18. Currently this facility can deliver a uranium beam with an intensity of 4 × 109 ions and a particle energy of a few hundred MeV/u. The particles are delivered in a single bunch which is a few hundred ns long. It is expected that when the upgrade of the SIS18 is completed, the beam intensity will be increased to 2.5 × 1011 ions while the pulse length will be reduced to about 50 ns, and the particle energy will be 197 MeV/u (Müller & Spiller, 1996). The full width at half maximum (FWHM) of the transversal Gaussian beam power profile, which for calculational purposes is considered as the effective beam radius, will be 1.0 mm.

GSI is also planning to build a new, much larger, synchrotron ring, SIS100 (100 Tm magnetic rigidity) that will increase the currently available accelerator capabilities tremendously. This new facility has been named FAIR (Facility for Antiprotons and Ion Research). The SIS18 will be used as an injector for the SIS100 and four to eight bunches from the SIS18 will be transferred to the SIS100 consecutively, where the ions will be further accelerated before the beam is finally delivered onto a target. The SIS100 beam will therefore consist of 1-2 × 1012 uranium ions. A wide range of particle energy (400 MeV/u–2.7 GeV/u) will be available.

In order to find the prebunching voltage that would lead to an optimum power and the corresponding minimum bunch length for the SIS100 beam, we have carried out a parameter study using a particle in cell (PIC) code, ESME (MacLachlan, 1990). We have considered three different values for the particle energy, that is 0.4 GeV/u, 1 GeV/u, and 2.7 GeV/u, respectively. This study shows that without any prebunching it is possible to achieve a bunch length in the order of 20 ns. However, the pulse length increases gradually with the prebunching voltage, and in the worst case, one achieves a bunch length of 100 ns for a particle energy of 0.4 GeV, and a prebunching voltage of 100 kV (RF amplitude). Higher values of the particle energy lead to more optimistic (shorter) values of pulse length.

One of the most interesting experiments that can be done using an intense heavy ion beam is the high-energy-density (HED) matter studies. Previous experiments in this field carried out at the GSI (Funk et al., 1998; Stöwe et al., 1998; Varentsov et al., 2003), detailed numerical simulations (Tahir et al., 2000a, 2000b, 2001, 2003a; Hoffmann et al., 2002), and theoretical modeling (Temporal et al., 2003; Piriz et al., 2002a, 2002b), have shown that intense heavy ion beams are a very efficient tool to induce high-energy-density (HED) states in matter, and can therefore be employed to study the thermophysical properties, especially the equation-of-state (EOS) of these exotic states of matter. SIS100 therefore offers a unique possibility to advance our knowledge of the physical properties of the HED matter including strongly coupled plasmas.

The maximum temperature to which a target can be heated depends on the specific power that is deposited by the beam in the target. The specific power deposition, Ps is estimated by

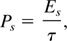
where τ is the pulse duration and Es is the specific energy deposition given by

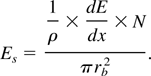
In the above equation, (1/ρ)(dE/dx) is the specific energy loss of a single ion, ρ is the target material density, x is the coordinate along the particle trajectory, N is the total number of particles in the beam and rb is the beam radius.

It is seen from equation (2) that for a given value of the beam intensity, N, the specific energy deposition increases as the inverse square of the beam radius. Therefore, one can increase the Es efficiently by decreasing the beam spot area. However, this cannot be done arbitrarily because there is an implicit interdependence between rb and τ. An increase in Es reduces the hydrodynamic expansion time scale that requires a corresponding reduction in the bunch length in order to have an efficient energy deposition.

We have carried out hydrodynamic simulations to determine the optimum radius focal spot corresponding to the parameters of the SIS100 beam. We have considered three different options for the radius focal spot (full width at half maximum of the Gaussian distribution), that is, 0.5 mm, 1.0 mm, and 1.5 mm, respectively. Our simulations showed that for the pulse length range of 20–100 ns, the value of the beam radius should be 1.0 mm or larger. For the case of 0.5 mm FWHM, the pulse length should be in the order of 5 ns, which at present is not within the design parameters of the SIS100. However, in case the SIS100 operates at a lower intensity, for example, at an N = 1012, one may use a FWHM of 0.5 mm with a pulse length of 20 ns. This combination will compensate for the reduction in the specific energy deposition due to a decrease in the beam intensity. It is therefore important to keep the option of focusing the beam spot to a size with a radius of 0.5 mm as well.

NON-LINEAR BUNCH ROTATION

The RF gymnastic referred to as bunch “rotation” in the most general sense, involves a sudden rise in the RF gap voltage amplitude from an initial value, which may even be zero, to a final value. The distribution of particles when plotted in the longitudinal phase-space (time-energy relative to the synchronous particle) is no longer matched to the constant Hamiltonian contours, this means that the form of the distribution must undergo a rotation as viewed in the longitudinal phase-space. In real space, the bunch length shortens up to a point, then broadens again, and continues in this manner until the incoherence in the phase-space motion of the particles eventually causes the distribution to be completely smeared out resulting in no more bunch rotation. In this study, we are concerned with the extraction of the bunch after it has undergone approximately ¼ of a turn in the phase-space, that is, the first point in time at which the bunch is maximally compressed.

If the beam is small enough compared to the RF bucket area, the area within which the phase-space motion is bound and oscillatory, then the bunch compression equation may be used to calculate the factor reduction in the bunch length as below:

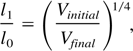
where l0 is the initial and l1 is the final bunch length after the ¼ turn rotation; Vinitial is the initial RF voltage amplitude, and Vfinal is the final amplitude required only if one wishes to maintain the final bunch form without further rotation. In fact, in this study, we immediately fast extract the beam with kicker magnets after the ¼ turn. From the above stated conditions, including low intensity, this rotation frequency may be derived analytically, and is given by:

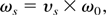
where subscript ωs denotes the synchrotron frequency, νs the tune shift, and ω0 the revolution frequency of the synchronous particle around the circumference of the synchrotron. The tune is given by Chao and Tinger (1998),

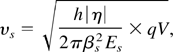
for a stationary bucket. Equations (3)–(5) are valid for bunches that are small compared to the RF bucket, or more specifically, valid for small synchrotron oscillation amplitudes of the particles. The bunch must be centered in the RF bucket to prevent any undesired coherent dipole motion of the bunch. The beam intensity should also be low. In this investigation however, the bunches are generally not small, we may even start from a DC beam, and the intensities are not high.

We thus have to numerically simulate to estimate the pulse length and peak pulse power at the maximum point of bunch compression. This was done with the ESME code (MacLachlan, 1990). The simulation ran for about ½ a synchrotron period, estimated from Equations (4) and (5), and the particle phase-space coordinates were saved approximately every 1 degree of rotation of the core of the beam in the phase-space, in the proximity of the maximum compression point in time, estimated from Equation (4). One could thus estimate to a good degree of accuracy the minimum pulse length and maximum peak power.

Simulations were run for different initial conditions of the beam. Other than the energy of the beam, the so called prebunching RF voltage amplitude Vinitial, which is reached at the point where the bunch rotation procedure begins, was also varied on a per run basis. The machine and beam parameters for the SIS100 simulation are shown in Table 1. The initial phase-space of the beam was an important issue, namely, the choice of the distribution function and its emittance. It was thus decided to start the simulation with a bunched beam in one h = 2nd harmonic RF bucket with a normalized emittance equal to the normalized emittance of the DC beam immediately after the injection process into SIS18 is complete, that is (Δp/p)FWHM = 10−3 at a kinetic energy of 11.4 MeV/u. The intended RF scheme, after the acceleration of the beam is completed, involves an adiabatic debunching of 8 bunches into a barrier bucket, which spans the whole SIS100 circumference. Thereafter, the barrier bucket is slowly reduced to half the initial length, meanwhile the the bucket's momentum acceptance is slowly increased in order to contain all the beam. The beam may then be “prebunched” before the sudden rise to 1 MV on the gap voltage RF amplitude of the compressor cavities running at h = 2. It is at this point in the machine cycle that the initial conditions for the bunch rotation simulation were defined. The whole RF process in SIS100 as well as SIS18, before the bunch rotation itself, must be as quick as possible while keeping the beam emittance growth sufficiently small. This time constraint is set by the relatively short beam life time of U28+ due to the beam induced desorption effect from the beam pipe (Mustafin et al., 2002), which has been observed in SIS18 and is expected in the future GSI synchrotrons.

SIS100 beam and machine parameters

The direct space charge impedance

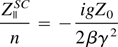
was included during the bunch rotation at the energies concerned (i.e., 0.4 GeV/u, 1 GeV/u, and 2.7 GeV/u). The space charge voltages were small compared to the Vfinal of 1 MV due to the relatively high γ. This can become evident from Equation (6) when considering an intensity of 2 × 1012 ions of 238U28+. The RF voltage amplitude was kept at 1 MV and the phase-space coordinates during the simulation as previously mentioned were saved for further analysis in order to produce Figures 1 and 2. The data analysis was done using the Interactive Data Language (IDL) libraries. Histograms of the line-charge density were derived and consequently the FWHM pulse length as well as the peak power could be evaluated from these histograms, which consisted of 256 bins over the full SIS100 circumference. The peak power was taken as the average power over the bin with the most particles inside it, which lasts for T0 /256 seconds in this case, where T0 is the synchronous revolution frequency.

Minimum pulse length at maximum compression versus Vinitial for 238U28+ at an intensity of 2 × 1012 ions. The energies quoted in the legend are those of the mean kinetic energy per nucleon of the ions. The smooth curves are only for visual guidance.

Peak pulse power versus Vinitial for 238U28+ at an intensity of 2 × 1012 ions. The energies quoted in the legend are those of the mean kinetic energy per nucleon of the ions.

Without any prebunching with the compressor cavities, that is, direct jump to 1 MV, the shortest pulse lengths (FWHM transit times) can be achieved. These shortest times are in the order of 20 ns for 0.4 GeV/u, 1 GeV/u, and 2.7 GeV/u. The dependence is evidently not a strong one. However, there is a maximum in the peak power of the pulse corresponding to a prebunched voltage Vinitial = 1.5 kV. This maximum is supposed to correspond to the initial phase-space of the beam completely filling the RF bucket area at Vinitial. It should be noted that these pulse times may be reduced by reducing the time-window of activation of the fast extraction kicker magnets to below T0, however, at the cost of total intensity delivered to the target.

HYDRODYNAMIC SIMULATION RESULTS

In this section, we present numerical simulations of the hydrodynamic response of a cylindrical target made of solid lead that is irradiated with the SIS100 beam along its length. The beam target geometry is shown in Figure 3. The beam radius is considered to be larger that the target radius and the target length is assumed to be shorter than the range of the projectile ions. These conditions allow for almost uniform energy deposition along the radial as well as the axial direction.

Beam-Target geometry.

We have considered a particle energy of 1.0 GeV/u and according to the SRIM code (Ziegler et al., 1996) the range of these ions in solid lead is about 1.5 cm, so one may use a cylinder with a length of a few mm, and still have uniform deposition along the particle trajectory. The beam intensity is assumed to be 2 × 1012 ions that are delivered in a single bunch which has a parabolic temporal power profile. With the current beam intensities the temperature is not very high, and the cold stopping data provided by the SRIM code is a reasonable approximation. In case of higher temperatures, one should include the temperature dependent effects in the model (Mehlhorn, 1981; Nardi & Zinamon, 1982; Deutsch, 1986). Detailed experimental work has also been done on energy loss measurements of energetic ions in matter (Hoffmann et al., 1990; Bakhmetjev et al., 2003; Hasegawa et al., 2003). The simulations have been carried out using a two-dimensional hydrodynamic code, BIG-2 (Fortov et al., 1996) and a multi-phase EOS model (Bushman & Fortov, 1987) has been used for the lead target.

We consider three different sizes for the beam focal spot, that is, a FWHM of 0.5 mm, 1.0 mm, and 1.5 mm. For these three different cases we use target radii equal to 0.2 mm, 0.4 mm, and 0.6 mm, respectively. Since for all these cases, the target length is much larger than its radius, the expansion along the axial direction is negligible over the time scale of our interest, and the problem therefore reduces to that of a one-dimensional radial expansion.

Spot size with FWHM 0.5 mm

In this case we assume that the target radius is 0.2 mm. First, we consider a pulse length of 50 ns and the results are plotted in Figures 4 and 5. In Figure 4, we present the density vs. the target radius at different times during the irradiation. It is seen that at t = 20 ns the density has significantly been reduced due to substantial expansion of the target material. The target radius at this time has been increased to 0.4 mm from the initial value of 0.2 mm. Therefore, the bulk of the ions that are delivered during the remaining 30 ns of the bunch will pass without losing much of their energy in the target. At t = 30 ns the target radius has become 0.6 mm and the density has been reduced to less than 3 g/cm3. The temperature profiles in Figure 5 show that a maximum temperature in the order of 20 eV is achieved at t = 20 ns, and then during the remaining 30 ns of the pulse, no further heating takes place but instead the temperature decreases due to expansion. This shows that a pulse length of 50 ns is too long for the above beam spot size.

Density vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 0.5 mm, particle energy = 2.7 Gev/u and target radius = 0.2 mm.

Temperature vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 0.5 mm, particle energy = 2.7 Gev/u and target radius = 0.2 mm.

In order to check the minimum pulse length which will be needed for this beam spot size, we carried out simulations using a pulse length of 5 ns. The density and the temperature profiles during the irradiation time are plotted in Figures 6 and 7, respectively. It is seen that the target expansion during the 5 ns pulse is negligible and at the end of the pulse, one achieves a temperature of about 45 eV. In order to have an efficient target heating, it is therefore necessary to have a pulse length of 5 ns with an intensity of 2 × 1012 uranium particles if the beam is focused to a FWHM of 0.5 mm. Although such a short pulse length is at present not within the design parameters of the SIS100, the option of focusing the beam spot size to a FWHM of 0.5 mm should not be excluded for the following reason. If under certain conditions the SIS100 operates at a lower intensity than the maximum design value of 2 × 1012 ions, one can efficiently heat the target using a beam spot size with a FWHM of 0.5 mm and with a pulse length of 20 ns which will compensate for the reduction in the specific energy deposition that would otherwise have resulted due to a loss in beam intensity.

Density vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 5 ns, spot FWHM = 0.5 mm, particle energy = 2.7 Gev/u and target radius = 0.2 mm.

Temperature vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 5 ns, spot FWHM = 0.5 mm, particle energy = 2.7 Gev/u and target radius = 0.2 mm.

Spot size with FWHM 1.0 mm

In this case, we use a target that has a radius of 0.4 mm and the pulse length is assumed to be 50 ns. The density and temperature profiles during the irradiation time are plotted in Figures 8 and 9, respectively. It is seen that the density has a high value even at t = 40 ns that means that with this spot size a pulse duration of 50 ns is reasonable. Figure 9 shows that one achieves a temperature of the order of 20 eV at t = 40 ns.

Density vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 1.0 mm, particle energy = 2.7 Gev/u and target radius = 0.4 mm.

Temperature vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 1.0 mm, particle energy = 2.7 Gev/u and target radius = 0.4 mm.

Spot size with FWHM 1.5 mm

In this case, we assume a target with a radius of 0.6 mm and chose the pulse length to be 100 ns. The results are plotted in Figures 10 and 11. The figures show that with such a spot size one may use a pulse length of 100 ns because there is no significant material expansion during major part of the irradiation time. Since the temporal power profile is considered to be parabolic, the bulk of the ions will be delivered in 80 ns. A temperature of the order of 13 eV is achieved in this case.

Density vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 1.5 mm, particle energy = 2.7 Gev/u and target radius = 0.6 mm.

Temperature vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 1.5 mm, particle energy = 2.7 Gev/u and target radius = 0.6 mm.

FURTHER DISCUSSION OF RESULTS AND THEIR IMPLICATIONS ON HED MATTER STUDIES

In this section, we discuss the implications of the calculations presented in the previous section on the HED matter research using an intense heavy ion beam.

An intense heavy ion beam can be employed using two very different schemes to study the thermophysical properties of HED matter. In the first case, a thin cylinder or a thin foil is isochorically heated by the beam and the heated material is allowed to expand isentropically. Numerical simulations have shown (Hoffmann et al., 2002) that while going through the expansion phase the heated material will pass through different interesting physical states. These include that of an expanded hot liquid, critical point region, two-phase liquid-gas region, or that of a strongly coupled plasma provided that sufficient specific energy is deposited in the target. To ensure uniform heating of the target material one assumes that the target length is much smaller than the ion range while the cylinder diameter or the foil thickness is much smaller than the FWHM of the Gaussian distribution of the energy power profile along the beam radius. This concept we call HIHEX (Heavy Ion Heating and Expansion). It is to be noted that in the HIHEX method, any significant expansion of the target material should be avoided during the heating phase. Therefore the option with a beam radius having a FWHM of 0.5 mm is not suitable for this scheme, unless the bunch length is reduced to 5 ns, which is not within the design parameters of the SIS100. If however in some cases the SIS100 operates at lower intensities, the option of using a beam focal spot with a FWHM of 0.5 mm will be useful with a pulse length of 20 ns.

The second scheme consists of imploding a sample material that is enclosed in a solid casing by a hollow beam that has an annular (ring shaped) focal spot. Detailed numerical simulations and analytic modeling (Tahir et al., 2001; Piriz et al., 2002b) have shown that using this scheme one can achieve a low entropy compression of hydrogen with physical conditions that are expected to exist at the interior of the Giant planets, Jupiter and Saturn. One can also compress water or ice and create conditions similar to the ice mantle of Uranus and Neptune. This scheme we call LAPLAS (Laboratory Planetary Science). Another important feature of this scheme is the possibility to study the problem of hydrogen metalization.

Creation of a beam heated region with an annular focal spot is a challenging problem. One proposal to generate the required annular focal spot geometry is to use a high frequency RF-wobbler which will rotate the beam rapidly. Detailed analytic and numerical studies (Piriz et al., 2003) have shown that one would require about 10 revolutions in order to achieve a high level of symmetry in the energy deposition. It has also been found that a beam spot with a FWHM of 1 mm would deposit enough energy in the target to lead to a high degree of compression. It has also been demonstrated experimentally that using a plasma lens one can also achieve a hollow beam with an annular focal spot (Neuner et al., 2000).

CONCLUSIONS

In this paper, we present numerical simulation results that have been performed in order to estimate the minimum pulse length and maximum power achievable at the SIS100 for three different values of particle energy (0.4 GeV/u, 1 GeV/u, and 2.7 GeV/u). These simulations have been done using a longitudinal dynamics particle in cell (PIC) code, ESME. It has been found that a pulse length in the order of 20 ns may be possible for all the above values of particle energy when no prebunching is performed while the pulse length gradually increases with the prebunching voltage. The worst case is for the kinetic energy of 0.4 GeV/u which leads to a pulse length of about 100 ns for a prebunching voltage of 100kV (RF amplitude). The peak power was found to have a maximum, however, at 0.5–1.5 kV prebunching voltage, depending on the mean kinetic energy of the ions.

Using the above information about the achievable values of pulse length under different conditions, we have also carried out numerical simulations of thermodynamic and hydrodynamic response of a cylindrical target made of solid lead that is irradiated by the SIS100 beam with full intensity. The purpose of this study is to determine an optimum value for the radius beam spot (FWHM of the Gaussian power distribution along the radius) corresponding to the pulse length range considered in the SIS100 design. Our conclusion is that the spot should not be less than 1 mm for a pulse length of 50 ns if the SIS100 is working at full intensity. Otherwise significant hydrodynamic expansion of the target will occur during the irradiation time that will make the target heating inefficient. If, on the other hand, for some reason the SIS100 is operating at a lower beam intensity, one may use a FWHM of 0.5 mm with a pulse length of 20 ns (Mustafin et al., 2002).

ACKNOWLEDGMENTS

The authors wish to thank the German Ministry of Research and Development (BMBF) for providing financial support to carry out this work.

References

REFERENCES

Bakhmetjev, I.E., Fertman, A.D., Golubev, A.A., Kantsyrev, A.V., Luckjashin, V.E., Sharkov, B.Yu., Turtikov, V.I., Kunin, A.V., Vatulin, V.V., Zidkiv, N.V., Baldina, E.G., Neuner, U., Wieser, J., Jacoby, J. & Hoffmann, D.H.H. (2003). Research into the advanced experimental methods for precision ion stopping range measurements in matter. Laser Part. Beam. 21, 1.Google Scholar
Bushman, A.V. & Fortov, V.E. (1987). Wide-range equation of state for matter under extreme conditions. Sov. Tech. Rev. B 1, 219.Google Scholar
Chao, Wu.A. & Tinger, M. (1998). Handbook of Accelerator Physics and Engineering. Maury Tigner (Ed.), Hackensack, NJ: World Scientist.
Deutsch, C. (1986). Inertial conferment fusion driven by intense heavy ion beams. Ann. Phys. Fr. 11, 1.CrossRefGoogle Scholar
Fortov, V.E., Goel, B., Munz, C.-D., Ni, A.L., Shutov, A. & Vorobiev, O.Yu. (1996). numerical simulations of non-stationary fronts and interfaces by the godunov method in moving grids. Nucl. Sci. Eng. 123, 169.CrossRefGoogle Scholar
Funk, U., Bock, R., Dornik, M., Geissel, M., Stetter, M., Stöwe, S., Tahir, N.A. & Hoffmann, D.H.H. (1998). High energy density in solid rare gas targets and solid hydrogen. Nucl. Instr. Meth. A 415, 68.CrossRefGoogle Scholar
Hasegawa, J., Yokoya, N., Kobayashi, Y., Yoshida, M., Kojima, M., Sasaki, T., Fukuda, H., Ogawa, M., Oguri, Y. & Murakami, T. (2003). Stopping power of dense helium plasma for fast heavy ions. Laser Part. Beam. 21, 7.CrossRefGoogle Scholar
Hoffmann, D.H.H., Weyrich, K., Wahl, H., Gardes, D., Bimbot, R. & Fleurier, C. (1990). Energy loss of heavy ions in plasma target. Phys. Rev. A 42, 2313.CrossRefGoogle Scholar
Hoffmann, D.H.H., Fortov, V.E, Lomonosov, I.V., Mintsev, V., Tahir, N.A., Varentsov, D. & Wieser, J. (2002). Unique Capabilities of Heavy Ion Beams as a Tool for Equation-of-State Studies. Phys. Plasmas 9, 3651.Google Scholar
MacLachlan, J. (1990). Fundamentals of particle tracking for longitudinal projection of beam phasespace in synchrotrons. Fermilab Note, FN-481, Batavia, IL.
Mehlhorn, T. (1981). A finite temperature model for ion energy deposition in ion driven inertial connement fusion targets. J. Appl. Phys. 52, 6522.CrossRefGoogle Scholar
Müller, R. & Spiller, P. (1996). Strategy for achieving high target power density with a modied sis18 and the new high current injector. GSI Rep. GSI-96-07.Google Scholar
Mustafin, E., Boine-Frankenheim, O., Hofmann, I. & Spiller, P. (2002). Beam losses in heavy ion drivers. Laser Part. Beam. 20, 637.CrossRefGoogle Scholar
Nardi, E. & Zinamon, Z. (1982). Charge state and slowing down of fast ions in plasmas. Phys. Rev. Lett. 49, 1251.CrossRefGoogle Scholar
Neuner, U., Bock, R., Constantin. C., Dewald, E., Funk, U., Geissel, M., Hakuli, S., Hoffmann, D.H.H., Jacoby, J., Kozyreva, A., Roth, M., Spiller, P., Tahir, N.A., Tauschwitz, A., Udrea, S., Varentsov, D., &Wieser, J. (2000). Shaping of intense ion beams into hollow cylindrical forms. Phys. Rev. Lett. 85, 4518.CrossRefGoogle Scholar
Piriz, A.R., Portugues, R., Tahir, N.A. & Hoffmann, D.H.H. (2002a). Implosion of multi-layered cylindrical targets driven by intense heavy ion beams interacting with solid targets. Phys. Rev. E 66, 485.Google Scholar
Piriz, A.R., Portugues, R., Tahir, N.A. & Hoffmann, D.H.H. (2002b). Analytic model for studying heavy ion imploded cylindrical targets. Laser Part. Beams 20, 427.Google Scholar
Stöwe, S., Bock, R., Dornik, M., Spiller, P., Stetter, M., Fortov, V.E., Mintsev, V., Kulish, M., Shutov, A., Yakushev, V., Sharkov, B., Golubev, A., Bruynetkin, B., Funk, U., Geissel, M., Hoffmann, D.H.H. & Tahir, N.A. (1998). High energy density plasmas with heavy ions. Nucl. Instr. Meth. A 415, 68.Google Scholar
Tahir, N.A., Hoffmann, D.H.H., Kozyreva, A., Shutov, A., Maruhn, J.A., Neuner, U., Tauschwitz, A., Spiller, P. & Bock, R. (2000a). Shock compression of condensed matter using intense heavy ion beams. Phys. Rev. E 61, 1975.Google Scholar
Tahir, N.A., Hoffmann, D.H.H., Kozyreva, A., Shutov, A., Maruhn, J.A., Neuner, U., Tauschwitz, A., Spiller, P. & Bock, R. (2000b). Equation ofstate properties of high-energy-density matter using intense heavy ion beams with an annular focal spot. Phys. Rev. E 62, 1232.Google Scholar
Tahir, N.A., Hoffmann, D.H.H., Kozyreva, A., Tauschwitz, A., Shutov, A., Maruhn, J.A., Neuner, U., Spiller, P., Roth, M., Jacoby, J., Bock, R., Juranek, H. & Redmer, R. (2001). Hydrogen metallization in heavy ion imploded multi-layered cylindrical targets. Phys. Rev. E 63, 016402-1-9.Google Scholar
Tahir, N.A., Shutov, A., Varentsov, D., Spiller, P., Udrea, U., Hoffmann, D.H.H., Lomonosov, I.V., Wieser, J., Kirk, M., Piriz, A.R., Fortov, V.E. & Bock, R. (2003a). Inuence of equation-of-state of matter and beam characteristics on target heating and compression. Phys. Rev. ST AB 6, 020101.Google Scholar
Tahir, N.A., Deutsch, C., Fortov, V.E, Gryaznov, V.K, Hofmann, D.H.H., Juranek, H., Lomonosov, I.V., Piriz, A.R., Redmer, R., Shutov, A., Spiller, P., Temporal, M., Udrea, U. & Varentsov, D. (2003b). Intense heavy ion beams as a tool to induce high-energy-density states in matter. Plasma Phys. 43, 373.Google Scholar
Temporal, M., Piriz, A.R., Grandjouan, N., Tahir, N.A. & Hofmann, D.H.H. (2003). Numerical analysis of multi-layered cylindrical target compression driven by a rotating intense heavy ion beam. Laser Part. Beams 21, 605.CrossRefGoogle Scholar
Varentsov, D., Tahir, N.A., Lomonosov, I.V., Hofmann, D.H.H., Wieser, J. & Fortov, V.E. (2003). Energy loss dynamics of intense uranium beam with solid neon for equation of state studies. Euro Phys. Lett. 64, 57.CrossRefGoogle Scholar
Ziegler, J.F., Biersack, J.P & Littmark, U. (1996). The Stopping and Ranges of Ions in Solids, New York: Pergamon Press.
Figure 0

SIS100 beam and machine parameters

Figure 1

Minimum pulse length at maximum compression versus Vinitial for 238U28+ at an intensity of 2 × 1012 ions. The energies quoted in the legend are those of the mean kinetic energy per nucleon of the ions. The smooth curves are only for visual guidance.

Figure 2

Peak pulse power versus Vinitial for 238U28+ at an intensity of 2 × 1012 ions. The energies quoted in the legend are those of the mean kinetic energy per nucleon of the ions.

Figure 3

Beam-Target geometry.

Figure 4

Density vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 0.5 mm, particle energy = 2.7 Gev/u and target radius = 0.2 mm.

Figure 5

Temperature vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 0.5 mm, particle energy = 2.7 Gev/u and target radius = 0.2 mm.

Figure 6

Density vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 5 ns, spot FWHM = 0.5 mm, particle energy = 2.7 Gev/u and target radius = 0.2 mm.

Figure 7

Temperature vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 5 ns, spot FWHM = 0.5 mm, particle energy = 2.7 Gev/u and target radius = 0.2 mm.

Figure 8

Density vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 1.0 mm, particle energy = 2.7 Gev/u and target radius = 0.4 mm.

Figure 9

Temperature vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 1.0 mm, particle energy = 2.7 Gev/u and target radius = 0.4 mm.

Figure 10

Density vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 1.5 mm, particle energy = 2.7 Gev/u and target radius = 0.6 mm.

Figure 11

Temperature vs. radius at different times, lead cylinder, irradiated with a uranium beam with an intensity of 2 × 1012 particles per bunch, bunch length = 50 ns, spot FWHM = 1.5 mm, particle energy = 2.7 Gev/u and target radius = 0.6 mm.