Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-06T07:46:21.823Z Has data issue: false hasContentIssue false
  • English
  • Français

Study on two-dimensional transfer of radiative heating wave

Published online by Cambridge University Press:  30 August 2005

KE LAN ,
TINGGUI FENG ,
DONGXIAN LAI ,
YAN XU  and
XUJUN MENG
KE LAN
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, China
TINGGUI FENG
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, China
DONGXIAN LAI
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, China
YAN XU
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, China
XUJUN MENG
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing, China
Rights & Permissions [Opens in a new window]

Abstract

A two-dimensional (2D) multigroup radiation transfer hydrodynamics code LARED-R-1 is used to simulate a supersonic wave experiment performed earlier by the Livermore group. The main result is that, contrary to the conclusion of Back et al. (2000a), the average-atom opacity model is sufficient to explain the obtained experimental results, provided that an adequate description of the radiation transport was used. The simulation results from LARED-R-1 show the spectrum of radiation in foam with radius and length of several optical depths is not in Planckian distribution and the angular intensity distribution is anisotropic.

Keywords

Anisotropic2D multigroup radiation transferRadiatively heated foamSupersonic wave
Type
Research Article
Information
Laser and Particle Beams , Volume 23 , Issue 3 , September 2005 , pp. 275 - 282
Copyright
© 2005 Cambridge University Press

1. INTRODUCTION

The study of supersonic heat wave propagation in matter driven by thermal radiation is important for many fields, such as inertial confinement fusion (Borisenko et al., 2003), Z-pinch (Chaikovsky et al., 2003), and heavy ion driven fusion (Barnard et al., 2003; Niemann et al., 2003). After the first work done by Marshak (1958), theoretical (Zel'dovich & Raizer, 1966; Kaiser et al., 1989), and experimental studies (Sigel et al., 1990; Schwanda & Eidmann, 1992) were done extensively on this subject. Low-density material foam (Basko & Meyer-ter-Vehn, 1993; Borisenko et al., 2003; Philippe et al., 2004) has come to play an important role as an efficient converter and hence, many experiments were done on supersonic heat wave propagation in foam (Afshar-rad et al., 1994; Massen et al., 1994; Back et al., 2000a, 2000b). Usually, it was assumed that the photons begin to thermalize at about one optical depth, that is, the emission is isotropic and the spectrum is in planckian distribution, so the diffusive approximation begins to be applicable. The diffusive approximation was therefore used very often to simulate the transfer process of supersonic wave in foam which is longer than one optical depth (Back et al., 2000a, 2000b). However, it is necessary to investigate this fundamental assumption closely by using a detail simulation tool which can give the spectrum and the angular intensity distribution in radiation transfer, such as a two-dimensional (2D) multigroup radiation transfer hydrodynamics code.

In this paper, we used LARED-R-1, a 2D multigroup radiation transfer hydrodynamics code, to simulate the supersonic wave in a radiatively heated SiO2 foam cylinder with radius and length of several optical depths, in order to study the spectrum and the angular intensity distribution in radiation transfer in this kind of foam. A S-N discrete ordinates method (Lewis & Miller, 1984; Menart, 2000) is used in LARED-R-1 to solve the radiative equation of transfer, so the spectrum and the angular intensity distribution can be obtained in the whole foam. In Section 2, we will introduce the model used in our simulation, and then compare the simulation results of LARED-R-1 with observations in Section 3. In Section 4, we will discuss the spectral distribution and the angular distribution of radiation in the SiO2 foam cylinder because they are of fundamental interest in the study of supersonic propagation. Finally, a conclusion will be presented in Section 5.

2. CODE AND MODEL

In LARED-R-1, hydrodynamic equations are coupled to radiation transfer equation. The methods used in the code are discussed in other papers (Feng, 1995; Feng et al., 1999, 2001). The equations of electron temperature Te and ion temperature Ti in 2D cylindrical coordinate are:

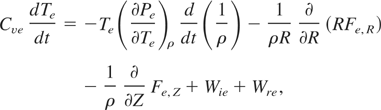
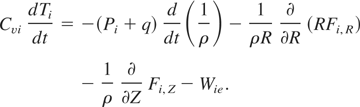
In the above equations, t is time, Cve and Cvi are respective specific heat of electron and ion, Pe is electron pressure, Pi is ion pressure, q is artificial viscosity, R is spatial position, ρ is mass density, Fe,R and Fe,Z are electron energy fluxes due to thermal conduction in radial direction and axial direction, respectively, Fi,R and Fi,Z are energy fluxes for ion, Wie is electron-ion energy exchange, and Wre is electron-photon energy exchange.

The 2D radiation transfer equation is:

Here, Iν is the specific intensity of radiation at radial position R and axial position Z, traveling in direction Ω, with frequency ν and at time t. The directional coordinate system is shown in Figure 1. As shown, θ is the angle of Ω with Z axis and ω is that with the radial direction R. The symbols u is plasma velocity, μν′ is effective absorption coefficient, Bν is planckian function, Sν is source function, and σth is Thomson scattering absorption coefficient.

Directional coordinate system. Here, Ω is the travel direction of photons, θ is the angle of Ω with z axis, and ω is that with the radial direction.

The model used in our simulation is chosen from the experiment done by Back et al. (2000a). According to their experiments, a SiO2 foam cylinder of 3 mm diameter and 10 mg/cm3 density was cast into a 25 μm thick Au ring of three different lengths: 0.5, 1.0, and 1.5 mm. Figure 2 is a schematic of the SiO2 foam and the Au ring. The X-ray radiation wave propagates axially down the cylindrical foam and finally breaks out of the exterior face. We define six characteristic positions in the figure, which are denoted by Oi and Ei (i = 1,3). O1 and E1 are in the middle of the foam cylinder; O3 and E3 are on the exterior face; and O2 and E2 are 50 μm axially away from the exterior face. Oi (i = 1,3) are on the axis of the foam cylinder, while Ei (i = 1,3) are at the edge. The simulation results at these characteristic positions will be presented in Sections 3 and 4.

Schematic of the SiO2 foam and the Au ring. Here, we define six characteristic positions which are denoted by Oi and Ei (i = 1,3). O1 and E1 are in the middle of the foam cylinder; O3 and E3 are on the exterior face; and O2 and E2 are 50 μm axially away from the exterior face. Oi (i = 1,3) is at the center of the foam cylinder, and Ei (i = 1,3) is at the edge.

The X-ray driven temperature used in our simulation is fitted from the measured Tr (Back et al., 2000a), as shown in Figure 3. In this simulation, an averaged atom model is used to supply opacities, and S-4 method (three discrete directions per octant) is used to solve the radiative equation of transfer. There are 100 frequency groups used, from 0 to 3 × 104 eV.

Temperature dependent mean free path (MFP) at 250 eV and Rosseland MFP in a 10 mg/cm3 SiO2.

3. SIMULATION RESULTS AND COMPARISON WITH EXPERIMENTS

Because opacity is essential for radiative transfer study, we first compared the opacity obtained by using our average atom model with that given by Back et al. (2000a). Figure 3 is the temperature dependent mean free path (MFP) at hν = 250 eV and Rosseland MFP in a 10 mg/cm3 SiO2, obtained by using our average atom model. Here, h is the Planckian constant and ν is the photon frequency. From Figure 3, the MFP at 250 eV is about 40 μm over a wide temperature range, from the cold to 60 eV; and the Rosseland MFP is 230–450 μm over the 40–60 eV. There are some differences between the values above and that given by Back et al. (2000a). The cold MFP at 250 eV is 40 μm and rises to 50–100 μm at the temperature from 40 to 60 eV, and the Rosseland MFP is 230–550 μm over the 45–60 eV. However, the differences are not remarkable (Back et al., 1992).

3.1. Breakout time

Foam emission at hν = 250 eV with a spectral bandwidth of about 10 eV was measured and its breakout times at the center of the three different length foams were given (Back et al., 1992). To compare the simulation results of LARED-R-1 with that measured from the experiments, we choose the spectra range from hν = 245 eV to 255 eV as a photon group in our simulation. The simulated intensities at hν = 250 eV vs. time lineouts at O3 and E3 of the 0.5, 1.0, and 1.5 mm long SiO2 foams are shown in Figure 4. As presented, the simulated breakout times tbk at the center of exterior face are 4.7, 7.5, and 10.8 ns for foams of the three different lengths, and are, respectively, 5.2, 8.8, and 12.8 ns at the edge of the foams.

Simulated intensity at hν = 250 eV vs. time on O3 (thick solid lines) and E3 (thin solid lines) of the 0.5, 1.0, and 1.5 mm long SiO2 foams. Dotted line is the radiation drive temperature fitted from the experimental result shown in Back et al. (2000a). The unit of the intensity is arbitrary unit (a.u.), and this is the same in the following figures.

Figure 5 is a radial lineout at 9.5 ns after the X-ray drive started for the 1.0 mm long foams. From Figures 4 and 5, the radiation wave breaks out the center prior to breaking out at the edge, and there is a remarkable curvature in the radiation front. These simulation results agree with Back et al. (2000a). An analysis was given for the phenomena (Back et al., 2000a). Here, we just want to emphasize that the energy loss into the heating wall ring is the main reason for the curvature in radiation wave front and breakout timing difference.

Simulated Tr and radial lineout of hν = 250 eV on the center of the exterior face O3 at the time of 9.5 ns for a 1.0 mm long foam.

In Back et al. (2000a), experimental data of radial lineout at 9.5 ns and the simulation results by using both detailed OPAL opacity model and an average atom model were presented. Comparing Figure 4 in Schwanda and Eidmann (1992) with Figure 4 here, we can see that simulation results of LARED-R-1 by using average atom model is near the simulation results of Back et al. (2000a) by using detailed OPAL opacity model, and fit well with the intensity data. The result is quite different from the conclusion made by Back et al. (2000a), in which it obtained a planar radiation wave front when the average atom model was used in their simulation, and this was imputed to the average atom model in Back et al. (2000a). Nevertheless, from the simulation results of LARED-R-1, the diffusive approximation plays a more important role in influencing the simulation result than an atomic model, and their simulation result which disagreed with the experiments should be mainly due to the diffusive approximation. We therefore conclude that the multigroup radiation transfer is much more reasonable than the diffusive approximation in simulating the transfer process of the supersonic wave in foam. Moreover, based on the simulation results of Back et al. (2000a), we can expect a much better simulation result from LARED-R-1 if a detailed OPAL opacity model is used. Our detailed OPAL opacity model is under development, and we will show the simulation results of LARED-R-1 by using the detailed OPAL opacity model in another paper.

3.2. The equivalent radiation temperature Tr and the electron temperature Te

3.2.1. The radial distribution of Tr on exterior face

We define the equivalent radiation temperature Tr = (Er /a)1/4. Here, Er is the energy density of radiation and a is the classical radiation constant. We use m to express the mth discrete direction and define Ig,m = ∫Δνg Iν(R,z,Ωm,t) dν, then we have Er = (1/c)[sum ]g [sum ]m Ig,m Pm. Here, Iν(R,z,Ωm,t) is the specific intensity at frequency ν as a function of radial position R, axial position z, the mth discrete direction Ωm and time t. The symbols Pm is the weight for the mth discrete direction and c is the speed of light. The radial distribution of Tr at the exterior face is given in Figure 4. As shown, Tr decreases much slower along the radial direction than the intensity. By using a simple scaling of tbk (Back et al., 2000a) and the opacity data from our average atom model, we have tbk ∝ Tr−5.2. Therefore, tbk changes remarkably although Tr changes little from the center to the edge.

3.2.2. Spatial distribution of Te and Tr in the R-Z plane

Shown in Figure 6 are spatial distributions of electron temperature Te and the equivalent radiation temperature Tr in the R-Z plane at the times of 4 ns and 9.5 ns for the 1 mm long foam. As it is shown, Te is much lower than Tr at the same spatial point at 4 ns, but they are almost the same at 9.5 ns. Furthermore, we can see clearly from Figure 6(a) to 6(d) that there are significant curvatures of Te and Tr distributions along radial direction.

Spatial distributions of Te and Tr in R-Z plane at the times of 4 ns and 9.5 ns. (a) Tr at 4 ns; (b) Te at 4 ns; (c) Tr at 9.5 ns; (d) Te at 9.5 ns.

3.2.3. Relaxation time between Te and Tr

Figures 7(a) and 7(b) are time evolutions of Te and Tr on O1, E1, O2, and E2 of the 1 mm long foam. We define the relaxation time tre as the time when Te almost equals Tr at the same point, then tre = 4.7 ns, 5.3 ns, 7.5 ns, and 8.7 ns on O1, E1, O2, and E2, respectively. Therefore, tre is shorter at the center than at the edge.

Temporal electron temperature Te (solid lines) and the equivalent radiation temperature Tr (dashed lines) on (a) O1 and E1, and (b) O2 and E2 of the 1 mm long foam. Dotted lines are the radiation drive temperature.

However, the real spectral distribution is far from Planckian distribution even after tre, and more, the angular distribution of the intensity is significantly inhomogeneous, which will be discussed in the following sections. We will use the 1 mm long foam as an example, which is about two Rosseland MFP in length.

3.3. Expansion of Au wall at the source entrance

Expansion of Au wall may make the entrance smaller and obscure the X-ray source. From the simulation results of LARED-R-1, the expansion of the Au wall is insensitive to the length of the foam, and it expands inward about 200 μm at 9.5 ns. This agrees with the experimental results given in Back et al. (2000a).

4. SPECTRAL AND ANGULAR DISTRIBUTIONS

4.1. Spectral distribution

First, we compared the spectral distribution in SiO2 foam with the blackbody spectral distribution Bν(Tr). From Planckian relation, we have Bν(Tr) = (2hν3/c2) [1/ehν/(kTr) − 1]. The angular averaged spectral distribution 1/4πΔνg [sum ]m Ig,m Pm is given by LARED-R-1.

In Figure 8, we present the comparisons of (1/4πΔνg) [sum ]m Ig,m Pm with Bν(Tr) at times of 6 ns and 9.5 ns at the center point O2 which is just near the exterior face. As shown, the spectral distribution in SiO2 is far from the blackbody distribution at 6 ns, but they are near to 9.5 ns. Nevertheless, a remarkable difference still exists even at 9.5 ns.

Comparisons of the spectral distribution (solid line) with Planckian distribution (dashed line) on O2 of the 1 mm long foam. (a) 6 ns; (b) 9.5 ns. The calculated spectral distribution consists of a sequence of discrete points, each representing the corresponding sum over angles for the corresponding spectral group. The points are not plotted in the figure because the number of spectral groups is large, which is 100. The Planckian distributions have kinks at about hν = 250 eV and 500 eV, because they are calculated also at those discrete points and the group steps are big at these points. This is the same in Fig. 9.

We further compare (1/4πΔνg)[sum ]m Ig,m Pm with Bν(Tr) at 9.5 ns at points O1, E1, and E2 in Figure 9. As presented, the spectrum is always harder than the blackbody distribution. The reason for this lies in the fact that the photon with high energy has a longer MFP and is easier to propagate than the photon with lower energy. Moreover, we noticed from Figure 8(b) that the spectral distribution at E1 is very near the blackbody distribution when we compare it with other points. From Figure 2, E1 is on the interface between SiO2 and Au, and it is in the middle of the cylinder. We will see from Figure 10(b) that the radiation at E1 mainly comes from the Au wall which emission is almost in blackbody distribution.

Comparisons of the spectral distribution (solid line) with Planckian distribution (dashed line) at 9.5 ns on the three characteristic points of (a) O1, (b) E1 and (c) E2. The length of the foam is 1 mm. More explanation of the lines is given in Fig. 8.

Angle distributions of the intensity at 8 ns (square), 9.5 ns (triangle), and 12 ns (circle) on the characteristic points of (a) O1, (b) E1, (c) O2 and (d) E2 of the 1 mm long foam. The (θ,ω) of m = 1 to 12 are: (150.3°,135°), (110.5°,158°), (110.5°,112°), (150.3°,45°), (110.5°,68°), (110.5°,22°), (29.7°,135°), (69.5°,158°), (69.5°,112°), (29.7°,45°), (69.5°,68°), (69.5°,22°).

4.2. Angular intensity distribution in foam

By using S-4 discrete ordinates method to solve the radiative equation of transfer, LARED-R-1 can give the angular intensity distribution in 12 discrete directions for all photon groups. The 12 discrete directions are shown in the figure caption of Figure 10. As shown, θ is 29.7° for m = 7 and 10, 69.5° for m = 8, 9, 11, and 12, 150.3° for m = 1 and 4, and 110.5° for m = 2, 3, 5, and 6. Hence, the photon in the directions of m = 7 − 12 propagates down the cylindrical foam to the exterior face; while the photon in m = 1 − 6 propagates up to the entrance face. On the other hand, ω < 90° for m = 4, 5, 6, 10, 11, and 12, so photons in these directions propagate outward to the Au wall; while ω > 90° for m = 1, 2, 3, 7, 8, and 9, so photons in these directions propagate toward the inner part of the SiO2 foam.

Figure 10(a) to 10(d) give the angular intensity distributions at 8 ns, 9.5 ns, and 12 ns, on the center points O1 and O2 and at the edge points E1 and E2. In Figure 10(d), the intensity distribution at 8 ns is not presented because the emission on E2 at this time is too weak to be shown. From Figure 10, we can obtain the following conclusions on angular intensity distribution in foam. (1) The intensity is anisotropic throughout the whole foam cylinder, which is two Rosseland MFP in length and three in radius, irrespective of the center, the edge, the middle, or the exterior face. However, it is axis-symmetrically on axis. (2) Emission propagating down (m = 7 − 12) is stronger than those up (m = 1 − 6) toward the entrance, due to the different boundary conditions on the left and the right of the foam cylinder. It is the X-ray driven source on the left of the foam, while it is the vacuum on the right. Especially at the centers, the emission at m = 7 and 10 is the strongest while that at m = 1 and 4 is the weakest. This is due to their small angle with the positive or negative z axis, and hence the emission is strongly influenced by the boundary conditions. (3) On centers O1 and O2 which are respective one and two Rosseland MFP away from the X-ray entrance, intensity is stronger when θ is smaller. This suggests that the radiations at these points are mainly contributed by transmission of the X-ray source. This is also known from the spectrum at these points, which is harder than the Planckian distribution. Hence, transmission of the X-ray drive in this model, after two Rosseland MFP, is still stronger than re-emission of SiO2 foam and Au wall.

4.3. Angular intensity distribution on the exterior face

In this part, we further discuss the angular intensity distribution on the exterior face of the foam because it is very important in the measurements. Figure 11(a) and 11(b) are the angular intensity distribution at 250 eV on the center point O3 and the edge point E3 on the exterior surface of the 1 mm long foam, at 6, 9.5, and 12 ns. As it is shown, (1) On the center O3, the angular intensity distribution is axisymmetric and the intensity is stronger when θ is smaller. At 9.5 ns, the radiation in m = 7 is 30% stronger than in m = 8 and 9. (2) At the edge E3, it is seriously anisotropic. The intensity in m = 10 is more than 12 times stronger than that in m = 8 at 9.5 ns. The radiation in m = 10, 11, and 12 is mainly the transmission of X-ray source, and that in m = 7, 8, and 9 is contributed merely by the re-emission of Au wall. Obviously, the transmission of X-ray source is stronger than re-emission of Au wall.

Angle distributions of the intensity at 8 ns (square), 9.5 ns (triangle), and 12 ns (circle) on the characteristic points of (a) O3 and (b) E3 of the 1 mm long foam.

5. CONCLUSION

The simulation results from the 2D multigroup radiation transfer hydrodynamics code LARED-R-1 agree well with the observations of the supersonic wave experiment done earlier by the Livermore group. However, our simulation shows that, contrary to the conclusion of Back et al. (2000a), the average-atom opacity model is sufficient to explain the obtained experimental results, provided that an adequate description of the radiation transport was used. Based on the simulations, two important conclusions are obtained. First, the radiation spectrum in the foam is harder than Planckian distribution because the photon of higher energy has a longer MFP. Second, the radiation is anisotropic throughout the whole foam cylinder due to the different boundary conditions on the two cylinder surfaces. This suggests that the diffusive approximation is not suitable for the close investigation of the supersonic wave transfer process in foam. This will be more clear if a comparison between the results from LARED-R-1 and that from a 2D multigroup diffusive radiation transfer code can be made by using the same opacity model. However, we don't have a 2D multigroup diffusive radiation transport hydrodynamics code at present, so this work will be done in the future.

References

REFERENCES

Afshar-rad, T., Desselberger, M., Dunne, M., Edwards, J., Foster, J.M., Hoarty, D., Jones, M.W., Rose, S.J., Rosen, P.A., Taylor, R. & Willi, O. (1994). Supersonic propagation of an ionization front in low density foam targets driven by thermal radiation. Phys. Rev. Lett. 73, 74.CrossRefGoogle Scholar
Back, C.A., Bauer, J.D., Landen, O.L., Turner, R.E., Lasinski, B.F., Hammer, J.H., Rosen, M.D., Suter, L.J. & Hsing, W.H. (2000a). Detailed measurements of a diffusive supersonic wave in a radiatively heated foam. Phys. Rev. Lett. 84, 274.Google Scholar
Back, C.A., Bauer, J.D., Hammer, J.H., Lasinski, B.F., Turner, R.E., Rambo, P.W., Landen, O.L., Suter, L.J., Rosen, M.D. & Hsing, W.H. (2000b). Diffusive, supersonic x-ray transport in radiatively heated foam cylinders. Phys. Plasmas 7, 2125.Google Scholar
Barnard, J.J., Ahle, L.E., Bieniosek, F.M., Celata, C.M., Davidson, R.C., Henestroza, E., Friedman, A., Kwan, J.W., Logan, B.G., Lee, E.P., Lund, S.M., Meier, W.R., Sabbi, G.L., Seidl, P.A., Sharp, W.M., Shuman, D.B., Waldron, W.L., Qin, H. & Yu, S.S. (2003). Integrated experiments for heavy ion fusion. Laser Part. Beams 21, 553–560.CrossRefGoogle Scholar
Basko, M.M. & Meyer-ter-Vehn, J. (1993). Hotraum target for heavy ion inertial fusion. Nucl. Fusion 33, 601.CrossRefGoogle Scholar
Borisenko, N.G., Akunets, A.A., Bushuev, V.S., Dorogotovtsev, V.M. & Merkuliev, Y.A. (2003). Motivation and fabrication methods for inertial confinement fusion and inertial fusion energy targets. Laser Part. Beams 21, 505–509.Google Scholar
Chaikovsky, S.A., Labetsky, A.Y., Oreshkin, V.I., Shishlov, A.V., Baksht, R.B., Fedunin, A.V. & Rousskikh, A.G. (2003). The K-shell radiation of a double gas puff z-pinch with an axial magnetic field. Laser Part. Beams 21, 255–264.Google Scholar
Feng, T. (1995). Coupling transport diffusion method of calculating radiation transfer in a cavity. Comp. Phys. 12, 375 (in Chinese).Google Scholar
Feng, T., Lai, D. & Xu, Y. (1999). An artificial iteration method for calculating multi-group radiation transfer problems. Comp. Phys. 16, 199 (in Chinese).Google Scholar
Feng, T., Lan, K. & Lai, D. (2001). A comparison between two averaging methods of multi-group parameters in ICF radiation transfer calculation. Comp. Phys. 18, 206 (in Chinese).Google Scholar
Kaiser, N., Meyer-ter-Vehn, J. & Sigel, R. (1989). The X-ray-driven heating wave. Phys. Fluids B 1, 1747.CrossRefGoogle Scholar
Lewis, E.E. & Miller, W.F., Jr. (1984). Computational Methods of Neutron Transport. New York: Wiley.
Marshak, R.E. (1958). Effect of Radiation on Shock Wave Behavior. Phys. Fluids 1, 24.CrossRefGoogle Scholar
Massen, J., Tsakiris, G.D., Eidmann, K., Foldes, I.B., Lower, Th., Sigel, R., Witkowski, S., Nishimura, H., Endo, T., Shiraga, H., Takagi, M., Kato, Y. & Nakai, S. (1994). Supersonic radiative heat waves in low-density high-Z material. Phys. Rev. E 50, 5130.CrossRefGoogle Scholar
Menart, J. (2000). Radiative transport in a two-dimensional axissymmetric thermal plasma using the S-N discrete ordinates method on a line-by-line basis. J. Quant. Spectro. Rad. Transfer 67, 273.Google Scholar
Niemann, C., Penache, D., Tauschwitz, A., Rosmej, F.B., Neff, S., Birkner, R., Constantin, C., Knobloch, R., Presura, R., Yu, S.S., Sharp, W.M., Ponce, D.M. & Hoffmann, D.H.H. (2003). Diagnostics of discharge channels for neutralized chamber transport in heavy ion fusion. Laser Part. Beams 21, 13–15.Google Scholar
Philippe, F., Canaud, B., Fortin, X., Garaude, F. & Jourdren, H. (2004). Effects of microstructure on shock propagation in foams. Laser Part. Beams 22, 171–174.CrossRefGoogle Scholar
Schwanda, W. & Eidmann, K. (1992). Observation of radiative burnthrough in X-ray heated beryllium by time-resolved spectroscopy. Phys. Rev. Lett. 69, 3507.CrossRefGoogle Scholar
Sigel, R., Tsakiris, G.D., Lavarenne, F., Massen, J., Fedosejevs, R., Meyer-ter-Vehn, J., Murakami, M., Eidmann, K. & Witkowski, S. (1990). Experimental observation of laser-induced radiation heat waves. Phys. Rev. Lett. 65, 587.CrossRefGoogle Scholar
Zel'dovich, Ya.B. & Raizer, Yu.P. (1966). Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. New York: Academic.
Figure 0

Directional coordinate system. Here, Ω is the travel direction of photons, θ is the angle of Ω with z axis, and ω is that with the radial direction.

Figure 1

Schematic of the SiO2 foam and the Au ring. Here, we define six characteristic positions which are denoted by Oi and Ei (i = 1,3). O1 and E1 are in the middle of the foam cylinder; O3 and E3 are on the exterior face; and O2 and E2 are 50 μm axially away from the exterior face. Oi (i = 1,3) is at the center of the foam cylinder, and Ei (i = 1,3) is at the edge.

Figure 2

Temperature dependent mean free path (MFP) at 250 eV and Rosseland MFP in a 10 mg/cm3 SiO2.

Figure 3

Simulated intensity at hν = 250 eV vs. time on O3 (thick solid lines) and E3 (thin solid lines) of the 0.5, 1.0, and 1.5 mm long SiO2 foams. Dotted line is the radiation drive temperature fitted from the experimental result shown in Back et al. (2000a). The unit of the intensity is arbitrary unit (a.u.), and this is the same in the following figures.

Figure 4

Simulated Tr and radial lineout of hν = 250 eV on the center of the exterior face O3 at the time of 9.5 ns for a 1.0 mm long foam.

Figure 5

Spatial distributions of Te and Tr in R-Z plane at the times of 4 ns and 9.5 ns. (a) Tr at 4 ns; (b) Te at 4 ns; (c) Tr at 9.5 ns; (d) Te at 9.5 ns.

Figure 6

Temporal electron temperature Te (solid lines) and the equivalent radiation temperature Tr (dashed lines) on (a) O1 and E1, and (b) O2 and E2 of the 1 mm long foam. Dotted lines are the radiation drive temperature.

Figure 7

Comparisons of the spectral distribution (solid line) with Planckian distribution (dashed line) on O2 of the 1 mm long foam. (a) 6 ns; (b) 9.5 ns. The calculated spectral distribution consists of a sequence of discrete points, each representing the corresponding sum over angles for the corresponding spectral group. The points are not plotted in the figure because the number of spectral groups is large, which is 100. The Planckian distributions have kinks at about hν = 250 eV and 500 eV, because they are calculated also at those discrete points and the group steps are big at these points. This is the same in Fig. 9.

Figure 8

Comparisons of the spectral distribution (solid line) with Planckian distribution (dashed line) at 9.5 ns on the three characteristic points of (a) O1, (b) E1 and (c) E2. The length of the foam is 1 mm. More explanation of the lines is given in Fig. 8.

Figure 9

Angle distributions of the intensity at 8 ns (square), 9.5 ns (triangle), and 12 ns (circle) on the characteristic points of (a) O1, (b) E1, (c) O2 and (d) E2 of the 1 mm long foam. The (θ,ω) of m = 1 to 12 are: (150.3°,135°), (110.5°,158°), (110.5°,112°), (150.3°,45°), (110.5°,68°), (110.5°,22°), (29.7°,135°), (69.5°,158°), (69.5°,112°), (29.7°,45°), (69.5°,68°), (69.5°,22°).

Figure 10

Angle distributions of the intensity at 8 ns (square), 9.5 ns (triangle), and 12 ns (circle) on the characteristic points of (a) O3 and (b) E3 of the 1 mm long foam.