1. INTRODUCTION
The efficient laser-plasma coupling opens the way for various exciting laser-plasma applications like particle acceleration (Bari et al., Reference Bari, Sheng, Wang, Li, Salahuddin, Nasim, Shabbir Naz, Gondal and Zhang2010) and laser fusion (Badiei et al., Reference Badiei, Andersson Patrik and Holmlid2010) radiation sources (Yang et al., Reference Yang, Ma, Shao, Xu, Yu, Gu, Yu, Yin, Tian and Kawata2010; Badziak et al., Reference Badziak, Jaboski, Parys, Szydowski, Fuchs and Mancic2010). All these need an efficient coupling between laser and plasma and instabilities are fundamental issues in the laser-plasma coupling. It is seen that, in the underdense region, large scattering (Starodub et al., Reference Starodub, Borisenko, Fronya, Merkuliev, Osipov, Puzyrev, Sahakyan, Vasin and Yakushev2010) of the laser can occur provided the laser power go beyond a certain threshold value; the threshold power is often exceeded in laser plasma experiments. In such cases, SBS (Huller et al., Reference Huller, Masson-Laborde, Pesme, Labaune and Bandulet2008; Hasi et al., Reference Hasi, Gong, Lu, Lin, He and Fan2008; Kappe et al., Reference Kappe, Strasser and Ostermeyer2007; Wang et al., Reference Wang, Lu, He, Zheng and Zhao2009) is of the special interest since it leads to large reflection losses. SBS is a parametric instability corresponding to the decay of an incident electromagnetic pump wave into an ion sound wave, and a second electromagnetic wave with lower frequency propagating in different direction. Although SBS has been the subject of extensive studies, both theoretically and experimentally, but many features of the experimental results do not agree with the theoretical prediction. These include low levels of SBS scattered light (Rozmus et al., Reference Rozmus, Sharma, Samson and Tighe1987). The theoretical analysis predicts high nonlinear reflectivity, but the laboratory experiments show that the reflectivity is some what lesser than the theoretical prediction (Baldis et al., Reference Baldis, Villeneuve, Fontaine, Enright, Labaune, Baton, Mounaix, Pesme, Casanova and Rozmus1993). To resolve the discrepancy between theoretical expectations and experimental (Gao et al., Reference Gao, Lu, Wang, He and Hasi2010) results, nearly all of the theoretical studies are focused with the saturation effects of SBS-driven IAW.
Most of the work on SBS deals with the propagation and transmission of laser beams in the paraxial approximation, because in the majority of cases, the divergence angles of the investigated laser beams are very small, and the beam widths of the investigated laser beams are far greater than the wavelength. Therefore, the paraxial wave equation gives an accurate description for wave beams near the axis as long as the beam width remains larger than the radiation wavelength λ throughout the propagation. However, in some experimental situations, it is necessary to go beyond the paraxial approximation, like the use of diffractive optical elements that present small features or of tightly focusing laser beams to reach the nonlinear range of intensities may lead to optical fields that cannot be described within the paraxial approximation. In addition to that, recent advances in laser technology, based on the chirped pulse amplification technique, make intensities greater than 1018 W/cm2 available for experiments. In these experiments, the laser beam power can be 1000 times larger than the critical value and one can expect multiple filamentation, focusing up to the point where the paraxial approximation breaks down in every filament and radiation scatters.
In this work, we examined the ponderomotive self focusing/filamentation of the laser beam with paraxial and modified paraxial approximation. The paraxial approximation has been modified by including fourth power of radial distance r. The higher order terms in the expansion of dielectric constant and eikonal have been taken into account. The laser intensity profile and other relevant quantities of plasma were also expended and it makes a significant difference in the study of propagation of laser beam in plasma (Liu & Tripathi). It is observed that in extended paraxial case, the filaments of the laser beam have been spitted and these modified structures affects the IAW generation. Therefore, SBS has been studied for both paraxial and modified paraxial cases and it is observed that in presence of off-axis part reflectivity of SBS is affected significantly.
The outline of this work is as follows: In Section 2, we have given the expression for the beam width parameter of the high power laser beam and modified equations for the excitation of the IAW when ponderomotive nonlinearity is operative by including the extended paraxial contribution. In Section 3, the basic equations that govern the dynamics of SBS process are given by considering the modified paraxial approximation. The SBS reflectivity has been compared for both paraxial and extended paraxial case in this section. Discussion of the results is presented in Section 4. The conclusions are given in the last section.
2. PROPAGATION OF LASER BEAM AND EXCITATION OF IAW
A high power Gaussian laser beam (pump) of frequency ω0 and wave number k 0 is assumed to be propagating in hot collisionless homogeneous plasma along the z axis. The wave equation governing the electric field of the laser beam in plasma can be written as
where 
is the high frequency current density vector, further assuming the variation of electric field 
of the laser beam as
with
where E 0 is a complex function of space, S 0 is the eikonal, ε0 is the linear part of the plasma dielectric constant. Substituting the value of j in the Eq. (1) and separating the real and imaginary parts of the resulting equation, we solve the real part equation by assuming E 0 and S 0 (by including the r 4 coefficients) in the extended paraxial approximation as, following (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Sodha et al., Reference Sodha, Ghatak and Tripathi1976; Sharma al., Reference Sharma and Sharma2009)
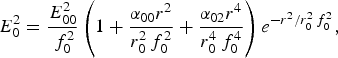
where E 00 is the axial amplitude, α00 and α02 are the coefficients of r 2 and r 4, respectively, and S 00 and S 02 both are the slowly varying function of r and z, using the normalized distance ξ = zc/ω0r 02, the laser beam width parameter f 0 governed as (Sharma et al., Reference Sharma, Sharma and Chauhan2007)
with the following equations (Sharma et al., Reference Sharma, Sharma and Chauhan2007)
where R d0 = k 0r 02, ξ = z/R d0. Eq. (4) gives the intensity profile of the laser beam in the plasma along with the radial direction when ponderomotive nonlinearity is operative. Numerical computation of Eq. (4) has been performed with the help of Eqs. (6)–(9).
When laser beam propagates in the plasma, its nonlinear interaction with the seed of IAW excites IAW. The excitation process of this IAW is investigated in the presence of the laser beam having a modified profile. Combining the standard fluid equations we get the general equation governing the ion density variation as
![\eqalign{\displaystyle{{\partial ^2 n_{is} } \over {\partial t^2 }} &+ 2\Gamma _i \displaystyle{{\partial n_{is} } \over {\partial t}} - c_s^2 \nabla ^2 n_{is} + k^2 c_s^2 \cr & \left[{ - 1+\left({{1 / {1 + k^2 {\rm \lambda} _d^2 \left({\displaystyle{{N_{0e} } \over {N_{00}^{} }}} \right)^{ - 1} }}} \right)} \right]n_{is} = 0 \comma }](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461100084X_eqn10.gif?pub-status=live)
The solution of the above equation can be written as
![n_{is} = n\left({r\comma \; z} \right)\exp \left\{{i\left[{{\rm \omega} t - k\left({z + S\left({r\comma \; z} \right)} \right)} \right]} \right\}\, \comma \;](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461100084X_eqn11.gif?pub-status=live){kind=small}
with the Debye length λd as
where Γi Landau damping coefficient for IAW, n is the real function of r and z, T 0 is the equilibrium temperature of the plasma, N 0e is the electron concentration in the presence of the laser beam, N 00 is the electron density in the absence of the beam, k β is the Boltzman's constant, and c s = (k βT e/M)1/2 is the speed of the IAW. The wave number k of the IAW satisfy the following dispersion relation in the presence of laser beam
Following Sharma et al. (Reference Sharma, Sharma, Rajput and Bhardwaj2009) and Sharma, P. et al. (Reference Sharma, Sharma, Rajput and Bhardwaj2009), we assume the initial radial variation of IAW density perturbation to be Gaussian, substituting (11) in (10) and the solution of the resulting equation at finite z may be written as
and
where k id = Γiω/kc s2 is the damping factor, a is the initial beam width of the acoustic wave, coefficients α 0i, etc. functions same as α 00 etc. functions in the previous section and f is a dimensionless beam width parameter of IAW governed as (Sharma, P. et al., Reference Sharma, Sharma, Rajput and Bhardwaj2009)
where R d = ka 2 is the diffraction length of the IAW and the equations for S 2i, α0i, α2i are as follows
and the coefficient α 0i and α2i as
Eq. (14) represents the density profile of IAW in the plasma when the coupling between laser beam and IAW is taken into account.
We have solved Eq. (14) numerically with the help of Eq. (16)–(19) to obtain the density perturbation at finite z. The result is shown in Figure 3, for typical laser parameters given in the discussion section, we have used in previous section. It is evident from the figure that the IAW gets excited due to nonlinear coupling with the high power laser beam because of the ponderomotive nonlinearity.
The nonlinear evolution of IAW may play an important role in SBS process. Stimulated scattering always involves a pump laser beam and a frequency-shifted scattered wave, coupled by either molecular vibrational transitions (Raman) or acoustic waves (Brillouin). SBS is mainly driven by the acoustic waves excited by an intense laser pulse.
Here, we are considering the special case where the restriction on laser beam profile and therefore off-axial rays are also taking part in the propagation. Due to the presence of the off-axial rays, the profile of the laser beam has been modified. Further, the modified profile of the laser beam affects the amount of energy scattered by the IAW and hence SBS. Therefore, it is necessary to model the interplay between SBS and the modified laser beam profile, which has not been addressed so far. In the next section, we develop the theory of SBS in the presence of modified profile of laser beam due the contribution of the off-axial rays.
3. FORMULATION: STIMULATED BRILLOUIN SCATTERING
The total electric field E T, may be written as the sum of the electric field E of the pump laser beam andE S, the electric field of the scattered wave, i.e.,
E S arises on account of scattering of the pump beam off the IAW, i.e., Brillouin scattering. The vector E T satisfies the wave equation
where J T is the total current density vector in the presence of the high frequency electric field E T. Equating the zero-th order terms in above equation, one obtains equation for the field inside the plasma i.e.,
and equating the terms at scattered frequency we get
In solving Eq. (22), the term ∇ (∇ · E) may be neglected in the comparison to the ∇2E S term. Let the solution of Eq. (22) i.e., E S is the electric field of the scattered wave
and
where
and k S1 and ωS satisfy the phase matching conditions
Following (Sharma et al., Reference Sharma, Sharma, Rajput and Bhardwaj2009) and assuming the solution as
where b 0 is the initial beam width of the scattered wave, E S0 (r,z) and E S1 (r,z) are the slowly varying complex function of r and z, and the coefficients α 0s, etc. functions same as α 00 etc. functions in the previous section. We get the equation of the spot size of scattered wave as (Sharma et al., Reference Sharma, Sharma, Rajput and Bhardwaj2009)
with
where R dS = k S0b 02 is the diffraction length of the scattered radiation.
The expressions for B′ and b0 may be obtained on applying suitable boundary conditions E S = E S0 exp (ik S0z) + E S1 exp (−ik S1z) = 0 at z = z c; here z c is the point at which the amplitude of the scattered wave is zero. This immediately yields (Sharma et al., Reference Sharma, Sharma, Rajput and Bhardwaj2009)
![\eqalign{& B^{\prime} = - \displaystyle{1 \over 2}\displaystyle{{{\rm \omega} _p^2 } \over {c^2 }}\displaystyle{{{\rm \omega} _S } \over {{\rm \omega} _0 }}\displaystyle{{n_0 } \over {N_{00} }}\displaystyle{{E_{00}\, f_S \left({z_c } \right)} \over {\,f\left({z_c } \right)\,f_0 \left({z_c } \right)}}\cr &\quad \displaystyle{{\left({1 + \displaystyle{{{\rm \alpha} _{0i} r^2 } \over {a^2 f^2 }} + \displaystyle{{{\rm \alpha} _{2i} r^4 } \over {a^4 f^2 }}} \right)^{1/2} \left({1 + \displaystyle{{{\rm \alpha} _{00} r^2 } \over {r_0^2\, f_0^2 }} + \displaystyle{{{\rm \alpha} _{02} r^4 } \over {r_0^4\, f_0^4 }}} \right)^{1/2} } \over {\left({1 + \displaystyle{{{\rm \alpha} _{0s} r^2 } \over {b_0^2\, f_s^2 }} + \displaystyle{{{\rm \alpha} _{2s} r^4 } \over {b_0^4\, f_s^4 }}} \right)^{1/2} }}. \cr & \quad \displaystyle{{\exp \left({ - k_i z_c } \right)} \over {\left[{k_{S1}^2 - k_{S0}^2 - \displaystyle{{{\rm \omega} _p^2 } \over {c^2 }}\left({1 - \displaystyle{{N_{0e} } \over {N_{00} }}} \right)} \right]}}\cr &\quad \displaystyle{{\exp \left[{ - i\left({k_{S1} z_c + k_0 S_0 } \right)} \right]} \over {\exp \left[{i\left({k_{S0} S_s+k_{S0} z_c } \right)} \right]}}\comma\, }](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461100084X_eqn32.gif?pub-status=live)
With condition 
here 
and ks1 and ωs satisfy the matching conditions ωS = ω0 − ω k S1 = k 0 − k. The reflectivity is defined as the ratio of scattered flux and incident flux, R = (| E S |2 / | E 00 |2). By following (Sharma et al., Reference Sharma, Sharma, Rajput and Bhardwaj2009), we get
![\eqalign{E_S E_S^{\ast} & = E_{S0} E_{S0}^{\,\ast} + E_{S0} E_{S1}^{\ast} \exp \left[{i\left({k_{S0} + k_{S1} } \right)z} \right]\cr & \quad + E_{S1} E_{S0}^{\,\ast} \exp \left[{ - i\left({k_{S0} + k_{S1} } \right)z} \right]+ E_{S1} E_{S1}^{\,\ast}\comma \; }](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461100084X_eqnU3.gif?pub-status=live){kind=small}
and
![\eqalign{&R = \displaystyle{1 \over 4}\left({\displaystyle{{{\rm \omega} _p^2 } \over {c^2 }}} \right)^2 \left({\displaystyle{{{\rm \omega} _s } \over {{\rm \omega} _0 }}} \right)^2 \left({\displaystyle{{n_0 } \over {N_{00} }}} \right)^2\cr &\quad \displaystyle{1 \over {\left[{k_{s1}^2 - k_{s0}^2 - \displaystyle{{{\rm \omega} _p^2 } \over {c^2 }}\left({1 - \displaystyle{{n_0 } \over {N_{00} }}} \right)} \right]^2 }}\cr & \left[\matrix{\displaystyle{{\,f_S^2 \left({z_c } \right)} \over {\,f^2 \left({z_c } \right)f_0^2 \left({z_c } \right)}}\displaystyle{1 \over {\,f_S^2 }}\exp \left({ - 2k_i z_c - \displaystyle{{r^2 } \over {b_0^2 \,f_s^2 }}} \right)\hfill \cr + \displaystyle{1 \over {\,f^2 f_0 ^2 }}\exp \left({ - \displaystyle{{r^2 } \over {a^2 f^2 }} - \displaystyle{{r^2 } \over {b_0^2\, f_0^2 }} - 2k_i z} \right)\hfill \cr + \displaystyle{1 \over 2}\displaystyle{1 \over {\,ff_0\, f_s }}\displaystyle{{\,f_s \left({z_c } \right)} \over {\,f\left({z_c } \right)f_0 \left({z_c } \right)}}\exp \left({ - \displaystyle{{r^2 } \over {2b_0^2\, f_s^2 }} - \displaystyle{{r^2 } \over {2a^2 f^2 }} - \displaystyle{{r^2 } \over {2r_0^2\, f_0^2 }}} \right)\hfill \cr .\exp \big\{{ - k_i \left({z+z_c } \right)} \big\}\cos \big\{{\left({k_{S0} + k_{S1} } \right)\left({z - z_c } \right)} \big\}\hfill \cr \times \displaystyle{{\left({1 + \displaystyle{{{\rm \alpha} _{0i} r^2 } \over {a^2 f^2 }} + \displaystyle{{{\rm \alpha} _{2i} r^4 } \over {a^4 f^2 }}} \right)^{1/2} \left({1 + \displaystyle{{{\rm \alpha} _{00} r^2 } \over {r_0^2\, f_0^2 }} + \displaystyle{{{\rm \alpha} _{02} r^4 } \over {r_0^4\, f_0^4 }}} \right)^{1/2} } \over {\left({1 + \displaystyle{{{\rm \alpha} _{0s} r^2 } \over {b_0^2\, f_s^2 }} + \displaystyle{{{\rm \alpha} _{2s} r^4 } \over {b_0^4\, f_s^4 }}} \right)^{1/2} }} \hfill} \right].}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary-alt:20160626080114-21987-mediumThumb-S026303461100084X_eqn33.jpg?pub-status=live)
SBS reflectivity is numerically calculated by using the above set of equations.
4. DISCUSSIONS
The propagation of high power laser beam has been considered in the presence of ponderomotive nonlinearity. The density of the plasma varies due to the ponderomotive force and this force is also responsible for the lowering of the channel density, therefore the refractive index increases and the laser gets focused in the plasma. Eqs. (4) and (5) describe the intensity profile of laser beam in plasma along the radial direction when the ponderomotive nonlinearity is operative. The intensity profile of the laser beam depends on the beam width f 0, and the coefficients (α 00 and α 02) of r 2 and r 4 in the non-paraxial region. Eq. (6) determines the focusing/defocusing of laser beam along the distance of propagation in plasma. In Eq. (6), the first term is responsible for diffraction, while the second and third terms (nonlinear terms), on the right-hand side of the equation are responsible for the converging behavior of the beam during propagation in plasma. These three terms describe the filament formation and the laser beam propagation in plasma. Numerical evaluation of Eqs. (4) and (5) has been performed by using the typical laser beam parameters: the vacuum wavelength of the laser beam (λ = 1064 nm), the initial radius of the laser beam (15 µm), laser power flux (1016 W/cm2) at plasma density, n/n cr = 0.11 and v th = 0.1c. For initial wave front of the beam, the initial conditions for f 0 are f 0 = 1 and df 0/dz at z = 0 and S 00 and S 02 = 0 at z = 0. The coupled equations have been solved with the help of Eqs (6)–(9) for an initial plane wave front of the beam and the numerical results are presented in the form of Figure 1. Figure 1a depicts the variation in laser beam intensity with normalized distance and radial distance, when the paraxial approximation is taken into consideration (by substituting α00 and α02 = 0 in Eq. (2)). But when the values of α00 and α02 are taken into account, the coupled equations have been solved and numerical results are presented in the form of Figure 1b. Figure 1b shows the variation of the laser beam intensity with normalized distance and radial distance including the extended-paraxial contribution. It is obvious from the figure that the beam has spitted profile and in paraxial region the intensity of laser beams is maximum at r = 0 along the distance of propagation as α00 = α02 = 0. While in extended-paraxial region the laser intensity becomes minimum at r = 0, and maximum at r =± 0.45, as also verified analytically by Eq. (4). In Figure 2, a comparison of beam width parameter has been done for both the cases paraxial and modified paraxial. It can clearly be observed from Figure 2 that focusing becomes faster in extended-paraxial case in comparison to paraxial case due to the participation of off-axis parts (α00 ≠ α02 ≠ 0).
Fig. 1. (Color online) Variation of laser beam intensity with normalized distance and radial distance (a) in paraxial case (α00 = α02 = 0) (b) in extended-paraxial case (α00 = α02 = 0).
Fig. 2. (Color online) Variation in laser beam width parameter with normalized distance, where red dashed line is for on axis (paraxial) case i.e. (α00 = α02 = 0) and solid black line is for off-axial (extended paraxial) contribution i.e. (α00 ≠ α02 ≠ 0).
When this laser beam propagates through plasma, the motion of electron will be modified according to the nonlinearity present in the plasma and will give rise to changes in the dispersion of the laser beam and nonlinear current density. Nonlinear interaction of seed IAW with the laser beam leads to its excitation. It is evident from the figure that IAW gets excited due to nonlinear coupling with high-power laser beam because of ponderomotive nonlinearity. We have solved Eq. (14) numerically with the help of all set of Eq. (16) to obtain the amplitude of the density perturbation at finite z. The results are displayed in Figure 3, for typical laser parameters as mentioned earlier. It is evident from the figure that the IAW gets excited due to nonlinear coupling with high power laser beam because of the ponderomotive nonlinearity. This coupling is so strong that the initial ion wave becomes highly localized as shown in Figure 3; it depicts that the IAW is also having the spitted profile with minimum power on the axis.
Fig. 3. (Color online) Variation of ion acoustic wave density with normalized distance and radial distance in extended — paraxial case (α0i = α2i = 0).
Eq. (28) expresses the beam width parameter of the scattered beam and Eq. (33) gives the reflectivity has been derived including off-axial coefficients. In order to observe the reflectivity against the distance of propagation, we have solved Eq. (33) numerically and the results are presented in the form of Figure 4, which shows the variation of the reflectivity with normalized distance with and without the contribution of the coefficients α00 and α02. Figure 4 explicitly illustrates the comparison of reflectivity in the off-axis (α00 ≠ α02 ≠ 0) and on-axis cases (α00 = α02 = 0) of the laser beam. In Figure 4, the blue dotted line shows normalized reflectivity when restriction on the laser beam is relaxed while solid black line shows the same with restricted laser beam profile. It is observed that the reflectivity is about an order of magnitude lower with respect to the paraxial case and, the blue dotted lines come towards the left-hand side of the solid black line, it depicts that non-paraxial rays reflects earlier than the paraxial rays This is due to the fact that, in the modified paraxial case focusing becomes faster and hence the scattered wave also reflects earlier with respect to the paraxial case as shown in the blue dotted line.
Fig. 4. (Color online) Variation in normalized reflectivity with normalized distance, where black solid line is for on axis (paraxial) case when (α01= α02 = 0) (α0i= α2i = 0). (α0s = α2s = 0) blue dotted line is for off-axial (extended paraxial) contribution when (α01 ≠ α02 ≠ 0). (α0i ≠ α2i ≠ 0). (α0s ≠ α2s ≠ 0).
5. CONCLUSION
In this work, it is observed that the spitted profile of the laser beam modify the process of excitation ion acoustic wave. This modified profile of the laser beam affects the nonlinear coupling between the laser beam and IAW. Further, it is investigated that the SBS is also influenced by this coupling process, as the reflectivity depends on the density of IAW. Therefore, the reflectivity of SBS has been compared with and without contribution of off-axial rays. A considerable change is found in the level of SBS reflectivity in modified-paraxial case in comparison to the paraxial case. It is expected that these results will contribute to make smaller the discrepancy between theoretical prediction and experimental results.
ACKNOWLEDGMENT
This work was partially supported by MAPCOST, Bhopal India and DST, New Delhi India.
