Introduction
In last two decades, the terahertz (THz) radiation in the frequency region 0.1–30 THz has attracted great interest and has become an important area of research in both fundamental and applied sciences. THz radiation has a wide range of applications due to its non-ionizing behavior. Also, it can penetrate in a wide variety of non-conducting materials (Dragoman and Dragoman, Reference Dragoman and Dragoman2004). THz radiation sources have a number of applications in the field of spectroscopy (Beard et al., Reference Beard, Turner and Schmuttenmaer2002), communication (Bass et al., Reference Bass, Franken, Ward and Weinreich1962), remote sensing (Ferguson et al., Reference Ferguson, Wang, Gray, Abbott and Zhang2002), THz time-domain spectroscopy (Shen, Reference Shen2011), sub-millimeter astronomy (Federici et al., Reference Federici, Schulkin, Huang, Gary, Barat, Oliveira and Zimdars2005), materials characterization (Ferguson and Zhang, Reference Ferguson and Zhang2002), security screening (Federici et al., Reference Federici, Schulkin, Huang, Gary, Barat, Oliveira and Zimdars2005), tomography (Hu and Nuss, Reference Hu and Nuss1995), topography (Wang et al., Reference Wang, Ferguson, Abbott and Zhang2003), and medical diagnostic (Globus et al., Reference Globus, Woolard, Bykhovskaia, Gelmont, Werbos and Samuels2003; Zeitler et al., Reference Zeitler, Taday, Newnham, Pepper, Gordon and Rades2007). Due to the non-availability of compact and high-power THz radiation sources, the researchers are continuously working toward finding a promising way to generate and tune THz radiation of high amplitude, power, and efficiency with reasonable size.
A variety of schemes are proposed to generate THz from solid-state materials (e.g. electro-optic crystals) such as GaAs, LaTio3, ZnSe, GaP, InP, and LiNbO3 (Kawase et al., Reference Kawase, Sato, Taniuchi and Ito1996; Kadow et al., Reference Kadow, Jackson, Gossard, Matsuura and Blake2000; Sakai, Reference Sakai2005). The low damage threshold of these materials, low conversions efficiency, and narrow band width make it difficult to generate high-power, highly efficient, and tunable THz sources using them. Due to these disadvantages, in last few years, a lot of investigations have been carried out to introduce new schemes for THz generation. Plasma, being a broken medium, has no damage threshold and can handle very high-power laser beam. Hence, several laser–plasma interactions-based schemes (experimentally and theoretically) have been proposed by researchers for high-power THz radiation sources (Hamster et al., Reference Hamster, Sullivan, Gordon, White and Falcone1993, Reference Hamster, Sullivan, Gordon and Falcone1994; Cook and Hochstrasser, Reference Cook and Hochstrasser2000; Löffler et al., Reference Löffler, Jacob and Roskos2000; Carr et al., Reference Carr, Martin, Mckinney, Jordan, Neil and Williams2002; Dai et al., Reference Dai, Xie and Zhang2006; Biedron et al., Reference Biedron, Lewellen, Milton, Gopalsami, Schneider, Skubal, Li, Virgo, Gallerano and Doria2007; Liu et al., Reference Liu, Houard, Prade, Akturk, Mysyrowicz and Tikhonchuk2007; Houard et al., Reference Houard, Liu, Prade, Tikhonchuk and Mysyrowicz2008; Kim et al., Reference Kim, Taylor, Glownia and Rodriguez2008; Liu and Tripathi, Reference Liu and Tripathi2009; Malik et al., Reference Malik, Malik and Kawata2010, Reference Malik, Uma and Kumar2017; Tripathi et al., Reference Tripathi, Bhasin, Uma and Tripathi2010; Malik and Malik, Reference Malik and Malik2012; Singh et al., Reference Singh, Mahmoud and Sharma2012; Nafil et al., Reference Nafil, Singh, Al-Janabi and Sharma2013; Mondal et al., Reference Mondal, Hafez, Ropagnol and Ozaki2017; Wang et al., Reference Wang, Ju, Liu, Li, Xu and Leang Chin2017).
THz generation using laser filamentation, self-focusing, cross-focusing, and photoionization in plasma using highly intense ultra-short picosecond or a femtosecond range laser pulses have been performed by several researchers (Carr et al., Reference Carr, Martin, Mckinney, Jordan, Neil and Williams2002; Dai et al., Reference Dai, Xie and Zhang2006; Biedron et al., Reference Biedron, Lewellen, Milton, Gopalsami, Schneider, Skubal, Li, Virgo, Gallerano and Doria2007; Houard et al., Reference Houard, Liu, Prade, Tikhonchuk and Mysyrowicz2008; Kim et al., Reference Kim, Taylor, Glownia and Rodriguez2008). Chen et al. (Reference Chen, Yamaguchi, Wang and Zhang2007) have reported that THz generation experiment in laser produced plasma from a series of noble gases. They have shown that the THz efficiency increases with decreasing ionization potential. Hamster et al. (Reference Hamster, Sullivan, Gordon, White and Falcone1993) experimentally demonstrated THz radiation from short-pulse laser beam focused on gas and solid targets. They also examined THz radiation in laser-induced plasma channel where ponderomotive force drives THz radiation (Hamster et al., Reference Hamster, Sullivan, Gordon and Falcone1994). Babushkin et al. have studied numerically (Babushkin et al., Reference Babushkin, Skupin and Herrmann2010b) and experimentally (Babushkin et al., Reference Babushkin, Kuehn, Köhler, Skupin, Bergé, Reimann, Woerner, Herrmann and Elsaesser2010a) the THz radiation in air and noble gas by two color lasers in an ionizing plasma using 0.8 and 1.6 µm laser of 50 fs duration.
The analytical investigation of the THz radiation generation by non-linear mixing of two laser beams in plasma having their frequency differences in THz region have been studied by many researchers in the last few years (Bhasin and Tripathi, Reference Bhasin and Tripathi2009; Liu and Tripathi, Reference Liu and Tripathi2009; Pathak et al., Reference Pathak, Dahiya and Tripathi2009; Kumar et al., Reference Kumar, Bhasin and Tripathi2010, Reference Kumar, Lee, Hee Park, Uk Jeong and Vinokurov2017; Malik et al., Reference Malik, Malik and Kawata2010, Reference Malik, Uma and Kumar2017; Sharma et al., Reference Sharma, Monika, Sharma, Chauhan and Ji2010; Malik and Malik, Reference Malik and Malik2011, Reference Malik and Malik2013; Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013, Reference Varshney, Sajal, Baliyan, Sharma, Chauhan and Kumar2015a, Reference Varshney, Sajal, Singh, Kumar and Sharma2015b, Reference Varshney, Sajal, Upadhyay, Chakera and Kumar2017; Malik, Reference Malik2014, Reference Malik2015; Sharma and Singh, Reference Sharma and Singh2014; Singh and Sharma, Reference Singh and Sharma2014; Varshnety et al., Reference Varshnety, Sajal, Chauhan, Kumar and Sharma2014; Bakhtiari et al., Reference Bakhtiari, Golmohammady, Yousefi, Kashani and Ghafary2015a, Reference Bakhtiari, Yousefi, Golmohammady, Jazayeri and Ghafary2015b, Reference Bakhtiari, Esmaeilzadeh and Ghafary2017; Gill et al., Reference Gill, Singh and Malik2017; Rawat et al., Reference Rawat, Rawat, Gaur and Purohit2017; Singh et al., Reference Singh, Singh, Rajouria and Sharma2017). Cho et al. (Reference Cho, Kim, Suk, Ersfeld, Jaroszynski and Hur2015) have demonstrated a new mechanism for THz generation based on laser–plasma interaction. They have shown that a monochromatic THz radiation with a field strength of 
$\sim \!\!10^7{\kern 1pt} {\rm V/m}$ can be produced by two counter propagating short laser pulse in weakly magnetized plasma. THz radiation by laser–plasma interaction in rippled plasma density has been studied by many researchers. Its role in the generation process has been examined and discussed in detail (Bhasin and Tripathi, Reference Bhasin and Tripathi2009; Pathak et al., Reference Pathak, Dahiya and Tripathi2009; Tripathi et al., Reference Tripathi, Bhasin, Uma and Tripathi2010; Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2013, Reference Varshney, Sajal, Upadhyay, Chakera and Kumar2017). Antonsen Jr et al. (Reference Antonsen, Palastro and Milchberg2007) have analytically studied phase-matched THz radiation generation by the ponderomotive force of a laser pulse with the employment of a corrugated plasma channel. In another analytical study, Bhasin and Tripathi (Reference Bhasin and Tripathi2009) have obtained THz radiation with an efficiency of 10−4 by the optical rectification of an x-mode picosecond laser pulse in a rippled density magnetized plasma. Their model was further improved by Varshney et al. (Reference Varshney, Sajal, Singh, Kumar and Sharma2013) by including the effects of the static magnetic field on ponderomotive force.
Various laser profiles, for example, Gaussian (Bhasin and Tripathi, Reference Bhasin and Tripathi2009; Malik et al., Reference Malik, Malik and Kawata2010; Singh and Sharma, Reference Singh and Sharma2014), triangular (Malik et al., Reference Malik, Malik and Stroth2011; Varshney et al., Reference Varshney, Sajal, Baliyan, Sharma, Chauhan and Kumar2015a), cosh-Gaussian (Singh et al., Reference Singh, Singh and Sharma2013; Mann et al., Reference Mann, Sajal, Varshney and Sharma2017; Varshney et al., Reference Varshney, Sajal, Upadhyay, Chakera and Kumar2017), super-Gaussian (Malik et al., Reference Malik, Malik and Kawata2010; Malik and Malik, Reference Malik and Malik2012; Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2015b), and flat-top (Bakhtiari et al., Reference Bakhtiari, Esmaeilzadeh and Ghafary2017) have been used to generate strong and tunable THz radiation because laser beams with different intensity profiles behave differently in plasmas. For example, Malik et al. have utilized the super-Gaussian (Malik and Malik, Reference Malik and Malik2012), Gaussian (Malik et al., Reference Malik, Malik and Stroth2012), and spatial triangular (Malik et al., Reference Malik, Malik and Stroth2011) profiles of beating lasers in a periodic density rippled plasma for THz generation and obtained a maximum efficiency of about 10−2 for the laser intensity of 
$10^{14}{\kern 1pt} {\rm W/c}{\rm m}^{\rm 2}$. They have also shown that stronger THz radiation can be produced with the help of two spatial super-Gaussian lasers of higher index and smaller beam width (Malik and Malik, Reference Malik and Malik2012). Singh et al. (Reference Singh, Singh and Sharma2013) have obtained THz radiation with an efficiency of 10−5 by beating of two cosh-Gaussian laser beams in spatially periodic density plasma. This model has been further improved by Varshney et al. (Reference Varshney, Sajal, Upadhyay, Chakera and Kumar2017) by including the effects of the static magnetic field in the plasma where they have shown three-order higher efficiency.
In most of the THz radiation generation schemes mentioned earlier, the electron-neutral collisions in plasma has not been taken into account as it leads to drastic reduction in the emitted THz power and efficiency. Also, the joint effects of the collisions and the magnetic fields have not been considered. Singh and Malik (Reference Singh and Malik2015) have considered the effects of collisional plasma for THz radiation generation by mixing two super-Gaussian laser beams. They have shown that electron-neutral collision and larger beam width lead to significant change in THz amplitude. But when super-Gaussian laser is used in plasma, the efficiency of mechanism remains much higher than the case of Gaussian lasers. They have also studied the effect of magnetic field and demonstrated 6% efficiency (Singh and Malik, Reference Singh and Malik2014). Recently, generation of THz radiation by hollow-Gaussian laser beams in collisional plasmas has been studied by Bakhtiari et al. (Reference Bakhtiari, Golmohammady, Yousefi, Kashani and Ghafary2015a) where they observed the efficiency of THz radiation is very small, which is due to the collisional effect. By considering the interaction of two flat-topped laser profiles, Bakhtiari et al. (Reference Bakhtiari, Esmaeilzadeh and Ghafary2017) demonstrated an efficiency of THz generation of 8.3% in a collisional plasma.
In this work, we study THz radiation generation by beating of two coaxial cosh-Gaussian laser beams propagating in rippled density magnetized plasma in the presence of applied axial static magnetic field. The cosh-Gaussian beams (decentered Gaussian beams) have raised considerable interest in recent times on account of their spatial profile. These beams control higher efficient power with flat-top beam shape and hollow-Gaussian lasers beam in comparison with that of a Gaussian beam. Contrary to the case of two Gaussian spatial profile lasers, THz radiation can be focused at a desired position by choosing suitable decentered parameters of cosh-Gaussian lasers (Varshney et al., Reference Varshney, Sajal, Upadhyay, Chakera and Kumar2017). We show that in magnetized plasma, if the effect of electron-neutral collisions is taken into account, THz radiation enhances significantly in terms of the amplitude and efficiency. In a specific parameter domain, the joint effect of the magnetic field and electron-neutral collisions causes enhancement of THz amplitude and efficiency. Optimizing the plasma and laser beam parameters and considering the mutual effect, we obtain the efficiency of THz generation up to 15%, which is considerably high relative to the efficiency obtained in the previously studied schemes. In “Calculation of nonlinear current density, THz radiation field amplitude and efficiency” section, we develop the analytical model of THz radiation in collisional and magnetized plasma, and equations for the emitted THz field amplitude and efficiency are then derived. The results of the numerical study are presented and discussed in “Analytical result and discussion” section. Finally, “Conclusions” section contains conclusion.
Calculation of non-linear current density, THz radiation field amplitude, and efficiency
We consider two circular symmetric cosh-Gaussian laser beams with different frequencies (ω1 and ω2) and wave numbers (
$\vec k_1$ and 
$\vec k_2$) co-propagating along z-axis in the collisional plasma (electron-neutral collisions). A static magnetic field B 0 is applied along the direction of wave propagation. The profile of laser electric fields is given as
$$\vec E_j = (\hat xE_{0jx} + \hat yE_{0jy})\cosh \left( {\displaystyle{{rb} \over {r_0}}} \right)e^{ - {{y^2} / {r_0^2}}} e^{ - i({\rm \omega} _jt - k_jz)},$$where
$$E_{0jx} = E_{0jy} = E_{0j}.$$ Here, 
$k_j = ({\rm \omega} _j/c)\{ {1 - ({\rm \omega} _{\rm p}^2 /{\rm \omega} _j(\Omega _j - {\rm \omega} _{\rm c}))} \}^{1/2}$, j = 1, 2 for two lasers and Ωj = ωj − iυen. Here, ωp = (4πn 0ee 2/m)1/2 is the plasma frequency (in CGS), cyclotron frequency ωc = eB 0/mc (in CGS), υen is the collisional frequency, r 0 is the initial beam width, b is the decentered parameter, e is the electronic charge, and m is the electronic mass. The electric field profile given by Eq. (1) is plotted in Figure 1. One can notice that as decentered parameter of the cosh-Gaussian laser beam changes from b = 0 to 5, the profile changes its shape in the following sequences: (i) Gaussian (b = 0), (ii) flat-top (b = 1.45), (iii) ring shape (b = 2), and (iv) hollow-Gaussian (b = 5).
Fig. 1. Normalized cosh-Gaussian laser field amplitude E j/E 0j as a function of transverse distance r for decentered parameters 0 <b ≤ 5.
The plasma has a periodic density ripple given by n = n 0 + n′, n′ = n α0e iαz, where n α0 is the amplitude of ripple and α is the repetition factor for density ripples. This density ripple may be created using various techniques, for example, by machining pre-pulse and a patterned mask, where plasma gas jet is exposed to an ultrahigh-intensity laser pulse through a patterned mask of periodic opacity. Hydrodynamics expansions, in the irradiated regions exposed to higher intensity part of laser, are created due to heating by the laser pulse and plasma density drops in this region. Thus, a masked laser beam can be utilized to pre-form the spatially periodic ripple density structure in the plasma. Here, one can control ripple parameters (n α0 and α) by changing the size of the masks (Pai et al., Reference Pai, Huang, Kuo, Lin, Wang, Chen, Lee and Lin2005). Taking in to account the electron-neutral collisions, the equation of motion for laser beams can be written as (Chen and Trivelpiece, Reference Chen and Trivelpiece1976):
$$m\displaystyle{{d\,{\vec v}_j} \over {dt}} = - e\vec E_j - e\,(\vec v_j \times \vec B_j) - m{\rm \upsilon} _{en}\vec v_j.$$ The last term in Eq. (3) represents the collisional force. Plasma electron oscillates under the influence of electric field of beating lasers and attains oscillating velocities having 
$\hat x$ and 
$\hat y$ components, given by
$$v_{\,jx} = \displaystyle{{eE_{\,jx}\Omega _j} \over {mi(\Omega _j^2 - {\rm \omega} _{\rm c}^2 )}} - \displaystyle{{eE_{\,jy}{\rm \omega} _{\rm c}} \over {m(\Omega _j^2 - {\rm \omega} _{\rm c}^2 )}},$$
$$v_{\,jy} = \displaystyle{{eE_{\,jy}\Omega _j} \over {mi(\Omega _j^2 - {\rm \omega} _{\rm c}^2 )}} + \displaystyle{{eE_{\,jx}{\rm \omega} _{\rm c}} \over {m(\Omega _j^2 - {\rm \omega} _{\rm c}^2 )}}.$$ Two lasers beating at frequency ω = ω1 − ω2 and wave vector 
${\vec k}{^\prime} = \vec k_1 - \vec k_2$ create a non-linear ponderomotive force 
$\vec F_{\rm p}^{{\rm NL}} $ on plasma electrons, which is given by:
$$\vec F_{\rm p}^{{\rm NL}} = - \displaystyle{{m\nabla {\vec v}_1.\vec v_2{^\ast}} \over 2}.$$The non-linear ponderomotive force is evaluated using Eq. (4) and becomes
$$\eqalign{ \vec F_{\rm p}^{\,{\rm NL}} & = \displaystyle{{e^2} \over {m(\Omega _1 - {\rm \omega} _{\rm c})(\Omega _2^{^\ast} - {\rm \omega} _{\rm c})}} \cr & \quad \nabla \left[ {{\cosh} ^2\left( {\displaystyle{{rb} \over {r_0}}} \right) \times \exp \left( { - \displaystyle{{2r^2} \over {r_0^2}}} \right)} \right]\exp \left( { - i\,({\rm \omega} \,t - {k}^{\prime}z)} \right).} $$This non-linear ponderomotive force causes perturbations in the density of plasma (n = n L + n NL) having linear component and non-linear component. These perturbations generate space charge potentials that lead to the linear density perturbation. The non-linear density perturbation is due to the non-linear ponderomotive force. This non-linear force imparts non-linear oscillatory velocity to the electrons, which is calculated by the equation of motion:
$$m\displaystyle{{\partial {\vec v}_{{\rm NL}}} \over {\partial t}} = F_{\rm p}^{{\rm NL}} - \displaystyle{e \over c}(\vec v^{\,{\rm NL}} \times \vec B_0) - m{\rm \upsilon} _{{\rm en}}\vec v^{\,{\rm NL}}.$$Here, we have taken into account only electron-neutral collisions. On solving Eq. (7), we obtain the value of non-linear velocity component as follows:
$$v_x^{{\rm NL}} = \displaystyle{{ - i{\rm \omega} _{\rm c}F_{{\rm p}y}^{{\rm NL}} + \Omega F_{{\rm p}x}^{{\rm NL}}} \over {m\,i\,(\Omega ^2 - {\rm \omega} _{\rm c}^2 )}},$$
$$v_y^{{\rm NL}} = \displaystyle{{i{\rm \omega} _{\rm c}F_{{\rm p}x}^{{\rm NL}} + \Omega F_{{\rm p}y}^{{\rm NL}}} \over {m\,i\,(\Omega ^2 - {\rm \omega} _{\rm c}^2 )}}.$$ This oscillatory velocity couples with preformed density ripple n α0e iαz and excites a non-linear current density at 
$({\rm \omega}, \,\vec k_1 - \vec k_2 + {\rm \vec \alpha} )$, which can be written as
$$\vec J^{\,{\,\rm NL}} = - \displaystyle{1 \over 2}n_{{\rm \alpha} 0}e\vec v_{}^{\,{\rm NL}} e^{i{\rm \alpha} z}.$$ The above equation shows that a non-linear transverse current is formed. This current may lead to radiation at different frequencies ω = ω1 − ω2 and wave numbers 
$\vec k( = \vec k_1 - \vec k_2 + {\rm \vec \alpha} )$. The value of ω and k may be chosen such that the generated radiation lies in the THz region. Using Maxwell's equations, the wave equation governing the propagation of THz radiation in axially magnetized plasma can be written as:
$$\nabla ^2\vec E_{{\rm THz}} - {\vec{ \,\nabla}} ({\vec{ \,\nabla}}. \,\vec E_{{\rm THz}}) + \displaystyle{{{\rm \omega} ^2} \over {c^2}}({ {\bar {\bar \varepsilon}}} \,\vec E_{{\rm THz}}) = - \displaystyle{{4{\rm \pi} i{\rm \omega}} \over {c^2}}\vec J^{{\,\,\rm NL}},$$
where, 
${ {\bar {\bar \varepsilon}}} $ is the plasma permittivity tensor at ω and its components are 
${\rm \varepsilon} _{xx} = {\rm \varepsilon} _{yy} = \left[ {1 - ({\rm \omega} _{\rm p}^2 \Omega /{\rm \omega} (\Omega ^2 - {\rm \omega} _{\rm c}^2 ))} \right]$,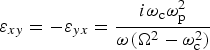 
${\rm \varepsilon} _{xy} = - {\rm \varepsilon} _{yx} = \displaystyle{{i{\rm \omega} _{\rm c}{\rm \omega} _{\rm p}^2} \over {{\rm \omega} (\Omega ^2 - {\rm \omega} _{\rm c}^2 )}}$, 
${\rm \varepsilon} _{zz} = \left[ {1 - ({\rm \omega} _{\rm p}^2 /{\rm \omega} \,\Omega )} \right]$, and εxz = εyz = εzx = εzy = 0. We wish to emphasize here that the transverse components of non-linear current density are the source of THz radiation generation. We can separate out the transverse components of Eq. (10) as follows:
$$\eqalign{ & \nabla ^2E_{x{\rm THz}} - \displaystyle{\partial \over {\partial x}}(\!{\vec {\, \nabla}}. \,\vec E_{{\rm THz}}) + \displaystyle{{{\rm \omega} ^2} \over {{\rm c}^2}}(\varepsilon _{xx}\,E_{x{\rm THz}} + \varepsilon _{xy}E_{y{\rm THz}}) \cr & \quad = - \displaystyle{{4{\rm \pi} i{\rm \omega}} \over {{\rm c}^2}}J_x^{{\rm NL}}}$$and
$$\eqalign{ & \nabla ^2E_{y{\rm THz}} - \displaystyle{\partial \over {\partial y}}(\!{\vec {\, \nabla}}. \,\vec E_{{\rm THz}}) + \displaystyle{{{\rm \omega} ^2} \over {c^2}}({\rm \varepsilon} _{yx}\,E_{x{\rm THz}} + \varepsilon _{yy}E_{y{\rm THz}}) \cr & \quad = - \displaystyle{{4{\rm \pi} i{\rm \omega}} \over {c^2}}J_y^{{\rm NL}}.} $$We multiply Eq. (12) by i and subtract it from Eq. (11) and also use Eq. (2) to obtain
$$\eqalign{\nabla ^2E_{x{\rm THz}} - & \displaystyle{1 \over 2}\left[ {\left( {\displaystyle{\partial \over {\partial x}} - i\displaystyle{\partial \over {\partial y}}} \right)(\!{\vec {\, \nabla}}. \,{\vec E}_{{\rm THz}})} \right] + \displaystyle{{{\rm \omega} ^2} \over {c^2}}({\rm \varepsilon} _{xx} + i{\rm \varepsilon} _{xy})E_{x{\rm THz}} \cr & = - \displaystyle{{4{\rm \pi} i{\rm \omega}} \over {c^2}}(J_x^{{\rm NL}} - iJ_y^{{\rm NL}} ).}$$ Taking fast-phase variations in the electric field of THz radiation as 
$E_{x{\rm THz}} = E_{0{\kern 1pt} {\rm THz}}\exp \,\{ - i({\rm \omega} t - kz)\} $ and neglecting second-order perturbations of Eq. (13), we can write Eq. (13) as:
$$\eqalign{ & 2ik\displaystyle{\partial \over {\partial z}}E_{0{\kern 1pt} {\rm THz}} + \left( {\displaystyle{{{\rm \omega} ^2} \over {c^2}}({\rm \varepsilon} _{xx} + i{\rm \varepsilon} _{xy}) - k^2} \right)E_{0{\kern 1pt} {\rm THz}} \cr & \quad = \displaystyle{{4{\rm \pi} i{\rm \omega}} \over {c^2}}(J_x^{{\rm NL}} - iJ_y^{{\rm NL}} ).}$$The resonance condition of phase matching in the presence of periodic plasma density ripple demands that the second term on left-hand side of Eq. (14) is equal to zero. This leads to the dispersion relation of THz.
$$k^2 = \displaystyle{{{\rm \omega} ^2} \over {c^2}}({\rm \varepsilon} _{xx} + i{\rm \varepsilon} _{xy}) = \displaystyle{{{\rm \omega} ^2} \over {c^2}}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} (\Omega - {\rm \omega} _{\rm c})}}} \right).$$ This second term on left-hand side of Eq. (14) suggests that the maximum energy transfer from beating lasers to oscillating electron current leading to THz radiation will take place at resonance condition 
$\vec k = \vec k_1 - \vec k_2 + {\rm \alpha} $ and ω = ω1 − ω2 ≈ ωh. The periodicity of density ripples required for the fine tuning of maximum energy transfer is calculated utilizing Eq. (15) as follows:
$$\alpha = \displaystyle{{\rm \omega} \over c}\left \vert {{\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} (\Omega - {\rm \omega} _{\rm c})}}} \right)}^{1/2} - 1} \right \vert. $$On recombining Eqs. (8), (9), (14), and (16), we obtain the phase-matched THz wave amplitude:
$$\eqalign{ E_{0\,{\rm THz}} & = \displaystyle{{n_{{\rm \alpha 0}}} \over {n_0}}\displaystyle{{{\rm \omega} _{\rm p}^2 {\rm \omega} \,zeE_{01}E_{02}^{^\ast} \exp ( - 2r^2/r_0^2 )} \over {8mikc^2({\rm \omega} _{\rm c} - {\rm \omega} )(\Omega _1 - {\rm \omega} _{\rm c})(\Omega _2^{^\ast} - {\rm \omega} _{\rm c})}} \cr & \quad \left[ {\displaystyle{{ - 2r} \over {r_0^2}} + \displaystyle{{2b} \over {r_0}}\sinh \left( {\displaystyle{{2rb} \over {r_0}}} \right) + \displaystyle{{4r} \over {r_0^2}} \cosh \left( {\displaystyle{{2rb} \over {r_0}}} \right)} \right].} $$Normalizing Eq. (17), we obtain final expression of the normalized amplitude of THz wave as follows:
$$\eqalign{ \left\vert \displaystyle{E_{0{\rm THz}} \over E_{01}} \right \vert & = \displaystyle{n_{{\rm \alpha} 0} \over n_0} \displaystyle{{\rm \omega}^{\prime}\,{z}^{\prime} \left\vert {v}_{02}^{\prime \ast} \right\vert \exp (- 2{r}^{\prime 2}/r_0^{\prime 2}) \over 8{k}^{\prime}({\rm \omega}_{\rm c}^{\prime} - {\rm \omega}^{\prime})({\Omega}_1^{\prime} - {\rm \omega}_{\rm c}^{\prime})({\Omega}_2^{\prime \ast} - {\rm \omega}_{\rm c}^{\prime})} \cr & \left[ \displaystyle{ - 2{r}^{\prime} \over {r}_0^{\prime 2}} + \displaystyle{{2b} \over r_0^{\prime}} \sinh \left( \displaystyle{2{r}^{\prime}b \over r_0^{\prime}} \right) + \displaystyle{4r^{\prime} \over r_0^{\prime 2}} \cosh \left( \displaystyle{2{r}^{\prime}b \over r_0^{\prime}} \right) \right],} $$
where z′ = zωp/c, 
${\Omega} ^{\prime}_1 = \Omega _1/{\rm \omega} _{\rm p},\,\,{\Omega}_2^{\prime*} = \Omega _2^* /{\rm \omega} _{\rm p}$, 
${r}^{\prime}_0 = r_0{\rm \omega} _{\rm p}/c$, 
${\rm {\omega} ^{\prime}}_{\rm c} = {\rm \omega} _{\rm c}/{\rm \omega} _{\rm p}$, ω′ = ω/ωp, k′ = kc/ωp, and r′ = rωp/c.
The efficiency of the emitted THz radiation can be calculated by the ratio of the THz radiation energy and the incident laser energy. The average electromagnetic energy stored per unit volume in electric and magnetic fields are given by the relations (Rothwell and Cloud, Reference Rothwell and Cloud2008; Varshney et al., Reference Varshney, Sajal, Singh, Kumar and Sharma2015b).
$$\left\langle {W_{,_i}} \right\rangle = \displaystyle{1 \over {8{\rm \pi}}} {\rm \varepsilon} _0\displaystyle{\partial \over {\partial {\rm \omega} _i}}\left[ {{\rm \omega} _i\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _i^2}}} \right)} \right]\left\langle {{\left \vert {E_i} \right \vert} ^2} \right\rangle, $$
$$\,\left\langle {W_{B_i}} \right\rangle = \displaystyle{{k^2} \over {8{\rm \pi} {\rm \mu} _0{\rm \omega} _i}}\left\langle {{\left \vert {E_i} \right \vert} ^2} \right\rangle. $$The energy densities of the incident lasers (W pump) and emitted radiation (W THz) are as follows:
$$W_{{\rm pump}} = \displaystyle{{{\rm \varepsilon} _0{{r}^{\prime}}_0} \over 2}\left \vert {E_{01}} \right \vert ^2\sqrt {\displaystyle{{\rm \pi} \over 2}} \left\{ {1 + \exp \left[ {\displaystyle{{b^2} \over 2}} \right]} \right\},$$
$$\eqalign{W_{\rm THz} & = {\rm \varepsilon}_0 \left\vert E_{01} \right\vert^2 \left[\displaystyle{n_{{\rm \alpha} 0} \over n_0} \displaystyle{{\rm \omega}^{\prime}\,{z}^{\prime} \left\vert v_{02}^{\prime \ast} \right\vert \over 16k^{\prime}r_0^{\prime} ({\rm \omega}_{\rm c}^{\prime} - {\rm \omega}^{\prime})({\Omega}_1^{\prime} - {\rm \omega}_{\rm c}^{\prime})({\Omega}_2^{\prime \ast} - {\rm \omega}_{\rm c}^{\prime})} \right] \cr &\quad \left[ 1 + 2b\,e^{b^2/2} \sqrt{2{\rm \pi}} \,Erf\left(\displaystyle{b \over \sqrt{2}} \right) \right].}$$The normalized efficiency of THz radiation generation can be evaluated as follows:
$$\eqalign{\eta _{{\rm THz}} & = \displaystyle{{W_{{\rm THz}}} \over {W_{{\rm pump}}}} = \sqrt {\displaystyle{2 \over {\rm \pi}}} \displaystyle{{n_{{\rm \alpha 0}}} \over {n_0}}\displaystyle{{{\rm {\omega} ^{\prime}}\,{z}^{\prime}\left \vert {{v}_{02}^{\prime \ast}} \right \vert} \over {8{k}^{\prime}{r}_0^{\prime 2} ({{\rm {\omega} ^{\prime}}}_{\rm c} - {\rm {\omega} ^{\prime}})({{\Omega} ^{\prime}}_1 - {{\rm {\omega} ^{\prime}}}_{\rm c})({\Omega}_2^{\prime \ast} - {{\rm {\omega} ^{\prime}}}_{\rm c})}} \cr & \quad\left[ {\displaystyle{{1 + 2b\,e^{b^2/2}\sqrt {2{\rm \pi}} \,Erf\left( {b/\sqrt 2} \right)} \over {1 + \exp \left[ {b^2/2} \right]}}} \right].}$$Analytical result and discussion
The numerical calculations have been performed for a picosecond CO2 laser and the following laser–plasma parameters: wavelength 
${\rm \omega} _{\rm L} = 1.866 \times 10^{14} {\rm rad/s}$ (
${\rm \lambda} _{\rm L} = 10.1 {\rm \mu m}$), laser beam waist size 
$r_0 = 30 {\rm \mu m}$, laser intensity 
$I_{\rm L} = 1.20 \times 10^{15} {\rm W/c}{\rm m}^{\rm 2}$ (
$E_{\rm L} = 9.55 \times 10^8 {\rm V/cm}$), and plasma electron density n 0 = 7.561 × 1016 cm−3 (
${\rm \omega} _{\rm p} = 1.555 \times 10^{13} {\rm rad/s}$).
In this model, resonant condition for excitation of THz radiation in Eq. (16) is calculated. As earlier, we said that the density ripple with periodicity 2π/α is required to be present in the plasma. Hence, αc/ωp represents the normalized wave number corresponding to the density ripples. From Eq. (16), the normalized wave number of ripple density αc/ωp as a function of normalized collisional frequency υen/ωp for different values of THz frequency is plotted in Figure 2. We observe that when we increase the value of collisional frequency, the normalized periodicity of ripple required to efficiently generate the THz radiation at beat wave frequency ω/ωp = 1.0 decreases, whereas at higher value of beat wave frequency, the normalized periodicity of ripples required for efficient THz generation remains more or less constant. This implies that at higher beat wave frequency, the THz generation becomes less sensitive to ripple frequency. So, at a given beat wave frequency ω/ωp ≥ 2.0, one will obtain THz radiation for very large range of collision frequency, provided the ripple frequency is kept at an optimum value. At a lower beat wave frequency, efficient THz generation will be possible for a given combination of α and νen.
Fig. 2. Plot of the normalized ripple factor αc/ωp as a function of the normalized collisional frequency υen/ωp at different normalized terahertz frequency ω/ωp.
The normalized wave number of ripple density αc/ωp as a function of normalized cyclotron frequency ωc/ωp for different values of collisional frequency is shown in Figure 3. It is observed that the normalized ripple wave number required for THz generation increases with increasing magnetic field (i.e. ωc). The lower collisional frequency νen of plasma (i.e. a higher plasma temperature) requires higher ripple wave number. For the enhanced THz radiation generation, the wavenumber plays a crucial role so static axially magnetic field can be used to tune for strong THz radiation generation.
Fig. 3. Plot of the normalized ripple factor αc/ωp as a function of the normalized cyclotron frequency ωc/ωp at different normalized collisional frequency υen/ωp.
Now we study the combined effect of cosh-Gaussian laser beams and collisional frequency on THz radiation generation. In Figure 4, we have plotted the generated normalized THz amplitude as a function of normalized beat wave frequency (THz frequency). These plots are generated for two different values of normalized collisional frequency and four different values of decentered parameter b at normalized cyclotron frequency 
${\rm \omega} _{\rm c}/{\rm \omega} _{\rm p} = 0.3\,(B_0 = 264 {\rm kG})$. The peak of THz amplitude always comes at a resonance condition 
${\rm \omega} \approx ({\rm \omega} _{\rm c}^{\rm 2} + {\rm \omega} _{\rm p}^{\rm 2} )^{1/2}$ irrespective of the laser profile.
Fig. 4. Plot of the normalized terahertz amplitude ln(E THz/E 01) as a function of the normalized terahertz frequency ω/ωp at different normalized collisional frequency υen/ωp and decentered parameter b.
As shown in Figure 4, with the increase in the value of decentered parameter, the normalized THz amplitude increases and is two order higher for hollow-Gaussian beam (b = 5) as compared with Gaussian beam (b = 0) as the decentered parameter increases, the Gaussian beam peak initially becomes flat-top and then splits into two pulselets in space. This leads to enhanced ponderomotive non-linearity thereby leading to strong non-linear currents and strong THz radiation. Here, we also observe that the peak of normalized THz amplitude increases by few times when collision frequency goes down, that is, plasma is hotter. It is pertinent to mention here that the THz radiation amplitude shows a peak behavior for the magnetized plasma. Using these results, one can change the collision frequency of the plasma and/or magnetic field strength to obtain maximum THz radiation generation. The strength of the magnetic field can be easily tuned by changing the electric current in a solenoid. The collision frequency depends on the electron temperature T e through the relation υen = υ0(T e/T 0)s/2, where s is the collision parameter characterizing the type of collision and T 0 is the electron temperature (Sodha et al., Reference Sodha, Ghatak and Tripathi1974). Thus, by changing the electron temperature, one can tune the collision frequency.
The resonance condition for THz yield is predominantly controlled by magnetic field (ωc) for phase-matching condition of ω and by ripple frequency (α) for phase-matching condition of 
$\vec k$. For our values of ωc/ωp = 0.3 and αc/ωp = 0.3, we observe from Figure 4 that at normalized beat wave frequency ω/ωp = 11.8, that is, a THz frequency (υTHz = 11.8), we obtain a peak for every decentered parameter (b) and collision frequency. The amplitude of peak decreases and the full-width half-maxima (FWHM) increases with increasing the value of collisional frequency. The appearance of peak in the THz yield is due the resonance of beat wave frequency and plasma frequency under the effect of applied magnetic field (B 0) and density ripples. In Figure 5, we show the effect of normalized collisional frequency on normalized THz amplitude and FWHM of the peaks in Figure 4. At ω/ωp = 11.8, the normalized THz amplitude decreases with increasing the value of normalized collisional frequency, while the value of FWHM increase. This shows that to generate a shop peak of higher amplitude of THz, one needs lower collision frequency of plasma, that is, a warm plasma.
Fig. 5. Plot of the normalized terahertz amplitude E THz/E 01 and FWHM of terahertz wave as a function of the normalized terahertz frequency υen/ωp at normalized terahertz frequency ω/ωp = 11.8.
Now, we study the effect of decentered parameter (b) in the presence of a fixed magnetic field B 0 = ωcm/e and fixed ripple frequency on the shape and magnitude of generated THz field amplitude. Figure 6 shows the normalized THz amplitude as a function of beat wave frequency at different values of decentered parameter b. The cyclotron frequency ωc/ωp = 0.8 and normalized ripple factor αc/ωp = 0.3 have been kept at a constant value. It is seen that, with the increasing value of decentered parameter, the magnitude of emitted THz radiation field increases significantly. The change in magnitude is of three orders from a pure Gaussian beam to a hollow-Gaussian beam.
Fig. 6. Plot of the normalized terahertz amplitude ln(E THz/E 01) as a function of the normalized terahertz frequency ω/ωp at different decentered parameter b.
In Figure 7, the normalized THz field amplitude versus normalized beat wave frequency at different cyclotron frequency (i.e. magnetic field) and same decentered parameter have been plotted. As cyclotron frequency increases the THz amplitude increases and peak shift toward lower value of THz beat wave frequency due to the resonance condition 
$({\rm \omega} _{\rm c}^{\rm 2} + {\rm \omega} _{\rm p}^{\rm 2} )^{1/2}$. Thus, the peak appearing in the THz amplitude can be tuned by changing axially magnetic field value at a particular THz frequency.
Fig. 7. Plot of the normalized terahertz amplitude E THz/E 01 as a function of the normalized terahertz frequency ω/ωp at different normalized cyclotron frequency ωc/ωp.
Figure 8 shows that the efficiency ηTHz of the present scheme increases with cyclotron frequency ωc/ωp and decreases with laser beam width (a 0). Efficiency ~15% is achieved by beating of two hollow-Gaussian laser beams at beam width 
$a_0 \sim c/2{\rm \omega} _{\rm p} = 10 {\rm \mu m}$ and magnetic field ωc/ωp = 0.8, which is better than the results reported earlier. For instance, Sheng et al. (Reference Sheng, Wu, Li and Zhang2004) have obtained an efficiency of about 0.05% for THz emission using inhomogeneous plasma. Malik and Malik (Reference Malik and Malik2012) have reported the efficiency of about 0.2% by beating of two spatial-Gaussian lasers. Varshney et al. (Reference Varshney, Sajal, Singh, Kumar and Sharma2013) by using two x-mode lasers in a magnetized plasma have obtained an efficiency of about 1.5%. The maximum reported efficiency belongs to the work done by Singh and Malik (Reference Singh and Malik2014) and Bakhtiari et al. (Reference Bakhtiari, Yousefi, Golmohammady, Jazayeri and Ghafary2015b) in which the efficiency equal to 5.8% and 8.3% has been obtained, respectively. Thus, the present scheme can produce the THz radiation with high efficiency if the cosh-Gaussian lasers of higher decentered parameter (b) and small beam width (r 0) are used.
Fig. 8. Plot of the THz efficiency ηTHz as a function of normalized laser beam waist width r 0ωp/c at different values of normalized cyclotron frequency ωc/ωp.
Conclusions
We have proposed a model for the generation of THz radiation with high THz amplitude and high efficiency by using two cosh-Gaussian laser beams in axially magnetized rippled plasma. We have also considered the effect of electron-neutral collisions on THz generation. We have derived analytical equations for the electric field amplitude of THz and efficiency of THz radiation and then determined the resonance condition for THz radiation. We have found that the THz field amplitude and efficiency of THz radiation gets enhanced drastically in the magnetized plasma relative to the non-magnetized one. In non-magnetized plasma, the THz field amplitude and efficiency of THz radiation are very small, and they decrease considerably due to the electron-neutral collisions. In magnetized plasma, the negative consequences of electron-neutral collisions can be overcome by a magnetic field. In addition, the joint effect of the magnetic field and electron-neutral collisions causes a further enhancement of THz field amplitude and efficiency when the collision frequency is sufficiently low. This may be due to improved phase-matching condition and tunability due to magnetic field and plasma temperature. By optimizing the applied magnetic field, ripple frequency in plasma, laser beam parameters, and considering the beating, we demonstrate the THz radiation efficiency of up to ~15%. Finally, we have compared the THz radiation generated by hollow-Gaussian and Gaussian laser beams, and we have found that the THz radiation generated by hollow-Gaussian beams has three orders higher amplitude as compared with that generated by Gaussian laser beams, the efficiency of THz generated is five times higher in the case of hollow Gaussian beams.
