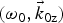1. INTRODUCTION
Nonlinear wave interactions and parametric instabilities in infinite plasmas have been studied extensively in the last decade because of its possible applications to laser fusion, plasma heating, and plasma current drive in fusion plasmas, as well as in space plasmas (Macchi et al., Reference Macchi, Battaglini, Cornolti, Lisseikina, Pegoraro, Ruhl and Vshivkov2002; Shoucri & Afeyan, Reference Shoucri and Afeyan2010; Verma & Sharma, Reference Verma and Sharma2011; Singh & Sharma, Reference Singh and Sharma2013; Hao et al., Reference Hao, Liu, Hu and Zheng2013; Vyas et al., Reference Vyas, Singh and Sharma2014). However such studies are rather few for bounded plasmas. Parametric decay of light wave into surface plasma wave (SPW) has been reported in literature because of its use for plasma diagnostics and for sustaining the plasma during plasma processing (Lee & Cho, Reference Lee and Cho1999; Kumar & Tripathi, Reference Kumar and Tripathi2007). SPW can exist at the boundary separating two dielectric media with permittivities opposite in sign (Liu & Tripathi, Reference Liu and Tripathi2000). The SPW can travel long distances along the interface and decays exponentially away from the interface in both media (decay is rapid in the conductor as compared with the dielectric). Hence the SPW field is localized in a thin skin layer. The properties of surface waves (SWs) propagating in bounded plasma structures are the subject of both experimental and theoretical studies. Their strong localization and resonant properties find application in solar cells and sensors etc., (Berndt et al., Reference Berndt, Gimzewski and Johansson1991; Shin and Fan, Reference Shin and Fan2006; Catchpole and Polman, Reference Catchpole and Polman2008; Rani et al., Reference Rani, Sharma and Sajal2013). When an intense electromagnetic wave is incident on bounded plasma, these surface wave modes become coupled parametrically through the incident pump wave and decay instability of the SWs is expected to occur under suitable conditions (Aliev & Brodin, Reference Aliev and Brodin1990; Brodin & Lundberg, Reference Brodin and Lundberg1991). The excitation of SPW by a laser pulse is not easily possible due to K-vector mismatch between the SPW and the laser. For a SPW propagating along the boundary of vacuum-metal interface (z-axis), the dispersion relation is given by Kz2 = (ω02/c 2)[ε /(1+ε )] where Kz is the wave vector of the SPW and ε is the dielectric constant of the metal (which is negative). The wave vector of the surface plasma wave is bigger than the wave vector of the electromagnetic wave in a vacuum. The K-vector mismatch can be overcome either by using the attenuated total reflection configuration or by creating a surface ripple of desired wave vector by a laser pulse (Kretschmann & Reather, Reference Kretschmann and Reather1968). Parashar et al. (Reference Prashar, Pandey and Tripathi1998) have developed a theory of the SPW excitation in the dense plasma via the stimulated Compton scattering. Lee & Cho (Reference Lee and Cho1999) have developed theoretical model for the nonlinear decay of a light wave into two daughter surface plasma waves. Shin et al. (Reference Shin, So, Jang, Won, Srivastava and Park2007) introduced the sub wavelength transmission of an effective surface plasmon beyond the light zone via the proximity interaction of convection electrons with a metal grating. Singh and Tripathi (Reference Singh and Tripathi2007) gave a theoretical model to excite surface plasma wave at frequency ω = ω1 − ω2 by beating of two coplanar laser beams of frequencies ω1 and ω2 impinged on a metal surface. The lasers exert a ponderomotive force on electrons in the skin layer and drive the SPW. The SPW heats the electrons efficiently, causing efficient ablation of the material. Kumar and Tripathi (Reference Kumar and Tripathi2007) suggested that the parametric decay of a light wave into pair of counter propagating SPWs at the vacuum–plasma interface is possible due to the plasma density perturbation at 2ω0 frequency associated with the ponderomotive force of the laser pulse on the plasma surface. The growth rate of the parametric process is the maximum for normal incidence of the laser pulse and it decreases with the angle of incidence. Recently, Tinakiche et al. (Reference Tinakiche, Annou and Tripathi2012) investigated three-wave coupling process in electron–positron-ion plasmas interacting with an electromagnetic pump wave.
In this paper, we have studied the stimulated Compton scattering of a surface plasma wave propagating on vacuum–metal interface. The SPW can be excited at the interface by a high-frequency laser (Liu & Tripathi, Reference Liu and Tripathi2000). The SPW ![]() $({{\rm \omega} _0},{\vec k_{0z}})$ acts as a pump and resonantly excites a quasi-electrostatic plasma mode along with a sideband SPW having frequency ω1 = ω − ω0 and wave number
$({{\rm \omega} _0},{\vec k_{0z}})$ acts as a pump and resonantly excites a quasi-electrostatic plasma mode along with a sideband SPW having frequency ω1 = ω − ω0 and wave number ![]() ${\vec k_{1{\rm z}}}\, = \,{\vec k_{\rm z}} - {\vec k_{0{\rm z}}}$. The density perturbation due to plasma wave couples with the oscillatory velocity of metal electrons (due to pump wave) and produce nonlinear current density
${\vec k_{1{\rm z}}}\, = \,{\vec k_{\rm z}} - {\vec k_{0{\rm z}}}$. The density perturbation due to plasma wave couples with the oscillatory velocity of metal electrons (due to pump wave) and produce nonlinear current density ![]() $(\vec J_1^{\;{\rm NL}} )$ driving the sideband SPW. The sideband wave couples nonlinearly with pump wave to exert a nonlinear ponderomotive force on metal electrons at the beat frequencies (ω0 = ω − ω1) driving the quasi-plasma mode having phase velocity equal to fermi velocity. The excited quasi-electrostatic fields can be utilized for heating plasma along with SPW by anomalous wave energy absorption mechanism. Growth rate equation is obtained on the basis of parametric coupling of a pump SPW, a plasma wave and a sideband SPW. Parametric coupling and conclusions are given in section II and III, respectively.
$(\vec J_1^{\;{\rm NL}} )$ driving the sideband SPW. The sideband wave couples nonlinearly with pump wave to exert a nonlinear ponderomotive force on metal electrons at the beat frequencies (ω0 = ω − ω1) driving the quasi-plasma mode having phase velocity equal to fermi velocity. The excited quasi-electrostatic fields can be utilized for heating plasma along with SPW by anomalous wave energy absorption mechanism. Growth rate equation is obtained on the basis of parametric coupling of a pump SPW, a plasma wave and a sideband SPW. Parametric coupling and conclusions are given in section II and III, respectively.
2. PARAMETRIC COUPLING
Consider the multilayered structure of glass (x < −a), metal (x < 0), and free space (x > 0). A laser is obliquely incident from the glass side on the glass–metal interface having field, given by (Liu & Tripathi, Reference Liu and Tripathi2000)
where ‘a’ is the width of the metal, θi is the angle of incidence and b′ = bcosθi and b is the spot size of laser. The incident laser excites a SPW on metal free space interface (x = 0) propagating along z-direction (as shown in Fig. 1). The electric field profile of the SPW ![]() $({{\rm \omega} _0},{\vec k_{0{\rm z}}};\,{\vec k_0} = {\vec k_{0{\rm z}}}\hat z - i{{\rm \alpha} _{\rm 0}}\hat x)$ is given by
$({{\rm \omega} _0},{\vec k_{0{\rm z}}};\,{\vec k_0} = {\vec k_{0{\rm z}}}\hat z - i{{\rm \alpha} _{\rm 0}}\hat x)$ is given by
where ![]() ${A_{{\rm 0z}}} = {A_{0{\rm s}}}\left( {\hat z - \displaystyle{{i{k_{0{\rm z}}}} \over {{{\rm \alpha} _0}}}\hat x} \right){e^{{{\rm \alpha} _0}x}}$ (x < 0, metal)
${A_{{\rm 0z}}} = {A_{0{\rm s}}}\left( {\hat z - \displaystyle{{i{k_{0{\rm z}}}} \over {{{\rm \alpha} _0}}}\hat x} \right){e^{{{\rm \alpha} _0}x}}$ (x < 0, metal)
![]() $A_{0z} = A_{0{\rm s}}\bigg( {\hat z} + \displaystyle{{i{k_{0z}}} \over {{\rm \alpha}_{0}^{\prime}{\hat x}} }\bigg)e^{ - {\rm \alpha}_{0}^{\prime}x}$ (x > 0, vacuum)
$A_{0z} = A_{0{\rm s}}\bigg( {\hat z} + \displaystyle{{i{k_{0z}}} \over {{\rm \alpha}_{0}^{\prime}{\hat x}} }\bigg)e^{ - {\rm \alpha}_{0}^{\prime}x}$ (x > 0, vacuum)

Fig. 1. Schematic of surface plasma wave Compton scattering at the vacuum–metal interface.
The amplitude of the wave for the free space at x = 0 and z = 0 is given by
where T 00 = (2iψ1e α0a)/(1+iψ1)
 $${{\rm \psi} _1} = \displaystyle{{{{\rm \eta} _{\rm g}}} \over {{{\left \vert {1 + {{{\rm \varepsilon ^{\prime}}}_0}(1 - 1/{\rm \eta} _{\rm g}^2 )} \right \vert} ^{1/2}}}}$$
$${{\rm \psi} _1} = \displaystyle{{{{\rm \eta} _{\rm g}}} \over {{{\left \vert {1 + {{{\rm \varepsilon ^{\prime}}}_0}(1 - 1/{\rm \eta} _{\rm g}^2 )} \right \vert} ^{1/2}}}}$$ $${{\rm \psi} _2} = \displaystyle{{2(1 + i{{\rm \psi} _1}){{\rm \omega} _0}{{\left \vert {{{{\rm \varepsilon ^{\prime}}}_0}} \right \vert} ^{3/2}}} \over {(1 - i{{\rm \psi} _1})c{{\left \vert {1 + {{{\rm \varepsilon ^{\prime}}}_0}} \right \vert} ^{1/2}}({{{\rm \varepsilon ^{\prime}}}_0}^2 - 1)}}$$
$${{\rm \psi} _2} = \displaystyle{{2(1 + i{{\rm \psi} _1}){{\rm \omega} _0}{{\left \vert {{{{\rm \varepsilon ^{\prime}}}_0}} \right \vert} ^{3/2}}} \over {(1 - i{{\rm \psi} _1})c{{\left \vert {1 + {{{\rm \varepsilon ^{\prime}}}_0}} \right \vert} ^{1/2}}({{{\rm \varepsilon ^{\prime}}}_0}^2 - 1)}}$$ $$I = \int\limits_{ - \infty} ^\infty {\displaystyle{{{e^{ - {{\rm p}^2}}}(\,p - {{\rm \sigma} _1}b/2 + i{{\rm \sigma} _2}b/2)} \over {({{(\,p - {{\rm \sigma} _1}b/2)}^2} + {{({{\rm \sigma} _2}b/2)}^2})}}} {\rm dp}$$
$$I = \int\limits_{ - \infty} ^\infty {\displaystyle{{{e^{ - {{\rm p}^2}}}(\,p - {{\rm \sigma} _1}b/2 + i{{\rm \sigma} _2}b/2)} \over {({{(\,p - {{\rm \sigma} _1}b/2)}^2} + {{({{\rm \sigma} _2}b/2)}^2})}}} {\rm dp}$$ In the above expression ηg = 1.5, ψ2exp(−2α0a) = σ1 + iσ2, α02 = k 0z2 − (ω02/c 2)ε0′ and α0′2 = k 0z2 − (ω02/c 2). The dielectric constant of the metal at frequency ω0 is given by ε0′ = εl − ωp2/ω02. εl and ![]() ${{\rm \omega} _{\rm p}}\, = \,\sqrt {{{{n_0}{e^2}} / {m{\rm \varepsilon}}}} $ are the lattice permittivity of metal and plasma frequency, respectively, ε = 8.854 × 10−12 f/m, n 0 = 5.85 × 1028/m3 for silver metal; −e and m is the charge and effective mass of electron, respectively. On applying conditions of continuity ε0′E 0x and E 0z at x = 0 along x and z directions, the dispersion relation of the SPW is given by
${{\rm \omega} _{\rm p}}\, = \,\sqrt {{{{n_0}{e^2}} / {m{\rm \varepsilon}}}} $ are the lattice permittivity of metal and plasma frequency, respectively, ε = 8.854 × 10−12 f/m, n 0 = 5.85 × 1028/m3 for silver metal; −e and m is the charge and effective mass of electron, respectively. On applying conditions of continuity ε0′E 0x and E 0z at x = 0 along x and z directions, the dispersion relation of the SPW is given by
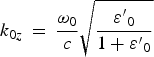 $${k_{0z}}\, = \,\displaystyle{{{{\rm \omega} _0}} \over c}\sqrt {\displaystyle{{{{{\rm \varepsilon ^{\prime}}}_0}} \over {1 + {{{\rm \varepsilon ^{\prime}}}_0}}}} $$
$${k_{0z}}\, = \,\displaystyle{{{{\rm \omega} _0}} \over c}\sqrt {\displaystyle{{{{{\rm \varepsilon ^{\prime}}}_0}} \over {1 + {{{\rm \varepsilon ^{\prime}}}_0}}}} $$ The pump SPW imparts oscillatory velocity to electrons![]() $({\vec v_0} = e{\vec E_0}/mi{{\rm \omega} _0})$. At resonance, the pump SPW decay into a quasi-electrostatic plasma wave
$({\vec v_0} = e{\vec E_0}/mi{{\rm \omega} _0})$. At resonance, the pump SPW decay into a quasi-electrostatic plasma wave ![]() $({\rm \omega}, {\vec k_z})$ of potential (ϕ),
$({\rm \omega}, {\vec k_z})$ of potential (ϕ),
and a sideband SPW ![]() $({{\rm \omega} _1},{\vec k_{1z}};{\vec k_1} = {k_{1z}}\hat z - i{{\rm \alpha} _1}\hat x)$ of electric field
$({{\rm \omega} _1},{\vec k_{1z}};{\vec k_1} = {k_{1z}}\hat z - i{{\rm \alpha} _1}\hat x)$ of electric field ![]() $({\vec E_1})$$
$({\vec E_1})$$
where ![]() ${A_{1{\rm z}}} = {A_1}\left( {\hat z - \displaystyle{{i{k_{1{\rm z}}}} \over {{{\rm \alpha} _{\rm 1}}}}\hat x} \right){e^{{\rm \alpha} 1x}}$ (x < 0, metal)
${A_{1{\rm z}}} = {A_1}\left( {\hat z - \displaystyle{{i{k_{1{\rm z}}}} \over {{{\rm \alpha} _{\rm 1}}}}\hat x} \right){e^{{\rm \alpha} 1x}}$ (x < 0, metal)
![]() ${A_{1{\rm z}}} = {A_1}\left( {\hat z + \displaystyle{{i{k_{1{\rm z}}}} \over {{\rm \alpha} {{\rm ^{\prime}}_{\rm 1}}}}\hat x} \right){e^ -} ^{{\rm \alpha} 1x} $ (x > 0, vacuum)
${A_{1{\rm z}}} = {A_1}\left( {\hat z + \displaystyle{{i{k_{1{\rm z}}}} \over {{\rm \alpha} {{\rm ^{\prime}}_{\rm 1}}}}\hat x} \right){e^ -} ^{{\rm \alpha} 1x} $ (x > 0, vacuum)
where α12 = k 1z2 − (ω12/c 2)ε1 and α1′2 = k 1z2 − (ω12/c 2). The dielectric constant of sideband SPW at frequency ω1 is ε1 = εl − ωp2/ω12. The phase matching conditions for parametric decay are ![]() ${\vec k_{\rm z}} = {\vec k_{0{\rm z}}} + {\vec k_{1{\rm z}}}$ and ω = ω0 + ω1. The sideband SPW imparts oscillatory velocity to electrons
${\vec k_{\rm z}} = {\vec k_{0{\rm z}}} + {\vec k_{1{\rm z}}}$ and ω = ω0 + ω1. The sideband SPW imparts oscillatory velocity to electrons ![]() $({\vec v_1} = e{\vec E_1}/mi{{\rm \omega} _1})$ and couples nonlinearly with the pump wave to exert a ponderomotive force on electrons at frequency ω, which is given by
$({\vec v_1} = e{\vec E_1}/mi{{\rm \omega} _1})$ and couples nonlinearly with the pump wave to exert a ponderomotive force on electrons at frequency ω, which is given by
Replace ![]() $\vec v$ by
$\vec v$ by ![]() ${\vec v_0} + {\vec v_1}$ and
${\vec v_0} + {\vec v_1}$ and ![]() ${\vec B}$ by
${\vec B}$ by ![]() ${\vec B_0} + {\vec B_1}$ in the above equation, where
${\vec B_0} + {\vec B_1}$ in the above equation, where ![]() ${\vec B_0} = i{\vec k_0} \times {\vec E_0}/i{{\rm \omega} _0}$ and
${\vec B_0} = i{\vec k_0} \times {\vec E_0}/i{{\rm \omega} _0}$ and ![]() ${\vec B_1} = i{\vec k_1} \times {\vec E_1}/i{{\rm \omega} _1}$ for pump and sideband SPW, respectively. On substituting these values into Eq. (7), we obtained
${\vec B_1} = i{\vec k_1} \times {\vec E_1}/i{{\rm \omega} _1}$ for pump and sideband SPW, respectively. On substituting these values into Eq. (7), we obtained
where ![]() ${\Phi _{\rm p}}\, = \,{A_{0s}}(x)\;{A_1}(x)\left( {\displaystyle{e \over {2m{{\rm \omega} _0}{{\rm \omega} _1}}}} \right)\left( {1 \!- \displaystyle{{{k_{0z}}{k_{1z}}} \over {{{\rm \alpha} _0}{{\rm \alpha} _1}}}} \right){e^{ - i({\rm \omega} t - {k_{\rm z}}z)}}$, termed as ponderomotive potential.
${\Phi _{\rm p}}\, = \,{A_{0s}}(x)\;{A_1}(x)\left( {\displaystyle{e \over {2m{{\rm \omega} _0}{{\rm \omega} _1}}}} \right)\left( {1 \!- \displaystyle{{{k_{0z}}{k_{1z}}} \over {{{\rm \alpha} _0}{{\rm \alpha} _1}}}} \right){e^{ - i({\rm \omega} t - {k_{\rm z}}z)}}$, termed as ponderomotive potential.
This ponderomotive force along with self-consistent low-frequency field on the metal free electrons drive plasma oscillations at frequency ω. Hence, the equation of motion of electron becomes
where υ is the collision frequency. Here, the collisions are considered effective only for low-frequency plasma wave for which phase velocity is close to the Fermi velocity of free electrons. For high-frequency SPWs collisional effects are neglected. The oscillatory velocity ![]() $({\vec v_{\rm \omega}} )$ of electron at frequency (ω) is obtained by solving above equation of motion, given by
$({\vec v_{\rm \omega}} )$ of electron at frequency (ω) is obtained by solving above equation of motion, given by
 $${\vec v_{\rm \omega}} = - \displaystyle{{e\left[ { - i\nabla {\Phi _{\rm p}} - i\displaystyle{{\partial {\rm \phi}} \over {\partial x}}\hat x + {k_z}{\rm \phi} \,\hat z} \right]} \over {m({\rm \omega} + i{\rm \upsilon} )}}$$
$${\vec v_{\rm \omega}} = - \displaystyle{{e\left[ { - i\nabla {\Phi _{\rm p}} - i\displaystyle{{\partial {\rm \phi}} \over {\partial x}}\hat x + {k_z}{\rm \phi} \,\hat z} \right]} \over {m({\rm \omega} + i{\rm \upsilon} )}}$$ Substituting the value of oscillatory velocity from Eq. (9) into continuity equation ![]() $(\partial n/\partial t + \nabla \cdot ({n_0}{\vec v_{\rm \omega}} ) = 0)$, we obtain the density perturbation (n) due to oscillatory motion of metal electrons.where χe = −ωp2/ω (ω +iυ).
$(\partial n/\partial t + \nabla \cdot ({n_0}{\vec v_{\rm \omega}} ) = 0)$, we obtain the density perturbation (n) due to oscillatory motion of metal electrons.where χe = −ωp2/ω (ω +iυ).
n 0 is the electron density inside the metal. Using n in Poisson's equation, we get
The density perturbations couples with oscillatory movement of metal electrons at frequency ω0 (due to pump SPW) and excites a nonlinear current density ![]() $(\vec J_1^{{\,\,\rm NL}} )$ at the sideband frequency ω1, which is given by
$(\vec J_1^{{\,\,\rm NL}} )$ at the sideband frequency ω1, which is given by
On substituting values of n and ![]() $v_0^{\ast} $ (
$v_0^{\ast} $ (![]() $v_0^{\ast} = - e{\vec E_0}/mi{{\rm \omega} _0}$, oscillatory velocity of electrons at frequency ω0), the nonlinear current density is given by
$v_0^{\ast} = - e{\vec E_0}/mi{{\rm \omega} _0}$, oscillatory velocity of electrons at frequency ω0), the nonlinear current density is given by
This nonlinear current density ![]() $(\vec J_1^{{\,\,\rm NL}} )$ is responsible for the growth of sideband SPW whose characteristic equation can be derived by solving wave equation. The wave equation governing electric field of SPW at the sideband frequency can be written as
$(\vec J_1^{{\,\,\rm NL}} )$ is responsible for the growth of sideband SPW whose characteristic equation can be derived by solving wave equation. The wave equation governing electric field of SPW at the sideband frequency can be written as
Taking the divergence of the Eq. (13), we obtain
Substituting Eq. (14) into Eq. (13), we obtain
After the Fourier analysis of Eq. (15), we have
 $$\displaystyle{{{\rm \omega} _1^2 - {\rm \omega} _{1{\rm r}}^2} \over {{c^2}}}{{\rm \varepsilon} _1}{\vec E_1} = \displaystyle{{4{\rm \pi} i{{\rm \omega} _1}} \over {{c^2}}}\vec J_1^{{\,\,\rm NL}} \displaystyle{{4{\rm \pi} i{{\rm \omega} _1}} \over {{\rm \omega} _1^2 {{\rm \varepsilon} _1}}}\nabla (\nabla \cdot \vec J_1^{{\,\,\rm NL}} )$$
$$\displaystyle{{{\rm \omega} _1^2 - {\rm \omega} _{1{\rm r}}^2} \over {{c^2}}}{{\rm \varepsilon} _1}{\vec E_1} = \displaystyle{{4{\rm \pi} i{{\rm \omega} _1}} \over {{c^2}}}\vec J_1^{{\,\,\rm NL}} \displaystyle{{4{\rm \pi} i{{\rm \omega} _1}} \over {{\rm \omega} _1^2 {{\rm \varepsilon} _1}}}\nabla (\nabla \cdot \vec J_1^{{\,\,\rm NL}} )$$ Taking the dot product of Eq. (16) with ![]() $\vec E_1^{\ast} $ and integrating from −∞ to ∞ with respect to x, we have
$\vec E_1^{\ast} $ and integrating from −∞ to ∞ with respect to x, we have
 $$\eqalign{& \displaystyle{{{\rm \omega }_1^2 - {\rm \omega }_{1{\rm r}}^2 } \over {{c^2}}}\left[ {\int_{ - \infty }^0 {{{\rm \varepsilon }_1}{{\vec E}_1} \cdot \vec E_1^{\ast} {\rm d}x} + \int_0^\infty {{{\vec E}_1} \cdot \vec E_1^{\ast} {\rm d}x} } \right] \cr & \quad = - \displaystyle{{4{\rm \pi }i{{\rm \omega }_1}} \over {{c^2}}}\int_{ - \infty }^0 {\vec J_{1}^{\,\,{\rm NL}} \cdot \vec E_1^{\ast} {\rm d}x} - \displaystyle{{4{\rm \pi }i{{\rm \omega }_1}} \over {{\rm \omega }_1^2 {{\rm \varepsilon }_1}}} \cr & \quad \quad \int_{ - \infty }^0 {\nabla (\nabla \cdot \vec J_{1}^{\,\,{\rm NL}} )} \cdot \vec E_1^{\ast} {\rm d}x} $$
$$\eqalign{& \displaystyle{{{\rm \omega }_1^2 - {\rm \omega }_{1{\rm r}}^2 } \over {{c^2}}}\left[ {\int_{ - \infty }^0 {{{\rm \varepsilon }_1}{{\vec E}_1} \cdot \vec E_1^{\ast} {\rm d}x} + \int_0^\infty {{{\vec E}_1} \cdot \vec E_1^{\ast} {\rm d}x} } \right] \cr & \quad = - \displaystyle{{4{\rm \pi }i{{\rm \omega }_1}} \over {{c^2}}}\int_{ - \infty }^0 {\vec J_{1}^{\,\,{\rm NL}} \cdot \vec E_1^{\ast} {\rm d}x} - \displaystyle{{4{\rm \pi }i{{\rm \omega }_1}} \over {{\rm \omega }_1^2 {{\rm \varepsilon }_1}}} \cr & \quad \quad \int_{ - \infty }^0 {\nabla (\nabla \cdot \vec J_{1}^{\,\,{\rm NL}} )} \cdot \vec E_1^{\ast} {\rm d}x} $$Here, ε1 = εl − ωp2/ω12 for metal (x < 0) and ε1 = 1 for vacuum (x > 0). Further, substituting the value of nonlinear current from Eq. (12). Then Eq. (17)
 $$\eqalign{ {\rm \omega }_1^2 - {\rm \omega }_{1{\rm r}}^2 & = - \displaystyle{{{e^2}{k^2}{{\rm \chi }_e}} \over {4{m^2}{\rm \omega }_0^2 {\rm \omega }_1^2 {{\rm \varepsilon }_1}}}\left( {\displaystyle{{{{\rm \varepsilon }_{\rm l}}} \over {{{\rm \varepsilon }_{\rm l}} + {{\rm \chi }_e}}}} \right)\left( {1 - \displaystyle{{{k_{0z}}{k_{1z}}} \over {{{\rm \alpha }_0}{{\rm \alpha }_1}}}} \right)\left( {\displaystyle{{{{\rm \alpha }_1}{{{\rm \alpha '}}_1}} \over {{{\rm \alpha }_0} + {{\rm \alpha }_1}}}} \right) \cr & \quad \displaystyle{{\left[ {{\rm \omega }_1^2 {{\rm \varepsilon }_1} - {c^2}k_{1z}^2 + {c^2}{{(2{{\rm \alpha }_0} + {{\rm \alpha }_1})}^2}} \right]} \over {({{\rm \varepsilon }_1}{{{\rm \alpha '}}_1} - {{\rm \alpha }_1})}}\vert{E_0}\vert{^2}} $$
$$\eqalign{ {\rm \omega }_1^2 - {\rm \omega }_{1{\rm r}}^2 & = - \displaystyle{{{e^2}{k^2}{{\rm \chi }_e}} \over {4{m^2}{\rm \omega }_0^2 {\rm \omega }_1^2 {{\rm \varepsilon }_1}}}\left( {\displaystyle{{{{\rm \varepsilon }_{\rm l}}} \over {{{\rm \varepsilon }_{\rm l}} + {{\rm \chi }_e}}}} \right)\left( {1 - \displaystyle{{{k_{0z}}{k_{1z}}} \over {{{\rm \alpha }_0}{{\rm \alpha }_1}}}} \right)\left( {\displaystyle{{{{\rm \alpha }_1}{{{\rm \alpha '}}_1}} \over {{{\rm \alpha }_0} + {{\rm \alpha }_1}}}} \right) \cr & \quad \displaystyle{{\left[ {{\rm \omega }_1^2 {{\rm \varepsilon }_1} - {c^2}k_{1z}^2 + {c^2}{{(2{{\rm \alpha }_0} + {{\rm \alpha }_1})}^2}} \right]} \over {({{\rm \varepsilon }_1}{{{\rm \alpha '}}_1} - {{\rm \alpha }_1})}}\vert{E_0}\vert{^2}} $$
where χe = − ωp2/ω (ω +iυ), ![]() ${k_{{\rm 0z}}} = {{\rm \omega} _0}/c\sqrt {{{{\rm \varepsilon '}}_0}/1 + {{{\rm \varepsilon '}}_0}} $,
${k_{{\rm 0z}}} = {{\rm \omega} _0}/c\sqrt {{{{\rm \varepsilon '}}_0}/1 + {{{\rm \varepsilon '}}_0}} $, ![]() ${k_{1{\rm z}}} = $
${k_{1{\rm z}}} = $![]() $ {{\rm \omega} _1}/c\sqrt {{{\rm \varepsilon} _1}/1 + {{\rm \varepsilon} _1}} $, α02 = k 0z2 − (ω02/c 2)ε0′, α12 = k 1z2 − (ω12/c 2)ε1 and α1′2 = k 1z2 − (ω12/c 2). Eq. (18) is the dispersion relation for Compton process. Growth rate (γ) for the process can be deduced by solving Eq. (18) that comes out as follows:
$ {{\rm \omega} _1}/c\sqrt {{{\rm \varepsilon} _1}/1 + {{\rm \varepsilon} _1}} $, α02 = k 0z2 − (ω02/c 2)ε0′, α12 = k 1z2 − (ω12/c 2)ε1 and α1′2 = k 1z2 − (ω12/c 2). Eq. (18) is the dispersion relation for Compton process. Growth rate (γ) for the process can be deduced by solving Eq. (18) that comes out as follows:
 $$\eqalign{ {\rm \gamma }\, & = \, - \displaystyle{{{e^2}{k^2}{\rm \varepsilon }_l^2 {\rm \omega} {\rm \upsilon }} \over {8{m^2}{\rm \omega }_0^2 {\rm \omega }_{\rm p}^{\rm 2} {{({\rm \omega } - {{\rm \omega }_0})}^3}}}\left( {1 - \displaystyle{{{k_{0z}}{k_{1z}}} \over {{{\rm \alpha }_0}{{\rm \alpha }_1}}}} \right)\left( {\displaystyle{{{{\rm \alpha }_1}{{{\rm \alpha '}}_1}} \over {{{\rm \alpha }_0} + {{\rm \alpha }_1}}}} \right) \cr & \quad \left( {\displaystyle{{{{({\rm \omega } - {{\rm \omega }_0})}^2}{{\rm \varepsilon }_1} - {c^2}k_{{\rm 1z}}^{\rm 2} + {c^2}{{(2{{\rm \alpha }_0} + {{\rm \alpha }_1})}^2}} \over {({{\rm \varepsilon }_1}{{{\rm \alpha '}}_1} - {{\rm \alpha }_1})}}} \right){\left\vert {{E_0}} \right\vert^2}} $$
$$\eqalign{ {\rm \gamma }\, & = \, - \displaystyle{{{e^2}{k^2}{\rm \varepsilon }_l^2 {\rm \omega} {\rm \upsilon }} \over {8{m^2}{\rm \omega }_0^2 {\rm \omega }_{\rm p}^{\rm 2} {{({\rm \omega } - {{\rm \omega }_0})}^3}}}\left( {1 - \displaystyle{{{k_{0z}}{k_{1z}}} \over {{{\rm \alpha }_0}{{\rm \alpha }_1}}}} \right)\left( {\displaystyle{{{{\rm \alpha }_1}{{{\rm \alpha '}}_1}} \over {{{\rm \alpha }_0} + {{\rm \alpha }_1}}}} \right) \cr & \quad \left( {\displaystyle{{{{({\rm \omega } - {{\rm \omega }_0})}^2}{{\rm \varepsilon }_1} - {c^2}k_{{\rm 1z}}^{\rm 2} + {c^2}{{(2{{\rm \alpha }_0} + {{\rm \alpha }_1})}^2}} \over {({{\rm \varepsilon }_1}{{{\rm \alpha '}}_1} - {{\rm \alpha }_1})}}} \right){\left\vert {{E_0}} \right\vert^2}} $$where ω1 = ω1r+iγ and k 2 = (α0 + α1)2 − (k 0z + k 1z)2.
Eq. (19) is normalized and numerically solved using the parameters εl = 4, T e = 63600 K (Fermi temperature for silver) and ωp = 2.17 × 1015 rad/s. The growth rate of Compton process increases with the frequency of incident laser and turns out to be 2.5 × 10−5 ωp at laser frequency ω0 = 0.35ωp for incident laser amplitude A 0L = 0.3 mωpc/e, laser spot size b = 100c/ωp. Here, width of the metal is (aω0/c) = 0.5 and free electron density of silver metal is n 0 = 5.85 × 1028/m3. The frequency of quasi-static plasma mode can be calculated from the resonance condition ![]() ${\vec k_{0{\rm z}}}\, = \,{\vec k_{\rm z}} - {\vec k_{1{\rm z}}}$ where
${\vec k_{0{\rm z}}}\, = \,{\vec k_{\rm z}} - {\vec k_{1{\rm z}}}$ where ![]() ${\vec k_{\rm z}} = {\rm \omega} /{v_{\rm F}}$. Here, v F is the Fermi velocity of electrons for silver. Figure 2 depicts the variation of plasma mode frequency (ω/ωp) with pump frequency (ω/ωp). Here, plasma frequency increases linearly with frequency of pump wave. This is due to the fact that with increase in pump frequency, there is corresponding increase in its wave number. Hence, to satisfy the resonance conditions, there should be a related increase in the plasma mode frequency. Amplitude of SPW (eA 0S/mωpc) is plotted as a function of incident laser spot size (bωp/c) on varying width of the metal film (bω0/c) and amplitude of laser (eA 0L/mωpc) in Figures 3a and 3b, respectively. Figure 3a shows that for smaller values of spot size, the amplitude of SPW increases linearly and saturates at higher values of bωp/c. From Eq. (3), the amplitude of SPW is larger than the laser amplitude for the condition bωp/c > exp(aω0/c), where b and a are the spot size of laser and the width of the metal, respectively (Liu & Tripathi, Reference Liu and Tripathi2000). On increasing b and keeping a fixed, the inequality grows, resulting in increased amplitude of the SPW as observed in Figure 3a. The saturation value of amplitude is larger for metal films of larger width and it occurs at larger spot size of the laser. For (aω0/c = 0.5), the amplitude of SPW further increases with the laser amplitude as observed in Figure 3b. As the laser intensity increases, evanescent wave provides higher oscillatory velocity to the electrons and couple with the pump wave to exert ponderomotive on electron at (
${\vec k_{\rm z}} = {\rm \omega} /{v_{\rm F}}$. Here, v F is the Fermi velocity of electrons for silver. Figure 2 depicts the variation of plasma mode frequency (ω/ωp) with pump frequency (ω/ωp). Here, plasma frequency increases linearly with frequency of pump wave. This is due to the fact that with increase in pump frequency, there is corresponding increase in its wave number. Hence, to satisfy the resonance conditions, there should be a related increase in the plasma mode frequency. Amplitude of SPW (eA 0S/mωpc) is plotted as a function of incident laser spot size (bωp/c) on varying width of the metal film (bω0/c) and amplitude of laser (eA 0L/mωpc) in Figures 3a and 3b, respectively. Figure 3a shows that for smaller values of spot size, the amplitude of SPW increases linearly and saturates at higher values of bωp/c. From Eq. (3), the amplitude of SPW is larger than the laser amplitude for the condition bωp/c > exp(aω0/c), where b and a are the spot size of laser and the width of the metal, respectively (Liu & Tripathi, Reference Liu and Tripathi2000). On increasing b and keeping a fixed, the inequality grows, resulting in increased amplitude of the SPW as observed in Figure 3a. The saturation value of amplitude is larger for metal films of larger width and it occurs at larger spot size of the laser. For (aω0/c = 0.5), the amplitude of SPW further increases with the laser amplitude as observed in Figure 3b. As the laser intensity increases, evanescent wave provides higher oscillatory velocity to the electrons and couple with the pump wave to exert ponderomotive on electron at (![]() ${\rm \omega}, \,{\vec k_{\rm z}}$) and excites the SPW of higher amplitude. Enhanced amplitude of SPW at metal free space interface is reported by Raether (Reference Raether1988) and Liu and Tripathi, (Reference Liu and Tripathi1998).
${\rm \omega}, \,{\vec k_{\rm z}}$) and excites the SPW of higher amplitude. Enhanced amplitude of SPW at metal free space interface is reported by Raether (Reference Raether1988) and Liu and Tripathi, (Reference Liu and Tripathi1998).

Fig. 2. Variation of normalized plasma wave frequency (ω/ωp) with normalized pump wave frequency (ω0/ωp).

Fig. 3. Plot of surface plasma wave amplitude versus laser spot size (bωp/c) on varying (a) width of the metal layer (bω0/c) for (eA 0L/mωpc) = 0.3 and (b) laser amplitude (eA 0L/mωpc) for (aω0/c) = 0.5.
Figure 4 shows the variation of SPW amplitude with pump frequency and width of the metal. Other parameters are (eA 0L/mωpc) = 0.3 and (bωp/c) = 100. As the metal thickness increases, the evanescent field has to penetrate longer distances to excite the SPW. Also, the condition [bω0/c > exp(aω0/c)] approaches towards equality on increasing a, resulting in decrease of SPW amplitude with the metal width as observed in Figure 4. In Figures 5a and 5b, growth rate (γ/ωp) of the Compton process is plotted as a function of pump frequency for various combinations of laser spot size and its amplitude for (aω0/c) = 0.5. The growth rate of the Compton process increases with the pump frequency because SPW is strongly localized near the interface and propagates along the interface with low attenuation. Increased amplitude of the SPW at the metal free space interface as observed in Figures 3a and 3b enhances the ponderomotive force [Eq. (8)] on electrons. As a result, the growth rate increases with incident laser spot size and its amplitude as shown in Figures 5a and 5b, respectively. Lee and Cho (Reference Lee and Cho1999) theoretically investigated the decay of high-frequency light wave into two daughter SWs and reported the increase in growth rate of the surface wave with the light wave frequency. Drake et al. (Reference Drake, Baldis, Kruer, Williams, Estabrook, Johnston and Young1990) have experimentally studied the stimulated Compton scattering on electrons from laser produced plasma and reported that stimulated Compton scattering increases with the laser intensity. Variation of growth rate of the Compton process with width of the metal is plotted in Figure 6. Other parameters are same as Figure 4. Increased width of the metal surface leads to lesser amplitude of SPW at the metal free space interface and lesser ponderomotive force on electrons to drive the quasi-static plasma mode, resulting in decrease of growth rate with the metal width.

Fig. 4. Plot of surface plasma wave amplitude versus pump frequency and width of metal. The other parameters are (eA 0L/mωpc) = 0.3 and (bωp/c) = 100.

Fig. 5. Plot of growth rate (γ/ωp) of the Compton process versus pump frequency on varying (a) spot size of laser for (eA 0L/mωpc) = 0.3 and (b) its amplitude for (bωp/c) = 100 at (aω0/c) = 0.5.

Fig. 6. Variation of growth rate of the Compton process versus pump frequency on varying width of the metal. The other parameters are (eA 0L/mωpc) = 0.3 & (bωp/c) = 100.
3. CONCLUSIONS
In this work, we discussed Compton scattering of SPW propagating at the metal–vacuum interface. This wave can be excited by a high-frequency laser. The parametric decay of SPW into another SPW can be realized via quasi-static plasma wave in metals. The quasi-static plasma wave is damped (as its phase velocity is equal to the Fermi velocity (v F) of the metal), by the free electrons, resulting into surface heating. Growth rate of the Compton process increases with the pump wave frequency, width of the metal layer, laser amplitude, and its spot size. It increases threefold as the frequency increases from 0.25 to 0.35ωp. However, growth rate of Compton process is found to decrease with the width of metal layer for higher values of pump frequency. As this process is sensitive to pump frequency variation, one can suitably choose among available lasers for material processing. The Compton process can produce energetic electrons travelling along the plasma boundary. These electrons in turn can give rise to stronger X-ray emission which can be utilized for various purposes along with the plasma diagnostics (Shivarova et al., Reference Shivarova, Stoychev and Russeva1975; Zhaoquan, et al., Reference Zhaoquan, Guangqing, Minghai, Yelin, Xiaoliang, Ping, Qiyan and Xiwei2012).