Published online by Cambridge University Press: 01 March 2004
Measurements of the ion emission from targets irradiated with neodymium glass and iodine lasers were analyzed and a very significant anomaly observed. The fastest ions with high charge number Z, which usually are of megaelectron volt energy following the relativistic self-focusing and nonlinear-force acceleration theory, were reduced to less than 50 times lower energies when 1.2 ps laser pulses of about 1 J were incident. We clarify this discrepancy by the model of skin depth plasma front interaction in contrast to the relativistic self-focusing with filament generation. This was indicated also from the unique fact that the ion number was independent of the laser intensity. The skin layer theory prescribes prepulse control and lower (near relativistic threshold) laser intensities for nonlinear-force-driven plasma blocks for high-gain ignition similar to light ion beam fusion.
Studying the ion emission from laser-produced plasmas resulted in new aspects for the application in laser fusion after the chirped pulse amplification (CPA) of Mourou (Strickland & Mourou, 1985; Mourou & Tajima, 2002) provided laser pulses of picosecond duration and powers greater than terawatts. For longer pulses in the range of nanoseconds, it is well known (Begay et al., 1983; Haseroth & Hora, 1996) that the emission of ions with several hundred megaelectron volts are generated at laser irradiation of targets as expected from relativistic self-focusing (Hora, 1975; Jones et al., 1982; Osman et al., 1999; Hora, 1991, 2000a), where however the ions are emitted nearly isotropic or with some preferential direction perpendicular to the laser beam (Basov et al., 1987; Häuser et al., 1992). What is new with the picosecond interaction is that very intense directed beams are produced into the direction of the laser beam. Light ion beams may be interesting for producing spark ignition in laser fusion (Roth et al., 2001). In other cases, directed electron beams (Umstadter et al., 1996; Hora et al., 2000b; Gahn et al., 2000) were observed. Such electron beams should ignite fusion detonation fronts in large amounts of low compressed (10 times the solid state) DT where 10 kJ of laser pulses are expected to produce 100 MJ fusion energy (Nuckolls & Wood, 2002).
In contrast to these cases of beam generation of particle beams by relativistic effects, we present here a mechanism (Hora et al., 2002a; Hora, 2003) derived from experiments (Badziak et al., 1999, 2003) where the picosecond–terawatt interaction produces plane plasma blocks and where relativistic self-focusing had to be avoided very carefully. We report here how the block moving in the direction of the laser light may act as a very intense light ion beam to produce a fusion reaction front in uncompressed solid DT just as known from the earlier discussed scheme of light ion beam fusion (Hora, 1983) based on an extensive discussion of the fusion detonation front as a laser driven flame (Bobin, 1971, 1974; Chu, 1972).
A very surprising result was measured when 1.5-ps neodymium glass laser pulses of up to 350 mJ energy irradiated copper targets when prepulses were sufficiently suppressed (Badziak et al., 1999). The maximum energy of the (energetic linear) Z-separated Cu+13 ions of 450 keV from picosecond target irradiation was more than 50 times lower than the value known for nanosecond laser pulses of the same power of 22 MeV in agreement with the relativistic self-focusing theory (Hora, 1975; Hora et al., 1978; Jones et al., 1982; Haseroth & Hora, 1996; Osman et al., 1999) and subsequent nonlinear-force acceleration of the electron cloud (Hora, 2000a; Hora et al., 2000b) similar to all the usual experiments. The measurements with the much lower ion energy (Badziak et al., 1999) showed another very unusual property: when the laser energy EL was varied from 15 to 350 mJ, no change of the ion number occurred, only the ion energy increased linearly on the EL. This led us to the conclusion of a skin depth interaction process (Fig. 1b) in contrast to the usual relativistic self-focusing process (Fig. 1a).
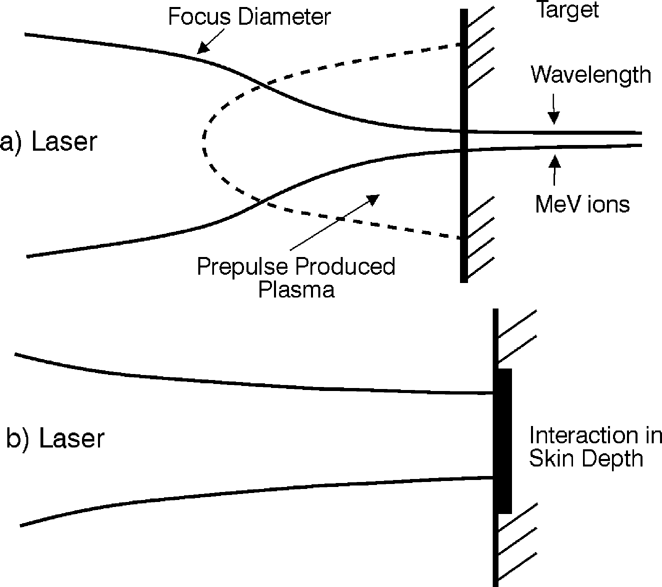
Scheme of laser–plasma interaction with relativistic self-focusing (Hora, 1975; Osman et al., 1999; Hora, 2000a, 2000b) (a) where the long irradiation produced a plasma cloud above the target permitting (relativistic) self-focusing in contrast to the plane wave interaction in the skin layer scheme and (b) without the plasma for self-focusing but with plane geometry acceleration of the laser-irradiated electron cloud following the nonlinear (ponderomotive) force.
The advantage for the theoretical and numerical treatment of the skin layer process of the plane interaction front is that we can proceed with a one-dimensional (1D) model in contrast to the numerical treatment of relativistic self-focusing in two or three dimensions (Jones et al., 1982; Pukhov & Meyer-ter-Vehn, 1996). One-dimensional numerical computations for laser intensities where only thermokinetic and no nonlinear forces are dominant were performed by Mulser (1970) including the reflected wave field and plasma with collisions. Inclusion of the nonlinear force but neglect of collisions (Lindl & Kaw, 1971) showed the action of the nonlinear force. Including the nonlinear force for plasma with collisions in the WAZER code (Shearer et al., 1970) but without reflection led to the discovery of the caviton and profile steepening. Using the Kinsinger code (Laboratory for Laser Energetics, University of Rochester) with reflection, with nonlinear forces and nonlinear collisions (Hora LLE, University of Rochester) from 1974, led to density rippling and self-generated phase reflection (see Hora, 1991, Figs. 10–11).
Extension to initially low reflectivity plasma densities (bi-Rayleigh profiles) showed the reduction of phase reflection for times up to a few picoseconds at neodymium glass laser intensities up to 1018 W/cm2, and the generation of deuterium plasma blocks of considerable thickness moving against the laser light with velocities exceeding 109 cm/s in the plasma corona, and blocks of similar velocities moving in the direction of the laser into the higher dense plasma interior. This block motion for laser interaction above 1015 W/cm2 was confirmed by applying the genuine two-fluid, 1D code (Lalousis et al., 1983) showing the very high longitudinal dynamic electric fields and generation of inverse double layers (Hora et al., 1984). Evaluating all these earlier results, the skin layer interaction could be concluded (Hora et al., 2002a).
For confirmation of these extraordinary facts, we performed measurements with a uniquely designed neodymium glass laser system where the optical conditions are fully identical for irradiation of the targets both for 0.5-ns and for 1.2-ps laser pulses of the same geometry and 0.7 J energy. The generation of megaelectron volt Au+30 ions was produced with a neodymium glass laser intensity of 2 × 1014 W/cm2 at 0.5-ns, and 8 × 1016 W/cm2 at 1.2-ps pulses. We further have comparisons with new measurements with longer laser pulse iodine lasers. These measurements clearly confirm that long laser pulses arrive at the very high maximum ion energies in agreement with relativistic self-focusing and nonlinear force acceleration, whereas the picosecond experiments with sufficiently suppressed prepulses are nearly without the plasma cloud in front of the target and permit only the skin layer interaction process. Nearly means that a 50-ps prepulse may have produced a plasma cloud of 5 to 10 μm thickness above the target, such that relativistic self-focusing (Fig. 1a; Hora, 1975; Osman et al., 1999; Hora, 2000a, 2000b) could be excluded but that the plane wave interaction in the skin layer scheme with a dielectric swelling (see Fig. 2) is producing blocks of plasma of nearly cutoff density (1021 cm−3) moving perpendicular to the target surface against the laser light and into the target interior (Fig. 3). A confirmation of the measured megaelectron volt Au+30 ions with a swelling S of about 3 and the experimentally determined electron quiver energy of 19 keV was shown (Hora et al., 2002b). The importance of the reduced prepulse was measured also in experiments with a varying prepulse (Zhang et al., 1998), where only a 70-ps-earlier prepulse produced the high X-ray emission in subpicosecond irradiated targets whereas the shorter (or vanishing) prepulses arrived at the lower X rays as expected from the skin layer model.

Example of the genuine two-fluid computation of the electromagnetic energy density (E2 + H2)/(8π) after one picosecond neodymium glass laser irradiation with an intensity of 1016 W/cm2 on a deuterium plasma of initially 100 eV temperature and an initial linearly increasing electron density from 50% of the critical density at the depth of zero from vacuum to the critical density at a depth of 12 μm showing a swelling of 3.5 for comparison with experiments.

Scheme of skin depth laser interaction where the nonlinear force accelerates a plasma block against the laser light and another block toward the target interior. In front of the blocks are electron clouds of the thickness of the effective Debye lengths of less than 500 nm.
We discuss now how the just described fast moving high-density blocks of deuterium plasma (or deuterium tritium plasma) are hitting cold DT plasma of solid state density and how a fusion reaction may be initiated at the front of the interface between the hot and the cold plasma. This is the essential mechanism of central spark ignition in the usual laser-produced plasmas at spherical irradiation by lasers. Reconstructing the most real conditions of spark ignition (Storm et al., 1988; Hora et al., 1998) we find that the high-temperature–low-density central spark fully follows the results of volume ignition (Hora et al., 1997, 1998) where the energy of 0.45 MJ in the core produces about 5 MJ fusion energy. This results in an energy density for triggering the spherical fusion detonation front into the cold and high-density outer core of
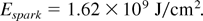
This is not very much different from the result (Hora, 1983; Hora et al., 1984) of interpenetration of nearly solid state density (space charge neutral) DT ions of 100 keV energy into solid state DT producing a fusion reaction wave (Hora, 1983) similar to a laser-driven flame (Bobin, 1971, 1974; Chu, 1972). The conditions of spark ignition are not fully comparable because of the volumetric distribution of the core reaction products and because of the higher than solid state density at the detonation front apart from radiation transport, so the results from the interpenetration for generation of a reaction front were similar to the value of Eq. (1). This value may be reduced, however, by up to a factor of about 50, if the corrected higher collision frequency due to the quantum effects (Hora, 1991, Sec. 2.6) and the reduction of the stopping power by collective effects (Gabor, 1953; Ray et al., 1976) and the double-layer-produced inhibition of thermal conduction are included (Hora, 1983). Without including this, a pessimistic result is the condition of Brueckner & Jorna (1974) for producing the ignition front into the cold plasma by the fast ions of the spark at
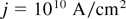
current density. In the case of the experimental results (Badziak et al., 1999, 2003), this condition (2) an easily be fulfilled by the plasma blocks of Figure 3, because DT densities of about 1021 cm−3 from the cutoff value are produced and if the laser intensity is a few times below the relativistic threshold, the optimum DT energy of 80 keV for the compressing plasma block arrives at ion velocities of 2.8 × 108 cm/s producing j ∼ 4 × 1010 A/cm2 in agreement with (2).
The recipe for using the nonlinear-force-driven plasma blocks from the skin layer interaction for fusion is simply explained:
For the condition 1 for using the prepulse-controlled nonlinear-force-driven plasma blocks from the plane skin layer process, this requires rather modest laser intensities of about 1018/λ2 W/cm2 (laser wavelength λ in microns). This simplifies the interaction conditions to defocusing and larger interaction areas, therefore arriving at an easier beam adjustment in reactors, as seen in Figure 4.

Focus diameter for producing DT ion energies εDT in the dense plasma blocks moving to the target interior when applying neodymium glass laser pulses of powers given by the parameters for an assumed swelling S = 3.
A necessary condition is that the laser pulse is not too short. Whatever phenomena will be produced, for the nonlinear force generation of the blocks for fusion one needs a minimum time of
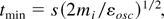
where s is the thickness of the main part of the (short) prepulse-produced plasma in front of the target for skin depth interaction. It is evident that for the ion mass mi for the DT case, and the resonance energy of the DT reaction, s has to be a few microns only. For higher εDT values, this condition is more relaxed.
From all this it should be realized that this possible preferred way to laser fusion is still only one of the numerous options (Atzeni, 2001; Vogel & Kochan, 2001) and only a beginning. The initiation was the Badziak et al. (1999) experiment that arrived at the intriguing view of the skin depth model (Badziak et al., 1999; Hora et al., 2002a, 2002b), which was connected to early numerical knowledge of the nonlinear-force produced picosecond push of dense plasma blocks (see Sect. 10.5 of Hora, 2000a). With respect to the prepulse control, a connection was given to the experiments of Zhang et al. (1998). The hard work was to repeat and extend the experiments with neodymium, iodine, and Ti-sapphire lasers (Zhang et al., 1998; Badziak et al., 1999; Hora et al., 2002a, 2002b), to get control of the prepulse as used (Badziak et al., 1999; Hora et al., 2002b) and perfectly verified (Zhang et al., 1998) and to merge these into conditions sketched by Figure 4 and Eq. (3). Extensive computations parallel to the measurements for better adjustment of the swelling and the reconstruction of density profiles for achieving results similar to that of Figure 2 have to be performed but with more realistic initial density and temperature profiles adjusted to experiments. How to develop this to an easily operated, modest cost petawatt–picosecond laser fusion power station following the basic concept (Tabak et al., 1993) and a large number of future developments in fusion and the petawatt–picosecond lasers to be derived from these new views is then a higher task of management and politics.
Because all this is based on the CPA-produced petawatt–picosecond laser pulses, it is a simplifying step beyond the fast ignitor scheme (Tabak et al., 1993) that was proposed to add heating to the laser-compressed plasma of up to 2000 times the solid density but of too low temperature (Azechi et al., 1991). The difficulties with this scheme were measured (Fews et al., 1994) and are theoretically expected especially with respect to the hole boring (Hora et al., 2002c) into the high-density compressed plasma and all the relativistic interaction effects. One way out with the new nonlinear-force block-ignition scheme is to avoid any precompression and to work just below or near the relativistic threshold. The crucial importance of the fast ignitor is that it initiated the development of the petawatt–picosecond laser pulses (Perry & Mourou, 1994).
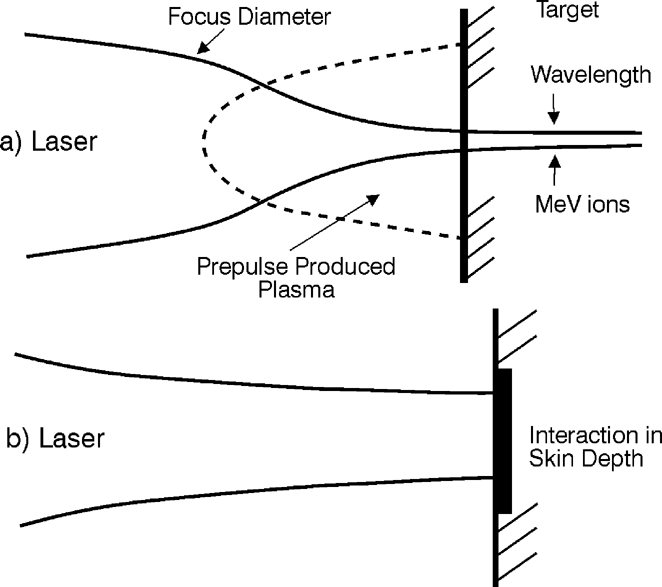
Scheme of laser–plasma interaction with relativistic self-focusing (Hora, 1975; Osman et al., 1999; Hora, 2000a, 2000b) (a) where the long irradiation produced a plasma cloud above the target permitting (relativistic) self-focusing in contrast to the plane wave interaction in the skin layer scheme and (b) without the plasma for self-focusing but with plane geometry acceleration of the laser-irradiated electron cloud following the nonlinear (ponderomotive) force.

Example of the genuine two-fluid computation of the electromagnetic energy density (E2 + H2)/(8π) after one picosecond neodymium glass laser irradiation with an intensity of 1016 W/cm2 on a deuterium plasma of initially 100 eV temperature and an initial linearly increasing electron density from 50% of the critical density at the depth of zero from vacuum to the critical density at a depth of 12 μm showing a swelling of 3.5 for comparison with experiments.

Scheme of skin depth laser interaction where the nonlinear force accelerates a plasma block against the laser light and another block toward the target interior. In front of the blocks are electron clouds of the thickness of the effective Debye lengths of less than 500 nm.

Focus diameter for producing DT ion energies εDT in the dense plasma blocks moving to the target interior when applying neodymium glass laser pulses of powers given by the parameters for an assumed swelling S = 3.