INTRODUCTION
The process of laser ablation of low- and medium-Z targets is fundamental for laser-driven inertial confinement fusion (ICF) since it is the source of the driving pressure in ablative compression of fusion targets. Moreover, laser ablation has a wide range of applications (Bashir et al., Reference Bashir, Rafique and Ul-Haq2007, Bussoli et al., Reference Bussoli, Batani, Desai, Canova, Milani, Trtica, Gakovic and Krousky2007, Fang & Ahmad, Reference Fang and Ahmad2007, Thareja & Sharma, Reference Thareja and Sharma2006, Veiko et al., Reference Veiko, Shakhno, Smirnov, Miaskovski and Nikishin2006 Wang et al., Reference Wang, Xu, Zhou, Chu and Fu2007). For this reason, very many studies of mass ablation rate and of the generation of ablation pressures have been carried out over the past 20 years. Despite this, there are still some good reasons to study the process of laser ablation today: (1) First, progress in laser technology and in laser smoothing techniques allow the realization of cleaner experiments. Most of past studies were done by focusing on small focal spots in order to achieve intensities ≥1013 W/cm2. Thereby, results were affected by two-dimensional (2D) effects (lateral transport of thermal energy, lateral flow of mass).
Even when large spots were used, these were not optically smoothed (the first smoothing technique, random phase plates, was introduced in the 1980s (Kato et al., Reference Kato, Mima, Miyanaga, Arinaga, Kitagawa, Nakatsuka and Yamanaka1984) and were then characterized by “hot spots.” The measured ablation rate was therefore dominated by the effect connected to the short-scale nonhomogeneities.
Moreover, the use of phase zone plate optical smoothing (Stevenson et al., Reference Stevenson1994; Koenig et al., Reference Koenig, Faral, Boudenne, Batani, Bossi and Benuzzi1994; Batani et al., Reference Batani, Bossi, Benuzzi, Koenig, Faral, Boudenne, Grandjouan, Temporal and Atzeni1996, Reference Batani, Bleu and Lower2002) (see next section) allows a flat-top intensity distribution to be produced. This is important since the ablation parameters in the central flat region of the focal spot can be directly compared to analytical results obtained from one-dimensional (1D) models, which by definition assume a spatially uniform intensity. (1) At the shortest laser wavelengths, there is still some incertitude concerning the scaling versus laser intensity. For instance, measurements at 0.351 µm (Key et al., Reference Key, Toner, Goldsack, Kilkenny, Veats, Cunningham and Lewis1983, Reference Key1979) showed a scaling ≈ I0.3, very different from what is predicted by theoretical models (usually ≈ I0.7). Such experimental results were dominated by 2D and hot spots effects. This is important because shorter laser wavelengths (third and fourth harmonics of Nd, as well as other wavelengths from gas lasers) give higher ablation rate and pressure, and are thereby envisaged as future drivers for ICF direct drive experiment (Koenig et al., Reference Koenig, Fabre, Malka, Michard, Hammerling, Batani, Boudenne, Garconnet and Fews1992; Lindl, Reference Lindl1995). Also, this allows studying material characteristics (Fortov et al., Reference Fortov, Kilpio, Krasyuk, Batani, Lomonosov, Pashinin, Shashkov, Semenov and Vovchenko2002) and plasma characteristics (Batani et al., Reference Batani, Benuzzi, Koenig, Krasyuk, Pashinin, Semenov, Lomonosov and Fortov1999, Reference Batani, Dezulian, Redaelli, Benocci, Stabile, Canova, Desai, Lucchini, Krousky, Masek, Pfeifer, Skala, Dudzak, Rus, Ullschmied, Malka, Faure, Koenig, Limpouch, Nazarov, Pepler, Nagai, Norimatsu and Nishimura2007). (3) Finally, still some details are not clear in the literature concerning the very mechanism of laser ablation. For instance, even recent important reviews (Lindl, Reference Lindl1995) report the scaling law:
where I is the laser intensity on target in W/cm2, λ is the laser wavelength in µm, and A and Z are the mass number and the atomic number of the target. This is obtained if laser light is absorbed at the plasma critical layer.
In reality, the scaling should also include time dependence. The plasma corona becomes larger during the interaction, and the distance between the absorption region and the ablation surface (n e ≈ solid material) increases with time. This brings to a decoupling of the laser beam from the target and, as a result, the mass ablation rate decreases with time. In particular, it is found that the shock pressure is related to laser and target parameters (Mora, Reference Mora1982).
where the time t is in ns. As in Eq. (1), pressure strongly depends on laser parameters and only weakly on the material. The decrease in time of pressure, even for constant laser irradiation, has been first described by Caruso and Gratton (Reference Caruso and Gratton1968) and Mora (Reference Mora1982). The difference between de-localized absorption and localized (at critical density) models is discussed elsewhere (Gus'kov, Reference Gus'kov, Rozanov and Zverev1983; Meyer & Thiell, Reference Meyer and Thiell1984; Limpouch, Reference Limpouch, Lebo and Rozanov1987).
In order to address questions (1), (2), and (3), an experiment was recently performed at the PALS laboratory, using irradiation at λ = 0.44 µm (Batani et al., Reference Batani, Stabile, Ravasio, Desai, Lucchini, Ullschmied, Krousky, Skala, Kralikova, Pfeifer, Kadlec, Mocek, Prag, Nishimura, Ochi and Zvorykin2003a). Results showed a scaling versus laser intensity quite close to the theoretical prediction and also gave some evidence for the mechanism of delocalized absorption.
Experimental details have been analyzed (Batani et al., Reference Batani, Stabile, Ravasio, Desai, Lucchini, Ullschmied, Krousky, Skala, Kralikova, Pfeifer, Kadlec, Mocek, Prag, Nishimura, Ochi and Zvorykin2003a, Reference Batani, Stabile, Ravasio, Desai, Lucchini, Desai, Ullschmied, Krousky, Juha, Skala, Kralikova, Pfeifer, Kadlec, Mocek, Präg, Nishimura and Ochi2003b). However, one question, which remained partially opened, was the possibility of 2D effects partially affecting the measurement of shock velocity in that experiment. The goal of this paper is therefore to support experimental results with 2D numerical hydrodynamical simulations performed with the code “ATLANT” (Lebo, Reference Lebo, Popov, Tishkin and Rozanov1994, Reference Lebo, Demchenko, Iskakov, Limpouch, Rozanov and Tishkin2004) and derive more detail scaling for future experiments.
EXPERIMENTAL SETUP AND RESULTS
The experiment was performed with the iodine laser of PALS (Jungwirth, Reference Jungwirth2005; Batani et al., Reference Batani, Dezulian, Redaelli, Benocci, Stabile, Canova, Desai, Lucchini, Krousky, Masek, Pfeifer, Skala, Dudzak, Rus, Ullschmied, Malka, Faure, Koenig, Limpouch, Nazarov, Pepler, Nagai, Norimatsu and Nishimura2007), which delivers a single beam, 29 cm in diameter, with typical energy of 250 J per pulse at 0.44 µm (Jungwirth et al., Reference Jungwirth, Cejnarova, Juha, Kralikova, Krasa, Krousky, Krupickova, Laska, Masek, Mocek, Pfeifer, Prag, Renner, Rohlena, Rus, Skala, Straka and Ullschmied2001). The laser pulse is Gaussian in time with a full width at half maximum (FWHM) of about 400 ps.
The focusing lens had a focal length f = 600 mm (f/2 aperture). A blue filter before the entrance window did cut ω and 2ω light. The diagnostics used to detect the shock breakout from the target rear face consisted in a pair of lenses imaging the rear face onto the slit of a streak camera (Hamamatsu C7700 with S-1 photocathode). The first one was a complex f/2 objective, with f = 100 mm, producing a parallel beam between the two lenses. The second lens had f = 98 cm, giving a total optical magnification M = 9.8.
Stepped targets were made of bulk Al by lathe matching. The base was ≈8 µm, and the step thickness was ≈8.5 µm. Al was chosen because its behavior at high pressure is well known, making it a typical reference material for laser-shock experiments.
The primary condition of producing high quality flat shocks imposed the use of phase zone plates (PZP). Since, for technical reasons, it was not possible to produce a PZP with the full size of the laser beam, we designed a smaller PZP to be placed at f/2 from the target. The design of our optical system (PZP + focusing lens) implied a focal spot of 400 µm FWHM, with a 250 µm flat region in the center, corresponding to intensities up to 2 × 1014 W/cm2.
Figure 1 shows a streak image of shock breakout from planar and stepped Al targets. The first image shows that a rather flat shock front has been created. The second image allows measuring the time delay between the breakout at the base and at the step, giving the average shock velocity in the step. From shock velocity we determine the shock pressure using the Hugoniot data for Al from the SESAME tables (T4 Group LANL, 1983). Such shock pressure is the pressure produced by the laser beam on the irradiated side, i.e., the ablation pressure.

Fig. 1. (Color online) Left: shock breakout from a flat aluminum target. Right: Shock breakout image from an Al target for laser energy E L = 108 J. The dimensions of the images are 1.69 ns × 1300 µm. Time flows up to down. Velocity of shock wave can be obtained as D = d 2/(t2 − t 1). Here the time delay between base and step is Δt = (t 2 − t 1) = 267 ps giving a shock velocity D = 31.84 µm/ns.
The method works if the shock is stationary, and we designed the targets to get a stationary shock in the step. This can be addressed by using hydrodynamics simulations or analytical models (Batani et al., Reference Batani, Balducci, Nazarov, Löwer, Koenig, Faral, Benuzzi and Temporal2001, Reference Batani, Löwer, Hall, Benuzzi and Koenig2003c), which approximates the Gaussian with a trapezoidal time shape, and again was checked by using the code “ATLANT.”
SIMULATION CODE
We used the 2D hydrodynamic Lagrangian code “ATLANT” in cylindrical geometry (with coordinates R, z, t). Below we list the set of basic equations, which have been solved numerically with help of different methods (see in details in Lebo & Tishkin, Reference Lebo and Tishkin2006).
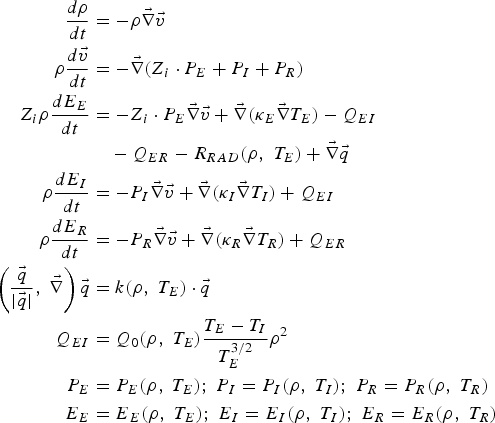
Here ρ is the density, ν is the velocity; E E, E I, E R are the specific (i.e., per units of volume) internal energy of electrons, ions, and photons; P E, P I, P R, T E, T I, T R are the electron, ion, radiation pressures, and temperature; R RAD represents the radiation losses of plasma; ![]() is the laser-radiation flux; κE, κI, κR are the coefficients of thermal conductivity for the electron, ion, and radiation plasma components; Z i is the mean degree of ionization in the Lagrange cell; k-is the absorption factor of laser radiation. Finally the following equations
is the laser-radiation flux; κE, κI, κR are the coefficients of thermal conductivity for the electron, ion, and radiation plasma components; Z i is the mean degree of ionization in the Lagrange cell; k-is the absorption factor of laser radiation. Finally the following equations
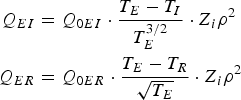
give, respectively, the rate of electron-ion energy exchange in the Landau-Spitzer approximation, and the rate of electron-photon energy exchange, which is determined by the bremsstrahlung processes.
In our simulations, we have used a library for state equations based on the quotidian equations of state model (QEOS) (More et al., Reference More1988). It consisted of three parts: (1) Electron ionization-equilibrium equation of state based on Thomas-Fermi statistical model with scaling property for atomic number and atomic weight. (2) Analytical ion equation of state that combines Debye, Gruneisen, Lindemann and fluid-scaling laws. (3) Empirical term, which introduces correction for chemical bonding, and is derived from physical properties of a given material.
No radiation transport has been used in the simulation because we expect that this (and in particular, X-ray preheating) is negligible in our case, due to the sufficiently low laser intensity and to the use of a CH ablator before the Al layer.
SIMULATION RESULTS AND COMPARISON WITH EXPERIMENTAL DATA
We have performed several sets of simulations in order to reproduce the experimental results on measurement of shock wave velocity in stepped targets. In our simulations, we have varied the absorbed laser energy (E Lasabs) from 50 to 200 J and the shape of the laser intensity profile (“Flat-top” or “Gauss”) while keeping constant the laser wavelength (3ω, λ = 0.438 µm) and pulse duration. For simplicity, the temporal shape of the pulse was taken triangular, beginning at the time t = 0, having its maximum at t = 400 ps, and ending at τ = 800 ps.
We have simulated the irradiation of three-layered disks: CH layer (dCH = 2 µm), first Al layer (d1_Al = 8 µm) and second Al layer (d2_Al = 8.5 µm). Figure 2 shows the initial Lagrangian mesh, 0 < R < R 0. On borders of the simulated area (R 0 = 200 µm) elastic and thermal isolated walls boundary conditions have been set. In order to avoid unnecessary numerical problems around the step edge, the base/step profile has been “smoothed” by assuming a sinusoidal profile (over a typical half of wavelength of λp = 20 µm), as it is clear from Figure 2.

Fig. 2. Left: initial Lagrange mesh used in the ATLANT-code simulation (cylindrical symmetry around the Z axis is assumed), Right: scheme of the simulation.
The maximum laser intensity is I max = 2E lasabs/πR F2τ, where R F is the radius of the focal spot. first case (R 0 = 200 µm, absorbed energy 100 J): we first present the results of simulations with R F = R 0 = 200 µm, and a “flat-top” laser flux profile.
Figures 3a and 3b shows the situation at the time when the shock reaches the rear side of the base, and at the time when it reaches the rear side of the step (notice the plasma corona expansion in the region Z > 0 and the part of the target which has been ablated). The simulation has been performed for a laser absorbed energy of 100 J, the shock reaches the rear side of the base t 1 = 0.3257 ns and it reaches the rear side of the step at t 2 = 0.555 ns. This gives a shock wave velocity D = d 2/(t 2 − t 1) = 8.5 µm/(0.555 ns – 0.3257 ns) = 37.07 km/s.

Fig. 3. The contours of target density at the time: (a) t = 0.35 ns (just after the shock reaches the rear of the base) and (b) t = 0.55 ns (just before it reaches the rear of the step). E Lasabs = 100 J. The laser beam comes from top of figure.
We have also made 1D calculation with help of “ATLANT” code to study if 2D geometry affects the shock wave velocity. The target consisted of two layers: outer CH layer with initial thickness 2 µm (0 < Z < 2 µm) and Al layer with thickness 16.5 µm (−16.5 µm < z < 0). The shock wave first reaches the CH-layer and part of the second layer with thickness 8 µm at the moment t 1 = 0.328 ns and reached the rear side of target at the moment t 2 = 0.5576 ns. These results are close to the 2D ones (with stepped targets). Figure 4 illustrates the density and pressure profiles at the time moments t = 0.3226 ns (1) and t = 0.5576 ns (2b). From these simulations, it follows that the transverse motion does not influence the measurement of shock wave velocity in condense matter and that D = 37.1 km/s too.

Fig. 4. Density and pressure profiles at t 1 = 0.3226 ns (shock front has reached the base-step interface at Z = −8 µm) (a) and t 2 = 0.5576 ns (shock front has reached the rear side at Z = −16.6 µm) (b) in 1D simulation. E Lasabs = 100 J.
Second case (R 0 = 200 µm, absorbed energy 68 J): Figures 5a to 5d illustrate the density and pressure profiles in the z-direction at R = 0 (step) and at R = 197.5 µm (base). In this case, the shock wave reaches the first boundary t 1 = 0.37 ns and the second boundary at t 2 = 0.619 ns. Figure 5 shows the density profile (1) and the pressure profile (2) at t 1 = 0.4 ns, just after the shock wave has come to the rear side of the base; and the density (3), and pressure (4) profiles at t 2 = 0.65 ns just after it has reached the rear of the step, and the right part of target is unloaded.

Fig. 5. 2D simulations: density (a) and pressure (b) profiles at t = 0.4 ns (0.03 ns after shock breakout at the base); density (c) and pressure (d) profiles at t 2 = 0.65 ns (0.03 ns after shock break out at the step); E Lasabs = 68 J. (1) profile at R = 0 (Z axis), and (2) at R = 197.5 µm.
Third case (R 0 = 100 µm, laser intensity 4 × 1014 W/cm2): The distance, which the shock wave travels in condense matter is much less then the transverse scale of target R 0 and mainly depends on laser intensity. In another simulation, we have diminished R0 by two times and used I max = 4 × 1014 W/cm2. Figure 6 illustrates the motion of shock wave in the target. In this case, we got D = 44 km/s.

Fig. 6. Maximal laser intensity I max = 4 × 1014 W/cm2: the shock wave reaches the rear side of the base at t 1 = 0.274 ns and the step at t 2 = 0.467 ns. The case (a) shows the situation at t = 0.3 ns, and the case (b) at t = 0.5 ns.
DISCUSSION
Figure 7 illustrates the results of a set of numerical simulations for the different values of I max. We have compared the numerical results of shock wave velocities with experimental data. The “crosses” are the experimental data, the solid line is the results of simulations. In our simulations, we assumed a 100% absorption of laser energy. In the real experiment, part of the energy was lost as a result of the use of PZPs, of partial absorption of the e.m. wave in the plasma and of (2D) refraction effects in the plasma corona. As a result, we expect simulation results to be an upper limit to the experimental data, as it is indeed the case in Figure 7. We have supposed that about 30% of laser energy was lost.

Fig. 7. Shock velocity vs. incident laser intensity, markers (I): experimental points after (Batani et al. Reference Batani, Stabile, Ravasio, Desai, Lucchini, Ullschmied, Krousky, Skala, Kralikova, Pfeifer, Kadlec, Mocek, Prag, Nishimura, Ochi and Zvorykin2003a), continuous line with markers (■): simulation results, dashed line with markers (•), – corrected results with take into account the losses of laser energy.
In a second series of calculations, we studied the issue of conformity of data “scaling: to Eqs. (1) and (2). For this purpose, we simulated the interaction of laser light with an Al layer with initial thicknesses d = 20–60 µm without step profile with a flat-top laser profile with radius 200 µm. Thus, 2D effects were not considered.
The temporal shape of the laser pulse was an isosceles triangle reaching zero at times t 1 = 0 ns and t 3 = 0.8 ns with maximum at t 2 = 0.4 ns. In the calculations, the effects of laser beam refraction and reflection were not considered, and again we assumed 100% absorption of laser radiation in plasma. The profiles of pressure and density along the Z axis at the different time moments comes from our calculations. The maximum of pressure value has been increased up to t = 0.4 ns.
In this series of simulations, in addition to the QEOS model, we also used the equation of a state (EOS) proposed in Zel'dovich and Raizer (Reference Zel'dovich and Raizer1967) and Afanas'ev et al. (Reference Afanas'ev, Gamaly, Rozanov and Trudi1982), which considers two terms in the equation of ionic pressure: the thermal and the elastic factor, which calculates the ionization kinetics with an average ion approach in each Lagrangian cell. This is described by the following sets of equations
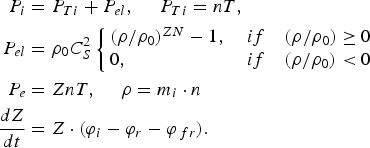
Here ρ and n are the density and ion concentration in condense matter, Z is the average ion charge in the Lagrangian cell, ϕi, ϕr, and ϕfr are the rates of three particle ionization, three particle-recombination and photo-recombination, and ρ0 and C s are the initial density and sound velocity in condense matter in normal conditions.
Calculations have been made for various values of laser intensity (I max) at a fixed wavelength λ = 0,438 µm (see Table 1). From numerical calculations it is possible to derive the following scaling which is valid for the case λ = 0.438 µm.
Table 1. Maximum pressure in the case λ = 0.438 μm t = 0,4 ns versus laser intensity. Second line: numerical calculations using the QEOS model; third line: numerical calculations using the RZI model; fourth line: analytical scaling using Eq. (2)


This shows a power dependence on laser intensity, which is quite close to the that of Eq. (2), the exponent being 0.83 instead of 0.75 (the difference with the exponent in Eq. (1), which is 0.67 is far more pronounced).
Figure 8 illustrates the results contained in Table 1 showing the results of numerical calculations of maximum pressure (Pmax) versus intensity at the fixed wavelength of laser radiation λ = 0.438 µm (3ω).

Fig. 8. Dependence of pressure on maximum laser intensity at λ = 0.438 µm and at t = 0.4 ns.
In the case of the Zel'dovich and Raizer (Reference Zel'dovich and Raizer1967) model with ionization kinetics (ZRI-model), the dependence of Pmax from I max differs on the results obtained with the QEOS model (see Table 1). But the differences are not large, and it is very difficult to discriminate between the two models in experiments.
Figure 9a shows the shock wave propagation in the Al layer along the Z axis as a function of time for the case of QEOS model. Figure 9b shows the shock wave propagation for the case of the RZI model. Calculations are made for the maximal intensity of laser radiation I max = 1.99 × 1014 W/cm2, wavelength of radiation λ = 0.438 µm and d = 60 µm. Here the pressure is represented as a function of the Lagrangian coordinate XMS, which is simply the sum of the quantities Δ M ij, i.e., the mass of the Lagrangian cells in the simulation mesh.

Fig. 9. The pressure distribution in the matter as function of mass cords for different time moments: t 1 = 0.2 ns, t 2 = 0.4 ns, t 3 = 0.8 ns (a) QEOS; (b) Zel'dovich and Raizer's EOS model.
The pressure and shock wave velocities in both models are approximately the same. For example, at t = 0.8 ns the maximum pressure is Pmax = 23.5 Mbar for XMS = 0.52 × 10−6 arb. units in the case of QEOS model, and Pmax = 22.0 Mbar for XMS = 0,51 × 10−6 arbitrary units in the case of the ZRI model (see Fig. 9).The pressure profile is not monotonous in case (b): this is the effect of numerical approximations. In principle, it is possible to solve this problem by decreasing the time step in the calculations. The distributions of temperature and ion charges in condense matter differ some more in the QEOS and ZRI models. Figure 10 illustrates the ion charge distribution in both cases.
Figure 11 shows the evolution of the absorbed laser power as a function of distance (Z) for different times. The plotted quantity is (P abs/DM) = (P in − P out)/DM, where P in and P out are the input and output laser power in each Lagrangian cell, and DM the mass of the Lagrangian cell. In this case, the intensity of laser radiation was I max = 1.99 × 1014 W/cm2 and the radiation wavelength λ = 0.438 µm. The calculation shows that radiation is non-uniformly absorbed in the plasma corona, and shock wave pressure varies in time and space.

Fig. 10. Average charge of ions (FQ) as function of Lagrangian coordinates (XMS) for QEOS (a) and ZRI (b) models for different times. I max = 1.49 × 1014 W/cm2, λ = 0.438 µm.

Fig. 11. Laser absorbed power per mass units (Pabs/DM) as function of distance (Z) for different times. I max = 1.99 × 1014 W/cm2, λ = 0.438 µm.
In addition, since Eq. (2) shows the dependence of pressure from time, we have also performed a set of 1D simulation to observe the dependence of Pmax from laser pulse duration. Results are shown in Table 2. The laser pulse duration is τ = t 3 = 8 ns (maximal intensity at t 2 = 4 ns), or, as before, t 3 = 0.8 ns. The range of laser intensities I max = 1013 – 5 × 1014 W/cm2, and the other parameters λ = 0.438 µm and d = 200 µm.
Table 2. Comparison of two sets of numerical simulations with and t3 = 8 ns and t3 = 0.8 ns and the scaling for Ps given by Eq. (3). Range of laser intensities Imax = 1013 − 5 × 1014 W/cm2, λ = 0.438 µm, and d = 200 µm

Using such results, we can improve our Eq. (6) as:

The scaling time seems quite different from Eq. (2). However this should not be a surprise since this is the result of simulations done with varying laser intensity and for different pulse duration τ. So the physical meaning is different from Eq. (2), which shows the scaling versus time. In order to show the time dependence explicitly, we have performed a simulation using the 1D version of the code ATLANT and followed the evolution of maximum shock pressure. Results are shown in Figure 12 for laser pulse energy of 804 J and duration of 0.8 ns (flat-top temporal shape) and an Al target with thickness 60 µm.

Fig. 12. (Color online) Evolution of maximum shock pressure for a laser pulse energy of 804 J, a duration of 0.8 ns (flat-top temporal shape) and an Al target with thickness 60 µm. The radius of the focal spot (used in the calculation of the laser intensity) was 200 µm. (points and solid line) and interpolation using the power law dependence of Eq. (2).
We see that after an initial “creation” phase, shock pressure decays with time exactly as predicted by Eq. (2). We think that both these results and those presented in Figure 11, as well as the previous scaling versus laser pulse duration τ, give evidence of delocalized absorption of laser energy.
Finally we have used our simulation results to study the relation between the shock pressure (P0) and the shock velocities (D). Classically these are related by Hugoniot equations:
where P0 and ρo are the initial pressure and density and γ the adiabatic index. For strong shocks, as it is practically our case, this equation simplifies to
Table 3 shows the relation between the laser intensity (I max in units of 1014 W/cm2), the pressure (PS in Mbar), and the shock velocities for γ = 5/3 (D 1) and γ = 2 (D 2), and the experimental results (D exp in km/s) (see Fig. 7). It should be noticed that laser intensity and pressure increase up to 0.4 ns and then decrease, so shock velocity varies during the laser pulse. D1(2) follows the maximum value of shock wave pressure.
Table 3. Shock pressure data derived from simulations (Mbar), shock velocity data calculated using Eq. (4) with γ = 5/3 (D 1) and γ = 2 (D 2), and experimental results (in km/s) for shock velocity

Let's finally notice that 2D simulations have allowed predicting laser energy losses due to reflection and refraction of the laser beam in the extended plasma corona. In some cases, these can be as high as 30%. Also the pressure behind the shock front in 2D simulations with a radial profile of laser intensity tends to an asymptotic value, which is given by 1D simulations, as the width of the shock front (laser profile) is increased.
CONCLUSIONS
In this paper, we have analyzed the results of a recent experiment performed at the PALS laboratory concerning ablation pressure at 0.44 µm at irradiance up to 2 × 1014 W/cm2, using the code “ATLANT.” 2D hydrodynamics simulations have shown that 2D effects did not affect the experimental measurements of shock velocity in the conditions of “PALS” installation experiments. We have derived some scaling, which could be useful for future experiments. About 30% of laser energy was lost in the results of reflection and refraction effects. Also they allowed us to see that the shock is reasonably stationary in the step and finally give evidence of the phenomenon of delocalized absorption of laser light.
Acknowledgements
We thank all the PALS team (J. Ullschmied, J. Skala, B. Kralikova, M. Pfeifer, Ch. Kadlec, T. Mocek, and A. Präg) and C. Danson and D. Pepler from the Rutherford Appleton Laboratory, UK for the PZP.

















