Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-06T07:39:41.782Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulations of energetic proton emission in laser–plasma interaction

Published online by Cambridge University Press:  25 March 2004

LAURENT POMMIER  and
ERIK LEFEBVRE
LAURENT POMMIER
Affiliation:
Département de Physique Théorique et Appliquée, Commissariat à l'Energie Atomique/Direction des Applications Militaires Ile de France, Bruyères-le-Châtel, France
ERIK LEFEBVRE
Affiliation:
Département de Physique Théorique et Appliquée, Commissariat à l'Energie Atomique/Direction des Applications Militaires Ile de France, Bruyères-le-Châtel, France
Rights & Permissions [Opens in a new window]

Abstract

Energetic protons are emitted from thin foils irradiated by short laser pulses at high intensities. One- and two-dimensional particle-in-cell simulations have been used to study the influence of initial proton position, laser irradiance, and target density profile on this ion acceleration. These simulations bring additional support to the idea that protons are mainly accelerated from the rear side of the target, by electrostatic fields associated with hot electrons escaping into vacuum. The density scale length at the front of the target appears to be the main parameter to increase proton energies when the laser irradiance is fixed.

Keywords

Energetic protonsHot electron productionLaser–plasma interactionNumerical simulationsUltraintense laser pulses
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 4 , October 2003 , pp. 573 - 581
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

Technological advances in the amplification and compression of chirped laser pulses have fueled the race toward higher laser intensities, and now make it possible to study matter under irradiances of 1019 W/cm2 and more in many laboratories worldwide. The very energetic plasmas produced by this irradiation are interesting sources of relativistic electrons (Malka & Miquel, 1996; Key et al., 1998), hard X rays (Key et al., 1998), neutrons (Key et al., 1998; Disdier et al., 1999), and energetic ions (Fews et al., 1994; Clark et al., 2000a, 2000b; Hatchett et al., 2000; Maksimchuk et al., 2000; Snavely et al., 2000; Hegelich et al., 2002). The relativistic and kinetic effects associated with this strong-field interaction also mean that theoretical models of these phenomena can be difficult to derive, and much insight can be gained by numerical simulations.

The production of energetic protons by high-intensity laser–plasma interaction has recently received a renewed interest, even though first observations and experimental evidences on this subject date back to the Los Alamos Helios program (Gitomer et al., 1986). In experiments with high Iλ2 (above 1015 Wμm2/cm2) made possible by CO2 lasers, a fast ion signal was diagnosed. It was made only of protons, regardless of the target composition, and was attributed to hydrogenated contamination at the target surface. More recently, another study (Fews et al., 1994) on the VULCAN laser, at the Rutherford Appleton Laboratory, concluded that 10% of the laser energy was transferred into ion kinetic energy. Other experiments showed that 1-ps, 1.053-μm wavelength laser pulses irradiating 125-μm-thick aluminum foils at 5 × 1019 W/cm2 would accelerate 1012 protons up to an energy of 17.6 MeV, as well as other, heavier ions (Clark et al., 2000a, 2000b). At the Lawrence Livermore National Laboratory (Hatchett et al., 2000; Snavely et al., 2000), experiments with the Petawatt laser focused on 100-μm-thick plastic foils at 3 × 1020 W/cm2 produced 3.5 × 1013 protons with energies up to 58 MeV. Other experiments at lower intensities (I ≈ 3 × 1018 W/cm2; Maksimchuk et al., 2000) concluded that the proton maximum energy was proportional to Iα, with α between 0.3 and 0.4.

At these intensities, ions are not directly accelerated by the laser ponderomotive force, but instead by electrostatic fields created by electron acceleration and the resulting electric charge imbalance. Yet the origin of these energetic ions is somewhat controversial. Some groups claim that they originate from the front (laser-irradiated) side of the target, where they are dragged into the target by the hot laser-accelerated electrons. This is a variation on hole boring (Wilks et al., 1992) and electrostatic shocks (Denavit, 1992), which were evidenced 10 years ago in numerical simulations. Other groups claim that ion acceleration occurs on the rear side of the target, under the influence of strong sheath electrostatic fields created by hot electrons leaving the target. This scenario also has been validated by numerical simulations showing that ions could be accelerated from the target rear side (Pukhov, 2001; Wilks et al., 2001). In addition, both opinions are supported by some experimental evidence: activation (Maksimchuk et al., 2000) and ion collimation measurements (Clark et al., 2000a) for the “front side” model and directionality of the ion beam (Hatchett et al., 2000) and sensitivity to the rear side density gradient (Mackinnon et al., 2001) for the “rear side” model.

Numerical simulation so far has focused on model, isolated cases. In this article we will discuss the influence of different physical parameters on the proton emission during high-intensity interactions, with a number of simulation results obtained with the relativistic particle-in-cell (PIC) code Calder, run in one- and two-dimensional (1D and 2D) geometry. In the first section, we use 1D simulations to illustrate the competition between front- and rear-side acceleration, and show that the latter is dominant in most experimental situations today. We then study how proton energies evolve according to time, laser irradiance, target width, and scale length at the back of the target. In the last section, we use 2D simulations to show that the scale length at the front of the target, due to a laser prepulse, is an influent parameter to increase proton energies. The energies and trends that we observe in this case are in good agreement with experiments (Maksimchuk et al., 2000). We believe that collisionless PIC simulations, as presented here and, for example, in Pukhov (2001) and Wilks et al. (2001), can capture most of the physics involved in ion acceleration. One-dimensional simulations do not include transverse effects, thus preventing quantitative comparison to experiments, but they are nonetheless very useful to study the target “Coulomb explosion” over long times and with low numerical noise. Inclusion of collisions would not change the general picture, as we are dealing with very thin targets and very hot electrons, which lose their energy to ions through collective fields much more rapidly than they would through collisions. We believe that hydrogen is very rapidly field ionized by the laser (at the front surface) or the electrostatic field (at the back surface), justifying that we start our simulations with preionized hydrogen layers. This point would need more refinement if we were interested in the acceleration of heavier ions (Zhidkov & Sasaki, 2000; Hegelich et al., 2002).

2. ONE-DIMENSIONAL SIMULATIONS

2.1. Origin of the proton emission

The origin of the proton beam, from the front or back side of the target, has been much debated recently, with contradictory experimental evidence (Clark et al., 2000a, 2000b; Hatchett et al., 2000; Maksimchuk et al., 2000; Snavely et al., 2000). To clarify this issue, we performed some 1D simulations of a thin overdense (2.5 nc, where nc is the critical density associated with the laser frequency) Al slab covered with hydrogen on both sides and irradiated at normal incidence by a 2 × 1018-W/cm2, 1-μm-wavelength, and 530-fs-duration laser pulse. The hydrogen layer at the back (nonirradiated) surface is 0.03 μm thick, at 2.5 nc. In most experiments to date, the front (laser-irradiated) surface of the target is slightly heated by amplified spontaneous emission (ASE) preceding the main laser pulse. This drives a moderate plasma expansion, with typical density gradients ne /(dne /dx) of a few micrometers. We included this density profile in our calculation by assuming an exponential ramp with gradient L = 1 μm from ne /nc = 2.5 × 10−3 to ne /nc = 2.5. The proton layer at the front is then spread over the first 3.5 μm of the density profile, resulting in the same areal density as at the back surface. Figure 1a illustrates this initial state of the target. At the end of the laser pulse, 8% of the incident energy has been absorbed into the target, essentially coupled to a hot electron population with an average temperature of 450 keV. These hot electrons spread around the target, creating an ambipolar field at both sides (Fig. 1b) and driving the proton expansion, as already described (Pukhov, 2001; Wilks et al., 2001). Five picoseconds after the beginning of the interaction, the system has relaxed to a point where almost all the absorbed energy has been transferred to the ions. The front-surface protons have been accelerated toward the laser to a maximum energy of 6.3 MeV, whereas those initially sitting at the rear surface have been accelerated up to 9.2 MeV along the incident laser direction (Fig. 1c,d). This more-or-less symmetric blow-off of the plasma is consistent with a scenario in which the laser ponderomotive pressure is of little importance. The proton distributions display high and low energy cutoffs. The high-energy one is consistently observed in experiments. The low-energy cutoff is related to the proton layer thickness: As protons feel lower accelerating fields when they are deeper in the proton layer, the low-energy edge of the spectrum corresponds to the energy of the innermost proton. Diminishing the layer thickness might, hence, offer a way to reduce the energy spread of the protons, albeit at the expense of coupling efficiency. This effect could also help explain the observation of “proton rings” made, for example, in Clark et al. (2000a).

Initial density profile (a), electrostatic field at 1.1 ps (b), density profile (c), and proton distribution functions (d) at 5.3 ps. The target is an aluminum foil covered with two proton layers at the front (dark grey) and back (light grey), with an exponential density profile at the front. It is irradiated by a 530-fs, 2 × 1018-W/cm2 pulse at 1-μm wavelength.

Some differences appear when one considers a target that has not expanded prior to the interaction. In this case, the protons at the front surface can be accelerated forward by the laser ponderomotive pressure, as they are located close to the laser reflection point, at or slightly above the critical density (Denavit, 1992). The forward momentum gained from the ponderomotive pressure can be of the order of that resulting from ambipolar acceleration at the back surface, with protons from the front mixing with those from the back, later on during the target blow-off (Fig. 2): The energy distribution in Figure 2b shows that some of the protons emitted forward through the rear side of the target can actually originate from the front side, but their maximum energy is definitely smaller than that of protons accelerated from the rear of the target. For protons accelerated by the ponderomotive effect at the front surface, an estimate of the velocity is given by (Wilks et al., 1992)

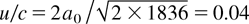
, (where

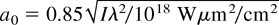
is the normalized laser field amplitude), if we assume that they are accelerated at the peak of the pulse in a region close to the critical density. This corresponds to an energy slightly less than 1 MeV, in agreement with the distribution of Figure 2b, and much smaller than the energy of protons accelerated from the rear side of the target. For all the thin target cases that we simulated (higher density target and/or higher intensity pulse), the protons accelerated at the front surface emerged at the back of the target with less energy that protons directly accelerated at the back. This second scenario, with protons from the front side accelerated through the target, will only happen if the protons at the front are around the critical surface when the main pulse hits the target. For a thin hydrogenated layer deposited on a metallic target, this is very unlikely considering the practical levels of ASE. On the other hand, this will always occur if the bulk of the target contains hydrogen.

Density profile (a) and proton distribution functions (b) at 5.3 ps, for the same parameters as Figure 1, except that the target has no density gradient at the front.

Based upon the results presented above, we conclude that the most energetic protons emitted in the forward direction that are observed in the experiments with metallic targets cannot come from the front side of the target, but are dragged from the rear surface by electrostatic fields.

2.2. Scaling of proton energies with laser irradiance

In the remainder of this article, we will therefore focus on a model aluminum target with a proton layer at the back. The prepulse effect is taken into account by starting the simulations with an exponential density ramp on the front side of the target, with a 4.1λ scale length, followed by a 2λ plateau at 2.5 nc. A 0.16λ-thick proton layer is located at the end of this plateau. The electron and ion distributions are initialized with a temperature of 1 keV. The spatial cell size and time step used in the calculation are, respectively, λ/63 and τ/126, with λ being the laser wavelength (1 μm here) and τ the laser period. The plasma is sampled with 60 particles per cell for the electrons and Al ions, and 800 particles per cell for the thin proton layer.

Figure 3 displays, at four different times, the proton distribution when this target is illuminated by a 530-fs, 1-μm-wavelength laser pulse with a maximum intensity of 1.4 × 1018 W/cm2. This distribution has a sharp cutoff that grows in time to around 16 MeV at the end of the simulation. The slope of the distribution quickly reaches the almost steady value of 2.5 MeV. We have used three particular measures to characterize the proton distribution. The first one is the maximum, or cutoff, energy, Emax, observed on the distribution. The second one is the average proton energy, Eavg, and the last one, E95, is the energy below which we can find 95% of the protons that were initially in the thin layer at the back of the target. The time evolution of these three characteristic energies is shown in Figure 4 for the same interaction parameters as in Figure 3. Each energy quickly grows up before it saturates. We can notice that this saturation is faster for Eavg and E95 than for Emax. For each of the first two curves, a final value can easily be measured: For the case illustrated in Figure 4, the final average proton energy is 2.6 MeV. These curves underline that even for very short pulses, the process of proton acceleration is a much slower one, as it takes place on an ion time scale. A typical acceleration time deduced from Figure 4 is 3 ps for the bulk of the distribution. This puts strong constraints on the simulation of this phenomenon, which must be followed for a time much larger than the laser pulse duration, and for distances of hundreds of micrometers, even for initially micrometer-thin targets (see, e.g., Fig. 1c).

Proton distribution at four instants from the back of a thin aluminum plasma irradiated at 1.4 × 1018 W/cm2 by a 1-μm wavelength pulse.

Time evolution of the maximum (Emax) and average (Eavg) proton energies, as well as the energy below which 95% of the accelerated protons can be found (E95), for a thin hydrogen layer behind an aluminum foil irradiated at 1.4 × 1018 W/cm2 by a 1-μm wavelength pulse.

Figures 1c and 2a show that the proton density is almost exponential during blow-off, as a simple isothermal model suggests (Wilks et al., 2001). We have measured the gradient length of this exponential density profile at different times for a hydrogen layer accelerated at the back of an Al target irradiated at 1.4 and 8 × 1018 W/cm2. These values are summed up in Figure 5, and fit remarkably well to a simple L = vt law, with v = 0.026c and v = 0.041c, respectively, for these two irradiances. If we equate these values to the sound velocity in the proton plasma, we find electron temperatures of 630 keV and 1.6 MeV, respectively. The relevance of the isothermal model here is surprising: The hot electron temperatures just after the laser has been absorbed, for the two irradiances, are 515 keV and 1 MeV, respectively, which is not too different from those deduced above. But as the protons are accelerated, the electrons get colder: The average electron energy drops by more than a factor of four between 1.1 and 3.2 ps in our simulations! At 3.2 ps, the hot electron tails have temperatures of 200 and 480 keV only. Nevertheless, this temporal variation is not reflected in Figure 5, which shows a very linear variation of the gradient length with time.

Time evolution of the proton layer density gradient after irradiation by a 1.4 × 1018-W/cm2 (squares) or a 8 × 1018-W/cm2 (circles) pulse.

The work presented above for 1.4 × 1018 W/cm2 has been repeated for different laser intensities, so that we can study how the final proton energies scale with laser intensity. The curves plotted in Figure 6 are almost straight lines, meaning that for these parameters, the typical proton energies (Eavg and E95) are almost directly proportional to the laser irradiance. Over this range of irradiances, the fraction of laser energy absorbed by the target is almost constant, between 15% and 19%, so that the variations in proton energy reflect the fact that electrons are heated to higher temperatures at higher irradiance, accelerating the protons to higher energies. Knowing the variations of Eavg, we can compute the fraction of incident laser energy that gets coupled into proton energy: This value is consistently between 4% and 5% for the parameters of our simulations. This percentage is close to the value measured in some experiments (6% in Hatchett et al., 2000), but this agreement should not be taken too literally. The parameters of our simulations have not been chosen to match those of the experiments, and transverse effects are missing in our model. Besides, the overall proton absorption is very sensitive to the thickness of the hydrogen layer deposited at the back of the target. For a thinner layer, protons would be accelerated to a higher average energy, but they would amount to a smaller fraction of the incident pulse energy. Still, we can note that a submicrometer layer of protons at a slightly overcritical density is enough to collect 25% of the absorbed laser energy (the remaining 75% go to Al ions and, to a much smaller extent, electrons).

Final proton energies E95 and Eavg as a function of laser irradiance.

2.3. Scaling of proton energies with target parameters

The first target parameter whose influence is studied here is the foil thickness. In the simulations presented in this section, the initial plasma density profile is composed of the same exponential ramp, but the plateau length is different: It varies from 0.5 μm to 10 μm. The hydrogen layer at the rear surface of the target now always has the same thickness of 0.03λ. When the target with a 0.5-μm-thick aluminum plateau is irradiated with a 0.8 × 1018 W/cm2 laser pulse, the most energetic protons reach an energy of Emax = 10.1 MeV. Ninety-five percent of the protons are below E95 = 6 MeV, and the average proton energy is Eavg = 2.7 MeV. These figures change by less than 5% when the target thickness is varied from 0.5 μm to 4 μm and 10 μm. Specifically, the average energy is modified by less than 100 keV, which is comparable to the energy fluctuations observed when we change the simulation parameters (e.g., number of particles per cell). The same conclusion holds at larger irradiance: At 3.7 × 1018 W/cm2, for a 1-μm plateau, the maximum and average proton energies are 22.9 and 8.1 MeV, respectively, whereas a 10-μm plateau target yields 24.5 and 7.4 MeV. These simulations show that, in 1D, the target thickness does not really influence the proton energy: The changes in Eavg, Emax, and E95 are small and irregular when the target width varies between 0.5 and 10 μm. This is probably an artefact of our 1D model: Once an electron is accelerated at the front surface, its energy will be little affected by its transport through the thin, hot, collisionless target. If the typical ion acceleration time is large compared to a hot electron transit time through the target, the hot electrons will produce the same electrostatic field pattern at the rear surface, whatever the target thickness, and accelerate protons to similar energies. Conversely, in 2D or 3D geometry, electrons that are not accelerated along the laser propagation direction will form a negative cloud at the back of the target that will be all the more diffuse, and will accelerate protons to a lower energy, that the target is thicker. As mentioned in the introduction, collisional effects are not included in our model. We believe that this assumption is valid as long as we are dealing with thin targets and relatively long pulses, so that the target electrons are efficiently heated during the laser–plasma interaction, rapidly making collisions unimportant.

An experiment performed at the Rutherford Appleton Laboratory showed that a prepulse at the back of the target prevents energetic proton emission when the main pulse strikes the front surface (Mackinnon et al., 2001). Previous simulations indicated that the proton beam characteristics depend on the density scale length at the back of the target (Wilks et al., 2001), and we ran complementary 1D simulations to assess the influence of this parameter. The initial plasma profile is now composed of the same exponential ramp, followed by a 2-μm aluminum plateau. The density profile of the hydrogen layer at the back of the target is varied with the constraint that it always represent the same areal density of protons. We use linear profiles with length and height varied inversely, from 2.5 nc to 0 nc on 0.06λ, and so on down to a ramp from 0.25 nc to 0 nc on 0.6λ. When the target is irradiated by a 1.4 × 1018-W/cm2 pulse at 1-μm wavelength, the final average proton energy is consistently around 4 MeV. Again, the variations of this final energy with the thickness of the proton layer is of the order of 5%, and similar fluctuations are measured on the cutoff and 95% energies around the values Emax = 13.8 MeV and E95 = 8.3 MeV.

Much of the phenomenon of proton acceleration can already be captured by studying the simplified setup of a hot plasma expansion into vacuum (Denavit, 1979; Wilks et al., 2001). In this case, we set aside the consistent description of electron heating, and start the simulations with a plasma that has already been heated to a large temperature. To further elucidate the role of the rear side density profile, and following Wilks et al. (2001), we now model the expansion of a 10-nc, 500-keV electron and cold proton plasma, in contact with the left edge of the simulation window. Three target profiles are considered: a constant density on 9 μm and a linear fall on 0.05 μm in the first case, constant density on 8.5 μm and linear fall on 1 μm, and finally a constant density on 2 μm and a linear ramp down to vacuum on 14 μm. All three profiles correspond to the same areal density and hence to the same initial total electron energy. In his article, Wilks finds that at 1600 ω0−1, the maximum proton energy is 6.5 MeV in the first case and 1.1 MeV in the third one. We have run our simulations with a λ/40 mesh size, 150 particles per mesh, and more than 160 μm of vacuum on the right of the plasma to allow free expansion over long times. We monitored the total energy of the system during the simulation to make sure it was conserved. Figure 7 plots the evolution of electron and ion kinetic energies for the first and last cases (0.05- and 14-μm density ramps). We observe how the electron kinetic energy is transferred to ions in a typical time of a few thousands of ω0−1, that is, a few picoseconds for 1-μm light. This equilibration is somewhat faster than that observed in Wilks et al. (2001): The electrons have lost more than 50% of their energy at 1600 ω0−1, whereas they had only lost 20% in Wilks et al. (2001). Results for the 1-μm ramp case have not been plotted in Figure 7, as they would superimpose almost exactly to the 0.05-μm curves. Energy exchange is only slightly slower in the long gradient case. Note that at the end of the simulation, the fastest protons reach the right edge of the simulation box, more than 160 μm away from their starting point. This is consistent with a velocity of 0.17c, and with an energy of more than 13 MeV. The cutoff proton energy is plotted in Figure 7 with open symbols, and shows that protons are actually accelerated to almost 20 MeV in the sharp gradient case, and to 15 MeV for the smoother profile. The same simulation was also run for a gradient length of 56 μm and confirms these findings: The equilibration time is somewhat longer in this case, but the final proton cutoff energy is hardly modified compared to the 14-μm case. Hence we can conclude that differences in proton acceleration and maximum energies between a sharp density profile and a smooth one, although they are still significant, are not as dramatic as the sixfold difference previously reported (Wilks et al., 2001). This lends credence to the observation made above, namely, that a variation in the density profile of the proton layer at the back of a laser-irradiated target has little influence on the maximum proton energy. There is no contradiction with the results presented in Mackinnon et al. (2001), where it was found that energetic protons were suppressed when a 100-μm scale-length plasma was created on the back surface: In addition to the slightly lower acceleration that such a large gradient will produce, the displacement of protons hundreds of micrometers away from the rear surface into the expanding plasma probably requires transverse effects to be included in the model.

Electron (dashed curves) and proton (solid curves) kinetic energies as a function of time for two plasmas expanding into vacuum (left axis). The electron temperature is 500 keV initially, and the protons are cold. Two density profiles are simulated: from 10 nc to vacuum over 0.05 μm or 14 μm. Open symbols show the maximum proton energy as a function of time for both cases (right axis).

3. TWO-DIMENSIONAL SIMULATIONS

Maksimchuk et al. (2000) have observed protons up to 1.5 MeV emitted along the laser axis from aluminum targets irradiated with 0.53-μm light. The maximum proton energy is a slowly growing function of the laser irradiance, with 1 MeV at an intensity of 1018 W/cm2 and 1.5 MeV at 3 × 1018 W/cm2. The influence of a variable intensity 2ω prepulse has also been explored in their experiments, for a main pulse of 1018 W/cm2. At 1014 W/cm2, the same results are recovered as without any prepulse. At 1015 W/cm2, the maximum proton energy peaks at 1.5 MeV and then decreases for higher prepulse intensities. The authors estimate that at this prepulse intensity, the density scale length in front of the target is a few laser wavelength.

In the 2D PIC simulations that we have run to account for these observations, the target is modeled by a 2λ homogeneous Al plasma at 5 nc, preceded by an exponential density ramp from 0.05 to 5 nc with a variable scale length. As discussed previously, the experimental target density is definitely much more than 5 nc, but we do not expect a strong dependence of our observations on this parameter, because the target width is much smaller than the electron range or radiation length for the energies of interest. At the back of the target, we use a second ion species to simulate a 0.03λ-thick, 5-nc layer of protons. We use 52 points per laser wavelength and a time step of τ/76. The Al ions and electrons are sampled with 20 particles per cell, and the proton layer with 200 particles per cell. The laser pulse is incident on target at normal incidence, and the transverse direction is that of the electric field vector (p-polarization).

For the “no prepulse” cases, we used a 1λ density scale length for the exponential ramp, and two laser irradiances of a0 = 0.45 and 0.78, corresponding respectively to 1 and 3 × 1018 W/cm2, for 0.53-μm light. The laser pulse has a cosine-squared temporal shape with a 280-fs full duration and is focused down to a 5λ full-width-at-half-maximum (FWHM) spot. The target is placed in a large box—more than 25λ large and 130λ long—and we run the simulation for about 1 ps to allow for full ion acceleration. In both cases, the laser absorption is relatively low (less than 10%). The protons at the back of the target are dragged to the right in a quasi 1D expansion. The energy cutoff is 0.75 MeV at 1018 W/cm2 and 1.5 MeV at 3 × 1018 W/cm2, in relatively good agreement with the experiment. But ion collimation is much narrower that what was measured experimentally, with less than 10° FWHM for protons above 0.5 MeV.

At 1018 W/cm2, a slight prepulse on the target front side was found experimentally to enhance the maximum ion energy to 1.5 MeV. We have run another simulation at this laser irradiance with a 3λ scale length density profile in front of the target. The laser absorption is then doubled to nearly 20% and the protons are accelerated to a higher energy of almost 1 MeV (Fig. 8). Hence, the influence of a longer density gradient in the simulations is similar to the experimental observation, but with a more modest energy increase (250 keV instead of 500 keV). Besides the twofold increase in the laser absorption, the smoother density gradient has another drastic effect on electron acceleration. Indeed, the hot electron distribution cutoff grows from less than 0.6 MeV for the 1λ case to more than 1.5 MeV for the 3λ case. On the electron distributions of Figure 9, taken at 0.35 ps, when the electrons have already slightly cooled down and accelerated the ions, we measure hot electron temperatures of 30 and 60 keV, respectively, for the λ and 3λ cases. When a long exponential profile is used (L/λ = 10), the laser absorption is dramatically increased to 50%, and the hot electron distribution develops a non-Maxwellian shape at high energy. Again, this leads to an increase in the proton cutoff energy to more than 1.2 MeV. Proton collimation is not markedly modified between the L/λ = 1 and L/λ = 10 targets.

Energetic proton distributions at 0.93 ps, for plasmas with different front-side scale length, and irradiated by a 0.53-μm laser pulse at 1018 W/cm2.

Electron distributions at the end of the laser pulse (0.35 ps), for plasmas with different front-side scale length, and irradiated by a 0.53-μm laser pulse at 1018 W/cm2.

One-dimensional simulations were run with the same plasma and laser parameters. The simulations were performed in a larger box (almost 1000λ) over a longer time (more than 3 ps). For the “no prepulse” cases, the proton energy cutoff is 0.21 MeV at 1018 W/cm2 and 0.45 MeV at 3 × 1018 W/cm2. And as far as the prepulse influence is studied, at a 1018 W/cm2 irradiance, the cutoff is 0.45 MeV with a 3λ exponential ramp and 0.80 MeV with a 10λ exponential ramp. The laser absorption is 3% in the 1λ case and 35% in the 10λ case. The kinetic energies measured with 1D simulations are somewhat smaller, probably owing to the lower laser absorption that is always observed in 1D simulations, but they indicate the same trend of higher proton energy when the density gradient on the front side is longer.

The drop in proton energy experimentally observed (Maksimchuk et al., 2000) is not reproduced in these simulations, but we can reasonably conjecture that it would eventually happen if we kept increasing the gradient length. Indeed, the laser pulse can only couple a finite energy to hot electrons. As the gradient length and hence the target thickness is increased, these hot electrons will spread over a larger volume, and their lower density will produce lower accelerating electrostatic fields. Alternatively or in addition to this effect, the hot electrons produced by a high prepulse level in the experiment may disturb the rear target surface and quench the acceleration mechanism (Mackinnon et al., 2001). Despite this difference in prepulse dependence, we conclude that proton energies observed in experiments are consistent with a rear surface acceleration mechanisms modeled by 2D PIC simulations. The maximum proton energy can be modified through changes of laser prepulse or main pulse irradiance.

4. CONCLUSION

The 1D and 2D PIC simulations presented in this article outline some features of proton acceleration during the interaction of a ultrahigh-intensity laser pulse with overdense, hydrogen-coated, metallic foils. Data presented in this article support the model of proton emission from the rear surface, driven by the hot electron ambipolar field. Simulations with proton layers on each side of the target showed that forward proton acceleration from the front side results in lower energies than directly from the rear side, for thin, metal targets. For intensities of a few 1018 W/cm2 and a given target density profile, we found that the average and maximum proton energies are almost proportional to the incident laser energy, with an energy efficiency of a few percent. This efficiency was found to depend neither on the slab thickness (as long as it is still a thin foil) nor on the density scale length of the proton layer. Finally, when the density scale length at the front of the target is increased, corresponding to a higher laser prepulse intensity, the energetic proton efficiency is also increased. Two-dimensional simulations of Maksimchuk et al.'s (2000) experiment gave cutoff energies in good agreement with their results.

ACKNOWLEDGMENTS

E. Lefebvre acknowledges useful discussions on this topic with E. d'Humières (CEA), V. Malka, and S. Fritzler (Laboratoire d'Optique Appliquée).

References

REFERENCES

Clark, E.L., Krushelnick, K., Davies, J.R., Zepf, M., Tatarakis, M., Beg, F.N., Machacek, A., Norreys, P.A., Santala, M.I.K., Watts, I. & Dangor, A.E. (2000a). Measurements of energetic proton transport through magnetized plasma from intense laser interactions with solids. Phys. Rev. Lett. 84, 670–673.Google Scholar
Clark, E.L., Krushelnick, K., Zepf, M., Beg, F.N., Tatarakis, M., Machacek, A., Santala, M.I.K., Watts, I., Norreys, P.A. & Dangor, A.E. (2000b). Energetic heavy-ion and proton generation from ultraintense laser-plasma interactions with solids. Phys. Rev. Lett. 85, 1654–1657.Google Scholar
Denavit, J. (1979). Collisionless plasma expansion into a vacuum. Phys. Fluids 22, 1384–1392.Google Scholar
Denavit, J. (1992). Absorption of high-intensity subpicosecond lasers on solid density targets. Phys. Rev. Lett. 69, 3052–3055.Google Scholar
Disdier, L., Garçonnet, J.-P., Malka, G. & Miquel, J.-L. (1999). Fast neutron emission from a high-energy ion beam produced by a high-intensity subpicosecond laser pulse. Phys. Rev. Lett. 82, 1454–1457.Google Scholar
Fews, A.P., Norreys, P.A., Beg, F.N., Bell, A.R., Dangor, A.E., Danson, C.N., Lee, P. & Rose, S.J. (1994). Plasma ion emission from high intensity picosecond laser pulse interactions with solid targets. Phys. Rev. Lett. 73, 1801–1804.Google Scholar
Gitomer, S.J., Jones, R.D., Begay, F., Ehler, A.W., Kephart, J.F. & Kristal, R. (1986). Fast ions and hot electrons in the laser-plasma interaction. Phys. Fluids 29, 2679–2688.Google Scholar
Hatchett, S.P., Brown, C.G., Cowan, T.E., Henry, E.A., Johnson, J.S., Key, M.H., Koch, J.A., Langdon, A.B., Lasinski, B.F., Lee, R.W., Mackinnon, A.J., Pennington, D.M., Perry, M.D., Phillips, T.W., Roth, M., Sangster, T.C., Singh, M.S., Snavely, R.A., Stoyer, M.A., Wilks, S.C. & Yasuike, K. (2000). Electron, photon, and ion beams from the relativistic interaction of Petawatt laser pulses with solid targets. Phys. Plasmas 7, 2076–2082.Google Scholar
Hegelich, M., Karsch, S., Pretzler, G., Habs, D., Witte, K., Guenther, W., Allen, M., Blazevic, A., Fuchs, J., Gauthier, J.-C., Geissel, M., Audebert, P., Cowan, T. & Roth M. (2002). MeV ion jets from short-pulse-laser interaction with thin foils. Phys. Rev. Lett. 89, 085002.Google Scholar
Key, M.H., Cable, M.D., Cowan, T.E., Estabrook, K.G., Hammel, B.A., Hatchett, S.P., Henry, E.A., Hinkel, D.E., Kilkenny, J.D., Koch, J.A., Kruer, W.L., Langdon, A.B., Lasinski, B.F., Lee, R.W., MacGowan, B.J., Mackinnon, A., Moody, J.D., Moran, M.J., Offenberger, A.A., Pennington, D.M., Perry, M.D., Phillips, T.J., Sangster, T.C., Singh, M.S., Stoyer, M.A., Tabak, M., Tietbohl, G.L., Tsukamoto, M., Wharton, K. & Wilks, S.C. (1998). Hot electron production and heating by hot electrons in fast ignitor research. Phys. Plasmas 5, 1966–1972.Google Scholar
Mackinnon, A.J., Borghesi, M., Hatchett, S., Key, M.H., Patel, P.K., Campbell, H., Schiavi, A., Snavely, R., Wilks, S.C. & Willi, O. (2001). Effect of plasma scale length on multi-MeV proton production by intense laser pulses. Phys. Rev. Lett. 86, 1769–1772.Google Scholar
Malka, G. & Miquel, J.-L. (1996). Experimental confirmation of ponderomotive-force electrons produced by an ultrarelativistic laser pulse on a solid target. Phys. Rev. Lett. 77, 75–78.Google Scholar
Maksimchuk, A., Gu, S., Flippo, K., Umstadter, D. & Bychenkov, V.Yu. (2000). Forward ion acceleration in thin films driven by a high-intensity laser. Phys. Rev. Lett. 84, 4108–4111.Google Scholar
Pukhov, A. (2001). Three-dimensional simulations of ion acceleration from a foil irradiated by a short-pulse laser. Phys. Rev. Lett. 86, 3562–3565.Google Scholar
Snavely, R.A., Key, M.H., Hatchett, S.P., Cowan, T.E., Roth, M., Phillips, T.W., Stoyer, M.A., Henry, E.A., Sangster, T.C., Singh, M.S., Wilks, S.C., Mackinnon, A., Offenberger, A., Pennington, D.M., Yasuike, K., Langdon, A.B., Lasinski, B.F., Johnson, J., Perry, M.D. & Campbell, E.M. (2000). Intense high-energy proton beams from Petawatt-laser irradiation of solids. Phys. Rev. Lett. 85, 2945–2948.Google Scholar
Wilks, S.C., Kruer, W.L., Tabak, M. & Langdon, A.B. (1992). Absorption of ultra-intense laser pulses. Phys. Rev. Lett. 69, 1383–1386.Google Scholar
Wilks, S.C., Langdon, A.B., Cowan, T.E., Roth, M., Singh, M, Hatchett, S., Key, M.H., Pennington, D., Mackinnon, A. & Snavely, R.A. (2001). Energetic proton generation in ultra-intense laser-solid interactions. Phys. Plasmas 8, 542–549.Google Scholar
Zhidkov, A. & Sasaki, A. (2000). Effect of field ionization on interaction of an intense subpicosecond laser pulse with foils. Phys. Plasmas 7, 1341–1344.Google Scholar
Figure 0

Initial density profile (a), electrostatic field at 1.1 ps (b), density profile (c), and proton distribution functions (d) at 5.3 ps. The target is an aluminum foil covered with two proton layers at the front (dark grey) and back (light grey), with an exponential density profile at the front. It is irradiated by a 530-fs, 2 × 1018-W/cm2 pulse at 1-μm wavelength.

Figure 1

Density profile (a) and proton distribution functions (b) at 5.3 ps, for the same parameters as Figure 1, except that the target has no density gradient at the front.

Figure 2

Proton distribution at four instants from the back of a thin aluminum plasma irradiated at 1.4 × 1018 W/cm2 by a 1-μm wavelength pulse.

Figure 3

Time evolution of the maximum (Emax) and average (Eavg) proton energies, as well as the energy below which 95% of the accelerated protons can be found (E95), for a thin hydrogen layer behind an aluminum foil irradiated at 1.4 × 1018 W/cm2 by a 1-μm wavelength pulse.

Figure 4

Time evolution of the proton layer density gradient after irradiation by a 1.4 × 1018-W/cm2 (squares) or a 8 × 1018-W/cm2 (circles) pulse.

Figure 5

Final proton energies E95 and Eavg as a function of laser irradiance.

Figure 6

Electron (dashed curves) and proton (solid curves) kinetic energies as a function of time for two plasmas expanding into vacuum (left axis). The electron temperature is 500 keV initially, and the protons are cold. Two density profiles are simulated: from 10 nc to vacuum over 0.05 μm or 14 μm. Open symbols show the maximum proton energy as a function of time for both cases (right axis).

Figure 7

Energetic proton distributions at 0.93 ps, for plasmas with different front-side scale length, and irradiated by a 0.53-μm laser pulse at 1018 W/cm2.

Figure 8

Electron distributions at the end of the laser pulse (0.35 ps), for plasmas with different front-side scale length, and irradiated by a 0.53-μm laser pulse at 1018 W/cm2.