Introduction
The development of high-intensity laser beam makes the feasibility of investigating extremely interesting non-linear phenomena like self-focusing in a relativistic regime. Relativistic self-focusing (RSF) occurs on account of high-intensity laser field resulting in quiver motion of electrons, which further modifies the plasma dielectric constant. Because of potential applications of RSF in wide applications such as plasma-based accelerators, inertial confinement fusion (ICF), high harmonic generation, laser-driven fusion, and X-ray lasers (Close et al., Reference Close, Giuliano, Hellwarth, Hess, Mcclung and Wagner1966; Sun et al., Reference Sun, Ott, Lee and Guzdar1987; Chen and Sudan, Reference Chen and Sudan1993; Esarey et al., Reference Esarey, Sprangle, Krall and Ting1996; Reference Esarey, Sprangle, Krall and Ting1997; Faure et al., Reference Faure, Malka, Marques, Amiranoff, Courtois, Najmudin, Krushelnick, Salvati, Dangor, Solodov, Mora, Adam and Heron2000; Chien et al., Reference Chien, Chang, Lee, Lin, Wang and Chen2005; Gupta et al., Reference Gupta, Hur, Hwang, Suk and Sharma2007; Yazdani et al., Reference Yazdani, Cang, Sadighi-Bonabi, Hora and Osman2008), it has become a subject of keen interest these days. Ponderomotive self-focusing (PSF) is another non-linear phenomenon, which plays significant role in describing the propagation characteristics of the laser beam. It occurs due to expulsion of electrons from the high-intensity region, thereby modifying dielectric constant due to ponderomotive force. It is established that PSF sets in simultaneously with RSF and cannot be separated as ‘relativistic + ponderomotive’ self-focusing. Theoretical and experimental investigations on self-focusing of different laser beam profiles such as Gaussian (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Esarey et al., Reference Esarey, Sprangle, Krall and Ting1997; Sharma et al., Reference Sharma, Verma and Sodha2004; Kumar et al., Reference Kumar, Gupta and Sharma2006; Sadighi-Bonabi et al., Reference Sadighi-Bonabi, Navid and Zobdeh2009b), cosh-Gaussian (ChG) (Patil et al., Reference Patil, Navare, Takale and Dongare2009; Gill et al., Reference Gill, Mahajan and Kaur2011; Aggarwal et al., Reference Aggarwal, Vij and Kant2014; Nanda and Kant, Reference Nanda and Kant2014), Hermite-cosh-Gaussian (HChG) (Belafhal and Ibnchaikh, Reference Belafhal and Ibnchaikh2000; Patil et al., Reference Patil, Takale, Navare and Dongare2010), elliptical Gaussian (Soni and Nayyar, Reference Soni and Nayyar1980; Konar and Sengupta, Reference Konar and Sengupta1994), and super Gaussian beams (Karlsson and Anderson, Reference Karlsson and Anderson1992; Gill et al., Reference Gill, Mahajan, Kaur and Gupta2012; Reference Gill, Kaur and Mahajan2015) have been reported in recent years. However, the main thrust in most of the studies is directed particularly toward analysis of propagation behavior of Gaussian laser beam.
Hermite-sinusoidal-Gaussian (HSG) beams have been introduced as an exact solution of paraxial wave equation (Casperson and Tovar, Reference Casperson and Tovar1998; Tovar and Casperson, Reference Tovar and Casperson1998). ChG beams are the special cases of HSG beams. These laser beams with decentered irradiance are attracting a wide range of attention in research due to their flat top shape with higher efficient power. They confine a high portion of their energy to the outer lobes of the beam, and their transverse intensity distribution depends sensitively on the decentered parameter. This makes the decentered parameter playing a crucial role on the self-focusing characteristics of the laser beam. ChG beams have a wide range of application in different optical systems (Lü et al., Reference Lü, Ma and Zhang1999; Lü and Luo, Reference Lü and Luo2000) and other technological issues (Chu, Reference Chu2007; Chu et al., Reference Chu, Ni and Zhou2007). They are useful in many applications where same intensity of beam for longer period is desirable (Konar et al., Reference Konar, Mishra and Jana2007). On the basis of superposition of laser beams, a group of virtual sources that generate a ChG beam has been reported (Zhang et al., Reference Zhang, Song, Chen, Ji and Shi2007). Gill et al. (Reference Gill, Mahajan and Kaur2011) studied the propagation characteristics of ChG laser beam in plasma taking into account combined effect of relativistic and ponderomotive non-linearities. They have observed that the extent of self-focusing can be enhanced by choosing a suitable decentered parameter. Moreover, 20 Rayleigh lengths are also observed in their investigation. However, their studies are limited to weakly relativistic regime, and therefore more appropriate investigation is needed. Habibi and Ghamari (Reference Habibi and Ghamari2015) in their work investigated the RSF of modified ChG laser beam through cold quantum plasma. In their work, they observed that ChG laser beam causes better self-focusing in comparison with Gaussian laser beam. A few studies had been recently reported in understanding the proper selection of decentered parameter in HChG laser beam and its role in control dynamics of self-focusing (Nanda et al., Reference Nanda, Kant and Wani2013a, Reference Nanda, Kant and Wani2013b). The result shows that decentered parameter (b) and plasma density ramp affect the nature of self-focusing and defocusing in HChG laser beam.
It is highlighted from the review of the literature that efficient interaction of high-power laser with plasma may produce highly focused beam due to a combined effect of relativistic and ponderomotive non-linearities. The focusing of laser can further be enhanced using slowly increasing plasma density ramp as introduced by Gupta et al. (Reference Gupta, Hur, Hwang, Suk and Sharma2007). Usually when high-power laser of a given spot size propagates in higher density plasma, the oscillation amplitude increases significantly due to the growth of relativistic mass effect. However, a plasma slab of slowly increasing density acts as a narrowing channel that reduces oscillation amplitude with increased frequency due to adiabatic invariance. Hence, self-focusing of the beam is enhanced as the beam propagates deeper into the plasma. The length of the ramp density for optimum focusing effect is determined by laser plasma parameters. Much larger length may cause plasma density shoot to infinity (an unphysical situation) and the theory may not be valid. The mechanisms of plasma density transition trapping have well inspired the theoretical and experimental interests. Coppi et al. (Reference Coppi, Nassi and Sugiyama1992) established that the ramping to achieve peaked density profiles is important for achieving ignition conditions in the high-field tokamak IGNITOR. The use of density ramp may also allow ignition to be achieved without the complication of rf heating and pallet injection in a transient high-field tokamak burning plasma experiment (Hu et al., Reference Hu, Horton, Zhu and Porcelli2003). In a laser wake-field acceleration (LWFA) experiment conducted by Kim et al. (Reference Kim, Kim and Yoo2011) in an upward density ramp structure using 20-TW laser system, they observed that the electron energy was higher than that from the uniform density. Sadighi-Bonabi et al. (Reference Sadighi-Bonabi, Habibi and Yazdani2009a) in their theoretical investigation reported that the choice of proper density ramp leads to a laser beam propagation deep into the plasma up to several Rayleigh lengths. Habibi and Ghamari (Reference Habibi and Ghamari2012) in their investigation on non-stationary self-focusing of high-intense laser beam observed that by using upward increasing ramp, the focusing is stronger at the rear of the pulse than on the front.
In the recent past, Patil and Takale (Reference Patil and Takale2013a) studied self-focusing of Gaussian laser beam in a weakly relativistic and ponderomotive regime using density ramp. However, the propagation characteristics of ChG laser beam in similar plasma environment are still not studied to the significant extent. Thus, the potential of using such a laser beam needs to be explored. In view of this motivation, authors have investigated the propagation of ChG laser beam in a relativistic and ponderomotive plasma with upward increasing plasma density ramp. The temporal aspects of the problem are described by different time scales. Let T 0 = 2π/ω0 be the laser period, τ0 the pulse duration, τpe the electron plasma period, and τpi the ion plasma period. Following Brandi et al. (Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993b), the inequalities playing a critical role in various non-linear mechanisms can be considered as: (i) τ0 ≫ τpe ≫ T 0, (ii) τ0 ≈ τpe ≫ T 0, (iii) τpe ≫ τ0 ≫ T 0. These inequalities define different operational time regime for the onset of various non-linear mechanisms. We consider “long pulse” time regime, which correspond to case (i). In addition, we also take τpe <T 0 < τpi (relativistic–ponderomotive), as it corresponds to immobile ions. It may further be mentioned that relativistic non-linearity is set up instantaneously, while relativistic–ponderomotive is operational in long time scale (Hora, Reference Hora1975; Brandi et al., Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993a). We have setup the wave equation by applying Wentzel–Kramers–Brillouin (WKB) and paraxial ray approximation (PRA) and solved them numerically by using Runge–Kutta fourth-order method. The decentered parameter (b) and other laser plasma parameters are optimized in such a way that the beam propagates up to several Rayleigh lengths. In “Analysis” section, the effective plasma permittivity is described in brief. In “Evolution of spot size” section, we have setup the non-linear differential equation governing the propagation of ChG beams. Results are discussed in “Numerical results and discussion” section, and the last section is devoted to conclusions drawn.
Analysis
The electric vector of the ChG laser beam propagating with an angular frequency “ω0” through non-uniform plasma along z-axis can be expressed as:
$${\bf E} = \hat xA(r,z)\exp \left[ {\iota \left( {{\rm \omega} _0 t - \int_0^z k(z){\rm d}z} \right)} \right]$$where r is the radial part in a cylindrical coordinate system. 
$k(z) = ({\rm \omega} _0 /c)\sqrt {{\rm \varepsilon} _0 (z)}, {\rm \varepsilon} _0 (z)$ is the plasma dielectric constant on the axis of the beam and c is the speed of light in vacuum. Initial distribution of the ChG laser beam A(r, 0) is given by
$$A(r,0) = A_{00} (0)\exp \left( { - \displaystyle{{r^2} \over {r_0^2}}} \right){\rm Cosh}(\Omega _0 r)$$where A 00 (0) is the amplitude at r = z = 0, Ω0 is the cosh factor, and r 0 is the initial width of the beam. For z > 0, the field distribution is given by
$$\eqalign{A(r,z) =& \displaystyle{{A_{00}} \over {2f}}\exp \left( {\displaystyle{{b^2} \over 4}} \right)\left[ {\exp \left\{ { - {\left( {\displaystyle{r \over {r_0f}} + \displaystyle{b \over 2}} \right)}^2} \right\}} \right. \cr & \left. { + \exp \left\{ { - {\left( {\displaystyle{r \over {r_0f}} - \displaystyle{b \over 2}} \right)}^2} \right\}} \right]} $$here b = Ω0 r 0 is the decentered parameter. It is worth noting here that just by taking Ω0 = 0 or equivalently b = 0, we cannot recover Gaussian distribution. In the present study, we emphasize on underdense non-uniform plasma modeled by an upward plasma density ramp profile n(ξ) = n 0 tan (ξ/d) similar to Kant and Wani (Reference Kant and Wani2015) and Aggarwal et al. (Reference Aggarwal, Kumar and Kant2016). Such type of underdense unmagnetized plasma changes with normalized propagation distance 
$\xi = z/kr_0^2 $ along the z direction. In the presence of an intense laser beam, the plasma electrons experience a relativistic–ponderomotive force, which may be represented as (Borisov et al., Reference Borisov, Borovskiy, Shiryaev, Korobkin, Prokhorov, Solem, Luk, Boyer and Rhodes1992; Brandi et al., Reference Brandi, Manus, Mainfray and Lehner1993a, Reference Brandi, Manus, Mainfray, Lehner and Bonnaudb):
$$F_{\rm p} = - m_0 c^2 \nabla ({\rm \gamma} - 1)$$The relativistic factor γ takes the form
$${\rm \gamma} = (1 + a^2 )^{1/2} $$where a = e|A|/m 0cω0. –e and m 0 are the electron charge and rest mass, respectively. In the front of laser beam, the radial component of the ponderomotive force pushes the plasma electrons radially outward. The joint impact of a relativistic–ponderomotive force and intensity dependence on electron mass causes correction in the electron density given by the relation (Tripathi et al., Reference Tripathi, Taguchi and Liu2005)
$$n_{\rm e} = n \left[ {1 + \displaystyle{{c^2} \over {{\rm \omega} _{\rm p}^2}} \nabla _ \bot ^2 ({\rm \gamma} - 1)} \right]$$We have considered the non-linear contribution due to density modification in the present model of plasma dielectric function as represented by
$${\rm \varepsilon} = 1 - \displaystyle{{{\rm \omega} _{\rm p}^2 (\xi )} \over {{\rm \omega} _0^2}} \displaystyle{{(n_{\rm e} /n)} \over {\rm \gamma}} $$where ωp(ξ) = (4πn(ξ)e 2/m)1/2 is the plasma frequency. In the paraxial region 
$r^2 \lt\!\lt r_0^2 f^2 $, plasma permittivity can be expressed by using Taylor series expansion around r = 0 as
$${\rm \varepsilon} = {\rm \varepsilon} _0 - \displaystyle{{r^2} \over {r_0^2}} \Phi $$where
$${\rm \varepsilon} _0 = 1 - \displaystyle{{{\rm \omega} _{\rm p}^2} {(\rm \xi)} \over {{\rm \omega} _0^2 {\rm \gamma} _0}} \left[ {1 - \displaystyle{{c^2} \over {{\rm \omega} _{\rm p}^2}} \displaystyle{{a_0^2 (2 - b^2 )} \over {{\rm \gamma} _0 r_0^2 f^4}}} \right]$$and
$$\eqalign{\Phi =& \displaystyle{{{\rm \omega }_{\rm p}^2} {(\rm \xi)} \over {4{\rm \omega }_0^2 }}\displaystyle{{a_0^2 (2 - b^2)} \over {{\rm \gamma }_0^3 f^4}} \left[ {1 + \displaystyle{{c^2} \over {3{\rm \omega }_{\rm p}^2 {\rm \gamma }_0r_0^2 f^2(2 - b^2)}}} \right. \cr & \left. \vphantom{1 + \displaystyle{{c^2} \over {3{\rm \omega }_{\rm p}^2 {\rm \gamma }_0r_0^2 f^2(2 - b^2)}}} {\left\{ {(12 - 12b^2 - b^4)\displaystyle{{a_0^2 } \over {\,f^2}} + 16(6 - 6b^2 + b^4)} \right\}} \right]} $$here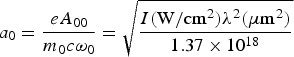 
$a_0 = \displaystyle{{eA_{00}} \over {m_0 c{\rm \omega} _0}} = \sqrt {\displaystyle{{I({\rm W}/{\rm cm}^2 ){\rm \lambda} ^2 ({\rm \mu m}^2 )} \over {1.37 \times 10^{18}}}} $ and 
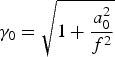$\gamma _0 = \sqrt {1 + \displaystyle{{a_0^2} \over {f^2}}} $.
Evolution of spot size
The non-linear propagation of laser beam in non-uniform plasma be governed by the generalized wave equation given by
$$\displaystyle{{\partial ^2 {\bf E}} \over {\partial z^2}} + \nabla _ \bot ^2 {\bf E} + \displaystyle{{{\rm \omega} _o^2} \over {c^2}} \quad {\rm \epsilon} {\bf E} = 0$$The amplitude E of electric field given by Eq. (1) satisfies Eq. (11). Hence substituting, for E and using WKB approximation, we neglect 
$\partial ^2 {\bf A}/\partial z^2 $. The resulting wave equation reduces to
$$ -\!2\iota k\displaystyle{{\partial A} \over {\partial z}} + \nabla _ \bot ^2 A - \displaystyle{{r^2} \over {r_0^2}} \displaystyle{{{\rm \omega} _0^2} \over {c^2}} \Phi A = 0,$$Introducing eikonal 
$A = A_0 \exp [ - \iota k(z)S]$, where A 0 and S are the real functions of space variables r and z. Substituting for A in above equation and separating real and imaginary parts, we get
$$2\displaystyle{{\partial S} \over {\partial z}} + \left( {\displaystyle{{\partial S} \over {\partial r}}} \right)^2 - \displaystyle{1 \over {k^2 A_0}} \left( {\displaystyle{{\partial ^2 A_0} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial A_0} \over {\partial r}}} \right) + \displaystyle{{2S} \over k}\displaystyle{{\partial k} \over {\partial z}} + \displaystyle{{r^2} \over {r_0^2}} \displaystyle{\Phi \over {{\rm \epsilon} _0}} = 0$$and
$$\displaystyle{{\partial A_0^2} \over {\partial z}} + A_0^2 \left( {\displaystyle{{\partial ^2 S} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial S} \over {\partial r}}} \right) + \displaystyle{{\partial A_0^2} \over {\partial r}}\displaystyle{{\partial S} \over {\partial r}} + \displaystyle{{A_0^2} \over k}\displaystyle{{\partial k} \over {\partial z}} = 0$$Following Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) and Sodha et al. (Reference Sodha, Ghatak and Tripathi1976), we expand the eikonal S in PRA as
$$S = \displaystyle{{r^2} \over 2}{\rm \beta} _0 (z) + \phi _0 (z)$$where the parameter β0 (z) = (1/f)(df/dz) may be interpreted as the curvature of the main beam, ϕ 0 (z) is a constant whose value is not required for further analysis. Substituting for 
$A_0^2 ( = A^2 )$ and S from Eq. (3) and Eq. (15), respectively, into Eq. (13) and equating coefficients of r 2 on both sides, we obtain the equation governing dimensionless beam width parameter f in the form
$$\eqalign{&\displaystyle{{d^2f} \over {d\xi ^2}} = \displaystyle{{12 - 12b^2 - b^4} \over {3f^3}} - \displaystyle{1 \over {2\varepsilon _0}}\displaystyle{{d{\rm \varepsilon }_0} \over {d\xi }}\displaystyle{{df} \over {d\xi }} \cr & \quad \quad \quad - \left( {\displaystyle{{{\rm \omega }_{{\rm p0}}r_0} \over c}} \right)^2\;\displaystyle{{a_0^2 (2 - b^2)\tan [\xi /d]} \over {4{\rm \gamma }_0^3 f^3}} \quad \quad \quad \cr &\qquad\quad \bigg [{1 + \displaystyle{{c^2} \over {3{\rm \omega }_{{\rm p0}}^{\rm 2} {\rm \gamma }_0r_0^2 f^2(2 - b^2)\tan [\xi /d]}}} \cr & \qquad\quad \left. {\left\{ {(12 - 12b^2 - b^4)\displaystyle{{a_0^2 } \over {\,f^2}} + 16(6 - 6b^2 + b^4)} \right\}} \right]}$$where ωp0 = (4πn 0e 2/m)1/2. Eq. (16) is a second-order non-linear differential equation, which can be solved numerically for f as a function of ξ using fourth-order Runge–Kutta method. The focusing/de-focusing of ChG laser beam depend upon the relative magnitude of various terms on the right-hand side (RHS) of Eq. (16).
Numerical results and discussion
To determine the characteristics of beam propagation in plasma with a density ramp profile, we solve the equation Eq. (16) with initial boundary conditions as f(0) = 1, f ′(0) = 0 and following a set of laser and plasma parameters; ω0 = 5 × 1014 rad/s, I = 1 × 1018 Wcm−2, and 
${\rm \lambda} = 1.06{\kern 1pt} \,{\rm \mu m}$ (N d:YAG laser). The numerical results are presented in the form of graphs as shown in Figures 1–5. With a given set of parameters, beam propagation can be achieved upto 50 Rayleigh lengths. However, for the analysis of self-focusing, we have shown propagation up to 15 Rayleigh lengths in the present study.
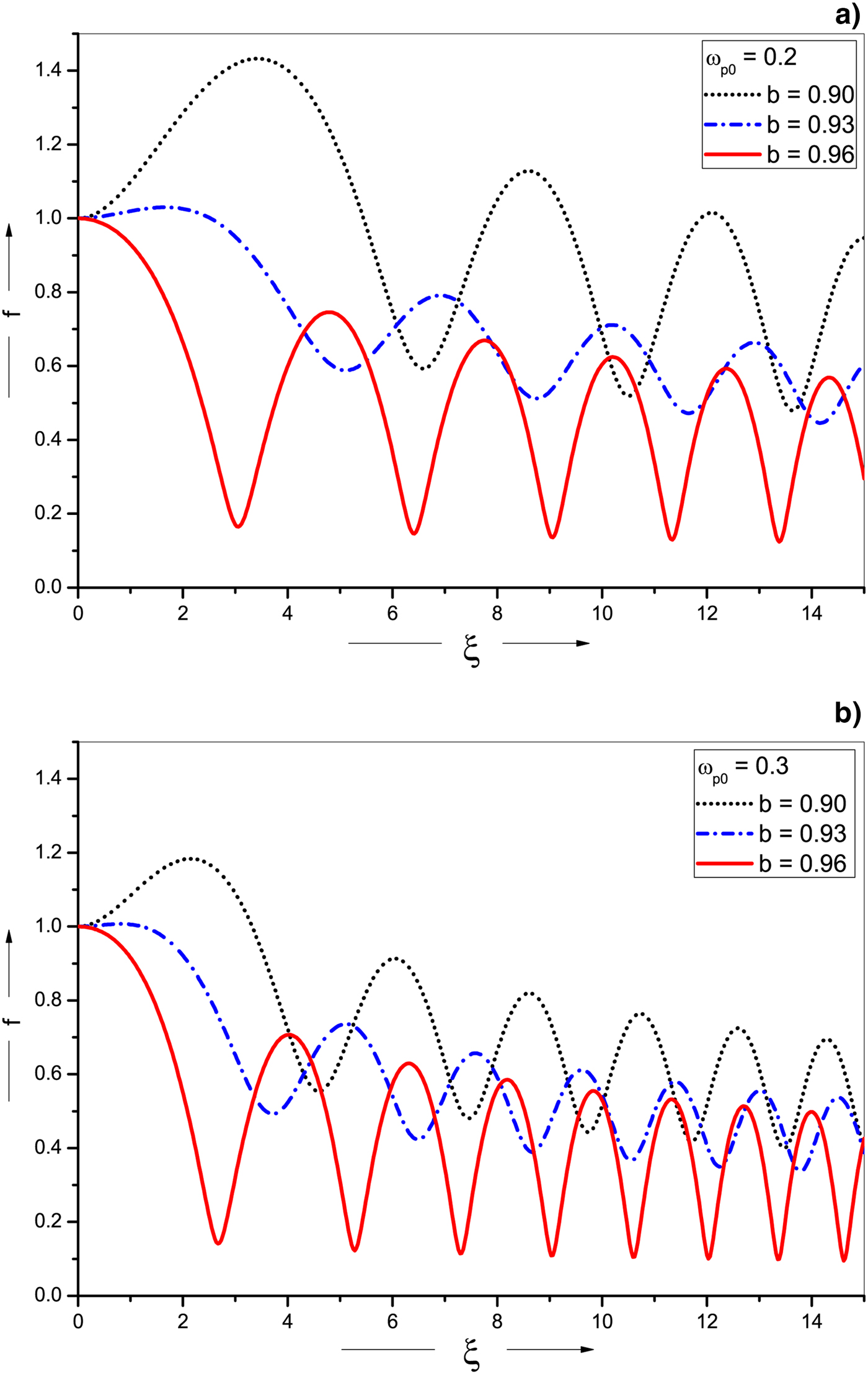
Fig. 1. Variation of beam width parameter f(ξ) with a normalized distance of propagation ξ for different values of decentered parameter b and for (a) ωp0/ω0 = 0.2 and (b) ωp0/ω0 = 0.3. The other parameters are ω0 = 5 × 1014 rad/s, r 0 = 20 μm and d = 50.
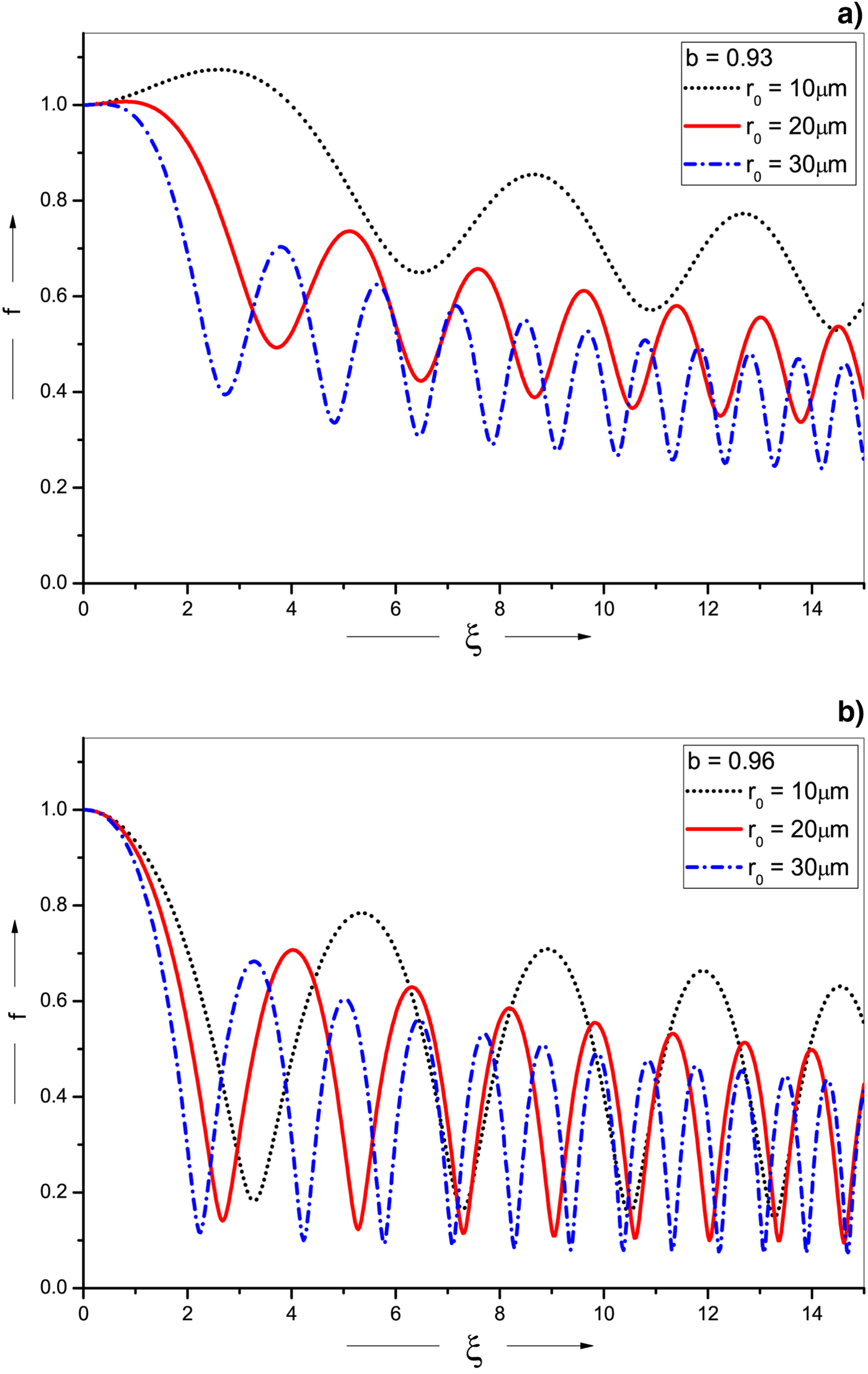
Fig. 2. Variation of beam width parameter f(ξ) with a normalized distance of propagation ξ for different values of initial width of beam r 0 and for (a) b = 0.93, ωp0/ω0 = 0.3, and (b) b = 0.96, ωp0/ω0 = 0.3. The other parameters are same as in Figure 1.
Fig. 3. Variation of beam width parameter f(ξ) with a normalized distance of propagation ξ for different values of d. The other parameters are ωp0/ω0 = 0.3, b = 0.96, r 0 = 20 μm and ω0 = 5 × 1014 rad/s.
Fig. 4. Variation of beam width parameter f(ξ) with a normalized distance of propagation ξ for Gaussian and cosh-Gaussian laser beam and for d = 50. The other parameters are same as used in Figure 3.
Fig. 5. Variation of beam width parameter f(ξ) with a normalized distance of propagation ξ for relativistic–ponderomotive and purely relativistic plasma and for d = 50. The other parameters are same as used in Figure 3.
Figure 1(a) depicts the variation of beam width parameter f with normalized distance of propagation ξ for different values of decentered parameter b (=0.90, 0.93, and 0.96) and a fixed value of relative plasma density ωp0/ω0 (=0.2). All curves in the figure exhibit oscillatory self-focusing with substantial decrease in beam width parameter and focusing length for decimal increase in the value of b. Oscillating amplitude however shows sudden decrease initially and then starts increasing with increasing value of b. This feature of sensitivity of decentered parameter b also confirms the result obtained by Nanda and Kant (Reference Nanda and Kant2014) and Gill et al. (Reference Gill, Mahajan and Kaur2011). The impact of increase in relative plasma density is clearly demonstrated in Figure 1(b), where relative plasma density ωp0/ω0 is fixed at 0.3. It is observed that there is a significant enhancement in self-focusing particularly for lower values of b. The results justify the dependency of beam width parameter f on relative plasma density (ωp0/ω0) and are in good agreement with Patil and Takale (Reference Patil and Takale2013a) and Habibi and Ghamari (Reference Habibi and Ghamari2015). Physically, this is due to the fact that at relativistic intensity, the number of relativistic electrons traveling with laser beam varies directly with plasma density. Therefore, high plasma density leads to higher current flow, which further generates a very high quasi-stationary magnetic field and hence adds to the pinching effect.
Figure 2(a) presents the variation of beam width parameter f with normalized distance of propagation ξ for b = 0.93, ωp0/ω0 = 0.3 and different value of initial beam radius r 0. It is clear from the plot that laser focusing can be enhanced by increasing initial waist size r 0 of the ChG laser beam. For r 0 = 10 μm, the laser defocuses initially and then shows oscillatory behavior with decreasing value of beam width parameter due to the presence of plasma density ramp. Increase in initial waist radius however avoids the initial defocusing of the beam. Beam width parameter and focusing length also reduce rapidly for higher values of r 0. Self-focusing is more pronounced for b = 0.96 as evident from Figure 2(b). This is due to the non-linear response of the plasma medium determined by last term on the RHS of Eq. (16). Due to direct variation of non-linear term on RHS with r 0, the increase in magnitude of r 0 values raises the dominance of this term over the first term, which is responsible for diffractional divergence. This results in an enhanced focusing effect. The results observed are better than achieved by Patil et al. (Reference Patil, Navare, Takale and Dongare2009) and Gill et al. (Reference Gill, Mahajan and Kaur2011).
The role of plasma density ramp is to avoid laser defocusing and to help in achieving better focusing. By using density ramp of suitable length, self-channeling of ChG laser is achieved without breaking up due to filamentation. However, much larger length of density ramp causes laser to reflect due to overdense plasma effect (Gupta et al., Reference Gupta, Hur, Hwang, Suk and Sharma2007). The extent of focusing and focusing length can be controlled with the slope of ramp density determined by d parameter. It is evident from Figure 3, which represents the variation of beam width parameter f with a normalized distance of propagation ξ for different values of d. With the increase in the value of d parameter, the slope of ramp decreases monotonically causing delayed focusing and increase in the minimum of beam width parameter. For a sufficiently high value of d, the slope of ramp approaches zero and hence indicates uniform density. In this case, focusing length and extreme values of beam width parameter stabilize and do not change further.
Using optimized parameters, we plot Figure 4, showing the behavior of the beam width parameter f for both Gaussian and ChG laser beam together as a function of normalized distance of propagation ξ in the presence of plasma density ramp. It is worth mentioning here that, Eq. (16) does not reduce for exactly Gaussian beam merely by putting b = 0. In view of comparing the results with ChG laser beam, the differential equation governing the beam width parameter is separately derived for Gaussian laser beam and the results are plotted for similar set of laser and plasma parameters. It is observed from the curves that rapid and sharp self-focusing occur in case of ChG laser beam relative to Gaussian laser beam. The potential application of guiding ChG laser beam up to many Rayleigh lengths with continuously reducing beam width parameter may be useful for the scientist and researchers working on laser-induced fusion, ICF, and other plasma-based accelerators. All these applications require longer propagation of laser beam in plasma with high intensity. Hence, intense laser pulses guiding in plasma channel become more and more important.
At last, in Figure 5, we present the comparison of self-focusing action as a consequence of relativistic–ponderomotive and purely relativistic non-linearities for an optimized set of parameters. As usual oscillatory self-focusing due to relative dominance of non-linearity and diffraction effects is observed in both the cases. However, for relativistic–ponderomotive plasma, the effect of ponderomotive non-linearity assist the relativistic effect and facilitates the self-focusing. As a result, self-focusing occurs earlier and to a larger extent. The results support the earlier work by Patil and Takale (Reference Patil and Takale2013b) and Aggarwal et al. (Reference Aggarwal, Kumar and Singh Gill2017).
Conclusion
The present paper is dedicated to study the propagation of ChG laser beam through non-uniform plasma with relativistic and ponderomotive non-linearities. The analysis is carried out using most popular WKB and PRA approach and the results obtained are found to be very encouraging in comparison with Gaussian laser profile. It is observed in the present study that decentered parameter and initial beam radius alongwith other parameters play a key role in self-focusing of the ChG laser beam. Decimal change in decentered parameter has a significant effect on the propagation characteristics of the beam. Plasma density ramp leads to strong self-focusing with reduced focusing length of ChG laser beam. Proper selection of laser plasma parameters and inserting plasma density ramp of suitable length can enhance laser propagation up to several Rayleigh lengths to guide laser beam propagation deep into the plasma. Our results are thus useful for the scientist working on ICF, plasma-based accelerators, and other applications where long distance propagation of focused laser beam is required.
Acknowledgment
The authors Harish Kumar and Richa are thankful to the RIC of I.K. Gujral Punjab Technical University, Kapurthala (India) for their support. Dr. Munish Aggarwal is thankful to S. Sukhbir Singh Chattha, the Director of Academic Affairs, Dr. Y. S. Randhawa, Director Lyallpur Khalsa College of Engineering, Jalandhar, for giving good research environment.
