Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T15:57:32.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Self focusing of a laser pulse in plasma with periodic density ripple

Published online by Cambridge University Press:  19 March 2009

Sukhdeep Kaur  and
A.K. Sharma
Sukhdeep Kaur*
Affiliation:
Center for Energy Studies, Indian Institute of Technology Delhi, New Delhi, India
A.K. Sharma
Affiliation:
Center for Energy Studies, Indian Institute of Technology Delhi, New Delhi, India
*
Address correspondence and reprint requests to: S. Kaur, Center for Energy Studies, Indian Institute of Technology Delhi, New Delhi-110016, India. E-mail: sukhdeep.iitd@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Propagation of an intense laser pulse in plasma with a periodically modulated density is considered using envelope equations. The laser induces modifications of the plasma refractive index via relativistic and ponderomotive nonlinearities. In the region of high plasma density, the self focusing effect of nonlinearity suppresses the diffraction divergence, and the laser converges. As the beam enters into the low density region, the diffraction tends to diverge it offsetting the convergence due to the curvature it has acquired. For a given set of plasma parameters, there is a critical power of the laser above which it propagates in a periodically focused manner. Below this power the laser undergoes overall divergence. At substantially higher powers, the laser beam continues to converge until the saturation effect of nonlinearity suppresses the self focusing and diffraction predominates. The effect of density ripple is to cause overall increase in the self focusing length. The minimum spot size decreases with the wave number of the ripple.

Keywords

Density rippleLaser propagationSelf focusing
Type
Research Article
Information
Laser and Particle Beams , Volume 27 , Issue 2 , June 2009 , pp. 193 - 199
Copyright
Copyright © Cambridge University Press 2009

1. INTRODUCTION

Currently there is significant interest in intense short pulse laser propagation through plasmas with density ripple (Gill & Saini (Reference Gill and Saini2007). Some of those studies have been motivated by the need for resonant generation of third and higher harmonics. In a homogeneous plasma, the harmonic generation process is a non-resonant one as the nth harmonic wave number k n≠n k 1, where k 1 is the wave number of the fundamental laser. A density ripple of suitable wave number q = k n – nk 1, may turn the process into a resonant one. Hence, efforts have been made to create suitable density ripples in plasmas. This kind of density ripple may be observed in gas-jet plasma experiment. Lin et al. (Reference Lin, Chen, Pai, Kuo, Lee, Wang and Chen2006) have recently used a 10 TW, 45 fs, 810 nm, and 10 Hz Ti: sapphire laser, to accomplish this. The laser beam was split into two beams. One beam, moving along $ \hat x$, was a machining pulse for producing the periodic plasma density profile, and the other one, launched 10 ns later and propagating along $ \hat z$ was a probe pulse. The machining pulse, having periodic intensity variation in transverse direction $ \hat z$, and intensity at the maxima exceeding the threshold for optical field ionization, was projected transversely on a neutral gas jet. In positions of intensity, maxima plasma was formed. After the passage of the pulse, the interlacing layers of high density neutral gas and low density plasma were formed. When a large amplitude probe pulse propagates along $ \hat z$ through such a structure, the front of the pulse ionizes the gas, and its subsequent portion encounters plasma with longitudinal density ripple.

Kuo et al. (Reference Kuo, Pai, Lin, Lee, Lin, Wang and Chen2007) have reported fascinating results on the efficiency enhancement of relativistic third harmonic generation from an optically preformed periodic plasma wave guide. They observe five times enhancement in the yield in third harmonic generation under conditions of quasi-phase matching. Parashar and Pandey (Reference Parashar and Pandey1992) had proposed such a scheme for resonant second harmonic generation of a laser pulse in plasma. They predicted an efficiency of 10% for the second harmonic generation at 1015 W/cm2 intensity by the 1 µm laser with a density ripple of a few percent. Bulanov et al. (Reference Bulano, Esirkepov, Naumova and Sokolov2003) have studied high harmonic generation of a high intensity short laser pulse in a thin hollow channel fiber due to relativistic effects.

A primary issue in developing a theoretical understanding of harmonic generation and other nonlinear phenomena, such as parametric instabilities, in plasma with deep density ripple, is the propagation of the main laser pulse itself. In case of plasmas without density ripple, extensive studies of laser pulse propagation have been carried out. Hafizi et al. (Reference Hafizi, Ting, Sprangle and Hubbard2000) have given an elegant review of self focusing in homogeneous hot/cold plasmas. It is shown that relativistic mass effect and ponderomotive nonlinearity can lead to significant self focusing of the beam. Tripathi et al. (Reference Tripathi, Taguchi and Liu2005) have studied the ion channel formation and ion Coulomb explosion in laser produced plasmas. They have also studied the relativistic self guided propagation of fast rising flat top laser pulse with Gaussian radial intensity distribution in a plasma and subsequent electron evacuation and Coulomb explosion of ions. Much work has also been reported on self focusing and harmonic generation in thin plasma slabs (Ren et al., Reference Ren, Duda, Hemker, Mori, Katsouleas, Anstonsen and Mora2001), density ramps (Gupta et al., Reference Gupta, Hur, Hwang, Suk and Sharma2007), inhomogeneous underdense plasmas (Brandi et al., Reference Brandi, Manus and Mainfray1993; Faure et al., Reference Faure, Malka, Marques, David, Amiranoff, Phuoc and Rousse2002; Liu & Tripathi, Reference Liu and Tripathi1994), Au thin target (Torrisi et al., Reference Torrisi, Margarone, Laska, Krasa, Velyhan, Pfeifer, Ullschmied and Rycl2008), and hollow channel fiber (Chessa et al., Reference Chessa, Mora and Anstonsen Thomas1998; Feit et al., Reference Feit, Komashko, Rubenchik and Turitsyn1998). It has more applications in generation of ions, X-rays and fast multi charged ions (Laska et al., Reference Laska, Badziak, Boody, Gammino, Jungwirth, Krasa, Krousky, Parys, Pfeifer, Rohlena, Ryc, Skala, Torrisi, Ullschmied and Wolowski2007a, Reference Laska, Badziak, Gammino, Jungwirth, Kasperczuk, Krasa, Krousky, Kubes, Parys, Pfeifer, Pisarczyk, Rohlena, Rosinski, Ryc, Skala, Torrisi, Velyhan and Wolowski2007b; Faenov et al., Reference Faenov, Magunov, Pikuz, Skobelev, Gasilov, Stagira, Calegari, Nisoli, Silvestri, Poletto, Villoresi and Andreev2007), excitation of an upper hybrid wave (Purohit et al., Reference Purohit, Chauhan and Sharma2008), laser ablation (Hafeez et al., Reference Hafeez, Shaikh and Baig2008), inertial confinement fusion (Hora, Reference Hora2007), and fast ignition scheme (Ghoranneviss et al., Reference Ghoranneviss, Malekynia, Hora, Miley and He2008).

In this paper, we study the self focusing of a Gaussian laser beam in plasma with periodic density ripple, n 0 = n 00 (1 + α2 cos qz). The increase arises through relativistic mass nonlinearity and ponderomotive force induced electron density depression. In regions of high plasma density n 0, the self focusing effect dominates over the diffraction effect and the beam converges. However, as the beam enters the low density regions, the diffraction effect prevail, and the beam tend to diverge. Thus one expects a periodic self focusing of the beam. What needs to be developed is a fundamental understanding based on analytic theory and models. The present paper wants to make a contribution in this direction.

In Section 2, we study the self focusing in the limit of quadratic nonlinearity and by modeling the ripple by periodic layers (of axially uniform density) of the plasma and the free space. In this case, the equation governing the beam width parameter offers analytical solutions, giving insight into the competing processes of self focusing and diffraction. In Section 3, we study the self focusing at higher intensities, taking the axial plasma density profile to be sinusoidal. In this case, the wave equation for the beam width parameter is solved numerically for relevant parameters. In Section 4, we discuss our results.

2. SELF FOCUSING WITH QUADRATIC NONLINEARITY

Consider singly ionized plasma with periodic layers of finite and zero electron density (c.f. Fig. 1b),

(1)
\eqalign{{n_0} = & {n_0^{0}} \qquad \hbox{for } 0 \lt z \lt b_1\comma \cr {n_0} = & 0 \qquad \,\;\hbox{for } b_1 \lt z \lt b_2.}
{n_0 \lpar z+b_2 \rpar =n_0 \lpar z\rpar .}

A Gaussian laser beam is launched into the plasma with

(2)
\vec E=\hat xA\lpar r\comma \; z\rpar e^{ - i\lpar {\rm \omega} t - kz\rpar} \comma

where

(3)
\left. {A^2 } \right\vert _{z=0}=A_{00}^2 e^ {- {r^2 }/{r_0^2 }}\comma \;
k^2={{{\rm \omega} ^2 } \over {c^2 }}\comma \;

${\rm \omega} ^2\gg {\rm \omega} _p^2=4\pi n_0^0 e^2 /m$, –e and m are the electron charge and rest mass. In this limit, the wave reflections at the interfaces of layers can be neglected. Following Liu and Tripathi (Reference Liu and Tripathi1994) we may write, for z > 0

(4)
\left\vert {A^2 } \right\vert ={{A_{00}^2 } \over {\,f^2 }}e^{ - {{r^2 }/{r_0^2 f^2 }}}\comma \;

where f is the beam width parameter.

Fig. 1. Schematic of a plasma with sinusoidal density ripple (a) and rectangular density profile (b).

According to Upadhyay et al. (Reference Upadhyay, Tripath, Sharma and Pant2002), the laser imparts an oscillatory velocity to the electrons,

(5)
\vec v={{e\vec E} \over {mi{\rm \omega}{\rm \gamma} }}

where

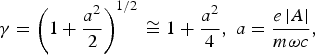
{\rm \gamma}=\left( 1+{{a^2 } \over 2}\right) ^{1/2} \, \cong 1+{{a^2 } \over 4}\comma \; a={{e\left\vert A \right\vert } \over {m{\rm \omega} c}}\comma \;

and we have assumed a 2 ≪ 1. The laser also exerts a ponderomotive force on the lectrons F p = e∇φp, where

(6)
{\rm \phi}_p=- \lpar {mc^2\! / e} \rpar \lpar {a^2 / 4}\rpar.

Under this force, the electrons move radially outward creating an ion space charge field $\vec E_s=- \nabla {\rm \phi} _s$. In the quasi-steady state, when ωpi−1 ≫ τ ≫ ωp−1 (where ωpi is the ion plasma frequency, and τ is the duration of the laser pulse), one may have φs ≅ −φp. Then the normalized electron density can be written as,

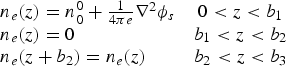
\matrix{n_e \lpar z\rpar =n_0 ^0+{1 \over {4\pi e}}\nabla ^2 {\rm \phi} _s \hfill & 0\lt z\lt b_1 \cr n_e \lpar z\rpar =0 \hfill & b_1\lt z\lt b_2 \cr n_e \lpar z+b_2 \rpar =n_e \lpar z\rpar \hfill & b_2\lt z\lt b_3}

and the effective permittivity of the plasma can be written as

(7)
{\rm \varepsilon}=1 - {{\rm \omega} _p^2 \over {\rm \omega} ^2 }{n_e / n_0^0 \over {\rm \gamma} }

It may be mentioned that for shorter pulses, the longitudinal ponderomotive force is also important. However, we do not pursue this case. In the paraxial ray approximation we expand ɛ with respect to small values of r 2,

(8)
{\rm \varepsilon}={\rm \varepsilon} _0 - \Phi {r^2 } / {r_0^2 } \comma \;

where ɛ0 ≅ 1,

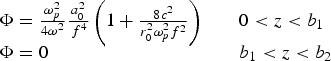
\matrix{\Phi={{{\rm \omega} _p^2 } \over {4{\rm \omega} ^2 }}{{a_0^2 } \over {\,f^4 }}\left({1+{{8c^2 } \over {r_0^2 {\rm \omega} _p^2 f^2 }}} \right)\hfill &\;\;0\lt z\lt b_1 \cr \Phi=0 \hfill & \quad b_1\lt z\lt b_2}

For 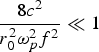${{8c^2 } \over {r_0^2 {\rm \omega} _p^2 f^2 }}\ll 1$ one may neglect the ponderomotive force induced density modification to obtain the analytical solution. This is an approximation which has limited applicability. Φ simplifies to $\Phi=\lpar {{\rm \omega} _p^2} / {4{\rm \omega} ^2} \rpar \lpar{a_0^2 } / {\,f^4 } \rpar $. Following Sodha et al. (Reference Sodha, Ghatak and Tripathi1974), equation governing the beam width parameter can be written as

(9)
\eqalignno{ {d^2 f \over d{\rm \xi} ^2 }& ={1 \over {\,f^3 }} - {{\rm \alpha} \over {\,f^3 }}\comma \; \quad \hbox{for}\quad {lb_2 } /{R_d } \lt {\rm \xi}\lt \lpar lb_2+b_1 \rpar / {R_d } \cr &= {1 \over {\,f^3 }}\comma \; \qquad \quad\; \hbox{for}\quad \lpar lb_2+b_1 \rpar / {R_d }\lt {\rm \xi}\lt \lpar \lpar l+1\rpar b_2 \rpar /R_d}

where l = 0, 1, 2, … , ${\rm \alpha}={\rm \omega}_p^2 a_0^2 r_o^2 / 4c^2 \cdot R_d = kr_0^2$ is the Rayleigh diffraction length, and ξ = z/R d0. We can solve Eq. (9) analytically by choosing proper boundary conditions. For an initially plane wave front f = 1, ${{\partial f} \over {\partial {\rm \xi} }}=0$ at ξ = 0. In the plasma region, the beam would tend to focus (${{\partial f} \over {\partial {\rm \xi} }}$ would decrease) when α > 1. In the plasma-free region ${{\partial f} \over {\partial {\rm \xi} }}$ would increase. In the region 0 < ξ< b′1, where b′1 = b/R d, multiplying Eq. (9) by $2{{\partial f} \over {\partial {\rm \xi} }}$ and integrating we get,

(10)
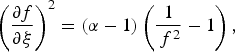
\left({{{\partial f} \over {\partial {\rm \xi} }}} \right)^2=\lpar {\rm \alpha} - 1\rpar \left({{1 \over {\,f^2 }} - 1} \right)\comma \;

Eq. (10) can be integrated to obtain,

(11)
\,f^2=1 - \lpar {\rm \alpha} - 1\rpar {\rm \xi} ^2\comma \;
(12)
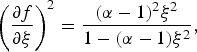
\left({{{\partial f} \over {\partial {\rm \xi} }}} \right)^2={{\lpar {\rm \alpha} - 1\rpar ^2 {\rm \xi} ^2 } \over {1 - \lpar {\rm \alpha} - 1\rpar {\rm \xi} ^2 }}\comma \;

Thus the beam self focuses (f decreases) as it propagates. At the end of the first region,

(13)
\,f_{{b}_{1}^{\prime}} = \lpar 1 - \lpar {\rm \alpha} - 1\rpar b_{1}^{{\prime} 2} \rpar ^{1/2}\comma \; b_{1}^{\prime} = b_1/R_d\comma \;
(14)
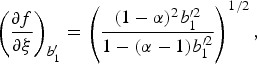
\left({\partial f \over \partial {\rm \xi} } \right)_{b_{1}^{\prime}} = \left({\lpar 1 - {\rm \alpha}\rpar ^2 {b_{1}^{\prime 2}} \over 1 - \lpar {\rm \alpha} -1\rpar {b_{1}^{\prime 2}}} \right)^{1/2}\comma \;

In the subsequent plasma free region b′1 < ξ < b′2 where b′2 = b 2/R d, we solve Eq. (9) with α = 0 following the same procedure, employing Eqs. (13) and (14) as the boundary conditions. In this region ${{\partial f} \over {\partial {\rm \xi} }}$ would increase beyond $\lpar {{\partial f} \over {\partial {\rm \xi}}}\rpar{_{b_1^{\prime}}}$, there may come a point (point of inflexion ξ = ξm) where ${{\partial f} \over {\partial {\rm \xi} }}=0$. We divide the plasma-free region into two regions: b′1 < ξ< ξm and ξm < ξ< b′2. In the former region ${{\partial f} \over {\partial {\rm \xi} }}$ is negative and Eq. (9) with α = 0 on multiplying by $2{{\partial f} \over {\partial {\rm \xi} }}$ and integrating gives,

(15)
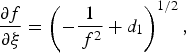
{{\partial f} \over {\partial {\rm \xi} }}=\left({ - {1 \over {\,f^2 }}+d_1 } \right)^{1/2}\comma \;
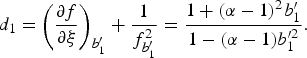
d_1=\left({\partial f \over \partial {\rm \xi} } \right)_{b^{\prime}_{1}} + {1 \over f_{b_1^{\prime}}^2} = {1+\lpar {\rm \alpha} - 1\rpar ^2 {b_1^{\prime}} \over 1 - \lpar {\rm \alpha} - 1\rpar {b_1^{\prime 2}}}.

Eq. (15) integrates to give,

(16)
\,f^2={{1+\lpar d_2 - {\rm \xi} \rpar ^2 d_1^2 } \over {d_1 }}\comma \;

where d 2 is the constant of integration. Demanding f = f b′1, at ξ = b′1 we get

(17)
d_2={{b^{\prime} _1 {\rm \alpha} } \over {1+\lpar {\rm \alpha} - 1\rpar ^2 b_1^{\prime 2} }}\comma \;
(18)
\,f^2={1 - {b_1^{\prime 2}} \lpar {\rm \alpha} - 1\rpar + {b_1^{\prime 2}} \lpar {\rm \alpha} - 1\rpar ^2 + {b_1^{\prime 4}} \lpar {\rm \alpha} - 1\rpar ^3 \over 1+\lpar {\rm \alpha} - 1\rpar ^2 {b_1^{\prime 2 }}}.

As the distance of propagation increases, then f decreases. At one point ξm, where ${\partial f \over \partial {\rm \xi} }=0\comma \; \, f_m^2={1 \over {d_1 }}$, beyond this point ${\partial f \over \partial {\rm \xi} }\gt 0$, so ξm = d 2. Beyond the ξ = ξm point, the laser starts to defocus hence ${{\partial f} \over {\partial {\rm \xi} }}$ is positive and the negative sign in Eq. (15) is replaced by a positive one. This new equation integrates to give,

(19)
\,f^2 = {1 \over d_1} \left(\left[{\sqrt {\,f_m^2 d_1 - 1} + \lpar {\rm \xi} - {\rm \xi}_m\rpar d_1} \right]^2 +1 \right)

The values of f and ${\partial f \over \partial {\rm \xi} }$ at ξ = b′2 are

(20)
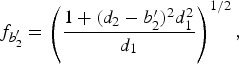
\,f_{b^{\prime} _2 }=\left({{{1+\lpar d_2 - b^{\prime} _2 \rpar ^2 d_1^2 } \over {d_1 }}} \right)^{1/2}\comma \;
(21)
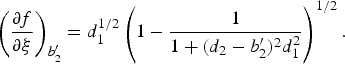
\left({{{\partial f} \over {\partial {\rm \xi} }}} \right)_{b_2^{\prime} }=d_1^{1/2} \left({1 - {1 \over {1+\lpar d_2 - b_2^{\prime} \rpar ^2 d_1^2 }}} \right)^{1/2}.

These values become the boundary conditions for solving Eq. (9) in the next plasma region, and so on. We have plotted in Figure 2a and 2b the variation of f with ξ for the following parameters:

{{{\rm \omega} _p^2 } \over {{\rm \omega} ^2 }}=0.038\comma \; {{r_0 {\rm \omega} } \over c}=75\comma \; a_0=0.1 \hbox{ and } 0.4\comma \; {{b_1 } \over {R_d }}=0.02\comma \; {{b_2 } \over {R_d }}=0.08.

For a 810 nm laser these parameters corresponds to a laser intensity I L = 2.1 × 1016 W/cm2, b 1 = 20 µm, b 2 = 60 µm. We have included in these figures the numerical results for the sinusoidal density ripple considered in the next section for competence. We choose the density modulation parameter α2 = 0.9 and n 00 is 2% of the critical density n cr. We note that for a 0 = 0.1 (Fig. 2a), the beam width parameter increases with ξ. At a 0 = 0.4 (Fig. 2b) f decreases with ξ up to a point, attains a minimum and then increases. This behavior is in contrast with a plasma without a density ripple where f, in the case of quadratic nonlinearity, monotonically decreases with ξ, attains a minimum and slightly increases. This behavior is caused by an alternate predominance of self focusing and diffraction effects. More self focusing is observed in sinusoidal density profile.

Fig. 2. (Color online) (a) The variation of beam width parameter f with ξ for rectangular and sinusoidal density profiles based on analytical and numerical models. The parameters are ωp2/ω2 = 0.038, ${{r_0 {\rm \omega} } \over c}=75$, d = 50 and a 0 = 0.1. For the sinusoidal profile modulation index α2 = 0.9 is used, and n 00 is 0.02 times the critical density. (b) The variation of beam width parameter f with ξ for rectangular and sinusoidal density profiles based on analytical and numerical models. The parameters are ωp2/ω2 = 0.038, ${{r_0 {\rm \omega} } \over c}=75$, d = 50 and a 0 = 0.4. For the sinusoidal profile modulation index α2 = 0.9 is used, and n 00 is 0.02 times the critical density.

3. SELF FOCUSING WITH ARBITRARY NONLINEARITY AND SINUSOIDAL RIPPLE

Let the equilibrium electron density n 0 be sinusoidal,

(22)
n_0=n_0^0 \lpar 1+{\rm \alpha} _2 \cos qz\rpar \comma \;

where ${\rm \alpha} _2={{n_2 } \over {n_0^0 }}$ is the depth of modulation and q is the ripple wave number. A Gaussian laser beam propagates through the plasma along $ \hat z$, with a field given by Eq. (2) and an intensity described by Eqs. (3) and (4). The electron response to the laser field is still given by Eq. (5), however, we will keep the normalized laser amplitude a as an arbitrary number. Hence the ponderomotive potential is, φp = −(mc 2/e)(γ − 1), Following Tripathi et al. (Reference Tripathi, Taguchi and Liu2005), the modified electron density can be written as,

(23)
n_e=n_0^0 \lpar 1+{\rm \alpha} _2 \cos qz\rpar +{1 \over {4\pi e}}\nabla ^2 {\rm \phi} _s\comma \;

$n_e=n_0^0 \lpar 1+{\rm \alpha} _2 \cos qz\rpar$ and one obtains in a underdense plasma ɛ0 ≅ 1,

(24)
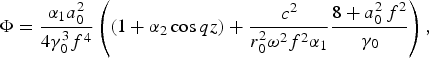
\Phi={{{\rm \alpha} _1 a_0^2 } \over {4{\rm \gamma} _0^3 f^4 }} \left({{\lpar 1+{\rm \alpha} _2 \cos qz\rpar }+{c^2 \over r_0^2 {\rm \omega} ^2 f^2 {\rm \alpha} _1 }{8 + a_0^2\, f^2 \over {\rm \gamma}_0}} \right)\comma \;

where ${\rm \alpha} _1={{{\rm \omega} _{\,p0}^2 } \over {{\rm \omega} ^2 }}$ is the ratio of plasma density to critical density.

The wave equation governing the laser field in the Wentzel-Kramers-Brillouin approximation is given by

(25)
2ik_0 {{\partial A} \over {\partial z}}+\nabla _ \bot ^2 A+{{{\rm \omega} ^2 } \over {c^2 }}\Phi=0\comma \;

Expressing A = A 0 (z, r) exp [ik 0s(z, r)], where A 0 and s are real, separating out the real and imaginary parts of the equation we obtain, two coupled equation for A 2 and s.

Expanding s in powers of r 2 as $s = s_0 + {{{\rm \beta} r^2 } \over 2}$ with ${\rm \beta}={1 \over f}{{\partial f} \over {\partial z}}$, one of these equations gives A2 given by Eq. (4). On equating the coefficients of r 2 on both sides in the other equation we obtain the equation governing the beam width parameter.

(26)
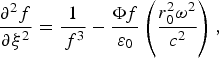
{{\partial ^2 f} \over {\partial {\rm \xi} ^2 }}={1 \over {\,f^3 }} - {{\Phi f} \over {{\rm \varepsilon} _0 }}\left({{{r_0^2 {\rm \omega} ^2 } \over {c^2 }}} \right)\comma \;

where ${\rm \xi}=z/R_{d0}\comma $$ d=qR_d$ is the normalized ripple wave number. The first term on right-hand-side is due to diffraction while the second term is due to nonlinear self focusing. For an initially plane wave front the boundary conditions at ξ = 0 are: f = 1 and ${{\partial f} \over {\partial {\rm \xi} }}=0.$

We have solved Eq. (26) numerically. Figures 3 to 6 show the variation of the beam width parameter f as a function of normalized distance of propagation for different parameters. Figure 3 shows the variation for α1 = 0.02, α2 = 0.9, normalized ripple wave number d = 50 and normalized laser amplitude a 0 = 0.18−0.19. For a 0 ≤ 0.18 the beam slowly focuses and defocuses due to predominance of diffraction effects. At a 0 = 0.1815 the self focusing effect overall neutralizes the diffraction effect and the beam propagates in a mildly periodic manner, due to self focusing in the high density region and prevalence of diffraction in the low density region. Laser power corresponding to this value of critical power for self focusing may be treated as $P_{cr}=\left({c^3 / 8} \right)\left({0.1815\, m {\rm \omega} r_0 /e} \right)^2.$

Fig. 3. (Color online) Critical power at normalized laser amplitude a 0 = 0.18 –0.19, α1 = 0.02, α2 = 0.9, d = 50.

Fig. 4. (Color online) Variation of f with ξ for normalized laser amplitude a 0 = 0.249 – 0.2515, where the critical power can be obtained at a 0 = 0.25, α1 = 0.01, α2 = 0.2 and d = 50.

Fig. 5. (Color online) Comparison of beam width parameter at normalized laser amplitude a 0 = 0.249 – 0.5 at α1 = 0.01, α2 = 0.2, d = 50.

Fig. 6. (Color online) Variation of beam width parameter f with distance of propagation ξ, for parameters α1 = 0.02, α2 = 0.9, ${{r_0 {\rm \omega} } \over c}=75$, d = 50 and d = 80, a 0 = 1.0.

Figures 4 to 5 show the behavior of self focusing for different values of a 0 = 0.249 – 0.5, while α1 = 0.01, α2 = 0.2, ${{r_0 {\rm \omega} } \over c}=75$, d = 50. At a 0 = 0.25, the self focusing effect overall neutralizes the diffraction effect and the beam propagates in periodic manner (Fig. 4), As we increase the value of normalized laser amplitude beyond the critical value, the laser undergoes self focusing in a periodic fashion. This corresponds to the critical power for self focusing at arbitrary values $P_{cr}=\left({{{c^3 } 8}} \right)\left({0.25\, m{\rm \omega} r_0 /e} \right)^2$. At a 0 = 0.5, (Fig. 5) the beam width parameter monotonically decreases up to z = 0.55R d and beyond that monotonic increase in beam width parameter occurs. There is a strong focusing and the effect of density ripple is to overall increase the self focusing length.

Figure 6 shows the variation of beam width parameter and distance of propagation for a 0 = 1.0, α1 = 0.03, ${\rm \alpha} _2=0.9\comma \; \; {{r_0 {\rm \omega} } / c}=75$, d = 59.65 experiment by Lin et al. (2006). Beam width parameter shows very different behavior at d = 59 and 65. At normalized ripple wave number d = 59, the beam width parameter decreases to minimun spot size to z  = 0.15 R d and beyond it diffraction effects predominates. On increasing the ripple wave number to d = 65, the beam width parameter self focused and shows periodic focusing.

4. DISCUSSION

The presence of a density ripple in a plasma significantly modulates the phenomenon of self focusing. Uneven focusing/defocusing of the beam in the low and high density regions cause a ripple in the beam width parameter as a function of distance of propagation. The effect is more pronounced near the focus. For qR d = 65, α1 = 0.03, α2 = 0.9, r 0ω/c = 75, a 0 = 1.0 the beam width parameter shows periodic variation of f with ξ. However, for R d = 59 this behaviour is markedly different, the beam width parameter decreases with ξ, acquires a minimum and then rises again.

The minimum beam width parameter f min decreases with increasing laser intensity (a 02). The focusing length z min = ξminR d, at which f = f min, decreases with increasing a 02.

The present model is applicable to long pulses τ ≫ ωp−1, so that the electrons have enough time to move under the ponderomotive force. However, the pulse duration may be shorter than ωpi−1 otherwise ions will also follow the electrons, which we have ignored.

ACKNOWLEDGMENT

We thank Professor V. K. Tripathi for useful discussions.

References

REFERENCES

Brandi, H.S., Manus, C. & Mainfray, G. (1993). Relativistic self-focusing of ultraintense laser pulses in inhomogeneous underdense plasma. Phys. Rev. E 47, 3780.CrossRefGoogle Scholar
Bulano, V.S.V., Esirkepov, T.Zh., Naumova, N.M. & Sokolov, I.V. (2003). High-order harmonics from an ultraintense laser pulse propagating inside a fibre. Phys. Rev. E 67, 0164051–5.Google Scholar
Chessa, P., Mora, P. & Anstonsen Thomas, M. Jr. (1998). Numerical simulation of short laser pulse relativistic self-focusing in underdense plasma. Phys. Plasmas 5, 3451–3458.CrossRefGoogle Scholar
Faenov, A.Ya., Magunov, A.I., Pikuz, T.A., Skobelev, I.Y., Gasilov, S.V., Stagira, S., Calegari, F., Nisoli, M., Silvestri, S.De., Poletto, L., Villoresi, P. & Andreev, A.A. (2007). X-ray spectroscopy observation of fast ions generation in plasma produced by short low- contrast laser pulse irradiation of solid. Laser Part. Beams 25, 267–275.CrossRefGoogle Scholar
Faure, J., Malka, V., Marques, J.R., David, P.G., Amiranoff, F., Phuoc, K.T. & Rousse, A. (2002). Effects of pulse duration on self-focusing of ultra-short lasers in underdense plasmas. Phys. Plasmas 9, 756–759.CrossRefGoogle Scholar
Feit, M.D., Komashko, A.M., Rubenchik, A.M. & Turitsyn, S.K. (1998). Electron cavitation and relativistic self-focusing in underdense plasma. Phys. Rev. E 57, 7122–7125.CrossRefGoogle Scholar
Ghoranneviss, M., Malekynia, B., Hora, H., Miley, G.H. & He, X. (2008). Inhibition factor reduces fast ignition threshold for laser fusion using nonlinear force driven block acceleration. Laser Part. Beams 26, 105–111.CrossRefGoogle Scholar
Gill, T.S. & Saini, N.S. (2007). Nonlinear interaction of a ripped laser beam with an electrostatic upper hybrid wave in collisional plasma. laser Part. Beams 25, 283–293.CrossRefGoogle Scholar
Gupta, D., Hur, M., Hwang, I., Suk, H. & Sharma, A.K. (2007). Plasma density ramp for relativistic self-focusing of an intense pulse. Opt. Soc. Ame. B 24, 1155–1159.CrossRefGoogle Scholar
Hafeez, S., Shaikh, N.M. & Baig, M.A. (2008). Spectroscopic studies of Ca plasma generated by the fundamental, second, and third harmonics of a Nd: YAG laser. Laser Part. Beams 26, 41–50.CrossRefGoogle Scholar
Hafizi, B., Ting, A., Sprangle, P. & Hubbard, R.F. (2000). Relativistic focusing and ponderomotive channeling of intense laser beams. Phys. Rev. E 62, 4120–4125.CrossRefGoogle ScholarPubMed
Hora, H. (2007). New aspects for fusion energy using inertial confinement. Laser Part. Beams 25, 37–45.CrossRefGoogle Scholar
Kuo, C.C., Pai, C.H., Lin, M.W., Lee, K.H., Lin, J.Y., Wang, J. & Chen, S.Y. (2007). Enhancement of relativistic harmonic generation by an optically-preformed periodic plasma waveguide. Phys. Rev. Lett. 98, 033901–6.CrossRefGoogle ScholarPubMed
Laska, L., Badziak, J., Boody, F.P., Gammino, S., Jungwirth, K., Krasa, J., Krousky, E., Parys, P., Pfeifer, M., Rohlena, K., Ryc, L., Skala, J., Torrisi, L., Ullschmied, J. & Wolowski, J. (2007 a). Factors influencing parameters of laser ion Sources. Laser Part. Beams 25, 199–205.CrossRefGoogle Scholar
Laska, L., Badziak, J., Gammino, S., Jungwirth, K., Kasperczuk, A., Krasa, J., Krousky, E., Kubes, P., Parys, P., Pfeifer, M., Pisarczyk, T., Rohlena, K., Rosinski, M., Ryc, L., Skala, J., Torrisi, U.J., Velyhan, A. & Wolowski, J. (2007 b). The influence of an intense laser beam interaction with preformed plasma on the characteristics of emitted ion strems. Laser Part. Beams 25, 549–556.CrossRefGoogle Scholar
Lin, M.W., Chen, Y.M., Pai, C.H., Kuo, C.C., Lee, K.H., Wang, J. & Chen, S.Y. (2006). Programmable fabrication of spatial structures in a gas jet by laser machining with a spatial light modulator. Phys. Plasmas 13, 1107011–4.CrossRefGoogle Scholar
Liu, C.S. & Tripathi, V.K. (1994). Interaction of Electromagnetic Waves and Electron Beams with Plasmas. Singapore: World Scientific.CrossRefGoogle Scholar
Parashar, J. & Pandey, H.D. (1992). Second-harmonic generation of laser radiation in a plasma with a density ripple. IEEE Trans. Plasma Sci. 20, 996–999.CrossRefGoogle Scholar
Purohit, G., Chauhan, P.K. & Sharma, R.P. (2008). Excitation of an upper hybrid wave by a high power laser beam in plasma. Laser Part. Beams 26, 61–67.CrossRefGoogle Scholar
Ren, C., Duda, R.G., Hemker, R.G., Mori, W.B., Katsouleas, T., Anstonsen, T.M. Jr. & Mora, P. (2001). Compressing and focusing a short laser pulse by a thin plasma lens. Phys. Rev. E 63, 026411.CrossRefGoogle Scholar
Sodha, M.S., Ghatak, A.K. & Tripathi, V.K. (1974). Self- focusing of Laser Beams in Dielectric, Plasmas and Semiconductors. New Delhi: Tata McGraw-Hill.Google Scholar
Torrisi, L., Margarone, D., Laska, L., Krasa, A., Velyhan, A., Pfeifer, M., Ullschmied, J. & Rycl, L. (2008). Self- focusing effect in Au-target induced by high power pulsed laser at PALS. Laser Part. Beams 26, 379–387.CrossRefGoogle Scholar
Tripathi, V.K., Taguchi, T. & Liu, C.S. (2005). Plasma channel charging by an intense short pulse laser and ion coulomb explosion. Phys. Plasmas 12, 043106.CrossRefGoogle Scholar
Upadhyay, A., Tripath, I.V.K., Sharma, A.K. & Pant, H.C. (2002). Asymmetric self focusing of a laser pulse in plasma. J. Plasma Phys. 68, 75–80.CrossRefGoogle Scholar
Figure 0

Fig. 1. Schematic of a plasma with sinusoidal density ripple (a) and rectangular density profile (b).

Figure 1

Fig. 2. (Color online) (a) The variation of beam width parameter f with ξ for rectangular and sinusoidal density profiles based on analytical and numerical models. The parameters are ωp2/ω2 = 0.038, ${{r_0 {\rm \omega} } \over c}=75$, d = 50 and a0 = 0.1. For the sinusoidal profile modulation index α2 = 0.9 is used, and n00 is 0.02 times the critical density. (b) The variation of beam width parameter f with ξ for rectangular and sinusoidal density profiles based on analytical and numerical models. The parameters are ωp2/ω2 = 0.038, ${{r_0 {\rm \omega} } \over c}=75$, d = 50 and a0 = 0.4. For the sinusoidal profile modulation index α2 = 0.9 is used, and n00 is 0.02 times the critical density.

Figure 2

Fig. 3. (Color online) Critical power at normalized laser amplitude a0 = 0.18 –0.19, α1 = 0.02, α2 = 0.9, d = 50.

Figure 3

Fig. 4. (Color online) Variation of f with ξ for normalized laser amplitude a0 = 0.249 – 0.2515, where the critical power can be obtained at a0 = 0.25, α1 = 0.01, α2 = 0.2 and d = 50.

Figure 4

Fig. 5. (Color online) Comparison of beam width parameter at normalized laser amplitude a0 = 0.249 – 0.5 at α1 = 0.01, α2 = 0.2, d = 50.

Figure 5

Fig. 6. (Color online) Variation of beam width parameter f with distance of propagation ξ, for parameters α1 = 0.02, α2 = 0.9, ${{r_0 {\rm \omega} } \over c}=75$, d = 50 and d = 80, a0 = 1.0.